相关概念
二叉搜索树(BST, 也称二叉排序树/二叉查找树)
平衡二叉树(BBT, 也称AVL树)
红黑树
B树(也称多路平衡查找树)
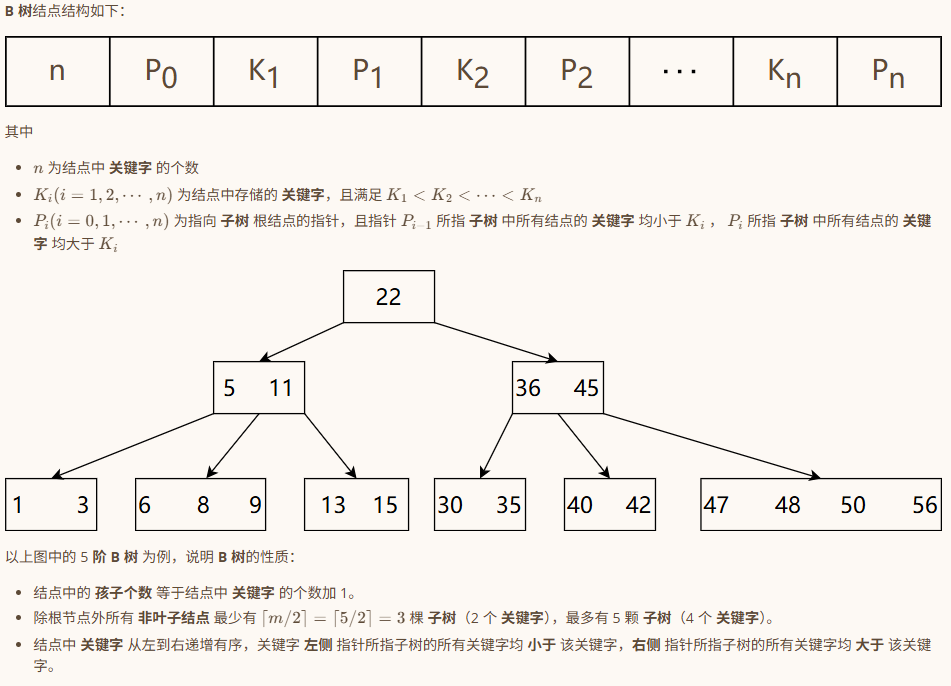
- 阶 (Order) B 树的阶定义了每个节点可以拥有的 最大子节点数。
- 平衡性B 树通过保持所有叶子节点在同一层,确保了树的平衡,从而保证了搜索效率。
- 关键字用来做大小比较、决定往哪棵子树走的"值"。
5阶B树示例计算
- 最多子树数:m = 5
- 最多关键字:m-1 = 4
- 非叶节点最少子树:⌈5/2⌉ = 3
- 非叶节点最少关键字:3-1 = 2
- 根结点最少子树:2
- 根结点最少子关键字:1
B树结构
B+树
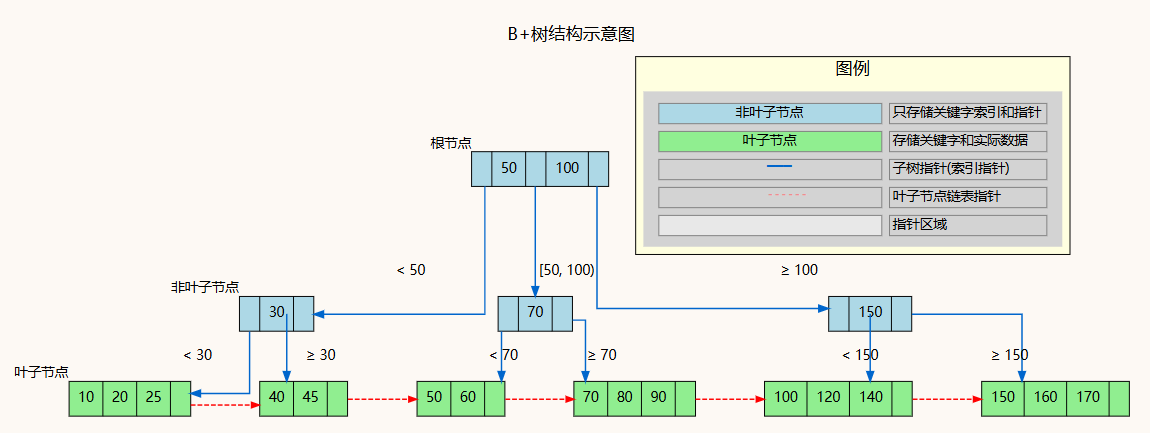
一颗 m 阶 B+ 树满足如下条件:
- 节点的容量限制
- 每个 非叶子节点 (分支节点)最多有 m 棵 子树。
- 除 根节点 外,每个 非叶子节点 至少有 ⌈ m/2 ⌉ 棵 子树。
- 关键字与子树的关系
- 在一个 非叶子节点 中,如果有 k 个关键字,那么它会有 k+1 棵 子树。
- 关键字起到分隔值域的作用,子树对应这些分隔区间。
- 数据存储位置
- 所有 数据记录 (或指向数据的指针)都存储在 叶子节点 中。
- 非叶子节点 只存储关键字,用于索引和导航,不直接存放数据。
- 叶子节点的顺序结构
- 所有 叶子节点 之间通过链表指针相连。
- 这种顺序结构可以支持高效的范围查询和顺序遍历。
B树和B+树的区别
- 查找 :
- B 树 :所有节点(包括内部节点)存储 KV 对,查找可能在内部节点结束。
- B+ 树 :只有 叶节点 存储 KV 对 ,查找必须到达 叶节点。
- 插入 :
- B 树 :所有节点存储 KV 对,分裂时中间键值对整体上移。
- B+ 树 :只有 叶节点 存储 KV 对 ,分裂时中间键复制到 父节点 (仅键,不带值),叶节点保留所有键。
- 删除 :
- B 树 :内部节点存储 KV 对,删除内部节点键需用后继/前驱替换,可能复杂。
- B+ 树 :删除只发生在 叶节点 ,内部节点键仅需调整(复制 叶节点 键),操作更简单。
| 特性 | B 树 | B+ 树 |
|---|---|---|
| 数据存储位置 | 关键字和数据存在于内部和 叶子节点 | 所有数据都存储在 叶子节点,内部节点只保存关键值和子节点的指针 |
| 叶子节点结构 | 叶子节点与内部节点类似,保存关键字和数据 | 所有 叶子节点 通过指针链接成链表 |
| 分支因子 | 由于同时保存数据和关键字,可能较小 | 通常较大,因为内部节点只保存关键字和指针 |
| 稳定性 | 关键字位置可能会频繁变动 | 数据位置相对稳定 |
| 应用场景 | 适用于小至中等规模的数据存储系统 | 更常见于大型数据库系统和文件系统 |
| 查找效率 | 在内部节点找到关键字后,查找即完成 | 查找必须遍历到 叶子节点,但由于通常高度较低,效率也很高 |
例题
- 在一株高度为 2 的 5 阶 B 树中,所含关键字的个数最少是()
答: 5