深度学习入门（三）——优化算法与实战技巧

---

一、前言：为什么我们需要"优化算法"？

在前两篇文章中，我们已经了解了深度学习的基本结构：

神经元、层、前向传播，以及通过链式法则实现的反向传播。理论上，只要我们能计算出梯度，就能通过不断调整权重，让模型逼近最优解。

但问题在于：

梯度只是方向，不是道路。

在真实的神经网络中，参数成千上万，甚至上亿。损失函数是一个极其复杂的高维空间，里面充满了局部极小值、鞍点、平原区（Plateau） 。

如果你只是用最朴素的梯度下降法（Gradient Descent），那你会发现模型要么收敛极慢，要么直接震荡，要么陷入局部极小值出不来。

于是，人们开始研究各种"优化算法"------它们不是在改动神经网络的本质，而是在改变梯度如何被利用。

我们这篇文章的目标就是搞清楚：

1. 梯度下降为什么难用？

2. 各种改进算法（SGD、Momentum、Adam 等）究竟改了什么？

3. 实际训练中，我们应该怎么选择优化器、怎么调整超参数？

---

二、从梯度下降出发

让我们先从最基础的**Batch Gradient Descent（批量梯度下降）**说起。

假设我们有一个损失函数 L(w)L(w)L(w)，它关于权重 www 可导。

我们希望找到一个 w∗w^*w∗ 使得 L(w∗)L(w^*)L(w∗) 最小。

基本更新规则如下：

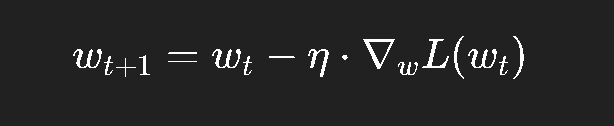
其中：

• η\etaη 称为 学习率 (learning rate)；

• ∇wL(wt)\nabla_w L(w_t)∇w​L(wt​) 是损失函数在当前点的梯度；

• 更新方向为梯度的反方向。

这就是最核心的思想：我们让权重往能最快降低损失的方向移动一点点。

但这个公式有三个致命问题：

1. 需要整个数据集的梯度

   每一次更新都要计算所有样本的梯度，计算量巨大。

2. 学习率难以选择

   太大了会震荡甚至发散，太小了又收敛太慢。

3. 复杂地形中容易迷路

   损失函数像一座山，有峡谷、有平原，有陡坡；光靠梯度就像盲人摸索，方向经常不靠谱。

于是我们引出了第一种改进------随机梯度下降法（SGD）。

---

三、随机梯度下降（SGD）：小步快跑的策略

**随机梯度下降（Stochastic Gradient Descent）**的核心思想是：

不必每次都用整个训练集，只用一小部分样本（mini-batch）近似估计梯度。

更新公式：

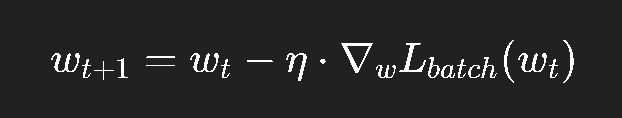
好处：

• 每次更新更快；

• 梯度中带有噪声，可以"跳出"局部最小值；

• 训练可以边走边学，不必等完整一轮。

缺点：

• 梯度噪声太大，会导致收敛轨迹抖动；

• 在鞍点附近容易来回晃动，甚至陷在平原地带。

举个直观例子：

假设你在山谷中骑自行车下山，批量梯度下降是"用地图规划最优路线"，但耗时太久；SGD 就像是"边滑边观察地形"，虽快，但方向不稳定，经常走几步又回头。

所以我们需要想办法让它"稳定一点"，这就引出了动量（Momentum）。

---

四、Momentum：惯性让梯度更聪明

动量算法的灵感来自物理世界。

我们知道，一个物体如果有质量 mmm，受到重力后会不断加速。即使地形有小的起伏，物体的惯性也会让它顺势滑过。

在优化中，SGD 每一步都是完全独立的，而 Momentum 引入了"惯性"，让梯度的历史方向也参与决策。

其更新规则：

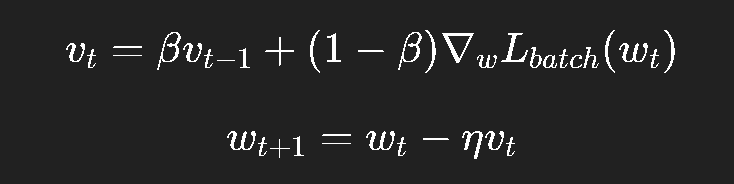
这里：

• vtv_tvt​ 是速度；

• β∈[0,1)\beta \in [0, 1)β∈[0,1) 是动量系数（通常取 0.9）；

• 它让梯度的平均方向主导更新。

直觉上：

• 如果梯度一直往同一方向，速度会越来越快；

• 如果梯度方向经常反转，速度会互相抵消，从而平滑抖动。

这就让参数更新更加平滑、效率更高。

伪代码如下：

v = 0
for each batch:
    grad = compute_gradient(L, w)
    v = beta * v + (1 - beta) * grad
    w = w - lr * v

Momentum 可以看作是 SGD 的"加速版"。

它不改变最终收敛点，但能显著加快收敛速度、减少震荡。

---

五、Nesterov 动量（NAG）：提前预判未来的加速版

Nesterov Momentum（NAG）是对 Momentum 的进一步优化。

普通 Momentum 是"到点再修正"；NAG 是"先预判再修正"。

更新逻辑如下：

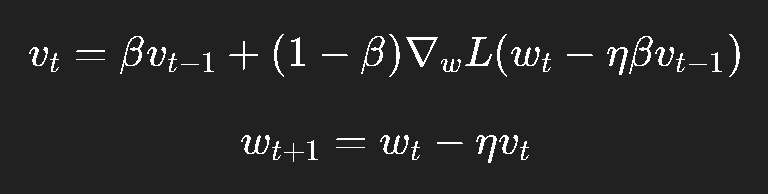
解释一下：

• 我们先假设沿着动量方向走一步；

• 再计算"预判位置"的梯度；

• 这样能更快修正方向，避免走过头。

这就像开车转弯时提前打方向，而不是撞到弯道才反应。

实践中，NAG 比普通 Momentum 在收敛初期表现更快、更稳，因此被广泛应用于如 RNN、CNN 的训练中。

---

六、学习率的艺术：η 并非越小越好

学习率 η\etaη 是深度学习中最敏感的超参数之一。

它决定了更新步伐的大小，也决定了能否找到最优解。

太小 → 训练像蜗牛一样；

太大 → 一不小心就"飞出山谷"。

于是人们又提出了自适应学习率（Adaptive Learning Rate）。

其核心思想是：

不同参数的重要性不同，更新幅度也该不同。

这类算法包括 AdaGrad、RMSProp、Adam 等。

---

七、AdaGrad：学会"少动一点"的自适应方法

AdaGrad 的思想非常简单：

如果某个参数更新次数多了，说明它已经比较稳定，就该让它动得更慢。

更新规则如下：

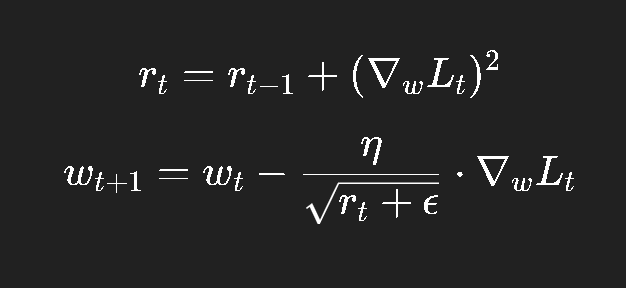
其中：

• rtr_trt​ 记录了每个参数梯度的平方和；

• 分母中的 rt\sqrt{r_t}rt​​ 会让频繁更新的参数步伐越来越小。

直觉上，这就像"踩刹车"：

• 梯度变化大的参数更新得慢；

• 梯度稳定的参数更新得快。

优点：

• 对稀疏特征特别有效（如 NLP 中的词向量训练）。

缺点：

• rtr_trt​ 会持续累加，导致学习率单调下降，最终几乎停止更新。

于是 RMSProp 诞生了。

---

八、RMSProp：让 AdaGrad 不再"刹过头"

RMSProp（Root Mean Square Propagation）由 Hinton 提出。

它保留了 AdaGrad 的思想，但不再无限累加梯度平方，而是用指数滑动平均：

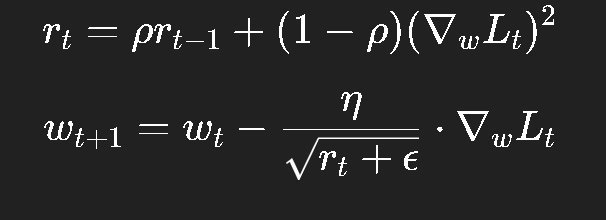
• 其中 ρ\rhoρ 通常取 0.9；

• 这样旧的梯度影响会随时间衰减；

• 学习率保持动态平衡。

它的效果非常稳定，是目前 RNN、LSTM 等结构中非常常用的优化器之一。

---

九、Adam：现代深度学习的默认选择

Adam（Adaptive Moment Estimation）几乎是当代深度学习的"默认优化器"。

它融合了 Momentum 和 RMSProp 的优点。

核心思想：

• 一阶矩：记录平均梯度（动量）；

• 二阶矩：记录平均平方梯度（自适应学习率）；

• 并加上偏差修正（bias correction）。

公式如下：

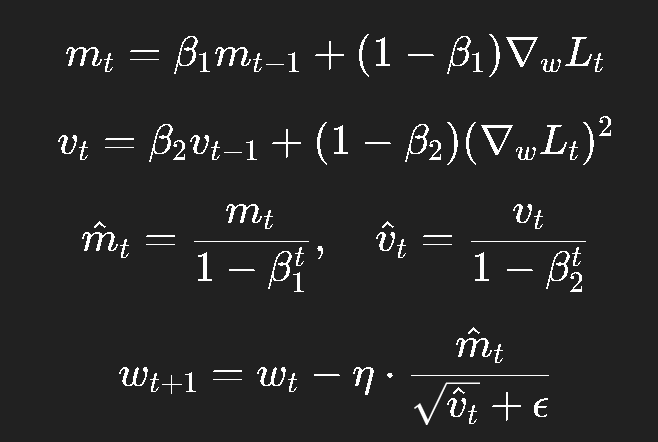
典型参数：

• β1=0.9,β2=0.999,ϵ=10−8\beta_1 = 0.9, \beta_2 = 0.999, \epsilon = 10^{-8}β1​=0.9,β2​=0.999,ϵ=10−8

伪代码：

m, v = 0, 0
for each batch:
    grad = compute_gradient(L, w)
    m = beta1 * m + (1 - beta1) * grad
    v = beta2 * v + (1 - beta2) * grad**2
    m_hat = m / (1 - beta1**t)
    v_hat = v / (1 - beta2**t)
    w = w - lr * m_hat / (sqrt(v_hat) + eps)

Adam 在收敛速度、稳定性、超参数敏感度上几乎全面优于 SGD。

但它也有潜在缺点：过度自适应可能导致最终解偏离全局最优。

因此在大模型训练中，也常使用 AdamW（带权重衰减的 Adam）。

---

十、实践经验与调参建议

理论我们讲了很多，实际训练时更重要的是经验与策略。

1. 学习率的设定与调整

• 初始学习率建议从 1e−31e^{-3}1e−3 或 1e−41e^{-4}1e−4 开始；

• 若损失在初期震荡或不降，可减半；

• 若损失下降太慢，可适当增大；

• 建议配合 学习率调度（Scheduler）：

  • Step Decay：每隔固定 epoch 降低学习率；

  • Cosine Annealing：模拟退火式衰减；

  • Warmup：初期先慢后快，防止梯度爆炸。

2. Batch 大小的选择

• 小 batch：收敛快但不稳定；

• 大 batch：稳定但可能陷入局部最小值；

• 通常取 32、64、128 等，视显存而定。

3. 正则化与防过拟合

• L2 权重衰减；

• Dropout；

• 数据增强；

• Early stopping。

4. 梯度裁剪（Gradient Clipping）

• 在 RNN、Transformer 等模型中防止梯度爆炸；

• 例如限制梯度模长不超过某阈值（如 5.0）。

5. 实战中优化器选择

场景	推荐优化器
传统小模型	SGD + Momentum
深度 CNN	Adam / AdamW
NLP Transformer	AdamW + Warmup
稀疏特征（词向量）	AdaGrad / FTRL

---

十一、结语：从算法到感觉

理解优化算法的过程，其实就是从"数学"走向"直觉"的过程。

它们的目标从未改变：让神经网络在复杂地形中更聪明地前进。

SGD 是探索者；

Momentum 是惯性的加速者；

RMSProp 是调速的工匠；

Adam 是现代化的自动驾驶系统。

但真正的工程师不会迷信算法，而是根据任务、数据、硬件、时间，选择最合适的工具。

深度学习不是单纯的数学游戏，它是一场与复杂性抗衡的修行。

---

下一篇预告：

深度学习入门（四）------常见模块与工程问题：

从激活函数到 BatchNorm，从 Dropout 到 Attention，我们将进入"现代神经网络工程"的领域。