简单来说,矩阵分块乘法,对 "怎么分" 是有讲究的,主要两个约束:
1.分块后要保证整体可乘(分后的小矩阵看作单个元素,包含这些小矩阵的大矩阵得是课程的,即 A x B,A 的列数要等于 B 的行数)
2.分块后,每个小矩阵之间都得是可乘的。
满足这两者,基本就能做计算。
具体看下面的图片,包含多种不同分法:



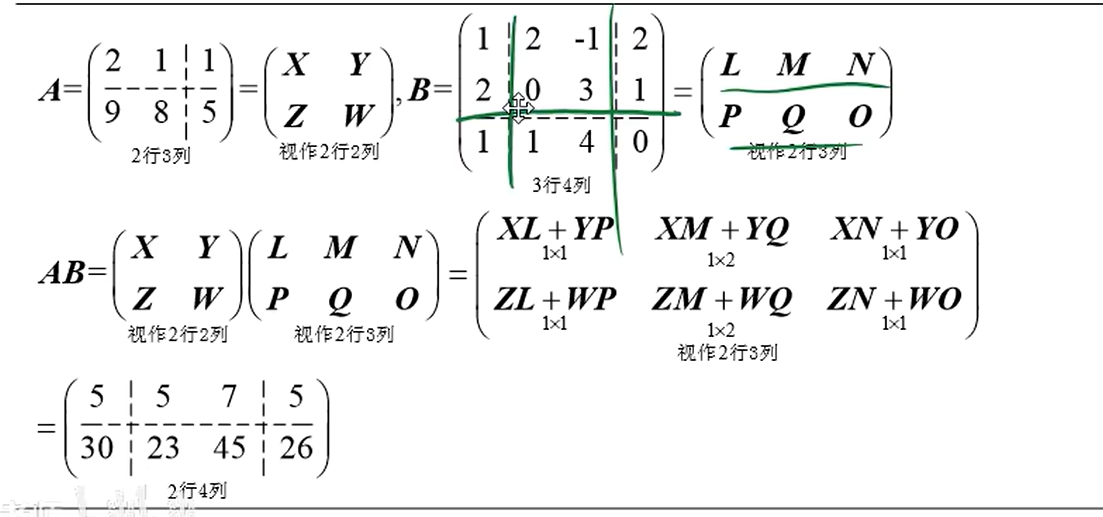
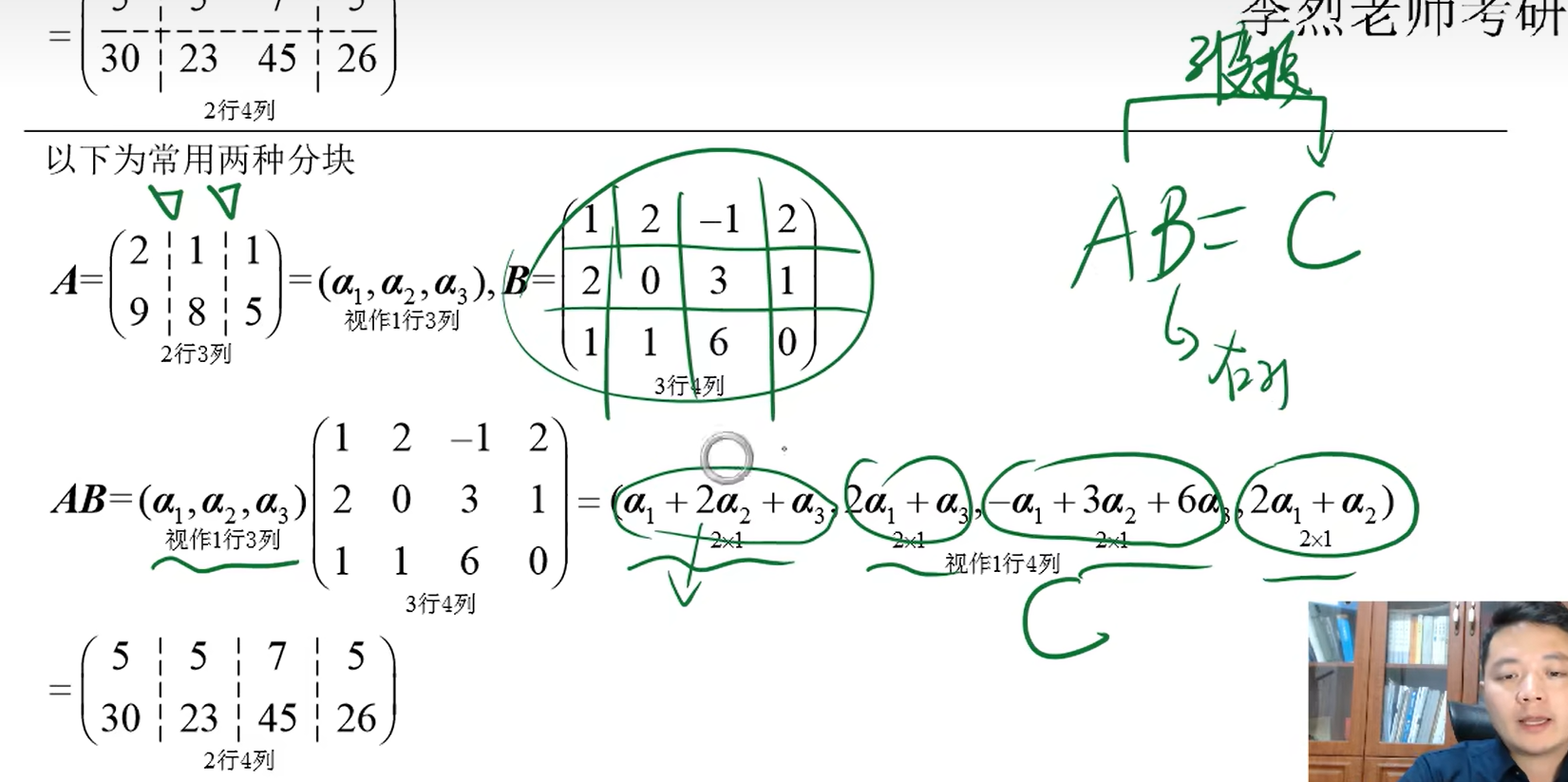
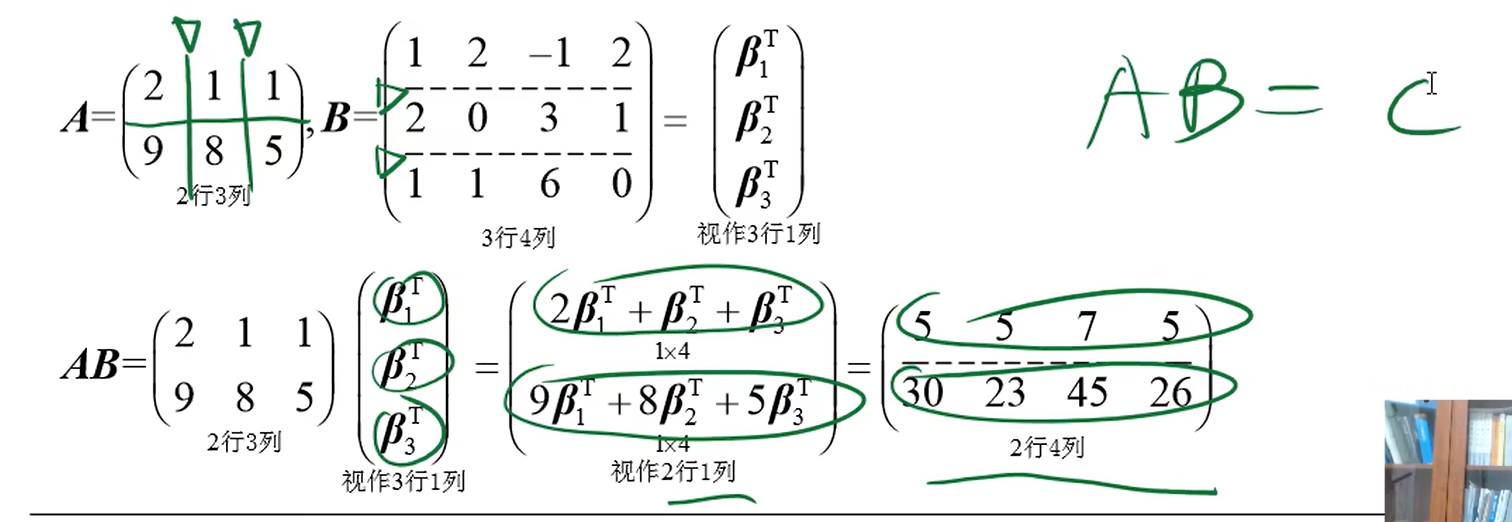
分块转置两个步骤:
1.整体转置
2.部分转置
具体看下面的图片:

简单来说,矩阵分块乘法,对 "怎么分" 是有讲究的,主要两个约束:
1.分块后要保证整体可乘(分后的小矩阵看作单个元素,包含这些小矩阵的大矩阵得是课程的,即 A x B,A 的列数要等于 B 的行数)
2.分块后,每个小矩阵之间都得是可乘的。
满足这两者,基本就能做计算。
具体看下面的图片,包含多种不同分法:






分块转置两个步骤:
1.整体转置
2.部分转置
具体看下面的图片:
