矩阵李群与李代数的定义
前言
矩阵李群的李代数的定义有两个,这两者的等价性问题挺有意思(搞清楚这两者的等价性,对搞清楚李代数的几何意义有很大帮助),所以写这一篇博客来记录。
本博客阅读预备知识: 已经知道基本的矩阵李群和李代数概念。
矩阵李群 的定义:矩阵李群 G G G是 G L ( n , C ) GL(n,\mathbb{C}) GL(n,C)的一个闭子群。
从定义来看,矩阵李群 G G G满足的条件 1. G G G是数域 C \mathbb{C} C上的n阶方阵的子集,2. G G G是一个群,3. 闭(即 G G G上的收敛序列的极限 G ∗ G^{*} G∗只要可逆,则 G ∗ ∈ G G^{*} \in G G∗∈G)。
矩阵李群的李代数 的定义: g = { X ∈ G L ( n , C ) ∣ e t X ∈ G } \mathfrak{g} = \{X \in GL(n, \mathbb{C}) | e^{tX} \in G\} g={X∈GL(n,C)∣etX∈G}。
从定义来看,矩阵李群的李代数 g \mathfrak{g} g满足的条件 1. g \mathfrak{g} g是 G L ( n ; C ) GL(n;\mathbb{C}) GL(n;C)的子集,2. 若 X ∈ g X \in \mathfrak{g} X∈g,则要求轨迹 e t X e^{tX} etX在流形 G G G上, t ∈ R t \in \mathbb{R} t∈R。(容易证明 { e t X ∣ t ∈ R } \{e^{tX}| t \in \mathbb{R} \} {etX∣t∈R}是 G G G的一个子群,且当 t = 0 t=0 t=0时, e t X = I e^{tX}=I etX=I)
讨论: 但从上述这个矩阵李群的李代数定义来看,似乎并不直观,我们不禁要问,为什么要定义这么奇怪的东西?李代数的几何意义是什么?
如Fig. 1所示,在 R 3 \mathbb{R}^{3} R3中的二维流形 S S S上有一个点 I I I,过点 I I I的任意光滑曲线记作 γ ( t ) \gamma(t) γ(t),且 γ ( 0 ) = I \gamma(0)=I γ(0)=I。这里的二维流形 S S S视作矩阵李群 流形,过点 I I I的任意光滑曲线 γ ( t ) \gamma(t) γ(t)的导数 d γ ( t ) d t ∣ t = 0 \frac{d\gamma(t)}{dt}|_{t=0} dtdγ(t)∣t=0都属于这个矩阵李群的李代数 g \mathfrak{g} g。这就是说,矩阵李群在点 I I I处的切空间 (所有切向量 )都属于李代数 g \mathfrak{g} g。
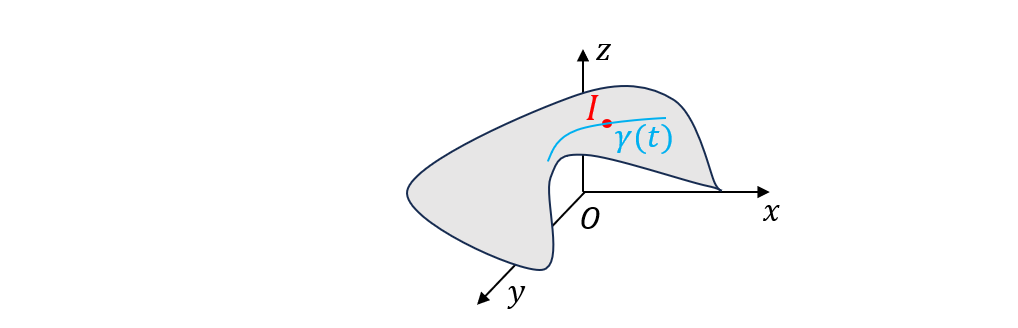
Fig. 1 R 3 \mathbb{R}^{3} R3中的二维流形
我们定义集合 T I G T_I G TIG,
T I G = { γ ′ ( 0 ) ∣ γ ( t ) ∈ G 且 γ ( 0 ) = I } T_I G = \{\gamma'(0) | \gamma(t) \in G且\gamma(0)=I\} TIG={γ′(0)∣γ(t)∈G且γ(0)=I}
这里 T I G T_I G TIG表示矩阵李群 G G G上所有过点 I I I的光滑曲线 γ ( t ) \gamma(t) γ(t)在点 I I I处的导数,或者从几何的角度来说,就是流形 G G G在点 I I I处的切空间。
我们给出以下命题,
命题: 矩阵李群的李代数 g = T I G \mathfrak{g}=T_I G g=TIG。
证明:
Step 1: 先证 g ⊂ T I G \mathfrak{g} \subset T_I G g⊂TIG
设 X ∈ g X \in \mathfrak{g} X∈g,则 e t X ∈ G e^{tX} \in G etX∈G,且 e t X = I e^{tX}=I etX=I 当 t = 0 t=0 t=0。 e t X e^{tX} etX是光滑的(把 e t X e^{tX} etX用级数表示,可以发现任意阶可导), d e t X d t ∣ t = 0 = X \frac{de^{tX}}{dt}|_{t=0} = X dtdetX∣t=0=X。所以 X ∈ T I G X \in T_I G X∈TIG。
Step 2: 再证 T I G ⊂ g T_I G \subset \mathfrak{g} TIG⊂g
设 X ∈ T I G X \in T_I G X∈TIG,即 ∃ γ ( t ) ∈ G \exists \gamma(t) \in G ∃γ(t)∈G, t ∈ R t \in \mathbb{R} t∈R,其中 γ ( 0 ) = I \gamma(0) = I γ(0)=I且 γ ′ ( 0 ) = X \gamma'(0) = X γ′(0)=X。
任取 t ∈ R t \in \mathbb{R} t∈R,因为 t n ∈ R \frac{t}{n} \in \mathbb{R} nt∈R, n ∈ N + n\in \mathbb{N}^{+} n∈N+,所以 γ ( t n ) ∈ G \gamma(\frac{t}{n}) \in G γ(nt)∈G。因为 G G G是群,所以 ( γ ( t n ) ) n ∈ G (\gamma(\frac{t}{n}))^{n} \in G (γ(nt))n∈G,对 ∀ n ∈ N + \forall n\in \mathbb{N}^{+} ∀n∈N+。
因为 γ ( t ) \gamma(t) γ(t)是光滑的,且 γ ′ ( 0 ) = X \gamma'(0) = X γ′(0)=X,所以 γ ( t n ) = I + t n X + o ( t n ) \gamma(\frac{t}{n}) = I + \frac{t}{n}X + o(\frac{t}{n}) γ(nt)=I+ntX+o(nt),当 n n n充分大。
lim n → ∞ ( γ ( t n ) ) n = lim n → ∞ ( I + t n X + o ( t n ) ) n = lim n → ∞ ( I + t n X ) n = e t X \begin{align} & \lim_{n\to \infty}(\gamma(\frac{t}{n}))^{n} \tag{1}\\ &= \lim_{n\to \infty}(I+\frac{t}{n}X+o(\frac{t}{n}))^{n} \tag{2}\\ &= \lim_{n\to \infty}(I + \frac{t}{n}X)^{n} \tag{3}\\ &= e^{tX} \tag{4} \end{align} n→∞lim(γ(nt))n=n→∞lim(I+ntX+o(nt))n=n→∞lim(I+ntX)n=etX(1)(2)(3)(4)
因为 G G G是矩阵李群,所以极限 e t X ∈ G e^{tX}\in G etX∈G。由于 t t t的任意性,所以 e t X ∈ G e^{tX}\in G etX∈G, ∀ t ∈ R \forall t \in \mathbb{R} ∀t∈R。所以, X ∈ g X \in \mathfrak{g} X∈g。
综上, g = T I G \mathfrak{g} = T_I G g=TIG。证毕。
注: 上述的Step 2 中的证明中,(2)式到(3)式,(3)式到(4)式似乎并不显然易见。我们在补充部分中继续给出(2)到(3)的证明和(3)到(4)的证明。
重要命题: 矩阵李群 G G G的李代数 g \mathfrak{g} g是一个实线性空间。
证明:设 X ∈ g X \in \mathfrak{g} X∈g,即 e t X ∈ G e^{tX} \in G etX∈G,对 ∀ t ∈ R \forall t\in \mathbb{R} ∀t∈R。
对 ∀ α ∈ R \forall \alpha \in \mathbb{R} ∀α∈R,因为 e t α X ∈ G e^{t\alpha X}\in G etαX∈G,所以 α X ∈ g \alpha X \in \mathfrak{g} αX∈g。
设 X , Y ∈ g X,Y \in \mathfrak{g} X,Y∈g,即 e t X , e t Y ∈ G e^{tX}, e^{tY} \in G etX,etY∈G,对 ∀ t ∈ R \forall t \in \mathbb{R} ∀t∈R。
e t ( X + Y ) = lim m → ∞ ( e t X m e t Y m ) m ∈ G e^{t(X+Y)}=\lim_{m\to \infty}(e^{\frac{tX}{m}}e^{\frac{tY}{m}})^{m}\in G et(X+Y)=limm→∞(emtXemtY)m∈G。(这个证明基于 e X + Y = lim m → ∞ ( e X m e Y m ) m e^{X+Y}=\lim_{m\to \infty}(e^{\frac{X}{m}}e^{\frac{Y}{m}})^{m} eX+Y=limm→∞(emXemY)m这个等式,这个等式我们不证明,如果有兴趣,可以自行网上搜索证明)
综上, g \mathfrak{g} g是一个实线性空间。
矩阵李群和其李代数的例子
例子:求矩阵李群 S O ( 3 ) SO(3) SO(3)的李代数
设 X ∈ g X \in \mathfrak{g} X∈g,则 e t X ∈ S O ( 3 ) e^{tX} \in SO(3) etX∈SO(3),对 ∀ t ∈ R \forall t\in \mathbb{R} ∀t∈R。
因为 e t X ∈ S O ( 3 ) e^{tX} \in SO(3) etX∈SO(3),所以 e t X ( e t X ) T = I e^{tX}(e^{tX})^{T}=I etX(etX)T=I,对 ∀ t ∈ R \forall t\in \mathbb{R} ∀t∈R。
e t X e t X T = I e^{tX}e^{tX^{T}}=I etXetXT=I,因为 X X T = X T X = I XX^{T}=X^{T}X=I XXT=XTX=I(满足可交换,即 e A e B = e A + B e^{A}e^{B}=e^{A+B} eAeB=eA+B,当 A B = B A AB=BA AB=BA时。证明见补充部分 ), 所以 I = e t X e t X T = e t X + t X T = e t ( X + X T ) I=e^{tX}e^{tX^{T}}=e^{tX+tX^{T}}=e^{t(X+X^{T})} I=etXetXT=etX+tXT=et(X+XT),对 ∀ t ∈ R \forall t\in \mathbb{R} ∀t∈R。
因为 d e t ( X + X T ) d t ∣ t = 0 = X + X T \frac{de^{t(X+X^T)}}{dt}|{t=0}=X+X^{T} dtdet(X+XT)∣t=0=X+XT,又因为 d e t ( X + X T ) d t ∣ t = 0 = d I d t ∣ t = 0 = O \frac{de^{t(X+X^T)}}{dt}|{t=0} = \frac{dI}{dt}|_{t=0}=O dtdet(X+XT)∣t=0=dtdI∣t=0=O。所以 X + X T = O X+X^{T}=O X+XT=O。
即 X X X是一个反对称矩阵,我们断言 X X X是一个实矩阵(因为根据李代数的等价定义, X = d γ ( t ) d t ∣ t = 0 X=\frac{d\gamma(t)}{dt}|_{t=0} X=dtdγ(t)∣t=0, γ ( t ) \gamma(t) γ(t)是 S O ( 3 ) SO(3) SO(3)上的光滑曲线, γ ( t ) \gamma(t) γ(t)是实数矩阵,对 ∀ t ∈ R \forall t\in \mathbb{R} ∀t∈R。所以 γ ( t ) \gamma(t) γ(t)的导数也一定是实矩阵)。
因为 X X X是一个实的反对称矩阵,所以
X = ( 0 − c b c 0 − a − b a 0 ) X=\begin{pmatrix} 0 & -c & b \\ c & 0 & -a\\ -b& a & 0 \end{pmatrix} X= 0c−b−c0ab−a0
可以看到李代数 g \mathfrak{g} g是由
( 0 − 1 0 1 0 0 0 0 0 ) ( 0 0 1 0 0 0 − 1 0 0 ) ( 0 0 0 0 0 − 1 0 1 0 ) \begin{pmatrix} 0 & -1 & 0 \\ 1 & 0 & 0\\ 0& 0 & 0 \end{pmatrix} \quad \begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0\\ -1& 0 & 0 \end{pmatrix} \quad \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & -1\\ 0& 1 & 0 \end{pmatrix} 010−100000 00−1000100 0000010−10
这三个基张成的线性空间。
S O ( 3 ) SO(3) SO(3)作为 R 9 \mathbb{R}^9 R9空间中的流形,李代数 g \mathfrak{g} g的三个基相当于是3个线性无关的切向量的方向,它们张成的线性空间是 I I I点的切空间。(可以类比Fig. 1中的 I I I点处的切平面,其实就是一个2维的线性空间,可以由 I I I点处的两个线性无关的方向向量来张成。)
补充部分
求证: 若 A B = B A AB=BA AB=BA,则 e A e B = e A + B e^{A}e^{B}=e^{A+B} eAeB=eA+B
证明: e A e B = ∑ k = 0 ∞ A k k ! ∑ l = 0 ∞ B l l ! = ∑ k = 0 ∞ ∑ l = 0 ∞ A k k ! B l l ! (I) e^{A}e^{B}=\sum^{\infty}{k=0}\frac{A^{k}}{k!}\sum^{\infty}{l=0}\frac{B^{l}}{l!}=\sum^{\infty}{k=0}\sum^{\infty}{l=0}\frac{A^{k}}{k!}\frac{B^{l}}{l!} \tag{I} eAeB=k=0∑∞k!Akl=0∑∞l!Bl=k=0∑∞l=0∑∞k!Akl!Bl(I)
e A + B = ∑ n = 0 ∞ ( A + B ) n n ! (II) e^{A+B}=\sum^{\infty}{n=0}\frac{(A+B)^n}{n!} \tag{II} eA+B=n=0∑∞n!(A+B)n(II)
(I) \text{(I)} (I)式中乘开后的每一项都是 A k B l k ! l ! \frac{A^{k}B^{l}}{k!l!} k!l!AkBl的形式。 (II) \text{(II)} (II)式用二项式展开后,包含 A k B l A^{k}B^{l} AkBl的项是 ( A + B ) n n ! \frac{(A+B)^n}{n!} n!(A+B)n中的 C k + l k ( k + l ) ! A k B l \frac{C^{k}{k+l}}{(k+l)!}A^{k}B^{l} (k+l)!Ck+lkAkBl。因为 C k + l k ( k + l ) ! A k B l = A k B l k ! l ! \frac{C^{k}_{k+l}}{(k+l)!}A^{k}B^{l}=\frac{A^{k}B^{l}}{k!l!} (k+l)!Ck+lkAkBl=k!l!AkBl,所以 (I) \text{(I)} (I)式 等于 (II) \text{(II)} (II)式。证毕。
求证: lim n → ∞ ( I + t n X + o ( t n ) ) n = lim n → ∞ ( I + t n X ) n \lim_{n\to \infty}(I+\frac{t}{n}X+o(\frac{t}{n}))^{n} = \lim_{n\to \infty}(I + \frac{t}{n}X)^{n} limn→∞(I+ntX+o(nt))n=limn→∞(I+ntX)n
证明:本质上这个问题等价于" lim n → ∞ ( 1 + x n + ϵ n ) n = lim n → ∞ ( 1 + x n ) n \lim_{n\to \infty}(1+\frac{x}{n}+\epsilon_{n})^{n}=\lim_{n\to \infty}(1+\frac{x}{n})^{n} limn→∞(1+nx+ϵn)n=limn→∞(1+nx)n, ϵ n = o ( 1 n ) \epsilon_{n}=o(\frac{1}{n}) ϵn=o(n1)"
我们证明等价命题,
记 A n = ( 1 + x n + ϵ n ) n A_n = (1+\frac{x}{n}+\epsilon_{n})^{n} An=(1+nx+ϵn)n, B n = ( 1 + x n ) n B_n = (1+\frac{x}{n})^{n} Bn=(1+nx)n
由拉格朗日中值定理知,
ln ( A n B n ) = n ( ln ( 1 + x n + ϵ n ) − ln ( 1 + x n ) ) = n f ′ ( θ ) ϵ n \ln(\frac{A_n}{B_n})=n(\ln(1+\frac{x}{n}+\epsilon_{n})-\ln(1+\frac{x}{n}))=nf'(\theta)\epsilon_{n} ln(BnAn)=n(ln(1+nx+ϵn)−ln(1+nx))=nf′(θ)ϵn,其中 θ ∈ ( 1 + x n , 1 + x n + ϵ n ) \theta \in (1+\frac{x}{n}, 1+\frac{x}{n}+\epsilon_{n}) θ∈(1+nx,1+nx+ϵn), f ′ ( θ ) = d ln ( 1 + x ) d x ∣ x = θ = 1 θ f'(\theta)=\frac{d\ln(1+x)}{dx}|{x=\theta}=\frac{1}{\theta} f′(θ)=dxdln(1+x)∣x=θ=θ1。
lim n → ∞ ln ( A n B n ) = lim n → ∞ n f ′ ( θ ) ϵ n = 0 \lim{n\to\infty}\ln(\frac{A_n}{B_n})=\lim_{n\to\infty}nf'(\theta)\epsilon_n=0 limn→∞ln(BnAn)=limn→∞nf′(θ)ϵn=0,因为 lim n → ∞ n ϵ n = 0 \lim_{n\to\infty}n\epsilon_n=0 limn→∞nϵn=0, lim n → ∞ f ′ ( θ ) = 1 \lim_{n\to\infty}f'(\theta)=1 limn→∞f′(θ)=1。
则 lim n → ∞ A n B n = 1 \lim_{n\to\infty}\frac{A_n}{B_n}=1 limn→∞BnAn=1。证毕。
求证: lim n → ∞ ( I + t n X ) n = e t X \lim_{n\to \infty}(I + \frac{t}{n}X)^{n} = e^{tX} limn→∞(I+ntX)n=etX
证明:由于上式左边部分的展开和 ( 1 + x n ) n (1+\frac{x}{n})^{n} (1+nx)n的展开一样(由于 I I I和 X X X可交换),本质上这个问题等价于" lim n → ∞ ( 1 + x n ) n = e x \lim_{n\to\infty}(1+\frac{x}{n})^{n}=e^{x} limn→∞(1+nx)n=ex" (这个命题我们非常熟悉,证明用到下述的Tannery定理 )
由二项式展开, ( 1 + x n ) n = ∑ k = 0 n C n k 1 n − k ( x n ) k = ∑ k = 0 n C n k ( x n ) k (1+\frac{x}{n})^{n}=\sum^{n}{k=0}C^{k}{n}1^{n-k}(\frac{x}{n})^{k}=\sum^{n}{k=0}C^{k}{n}(\frac{x}{n})^{k} (1+nx)n=∑k=0nCnk1n−k(nx)k=∑k=0nCnk(nx)k
记 a n , k = C n k ( x n ) k a_{n,k}=C^{k}_{n}(\frac{x}{n})^{k} an,k=Cnk(nx)k,代入Tannery定理 ,可以发现
1.对每一个固定的 k k k, lim n → ∞ a n , k = a k \lim_{n\to\infty}a_{n,k}=a_{k} limn→∞an,k=ak,其中 a k = lim n → ∞ n ( n − 1 ) ... ( n − k + 1 ) k ! ( x n ) k = x k k ! a_{k}=\lim_{n\to\infty}\frac{n(n-1)\dots(n-k+1)}{k!}(\frac{x}{n})^{k}=\frac{x^{k}}{k!} ak=limn→∞k!n(n−1)...(n−k+1)(nx)k=k!xk;
2.存在与 n n n无关的 M k ≥ 0 M_{k}\geq 0 Mk≥0,使 ∣ a n , k ∣ = ∣ C n k ( x n ) k ∣ = ∣ n ( n − 1 ) ... ( n − k + 1 ) k ! ( x n ) k ∣ ≤ ∣ x k k ! ∣ = M k |a_{n,k}| = |C^{k}{n}(\frac{x}{n})^{k}| = |\frac{n(n-1)\dots(n-k+1)}{k!}(\frac{x}{n})^{k}|\leq |\frac{x^k}{k!}| = M_k ∣an,k∣=∣Cnk(nx)k∣=∣k!n(n−1)...(n−k+1)(nx)k∣≤∣k!xk∣=Mk对所有的 n , k n,k n,k都成立,且 ∑ k = 0 ∞ M k = ∑ k = 0 ∞ ∣ x k k ! ∣ = e ∣ x ∣ < ∞ \sum^{\infty}{k=0}M_k = \sum^{\infty}_{k=0}|\frac{x^{k}}{k!}|=e^{|x|}<\infty ∑k=0∞Mk=∑k=0∞∣k!xk∣=e∣x∣<∞
则
lim n → ∞ ( 1 + x n ) n = lim n → ∞ ∑ k = 0 n C n k ( x n ) k = lim n → ∞ ∑ k = 0 n a n , k = ∑ k = 0 ∞ a k = ∑ k = 0 ∞ x k k ! = e x \lim_{n\to\infty}(1+\frac{x}{n})^{n} =\lim_{n\to\infty}\sum^{n}{k=0}C^{k}{n}(\frac{x}{n})^{k} = \lim_{n\to\infty}\sum^{n}{k=0}a{n,k} = \sum^{\infty}{k=0}a{k} = \sum^{\infty}_{k=0}\frac{x^k}{k!}=e^x n→∞lim(1+nx)n=n→∞limk=0∑nCnk(nx)k=n→∞limk=0∑nan,k=k=0∑∞ak=k=0∑∞k!xk=ex
证毕。
定理: (Tannery定理 三角数组版)
如Fig. 2所示,设 a n , k a_{n,k} an,k( n , k ∈ N n,k \in \mathbb{N} n,k∈N)满足:
1.对每个固定的 k k k, lim n → ∞ a n , k = a k \lim_{n\to\infty}a_{n,k}=a_{k} limn→∞an,k=ak;
2.存在与 n n n无关的 M k ≥ 0 M_{k}\geq 0 Mk≥0,使 ∣ a n , k ∣ ≤ M k |a_{n,k}| \leq M_{k} ∣an,k∣≤Mk对所有 n , k n,k n,k都成立,且 ∑ k = 0 ∞ M k < ∞ \sum^{\infty}{k=0}M{k}<\infty ∑k=0∞Mk<∞。
则
lim n → ∞ ∑ k = 0 n a n , k = ∑ k = 0 ∞ a k \lim_{n\to\infty}\sum^{n}{k=0}a{n,k}=\sum^{\infty}{k=0}a{k} n→∞limk=0∑nan,k=k=0∑∞ak
并且右端级数绝对收敛。
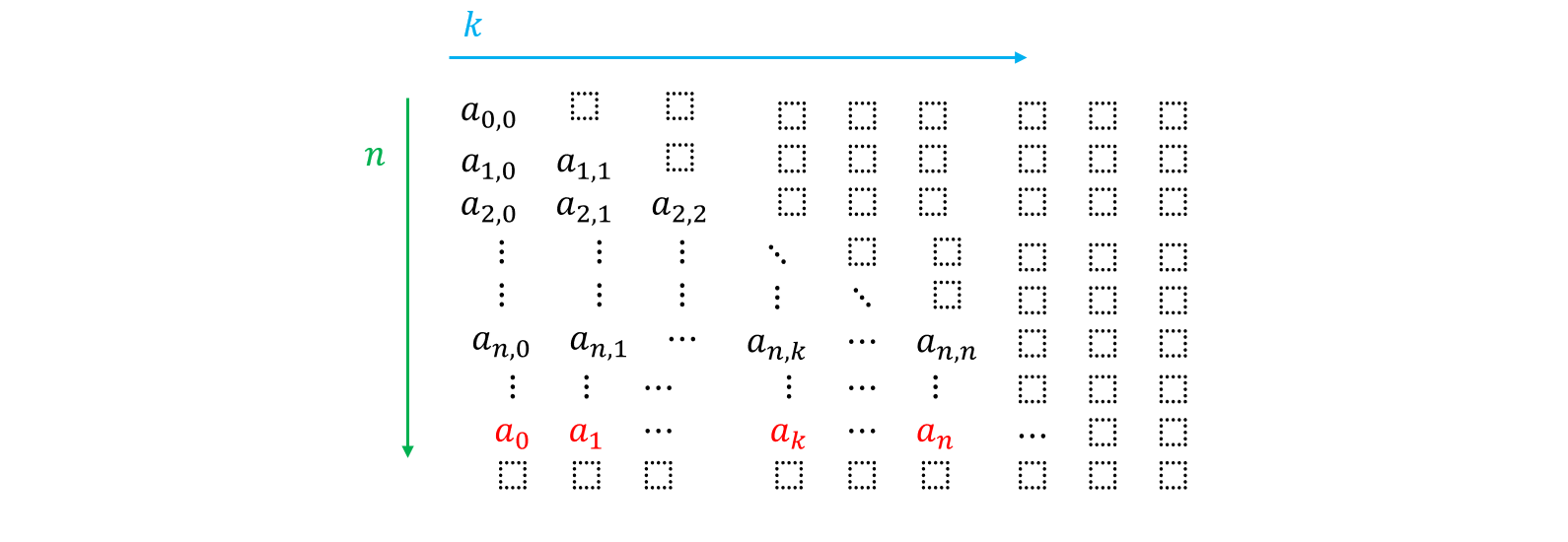
Fig. 2 三角数组
证明:
首先,对Fig. 2中的三角数组的右上角部分全赋值为0,即 a n , k = 0 a_{n,k}=0 an,k=0,当 k > n k>n k>n。
令
Δ n : = ∣ ∑ k = 0 n a n , k − ∑ k = 0 ∞ a k ∣ \Delta_{n} := |\sum^{n}{k=0}a{n,k}-\sum^{\infty}{k=0}a{k}| Δn:=∣k=0∑nan,k−k=0∑∞ak∣
对任意固定的 N ∈ N N \in \mathbb{N} N∈N,
Δ n = ∣ ∑ k = 0 N ( a n , k − a k ) + ∑ k = N + 1 n a n , k − ∑ k = N + 1 ∞ a k ∣ ≤ ∑ k = 0 N ∣ a n , k − a k ∣ ⏟ Section I + ∑ k = N + 1 n ∣ a n , k ∣ ⏟ Section II + ∑ k = N + 1 ∞ ∣ a k ∣ ⏟ Section III (*) \Delta_{n} = |\sum^{N}{k=0}(a{n,k}-a_{k})+\sum^{n}{k=N+1}a{n,k}-\sum^{\infty}{k=N+1}a{k}| \\ \leq \underbrace{\sum^{N}{k=0}|a{n,k}-a_{k}|}{\text{Section I}} + \underbrace{\sum^{n}{k=N+1}|a_{n,k}|}{\text{Section II}}+\underbrace{\sum^{\infty}{k=N+1}|a_{k}|}_{\text{Section III}} \tag{*} Δn=∣k=0∑N(an,k−ak)+k=N+1∑nan,k−k=N+1∑∞ak∣≤Section I k=0∑N∣an,k−ak∣+Section II k=N+1∑n∣an,k∣+Section III k=N+1∑∞∣ak∣(*)
对于 ( ∗ ) (*) (∗)式,分为三个部分,下面分别控制这三个部分的上界,
1.控制 Section III \text{Section III} Section III
因为对每个固定 k k k,有 lim n → ∞ a n , k = a k \lim_{n\to\infty}a_{n,k}=a_{k} limn→∞an,k=ak,且对 ∀ n , k \forall n,k ∀n,k, ∣ a n , k ∣ ≤ M k |a_{n,k}|\leq M_{k} ∣an,k∣≤Mk且 ∑ k = 0 ∞ M k < ∞ \sum^{\infty}{k=0}M{k}<\infty ∑k=0∞Mk<∞,所以 ∑ k = 0 ∞ ∣ a k ∣ ≤ ∑ n = 0 ∞ M k < ∞ \sum^{\infty}{k=0}|a{k}|\leq \sum^{\infty}{n=0}M{k}<\infty ∑k=0∞∣ak∣≤∑n=0∞Mk<∞。则给定 ϵ > 0 \epsilon>0 ϵ>0,存在 N 1 ∈ N + N_{1}\in \mathbb{N}^{+} N1∈N+,当 N > N 1 N>N_{1} N>N1时,使得
∑ k = N + 1 ∞ ∣ a k ∣ < ϵ 3 \sum^{\infty}{k=N+1}|a{k}|< \frac{\epsilon}{3} k=N+1∑∞∣ak∣<3ϵ
2.控制 Section II \text{Section II} Section II
Section II \text{Section II} Section II的求和中有两个变量 n n n和 k k k。因为对 ∀ n , k \forall n,k ∀n,k, ∣ a n , k ∣ < M k |a_{n,k}|<M_{k} ∣an,k∣<Mk,所以 ∑ k = N + 1 n ∣ a n , k ∣ ≤ ∑ k = N + 1 ∞ M k \sum^{n}{k=N+1}|a{n,k}| \leq \sum^{\infty}{k=N+1}M{k} ∑k=N+1n∣an,k∣≤∑k=N+1∞Mk(注意:这样就能保证 ∑ k = N + 1 n ∣ a n , k ∣ \sum^{n}{k=N+1}|a{n,k}| ∑k=N+1n∣an,k∣的上界只与 N N N有关,而与 n n n无关)。因为 ∑ k = 0 ∞ M k < ∞ \sum^{\infty}{k=0}M{k}<\infty ∑k=0∞Mk<∞,所以存在 N 2 ∈ N + N_{2} \in \mathbb{N}^{+} N2∈N+,当 N > N 2 N>N_{2} N>N2时,使得 ∑ k = N + 1 ∞ M k < ϵ 3 \sum^{\infty}{k=N+1}M{k}< \frac{\epsilon}{3} ∑k=N+1∞Mk<3ϵ。即有
∑ k = N + 1 n ∣ a n , k ∣ ≤ ∑ k = N + 1 ∞ M k < ϵ 3 \sum^{n}{k=N+1}|a{n,k}|\leq \sum^{\infty}{k=N+1}M{k}< \frac{\epsilon}{3} k=N+1∑n∣an,k∣≤k=N+1∑∞Mk<3ϵ
3.控制 Section I \text{Section I} Section I
取 N ′ = max ( N 1 , N 2 ) + 1 N' = \max(N_{1},N_{2})+1 N′=max(N1,N2)+1,令 N = N ′ N=N' N=N′,因为对于每个固定 k k k, lim n → ∞ a n , k = a k \lim_{n\to\infty} a_{n,k}=a_{k} limn→∞an,k=ak,所以存在充分大得 n ′ ∈ N + n'\in\mathbb{N}^{+} n′∈N+,对 k = 0 , 1 , . . . , N k=0,1,...,N k=0,1,...,N,有 ∣ a n ′ , k − a k ∣ < ϵ 3 ( N + 1 ) |a_{n',k}-a_{k}|<\frac{\epsilon}{3(N+1)} ∣an′,k−ak∣<3(N+1)ϵ。于是
∑ k = 0 N ∣ a n ′ , k − a k ∣ ≤ ( N + 1 ) ϵ 3 ( N + 1 ) = ϵ 3 \sum^{N}{k=0}|a{n',k}-a_{k}|\leq (N+1)\frac{\epsilon}{3(N+1)}=\frac{\epsilon}{3} k=0∑N∣an′,k−ak∣≤(N+1)3(N+1)ϵ=3ϵ
综上,
Δ n ′ = ∣ ∑ k = 0 N ′ ( a n ′ , k − a k ) + ∑ k = N ′ + 1 n ′ a n ′ , k − ∑ k = N ′ + 1 ∞ a k ∣ ≤ ∑ k = 0 N ′ ∣ a n ′ , k − a k ∣ ⏟ Section I + ∑ k = N ′ + 1 n ′ ∣ a n ′ , k ∣ ⏟ Section II + ∑ k = N ′ + 1 ∞ ∣ a k ∣ ⏟ Section III < ϵ 3 + ϵ 3 + ϵ 3 = ϵ \Delta_{n'} = |\sum^{N'}{k=0}(a{n',k}-a_{k})+\sum^{n'}{k=N'+1}a{n',k}-\sum^{\infty}{k=N'+1}a{k}| \\ \leq \underbrace{\sum^{N'}{k=0}|a{n',k}-a_{k}|}{\text{Section I}} + \underbrace{\sum^{n'}{k=N'+1}|a_{n',k}|}{\text{Section II}}+\underbrace{\sum^{\infty}{k=N'+1}|a_{k}|}_{\text{Section III}} < \frac{\epsilon}{3} + \frac{\epsilon}{3} + \frac{\epsilon}{3} = \epsilon Δn′=∣k=0∑N′(an′,k−ak)+k=N′+1∑n′an′,k−k=N′+1∑∞ak∣≤Section I k=0∑N′∣an′,k−ak∣+Section II k=N′+1∑n′∣an′,k∣+Section III k=N′+1∑∞∣ak∣<3ϵ+3ϵ+3ϵ=ϵ
即对 ∀ ϵ > 0 , ∃ n ′ ∈ N + , s . t . Δ n ′ < ϵ \forall \epsilon>0, \exists n'\in \mathbb{N}^{+}, s.t. \Delta_{n'}<\epsilon ∀ϵ>0,∃n′∈N+,s.t.Δn′<ϵ,所以 lim n → ∞ ∑ k = 0 n = ∑ k = 0 ∞ a k \lim_{n\to\infty}\sum^{n}{k=0}=\sum^{\infty}{k=0}a_{k} limn→∞∑k=0n=∑k=0∞ak。证毕。
写在最后
上述如有错误,恳请指正,谢谢。同时,欢迎讨论。