Large Scale Diffusion Distillation Via Score-Regularized Continuous-Time Consistency
摘要 (Abstract)
这篇论文的核心贡献是首次将连续时间一致性蒸馏 (continuous-time consistency distillation) 的方法成功扩展到大规模、应用级别的图像和视频扩散模型上。
- 背景与挑战 :
- 理论上,连续时间一致性模型 (sCM) 在加速学术级别的扩散模型方面表现出色。但由于雅可比向量积 (Jacobian-vector product, JVP) 的计算存在技术瓶颈,以及标准评估基准的局限性,sCM 在大规模图生文 (T2I) 和视频生成 (T2V) 任务上的应用前景并不明朗。
- 技术突破 :
- 基础设施: 作者开发了一个与并行计算兼容的 FlashAttention-2 JVP 内核,使得 sCM 能够训练超过100亿参数的模型和处理高维视频任务。
- 问题发现: 研究发现,sCM 在生成精细细节方面存在根本性的质量问题,作者将其归因于误差累积以及其前向散度 (forward-divergence) 目标的"模式覆盖 (mode-covering)"特性。
- 提出 rCM : 为了解决这个问题,论文提出了分数正则化的连续时间一致性模型 (score-regularized continuous-time consistency model, rCM)。该模型将分数蒸馏 (score distillation) 作为一种长跳跃正则化器 (long-skip regularizer)。这种方法通过引入"模式寻求 (mode-seeking)"的反向散度 (reverse divergence),有效提升了视觉质量,同时保持了生成的多样性。
- 实验与结果 :
- rCM 在高达 140 亿参数的大型模型 (Cosmos-Predict2, Wan2.1) 和长达 5 秒的视频上进行了验证。
- 结果显示,rCM 在质量指标上媲美甚至超越了当前最先进的蒸馏方法 DMD2,同时在多样性上表现出显著优势,并且无需复杂的 GAN 调优或大量超参数搜索。
- 蒸馏后的模型仅需 1 到 4 步就能生成高保真样本,将扩散模型的采样速度提升了 15 到 50 倍。

第1章: 引言 (Introduction)
本章首先介绍了扩散模型作为生成式人工智能基石的地位,指出了其虽然在质量、多样性和稳定性上优于 GAN 等模型,但存在推理速度慢的缺点。
- 加速方法 :
- 免训练加速: 通过专门的采样器(如 DPM-Solver)可以将采样步数减少到 10 步以上,但受限于数值求解器的离散化误差。
- 基于训练的蒸馏: 可以实现少步甚至单步生成,是更有效的加速途径。主要方法包括知识蒸馏、渐进式蒸馏、一致性蒸馏、分数蒸馏和对抗蒸馏等。
- 一致性模型 (CM) 的优势与 sCM 的提出 :
- 一致性模型(CMs)因其无需生成合成数据或进行 GAN 训练,同时能保持生成多样性,在图像基准上表现优异而备受关注。
- 随后提出的连续时间一致性模型 (sCM) 是一个理论上更优雅的扩展,它消除了离散化误差,使训练与特定采样器解耦,并无需启发式的退火计划。
- sCM 的局限性 :
- 规模化挑战: 尽管 sCM 在 ImageNet 上展示了扩展到 15 亿参数模型的能力,但现实应用中的大规模训练基础设施(如 BF16 精度、FlashAttention、上下文并行)会使其 JVP 计算变得复杂并引入数值错误。
- 评估局限: 先前的评估主要集中在弱条件的 ImageNet 基准上,使用 FID 作为指标,而 T2I 和 T2V 任务是强条件的,强调 FID 无法捕捉的细粒度属性(如文字渲染)。
- 本文贡献与 rCM 的核心思想 :
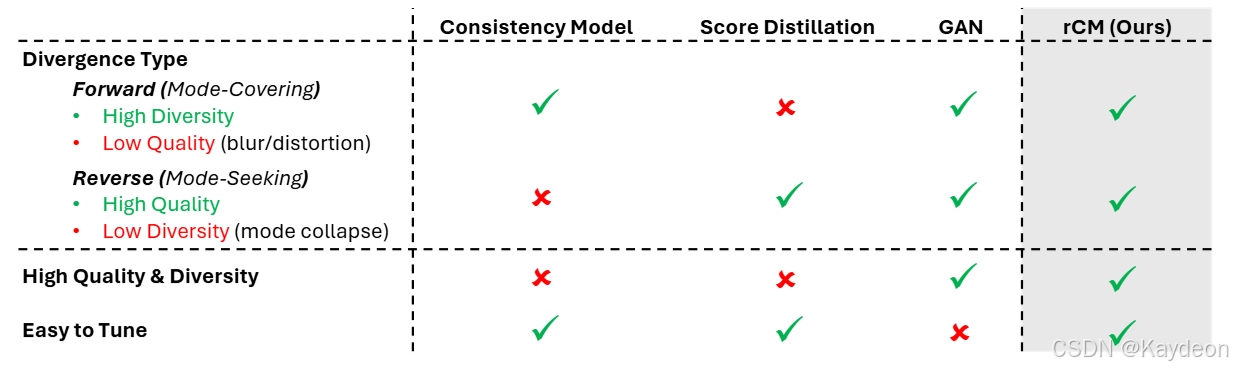
- 前向散度 vs 反向散度 : 作者从散度类型(Divergence Type)的角度对蒸馏方法进行了概念层面的划分。
- 前向散度 (Forward Divergence): 如 CMs,训练样本是真实数据或教师模型生成的数据。这种方法倾向于"模式覆盖",鼓励模型覆盖所有训练样本,但这常常导致密度分散和低质量样本。
- 反向散度 (Reverse Divergence): 如分数蒸馏,学生模型仅在自生成样本上进行监督。这种方法是"模式寻求"的,有利于提升视觉质量,但可能牺牲多样性(模式坍塌)。
- rCM 的提出: 为了修正 sCM 的质量问题,作者提出将分数蒸馏作为一个长跳跃正则化器,从而将 sCM 的前向生成路径与分数蒸馏的反向生成路径自然地结合起来。这个新框架被称为 rCM。
- rCM 无需多阶段训练、GAN 调优或复杂的超参数搜索,实验证明其在大规模模型上超越了 DMD2,在质量和多样性上均表现出色。
- 前向散度 vs 反向散度 : 作者从散度类型(Divergence Type)的角度对蒸馏方法进行了概念层面的划分。
第2章: 背景知识 (Background)
本章回顾了三个核心技术:扩散模型、一致性模型和分数蒸馏。
2.1 扩散模型 (Diffusion Models)
- 核心思想 : 通过逐步向干净数据 x 0 x_0 x0 添加高斯噪声来学习数据分布,然后学习逆转这个过程。
- 前向过程 : x t = α t x 0 + σ t ϵ x_t = \alpha_t x_0 + \sigma_t \epsilon xt=αtx0+σtϵ,其中 ϵ ∼ N ( 0 , I ) \epsilon \sim \mathcal{N}(0, I) ϵ∼N(0,I), α t \alpha_t αt 和 σ t \sigma_t σt 是预定义的噪声调度。
- 采样过程 (PF-ODE) : 采样过程可以遵循概率流常微分方程 (Probability Flow Ordinary Differential Equation, PF-ODE):
d x t = [ f ( t ) x t − 1 2 g 2 ( t ) ∇ x t log q t ( x t ) ] d t dx_t = \left[f(t)x_t - \frac{1}{2}g^2(t)\nabla_{x_t}\log q_t(x_t)\right]dt dxt=[f(t)xt−21g2(t)∇xtlogqt(xt)]dt
其中:- f ( t ) = d log α t d t f(t) = \frac{d\log\alpha_t}{dt} f(t)=dtdlogαt 和 g 2 ( t ) = d σ t 2 d t − 2 d log α t d t σ t 2 g^2(t) = \frac{d\sigma_t^2}{dt} - 2\frac{d\log\alpha_t}{dt}\sigma_t^2 g2(t)=dtdσt2−2dtdlogαtσt2 是与噪声调度相关的函数。
- ∇ x t log q t ( x t ) \nabla_{x_t}\log q_t(x_t) ∇xtlogqt(xt) 是分数函数 (score function)。
- 速度参数化 (Velocity Parameterization) : 模型可以被参数化为预测速度 v v v。此时,训练目标是最小化均方误差 (MSE):
E x 0 ∼ p d a t a , ϵ , t [ w ( t ) ∥ v θ ( x t , t ) − v ∥ 2 2 ] \mathbb{E}{x_0 \sim p{data}, \epsilon, t} \left[ w(t) \| v_\theta(x_t, t) - v \|_2^2 \right] Ex0∼pdata,ϵ,t[w(t)∥vθ(xt,t)−v∥22]
其中:- v θ ( x t , t ) v_\theta(x_t, t) vθ(xt,t) 是神经网络预测的速度。
- v = α ˙ t x 0 + σ ˙ t ϵ v = \dot{\alpha}_t x_0 + \dot{\sigma}_t \epsilon v=α˙tx0+σ˙tϵ 是回归的目标速度, f ˙ t \dot{f}_t f˙t 表示 f t f_t ft 对 t t t 的导数。
- 此时 PF-ODE 简化为 d x t d t = v θ ( x t , t ) \frac{dx_t}{dt} = v_\theta(x_t, t) dtdxt=vθ(xt,t),这被称为流匹配 (Flow Matching)。
2.2 一致性模型 (Consistency Models)
- 核心思想 : 学习一个一致性函数 f θ : ( x t , t ) ↦ x 0 f_\theta: (x_t, t) \mapsto x_0 fθ:(xt,t)↦x0,该函数能将教师模型 PF-ODE 轨迹上的任意点 ( x t , t ) (x_t, t) (xt,t) 直接映射回起点 x 0 x_0 x0。
- 离散时间 CM : 目标是让相邻时间步 t t t 和 t − Δ t t-\Delta t t−Δt 的输出保持一致。其损失函数为:
E x 0 ∼ p d a t a , ϵ , t [ w ( t ) d ( f θ ( x t , t ) , f θ − x ^ t − Δ t , t − Δ t ) ) ] ( 1 ) \mathbb{E}{x_0 \sim p{data}, \epsilon, t} \left[ w(t) d(f_\theta(x_t, t), f_{\theta-}\hat{x}_{t-\Delta t}, t-\Delta t)) \right] \quad (1) Ex0∼pdata,ϵ,t[w(t)d(fθ(xt,t),fθ−x^t−Δt,t−Δt))](1)
其中:- d ( ⋅ , ⋅ ) d(\cdot, \cdot) d(⋅,⋅) 是距离度量。
- θ − \theta^- θ− 是参数的停止梯度 (stop-gradient) 版本。
- x ^ t − Δ t \hat{x}_{t-\Delta t} x^t−Δt 是从 ( x t , t ) (x_t, t) (xt,t) 通过教师 PF-ODE 数值求解到 t − Δ t t-\Delta t t−Δt 得到的点。
- 连续时间 CM (sCM) : 当 D e l t a t → 0 Delta t \to 0 Deltat→0 时,离散时间 CM 升级为 sCM。损失函数简化为:
E [ w ( t ) f θ ( x t , t ) ⊤ d f θ − ( x t , t ) d t ] \mathbb{E} \left[ w(t) f_\theta(x_t, t)^\top \frac{df_{\theta-}(x_t, t)}{dt} \right] E[w(t)fθ(xt,t)⊤dtdfθ−(xt,t)]
其中 d f θ − ( x t , t ) d t \frac{df_{\theta-}(x_t, t)}{dt} dtdfθ−(xt,t) 是 f θ f_\theta fθ 沿着教师 ODE 轨迹的切线,可以通过链式法则计算,包含 JVP。通过特定的预处理,损失函数可以进一步简化为一个简单的 MSE 形式,强制执行瞬时自洽性。
2.3 分数蒸馏 (Score Distillation)
- 核心思想 : 旨在使学生模型分布 p θ p_\theta pθ 与教师模型分布 p t e a c h e r p_{teacher} pteacher 相匹配。
- 反向散度最小化 : 通过最小化某种反向散度来实现分布匹配:
min θ E t [ D f ( p θ t ∥ p t e a c h e r t ) ] ( 2 ) \min_\theta \mathbb{E}t [D_f(p\theta^t \| p_{teacher}^t)] \quad (2) θminEt[Df(pθt∥pteachert)](2)
其中:- D f D_f Df 是 f-散度。
- p θ t p_\theta^t pθt 和 p t e a c h e r t p_{teacher}^t pteachert 是在时间 t t t 对各自样本加噪后的分布。
- 实际操作 : 由于学生模型的分数 ∇ x t log p θ t ( x t ) \nabla_{x_t}\log p_\theta^t(x_t) ∇xtlogpθt(xt) 难以处理,通常会引入一个辅助的 "伪" 分数网络 (fake score network),它与学生模型通过对抗性方式联合优化。
第3章: 扩展 sCM (Scaling Up sCM)
本章详细介绍了作者如何将 sCM 扩展到大规模 T2I 和 T2V 任务,并在此过程中发现的问题。
3.1 算法细节 (Algorithm Details)
- 简化 sCM : 作者简化了原始 sCM 的实现,使其更具普适性。
- 适应任意噪声调度: 通过信噪比匹配,可以构建一个与 TrigFlow 兼容的 "包装" 教师模型,而无需重新训练原始教师模型。
- 简化损失函数 : 采用了切线归一化 (tangent normalization) 的 sCM 损失:
L s C M ( t h e t a ) = E x 0 ∼ p d a t a , ϵ , t ∼ p G [ ∥ F θ ( x t , t ) − F θ − ( x t , t ) − g ∥ g ∥ 2 2 + c ∥ 2 2 ] ( 4 ) \mathcal{L}{sCM}(theta) = \mathbb{E}{x_0 \sim p_{data}, \epsilon, t \sim p_G} \left[ \left\| F_\theta(x_t, t) - F_{\theta-}(x_t, t) - \frac{g}{\|g\|_2^2 + c} \right\|_2^2 \right] \quad (4) LsCM(theta)=Ex0∼pdata,ϵ,t∼pG[ Fθ(xt,t)−Fθ−(xt,t)−∥g∥22+cg 22](4)
其中:- F θ F_\theta Fθ 是速度预测器。
- g = w ( t ) d f θ − ( x t , t ) d t g = w(t) \frac{df_{\theta-}(x_t, t)}{dt} g=w(t)dtdfθ−(xt,t) 是加权后的切线。
- 分母 ∣ g ∥ 2 2 + c |g\|_2^2 + c ∣g∥22+c 起到了归一化的作用,使得损失值近似为 1,从而不再需要自适应加权。
3.2 基础设施 (Infrastructure)
为了支持大规模训练中的 JVP 计算,作者构建了专门的基础设施:
- FlashAttention-2 JVP 内核: 开发了一个 Triton 内核,将 JVP 计算集成到 FlashAttention-2 的前向传播中,支持自注意力和交叉注意力。
- 兼容 FSDP: 通过重构网络,将 JVP 计算限制在每个层内部,使其与完全分片数据并行 (Fully Sharded Data Parallel, FSDP) 兼容。
- 兼容 CP: 将该方案扩展到上下文并行 (Context Parallelism, CP),通过同样的方式分发 QKV 的切线,并使用新的 FlashAttention-2 JVP 内核进行局部注意力计算。
3.3 放大 sCM 的陷阱 (Pitfalls of Scaled-Up sCM)
- 实证观察:质量问题 :
- 尽管 sCM 生成的图像比离散 CM 更清晰,但在需要高精度或时间一致性的场景中,失真问题很严重。
- T2I: 在复杂提示(如渲染小文本)下,质量明显下降,且问题无法通过简单地增加模型大小来解决。
- T2V: 纹理模糊、物体几何形状不稳定(如物体穿透),导致明显的视觉失真。
- 理论分析:误差累积 :
- 作者将失真问题归因于误差累积。直观上,CM 试图一步求解教师 ODE,这相当于学习一个积分,误差会随着积分区间(即时间 t t t)的增大而累积。
- sCM 的学习目标包含一个由 JVP 引入的一阶自反馈信号 f r a c d F θ − d t frac{dF_{\theta-}}{dt} fracdFθ−dt。这个信号在 BF16 这样的低精度计算下数值上很脆弱。
- 随着训练进行,误差会从小 t t t 传播到大 t t t,并被自反馈放大。当 t t t 很大时,来自教师模型的监督信号会减弱,学习动态主要由 JVP 主导,导致误差累积。
第4章: 分数正则化的连续时间一致性模型 (Score-Regularized Continuous-Time Consistency Models)
本章介绍了核心方法 rCM,旨在修复 sCM 的质量问题。
4.1 用分数正则化修复质量 (Quality Repair with Score Regularization)
-
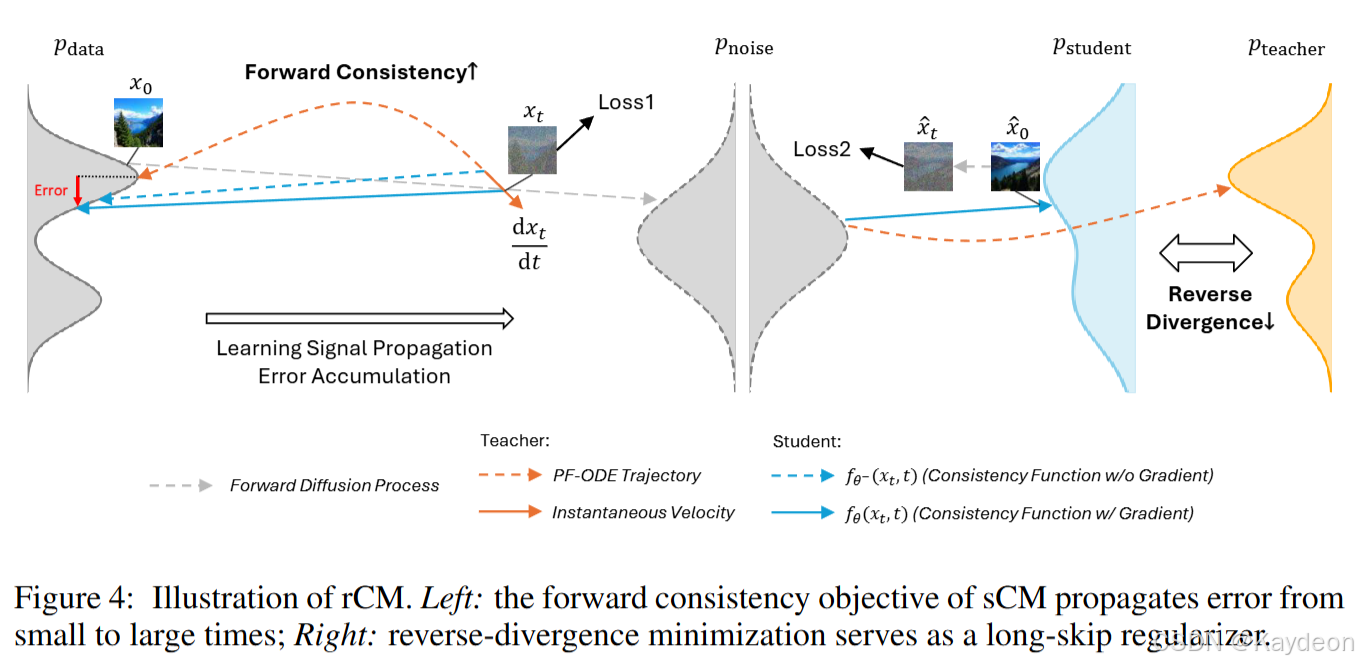
核心思想: 如图4所示,通过引入基于分数的长跳跃正则化来缓解 sCM 的质量限制,这为 sCM 补充了反向散度。
-
rCM 目标函数 : 最终的 rCM 损失是 sCM 损失和 DMD 损失的加权和:
L r C M ( θ ) = L s C M ( θ ) + λ L D M D ( θ ) \mathcal{L}{rCM}(\theta) = \mathcal{L}{sCM}(\theta) + \lambda \mathcal{L}_{DMD}(\theta) LrCM(θ)=LsCM(θ)+λLDMD(θ)其中 l a m b d a lambda lambda 是平衡权重,经验上设为 0.01 即可在所有模型和任务上通用。
-
Rollout 策略:
- DMD 损失需要学生模型生成的样本 x 0 ∼ p θ x_0 \sim p_\theta x0∼pθ。
- 作者采用随机步数 ( N (N (N 从 [ 1 , N m a x ] [1, N_{max}] [1,Nmax] 中随机选择) 和随机时间步的采样策略,以确保学生模型能探索整个时间范围。
4.2 稳定的时间导数计算 (Stable Time Derivative Calculation)
为了稳定 JVP 计算,防止长时间训练后模型崩溃,作者提出了两种即插即用的技术:
- 半连续时间 (Semi-Continuous Time) : 对 JVP 中的空间导数项 ∇ x t ( F θ − ) F t e a c h e r \nabla_{x_t}(F_{\theta-})F_{teacher} ∇xt(Fθ−)Fteacher 精确计算,而对时间偏导数项 ∂ t F θ − \partial_t F_{\theta-} ∂tFθ− 使用有限差分进行近似。
- 高精度时间 (High-Precision Time): 对于 100 亿以上参数的模型和视频任务,强制所有时间嵌入层使用 FP32 精度进行计算,以确保 rCM 训练的稳定性。
第5章: 实验 (Experiments)
本章通过在大型 T2I 和 T2V 模型上的实验来验证 rCM 的可扩展性和性能。
5.1 实验设置 (Experimental Setups)
- 模型与任务: 在 Cosmos-Predict2 (0.6B, 2B, 14B) T2I 模型和 Wan2.1 (1.3B, 14B) T2V 模型上进行蒸馏。
- 实现: 基于 Cosmos-Predict2 代码库,并支持 FSDP2、Ulysses CP 等基础设施。采用全参数微调,而非 LoRA。
- 评估指标 :
- T2I: 使用 GenEval 评估模型在复杂组合提示下的表现(如物体计数、空间关系等)。
- T2V: 使用 VBench 系统地评估运动质量和语义对齐。
5.2 结果 (Results)
- 性能 :
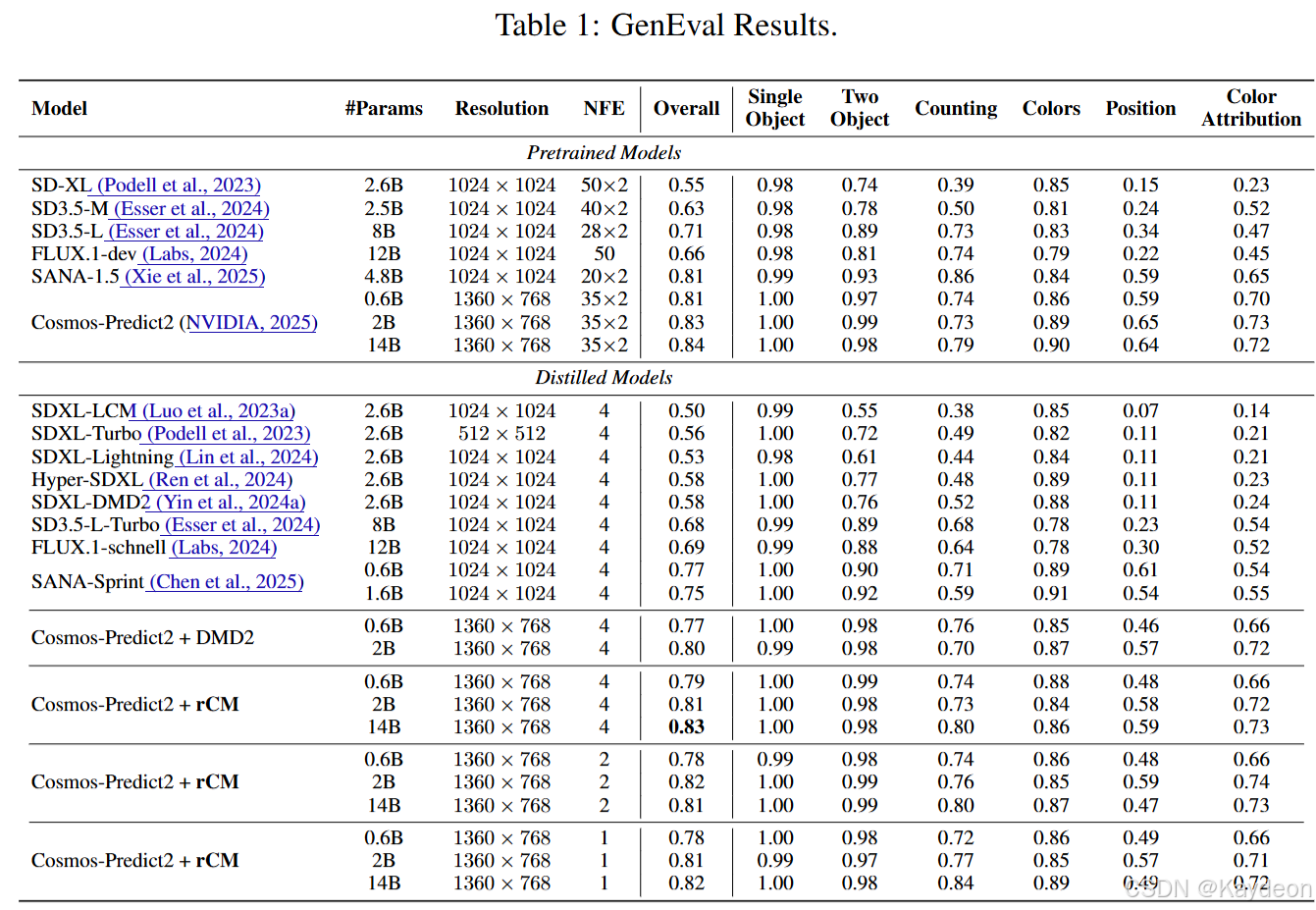
- T2I (表1): rCM 在 Cosmos-Predict2 上的性能接近教师模型,并且随着模型规模扩大而提升。14B 模型仅用 4 步就达到了 0.83 的 GenEval SOTA 分数。在渲染小文本等挑战性任务上,视觉质量与 FLUX.1-schnell 相当。
- T2V (表2, 表3): rCM 在 480p 的 Wan 模型上甚至在 VBench 指标上超越了教师模型。在 720p 的 Cosmos-Predict2 T2V 和 I2V 任务上也观察到类似现象。
- 与 DMD2 的比较 :
- 质量: 在 GenEval 和 VBench 指标上,rCM 与 DMD2 相当甚至更优。
- 多样性 (图1): rCM 显示出明显的多样性优势。它保留了 sCM 的多样性,同时解决了其视觉质量问题。相比之下,DMD2 倾向于产生模式坍塌的生成结果,多样性较低。
- 更少步数生成 (图6) :
- T2I: rCM 在 1-4 步都能生成合理的样本,即使在 1 步或 2 步设置下,GenEval 分数也仅轻微下降。
- T2V: 任务更具挑战性。1 步生成结果模糊,VBench 分数显著下降。2 步生成已经接近教师模型水平,而 4 步则能进一步完善细节。
第6章: 结论 (Conclusion)
论文提出了 rCM,一个将扩散蒸馏扩展到大型图像和视频模型的框架。通过结合基于前向散度的一致性蒸馏和基于反向散度的分数蒸馏,rCM 解决了 sCM 的质量问题,并展现出比 DMD2 更优的多样性。蒸馏后的模型在单步 T2I 和两步 T2V 任务上取得了有竞争力的结果,实现了高达 50 倍的加速。