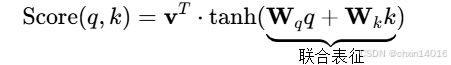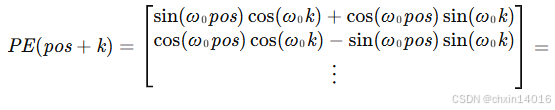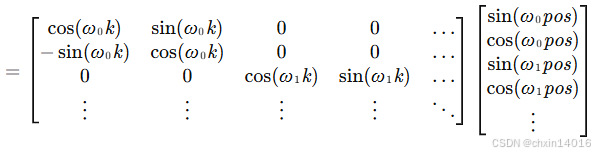环境:PyCharm + python3.8
👉【注意力机制】
- 注意力机制:本质是软性最近邻回归,权重由参数化的核函数生成。
查询(Queries)、键(Keys) 和 值(Values) 的形状解析
在注意力机制中,查询(Queries)、键(Keys) 和 值(Values) 的形状可以不同,但需满足一定的逻辑关系。
输入形状说明
queries(查询) :(2, 1, 20)
含义:2个样本(batch_size=2),每个样本有1个查询(num_queries=1),每个查询的特征维度是20(query_size=20)。
适用场景:比如在机器翻译中,解码器(Decoder)的当前隐藏状态作为查询(1个查询),去关注编码器(Encoder)的所有隐藏状态(多个键值对)。
keys(键) :(2, 10, 2)
含义:2个样本,每个样本有10个键(num_kv_pairs=10),每个键的特征维度是2(key_size=2)。
适用场景:比如编码器的10个时间步的隐藏状态(每个隐藏状态是2维向量)。
values(值) :(2, 10, 4)
含义:2个样本,每个样本有10个值(num_kv_pairs=10),每个值的特征维度是4(value_size=4)。
适用场景:比如编码器的10个时间步的隐藏状态(每个隐藏状态是4维向量)。
为什么键和值的特征维度可以不同?
键(Key)的作用是计算与查询(Query)的相似度(注意力分数),因此它只需要包含足够的信息来计算相关性,维度可以较小(如2维)。
值(Value)的作用是存储最终要传递给输出的信息,因此它可能需要更高的维度(如4维)来编码更丰富的信息。
类比:
键(Key) 就像一本书的目录(简短描述,用于快速查找)
值(Value) 就像书的正文内容(详细描述,用于最终阅读)
注意力机制设计理念的演进
第一代:基于"差异" 的注意力(相似度计算)
- 直接相减,
- 再软分类成为注意力权重后,
- 对值进行加权求和得到预测值。
- 直接相减,计算距离
- 局限性:
- 只能捕捉简单的线性关系
- 对于复杂的语义匹配不够灵活
第二代:基于"联合表征" 的加性注意力
- 查询和键 映射到同一空间(转成相同维度)后,
- 再相加结合(广播求和)成为特征,
- 再掩码软分类成为注意力权重,
- 再对值进行加权求和得到预测值。
两个不同维度的查询与键映射到同一维度后相加(创建新表征)
联合表征(两个不相似的向量组合在一起可能产生有意义的表征)
非线性交互 :
tanh激活函数可以捕捉复杂的交互模式参数化灵活性 :
W_q,W_k可以学习为不同特征分配不同重要性类比:
做菜时,不是比较西红柿和鸡蛋有多像
而是看它们组合在一起(西红柿炒鸡蛋)好不好吃
第三代:基于"矩阵乘法" 的点积注意力
- 对每个查询向量和键向量计算点集分数(即查询和键的相似度)
- 计算点积时用缩放因子稳定训练过程,
- 再对前面得到的点积分数 掩码软分类成为注意力权重,
- 再对值进行加权求和得到预测值。
点积:逐元素相乘再求和(核心思想:"用最数学本质的方式计算相关性")
数学本质:点积本身就是衡量两个向量方向相似性的最直接方式
计算效率:矩阵乘法是硬件加速最好的操作
可解释性:点积结果直接反映向量在每个维度上的对齐程度
理论证明:当查询和键是独立随机变量时,点积是最优的相似度度量
采用缩放因子后的缩放点积注意力:
解决高维空间中点积方差过大的问题
让注意力分布更加"平和",避免极端值
点积注意力并没有完全放弃"联合表征"的思想,而是通过多头机制来实现:
每个头学习一种不同的"联合表征"方式
通过多个注意力头来捕捉不同类型的交互模式
经典注意力框架回顾
- 注意力提示(Attention Cues) :
- 自上而下(Top-down):目标驱动的注意力(如主动搜索特定物体)。
- 自下而上(Bottom-up):显著性驱动的注意力(如被突发运动吸引)。
1. 注意力提示
注意力经济的背景
- 稀缺性:注意力是有限的、有价值的资源,需通过机会成本(如时间、选择)支付。
- 商业模式驱动:现代经济中,注意力被商品化(如广告、付费隐藏广告、游戏内购),用户需通过消耗注意力或金钱交换服务。
- 信息过载挑战 :人类感官系统接收的信息远超处理能力,需高效分配注意力以生存和发展。
- 如 人类的视觉神经系统大约每秒收到
位的信息,远超过大脑能完全处理的水平。
1.1. 生物学中的注意力提示
注意力是如何应用于视觉世界中的呢?
双组件(two-component)框架:
- 起源:由"美国心理学之父" 威廉·詹姆斯(19世纪90年代)提出,解释人类如何选择性聚焦视觉信息。
- 在这个框架中,受试者基于非自主性提示 和 自主性提示 有选择地引导注意力的焦点。
- 非自主性提示(Bottom-up Cues) :基于环境中物体的突出性和易见性**【一眼看到】**
- 定义:由环境中物体的显著性(如颜色、大小、运动)自发吸引注意力。
- 示例:红色咖啡杯 在 黑白背景中自动吸引目光(图10.1.1)。
- 特点:快速、无意识、基于感官刺激。
- 自主性提示(Top-down Cues) :【主动去找】
- 定义:由任务、目标或主观意愿驱动,主动引导注意力。
- 示例:喝咖啡后想读书,主动将视线转向书本(图10.1.2)。
- 特点:缓慢、有意识、依赖认知控制。
非自主性提示:基于环境中物体的突出性和易见性。
- 假设面前有五个物品:一份报纸、一篇研究论文、一杯咖啡、一本笔记本和一本书,如 图10.1.1。
- 纸制品皆为黑白印刷,但咖啡杯为红色。
- 即 咖啡杯在这种视觉环境中是突出和显眼的,不由自主地引起人们的注意。
- 所以我们会把视力最敏锐的地方放到咖啡上, 如 图10.1.1所示。
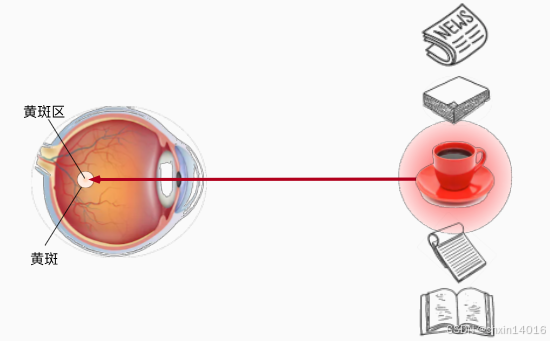 图10.1.1
图10.1.1
由于 突出性的非自主性提示(红杯子),注意力不自主地指向了咖啡杯
- 喝咖啡后想读书,所以转过头,重新聚焦眼睛,然后看看书,如 图10.1.2。
- 与 图10.1.1中由于突出性导致的选择不同,此时选择书是受到了认知和意识的控制,
- 因此注意力在基于自主性提示去辅助选择时将更为谨慎。
- 受试者的主观意愿推动,选择的力量也就更强大。
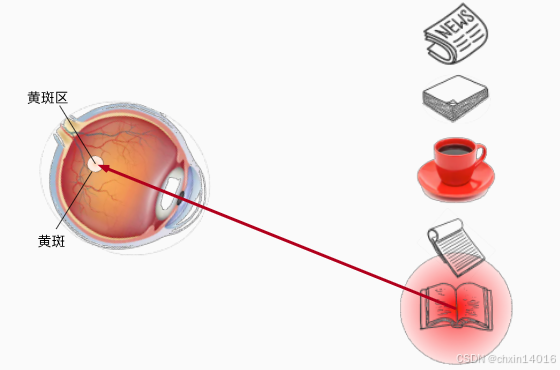 图10.1.2
图10.1.2
依赖于 任务的意志提示(想读一本书),注意力被自主引导到书上
1.2. 查询、键和值
- 自主性的 与 非自主性 的注意力提示 解释了人类的注意力的方式,可以通过这两种注意力提示,用神经网络来设计注意力机制的框架 ↓
- 若只使用非自主性提示 (将选择偏向于感官输入),
- 则可简单地使用参 数化的全连接层,
- 甚至是 非参数化的最大汇聚层或平均汇聚层。
因此,"是否包含自主性提示"将注意力机制与全连接层或汇聚层区别开来。
- 从生物学到计算的映射 :
- 非自主性提示 → 键(Key):感官输入的显著性特征 (如颜色、位置)作为键,用于被动匹配。
- 自主性提示 → 查询(Query):任务或目标驱动的提示,主动搜索相关信息。
- 感官输入 → 值(Value) :待选择的特征或数据,根据查询 与键的匹配程度 被加权聚合。
- 更通俗的解释,每个值都与一个键配对,这可以想象为感官输入的非自主提示。
- 注意力汇聚(Attention Pooling) :
- 将选择引导至感官输入(sensory inputs,例如中间特征表示),即 将选择引导至值。
- 机制:通过计算查询与键的相似性(如点积、多层感知机),生成权重,对值加权求和。
如 图10.1.3所示,可以通过设计注意力汇聚的方式,便于给定的查询(自主性提示)与键(非自主性提示)进行匹配, 这将引导得出最匹配的值(感官输入)。
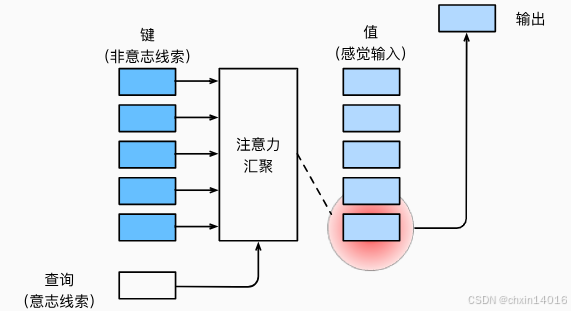 图10.1.3 注意力机制通过 注意力汇聚
图10.1.3 注意力机制通过 注意力汇聚
将 查询 (自主性提示)和 键 (非自主性提示)结合在一起,
实现对 值(感官输入)的选择倾向
鉴于上面所提框架在 图10.1.3中的主导地位,因此这个框架下的模型将成为本章的中心。然而,注意力机制的设计有许多替代方案。例如可以设计一个不可微的注意力模型,该模型可以使用强化学习方法 (Mnih et al., 2014)进行训练。
1.3. 注意力的可视化
- 平均汇聚层可以被视为 输入的加权平均值,其中各输入的权重是一样的。
- 实际上,注意力汇聚得到的是 加权平均的总和值,
- 其中权重是在给定的查询和不同的键之间计算得出的。
python
import torch
import common定义show_heatmaps函数:
- 作用:可视化注意力权重。
- 输入:
matrices:形状为(要显示的行数,要显示的列数,查询的数目,键的数目)
python
def show_heatmaps(matrices, xlabel, ylabel, titles=None, figsize=(2.5, 2.5),
cmap='Reds'):
""" 显示矩阵热图
matrices: 4D数组 (要显示的行数,要显示的列数,查询的数目,键的数目)
可以是PyTorch张量或NumPy数组
xlabel (str) : x轴标签
ylabel (str) : y轴标签
titles (list) : 子图标题列表(可选,数量应等于要显示的列数)
figsize (tuple) : 每个子图的图形大小(英寸)
cmap (str) : 颜色映射名称(如'Reds', 'viridis')
SVG(Scalable Vector Graphics,可缩放矢量图形)适合简单图形(图标、图表、Logo),基于XML的矢量图形格式
"""
# 设置Matplotlib使用SVG后端(在Jupyter或PyCharm中生效)
plt.rcParams['figure.dpi'] = 100 # 可选:调整分辨率
plt.rcParams['svg.fonttype'] = 'none' # 确保文本可编辑(SVG 特性)
plt.rcParams['figure.facecolor'] = 'white' # 可选:设置背景色
# 获取矩阵的行数和列数
num_rows, num_cols = matrices.shape[0], matrices.shape[1]
# 创建子图
fig, axes = plt.subplots(num_rows, num_cols, # 子图的行数和列数
figsize=figsize, # 图形大小(宽, 高)
sharex=True, sharey=True, # 所有子图 共享xy轴(避免重复标签)
squeeze=False) # squeeze=False 强制axes始终是二维,即使只有一行或一列
pcm = None # 初始化一个pcm变量用于颜色条
# 遍历所有子图
for i in range(num_rows):
for j in range(num_cols):
ax = axes[i, j] # 获取当前子图
matrix = matrices[i, j] # 获取当前子图对应的矩阵 (查询数×键数)
# 处理不同类型的输入
if hasattr(matrix, 'detach'): # 如果是PyTorch张量
matrix_data = matrix.detach().numpy()
elif isinstance(matrix, np.ndarray): # 如果是NumPy数组
matrix_data = matrix
else: # 其他类型尝试转换为NumPy数组
matrix_data = np.array(matrix)
pcm = ax.imshow(matrix_data, cmap=cmap) # 绘制热图,cmap为颜色映射
# 设置标签(只在边缘子图显示)
if i == num_rows - 1:
ax.set_xlabel(xlabel) # Keys
if j == 0:
ax.set_ylabel(ylabel) # Queries
# 设置标题(使用titles[j]确保每列标题一致)
if titles and j < len(titles):
ax.set_title(titles[j])
plt.tight_layout() # 调整布局防止重叠
# 添加全局颜色条(使用最后一个子图的pcm)
if pcm is not None:
# shrink=0.6 颜色条的长度比例缩放,缩小为60%
# location='right' 颜色条位置处右侧
fig.colorbar(pcm, ax=axes, shrink=0.6, location='right')
plt.show()下面使用一个简单的例子进行演示:
- 在本例子中,仅当查询和键相同时,注意力权重为1,否则为0。
python
# print(f"10x10 的单位矩阵(对角线为 1,其余为 0):\n{torch.eye(10)}")
# 仅当查询和键相同时,注意力权重为1,否则为0
# torch.eye(10): 生成一个 10x10 的单位矩阵(对角线为 1,其余为 0)
# .reshape((1,1,10,10)): 调整形状为(batch_size=1,num_heads=1,seq_len=10,seq_len=10)
# 模拟一个单头注意力机制的权重矩阵(Queries × Keys)
attention_weights = torch.eye(10).reshape((1, 1, 10, 10))
common.show_heatmaps(attention_weights, xlabel='Keys', ylabel='Queries')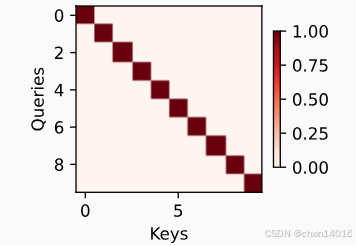
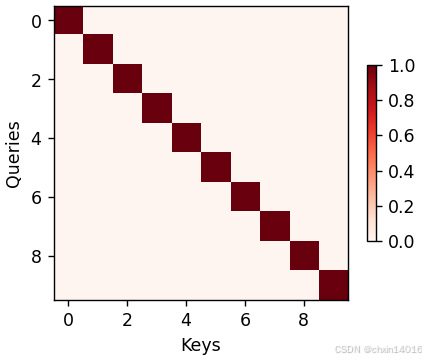
后面将频繁调用show_heatmaps函数来显示注意力权重。
小结
人类的注意力是有限的、有价值和稀缺的资源。
受试者使用非自主性和自主性提示有选择性地引导注意力。前者基于突出性,后者则依赖于意识。
注意力机制与全连接层或者汇聚层的区别源于增加的自主提示。
由于包含了自主性提示,注意力机制与全连接的层或汇聚层不同。
注意力机制通过注意力汇聚使选择偏向于值(感官输入),其中包含查询(自主性提示)和键(非自主性提示)。键和值是成对的。
可视化查询和键之间的注意力权重是可行的。
2. 注意力汇聚:Nadaraya-Watson 核回归
核回归:
- 是一种非参数回归方法
- 它无需对数据之间的关系形式做出任何假设,而是通过核函数来估计数据的条件期望。
- 作用:将输入变量映射到一个高维特征空间中,在这个空间中进行线性回归。
- 目标:通过加权平均的方式来估计条件期望。
- 适用于估计变量之间的依赖关系,特别是当数据点稀疏或模型形式未知时。
上节介绍了框架下的注意力机制的主要成分 图10.1.3:
- 查询(自主提示)和 键(非自主提示)之间的交互形成了注意力汇聚;
- 注意力汇聚有选择地聚合了值(感官输入)以生成最终的输出。
1964年提出的Nadaraya-Watson核回归模型 是一个简单但完整的例子,可用于演示具有注意力机制的机器学习。
python
import torch
from torch import nn
import matplotlib.pyplot as plt
import common2.1. 生成数据集
考虑下面这个回归问题:
- 给定的成对的"输入-输出"数据集
,
- 学习
来预测任意新输入
的输出
:
根据下面的非线性函数生成一个人工数据集,其中加入的噪声项为 ε:
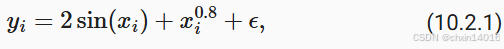
- 噪声项 ε 服从均值为0 和 标准差为0.5 的正态分布
这里生成 50个训练样本 和 50个测试样本。并将训练样本排序,以更好地可视化之后的注意力模式:
python
n_train = 50 # 训练样本数
x_train, _ = torch.sort(torch.rand(n_train) * 5) # 排序后的训练样本(以便可视化)
def f(x): # 非线性函数
return 2 * torch.sin(x) + x**0.8
y_train = f(x_train) + torch.normal(0.0, 0.5, (n_train,)) # 训练样本的输出(添加噪声项)
x_test = torch.arange(0, 5, 0.1) # 测试样本
y_truth = f(x_test) # 测试样本的真实输出
n_test = len(x_test) # 测试样本数
print(f"测试样本数:{n_test}")
下面的函数:
- 功能:绘制所有的训练样本(样本由圆圈表示)
- 使用不带噪声项的真实数据生成函数
(标记为"Truth")
- 学习得到的预测函数(标记为"Pred")
python
def plot_kernel_reg(x_test, y_truth, y_hat,
x_train, y_train):
'''绘制所有的训练样本(样本由圆圈表示)
不带噪声项的真实数据生成函数 f(标记为"Truth")
学习得到的预测函数(标记为"Pred")
y_hat :预测值数组
x_train :训练数据x坐标
y_train :训练数据y坐标
x_test :测试数据x坐标(用于绘制真实曲线和预测曲线)
y_truth :真实值数组(对应x_test)
'''
# 使用 constrained_layout 替代 tight_layout
plt.figure(figsize=(4, 3), constrained_layout=True) # 启用约束布局
# 绘制 测试数据的真实输出 和 预测输出
plt.plot(x_test, y_truth, label='Truth', linestyle='-', linewidth=1)
plt.plot(x_test, y_hat, label='Pred', linestyle='--', linewidth=1, color='m')
# plot(x_test, [y_truth, y_hat], 'x', 'y', legend=['Truth', 'Pred'], xlim=[0, 5], ylim=[-1, 5])
# 绘制 训练数据信息
# plt.plot(x_train, y_train, 'o', alpha=0.5, label='Train Data')
plt.scatter(x_train, y_train, color='orange', alpha=0.5, label='Train Data')
# 设置图形属性
plt.xlabel('x')
plt.ylabel('y')
plt.xlim(0, 5)
plt.ylim(-1, 5)
plt.legend()
plt.grid(True)
plt.title('Kernel Regression Comparison')
# plt.tight_layout() # 调整布局防止标签被截断
plt.show()
python
def plot_kernel_reg(y_hat):
common.plot_kernel_reg(x_test, y_truth, y_hat, x_train, y_train)2.2. 平均汇聚
先使用最简单的估计器来解决回归问题。基于平均汇聚来计算所有训练样本输出值的平均值:

如下图所示,这个估计器确实不够聪明。
- 真实函数
("Truth")和预测函数("Pred")(紫色线)相差很大。
python
# .repeat_interleave() 用于重复张量元素
# 计算出训练样本标签y的均值,然后将其重复n_test次,返回一个长度为n_test的 1D张量
# 即,生成一个长度为 n_test 的张量,所有元素为 y_train的均值,即 y_train.mean()
y_hat = torch.repeat_interleave(y_train.mean(), n_test)
# plot_kernel_reg(y_hat)
common.plot_kernel_reg(x_test, y_truth, y_hat, x_train, y_train)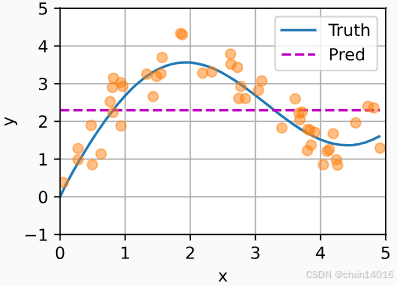
2.3. 非参数注意力汇聚
- 平均汇聚 忽略输入信息,即 忽略了输入
。
- Nadaraya (Nadaraya, 1964)和 Watson (Watson, 1964) 提出
- Nadaraya-Watson 核回归 (Nadaraya-Watson kernel regression):
- 根据输入位置 对输出
进行加权,
- 根据输入位置 对输出
- 即 公式 (10.2.3)所描述的估计器 👇
- Nadaraya-Watson 核回归 (Nadaraya-Watson kernel regression):
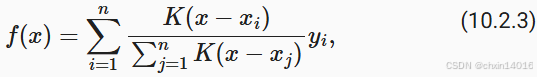
- 其中
是核(kernel)
基于该 核函数,可以从 图10.1.3中的注意力机制框架的角度 重写 (10.2.3),成为一个更通用的注意力汇聚(attention pooling)公式:
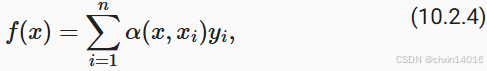
:查询
:键值对
比较 (10.2.4)和 (10.2.2),注意力汇聚 是 的加权平均,通过将 查询
和 键
间的关系建模为 注意力权重 (attention weight)
,且该权重对于任何查询 在所有键值对上 构成有效概率分布(非负且总和为 1)。
- 如 (10.2.4)所示,注意力权重 将被分配给 每一个对应值
。
- 对于任何查询,模型在所有键值对注意力权重都是一个有效的概率分布:非负且总和为1。
为了更好地理解注意力汇聚,下面考虑一个高斯核(Gaussian kernel),其定义为:
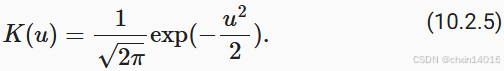
将高斯核代入 注意力汇聚公式 (10.2.4) 和 核回归 (10.2.3) 可以得到:
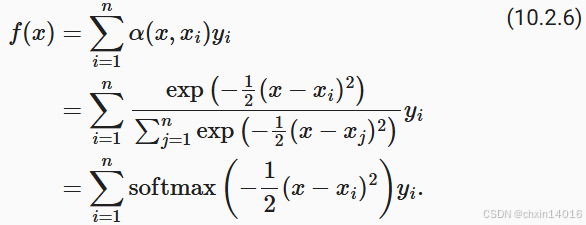
(基于高斯核注意力机制)
在 (10.2.6)中, 若一个键 越是接近给定的查询
,则分配给这个键对应值
的注意力权重就会越大, 也就"获得了更多的注意力"。
- 即 键
越接近查询
,对应值
获得的注意力权重越大。(相似度越高,权重越大)
- 核心思想 :
- 通过计算测试样本 (
x_test) 与 训练样本 (x_train) 之间的相似度(注意力权重), - 对训练标签 (
y_train) 进行加权平均得到预测值 (y_hat)
- 通过计算测试样本 (
Nadaraya-Watson核回归是一个非参数模型,所以 基于此的 (10.2.6)是 非参数的注意力汇聚(nonparametric attention pooling)模型。
- 下面基于这个非参数的注意力汇聚模型来绘制预测结果。
步骤:
- 重复x_test,以匹配注意力权重的形状
- 计算注意力权重(高斯核软注意力)
- 加权平均得到预测值
python
# 👉 非参数注意力汇聚
# 1. 重复x_test以匹配注意力权重的形状
# 为每个测试样本生成一个与 x_train 对齐的矩阵,便于后续计算相似度
# X_repeat的形状:(n_test,n_train),
# 每一行都包含着相同的测试输入(例如:同样的查询)
# x_test.repeat_interleave(n_train) 对张量x_test的每个元素沿指定维度(默认0)重复n_train次
# 即 每个测试样本重复 n_train 次(展平为一维)
# .reshape((-1, n_train)) 将展平的张量重新调整为(n_test, n_train),其中每一行是x_test的一个副本 重复n_train次
X_repeat = x_test.repeat_interleave(n_train).reshape((-1, n_train))
print(f"测试数据形状x_test.shape:{x_test.shape}")
print(f"将测试数据元素重复后形状 x_test.repeat_interleave(n_train).shape:"
f"{x_test.repeat_interleave(n_train).shape}")
print(f"重塑形状为(n_test,n_train)以便后续计算相似度(相似度越高,注意力权重越大)\n"
f"x_test.repeat_interleave(n_train).reshape((-1, n_train)).shape:"
f"{x_test.repeat_interleave(n_train).reshape((-1, n_train)).shape}")
# 2. 计算注意力权重(高斯核软注意力)
# x_train包含着键。attention_weights的形状:(n_test,n_train),
# 每一行都包含着要在给定的每个查询的值(y_train)之间分配的注意力权重
# -(X_repeat - x_train)**2 / 2 计算测试样本与训练样本之间的负欧氏距离(高斯核的指数部分)
# 测试数据的输入X_repeat 相当于 查询
# 训练数据的输入x_train 相当于 键
attention_weights = nn.functional.softmax(
-(X_repeat - x_train)**2 / 2, # 高斯核(负欧氏距离),相似度计算:距离越小,相似度越高(权重越大)
dim=1) # 对每一行(每个测试样本)做softmax归一化,确保权重和为1
# 3. 加权平均得到预测值
# y_hat的每个元素都是值的加权平均值,其中的权重是注意力权重
# 左:每个测试样本 对应所有训练标签的各个注意力权重
# 右:每个训练样本对应的标签
y_hat = torch.matmul(attention_weights, y_train) # 矩阵乘法:左找行,右找列
plot_kernel_reg(y_hat)
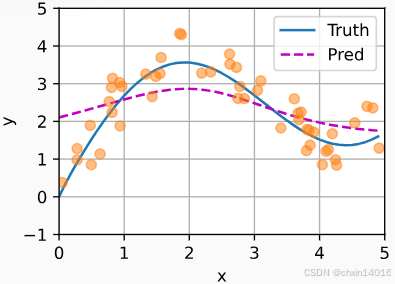
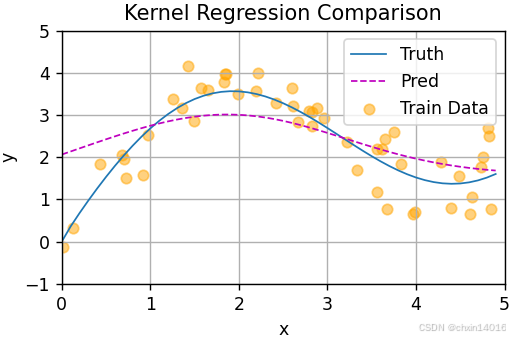
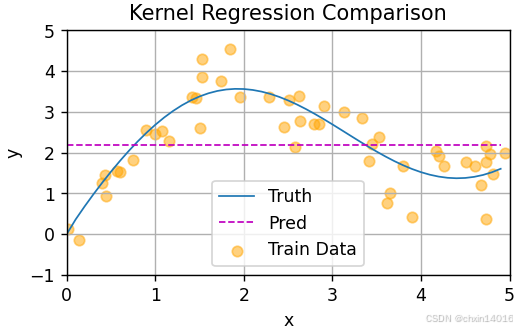
从绘制的结果会发现:
- 新的模型预测线(紫色线)是平滑的,
- 且比平均汇聚的预测更接近真实。
现在来观察注意力的权重:这里
- 测试数据的输入 相当于 查询
- 训练数据的输入 相当于 键
- 因为两个输入都是经过排序的,因此由观察可知"查询-键"对越接近,注意力汇聚的注意力权重就越高。
python
# np.expand_dims(attention_weights, 0) 在第0轴(最外层)扩展新维度
# np.expand_dims(np.expand_dims(attention_weights,0),0) 连续两次在第0轴(最外层)扩展新维度
# 假设attention_weights原始维度是(3,4),则第一次扩展变成(1,3,4),则第一次扩展变成(1,1,3,4)
common.show_heatmaps(np.expand_dims(np.expand_dims(attention_weights, 0), 0),
xlabel='Sorted training inputs',
ylabel='Sorted testing inputs') # 显示注意力权重的矩阵热图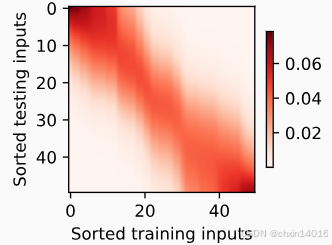
2.4. 带参数注意力汇聚
- 非参数的Nadaraya-Watson核回归 具有一致性 (consistency)的优点 :
- 若有足够的数据,此模型会收敛到最优结果。
- 尽管如此,我们还是可以轻松地将可学习的参数集成到注意力汇聚中。
例如,与 (10.2.6)略有不同,在下面的 查询 和 键
之间的距离乘以可学习参数
:
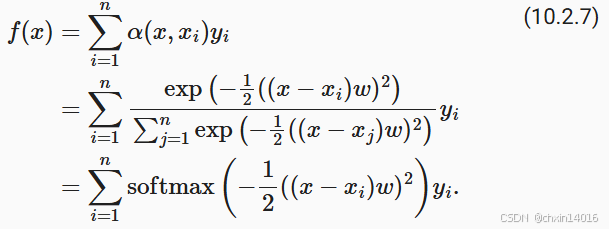
- 自注意力机制:通过掩码排除自身匹配,强制模型关注其他样本,防止过拟合(mask)
- 高斯核作用:距离越近的键值对获得更高权重(通过softmax归一化)
- 可学习参数w:控制高斯核的带宽,影响相似度计算敏感度
- 批量处理能力:通过矩阵运算支持同时处理多个查询点
本节的余下部分将通过训练这个模型 (10.2.7)来学习注意力汇聚的参数。
2.4.1. 批量矩阵乘法
可以利用深度学习开发框架中提供的批量矩阵乘法,来更有效地计算小批量数据的注意力。
假设:
- 第一个小批量数据 :包含n个矩阵
,形状为 a×b
- 第二个小批量 :包含n个矩阵
,形状为 b×c
- 它们的批量矩阵乘法 得到n个矩阵
,形状为 a×c。
- 因此,
- 假定两个张量的形状分别是
和
,
- 它们的批量矩阵乘法输出的形状为
。
- 假定两个张量的形状分别是
python
X = torch.ones((2, 1, 4))
Y = torch.ones((2, 4, 6))
print(f"批量矩阵乘法bmm后,结果矩阵形状:{torch.bmm(X, Y).shape}")
在注意力机制的背景中,可以使用小批量矩阵乘法来计算小批量数据中的加权平均值:
python
# 演示注意力机制中的加权求和
weights = torch.ones((2, 10)) * 0.1 # 形状: (批量大小, 序列长度)-注意力权重
values = torch.arange(20.0).reshape((2, 10)) # 形状: (批量大小, 序列长度)-值向量
# .unsqueeze()在指定位置增加维度
print(f"在指定位置增加维度后矩阵形状:\n"
f"weights:{weights.unsqueeze(1).shape}\n"
f"values :{values.unsqueeze(-1).shape}")
print(f"增加维度后 进行 批量矩阵乘法bmm,结果为:\n"
f"使用bmm计算加权和: 权重(2,1,10) × 值(2,10,1) = 结果(2,1,1) \n"
f"{torch.bmm(weights.unsqueeze(1), values.unsqueeze(-1))}")
2.4.2. 定义模型
基于 (10.2.7)中的 带参数的注意力汇聚,使用小批量矩阵乘法, 定义Nadaraya-Watson核回归的带参数版本为:
python
class NWKernelRegression(nn.Module):
''' Nadaraya-Watson 核回归模型,实现基于注意力机制的核回归
实现Nadaraya-Watson核回归的非参数方法,通过注意力机制对输入数据进行加权平均
使用高斯核函数来计算查询与键之间的相似度,并将这些相似度作为权重对值进行加权求和
'''
def __init__(self, **kwargs):
super().__init__(**kwargs)
# 可学习的参数 (高斯核的带宽参数),即 查询与键间距离要乘以的权重
self.w = nn.Parameter(torch.rand((1,), requires_grad=True))
def forward(self, queries, keys, values):
'''
queries : 查询输入 (n_query,),有n_query个查询
keys : 训练输入 (n_query, n_train),即 每个查询对应n_train个键
values : 训练输出 (n_query, n_train)
# queries 和 attention_weights的形状为 (查询个数,"键-值"对个数)
返回: 加权求和后的预测值 (n_query,)
'''
# 扩展 查询向量queries形状 以匹配 键值对keys的维度
# queries形状: (查询个数,) -> 扩展为 (查询个数, 键值对个数)
# 将查询的每个元素重复 键的列数次(为了当前查询与每个键做差)
# 然后将查询的形状重塑为 列维与键的行维相等的 矩阵形式 (第i行元素皆为第i个查询)
# 由此可使查询拥有 与键相同的形状,以便后续做差计算
queries = queries.repeat_interleave(keys.shape[1]).reshape((-1, keys.shape[1]))
# 计算注意力权重(使用高斯核函数)
# 公式: attention = softmax(-(query - key)^2 * w^2 / 2)
# 注意力权重通过高斯核 exp(-(x_query-x_key)^2 / (2σ^2)) 计算,
# 使用softmax进行归一化,确保所有权重之和为1
self.attention_weights = nn.functional.softmax(
-((queries - keys) * self.w) ** 2 / 2, dim=1) # 形状 (n_query, n_train)
# 使用注意力权重对值进行加权求和得到预测值
# bmm: (批量大小, 1, 键值对个数) × (批量大小, 键值对个数, 1) = (批量大小, 1, 1)
# values的形状为(查询个数,"键-值"对个数)
# 注意力权重:在除批次维以外的第一维增加一维;
# 值:在最后一维增加一个维度
# 然后各自增维后的注意力权重与值 执行批量矩阵乘法,计算完成后重塑形状
return (torch.bmm(self.attention_weights.unsqueeze(1), # (n_query, 1, n_train)
values.unsqueeze(-1)) # (n_query, n_train, 1)
.reshape(-1)) # (n_query, 1, 1) → (n_query,)2.4.3. 训练
将训练数据集 变换为 键和值 用于训练注意力模型。
- 在带参数的注意力汇聚模型中,
- 任何一个训练样本的输入 都会和除自己以外的所有训练样本的"键-值"对进行计算,
- 从而得到其对应的预测输出。
- 即 通过掩码排除自身匹配,强制模型关注其他样本
生成训练数据的所有组合(用于自注意力),即 准备训练时的 keys 和 values
- 将训练数据和标签都:
- 第0维:重复次数为查询数据总数,以便对应每个查询,在前向传播中每个键都能与查询计算差异
- 训练阶段:重复训练数据总数次
- 测试阶段:重复测试数据总数次
- 第1维:原封不动,即 重复一次
- 若是训练阶段,则需通过掩码排除自匹配(排除后第2维的长度会-1,因为少了对角线位置的元素)。若是测试阶段则无需排除自匹配,重复第0维元素后键矩阵和值矩阵即已完成。
python
print(f"x_train.shape={x_train.shape}") # ([50])
print(f"repeat((n_train, 1)).shape={x_train.repeat((n_train, 1)).shape}") # ([50, 50])
# 准备训练时的 keys 和 values (用于自注意力)
# X_tile的形状:(n_train,n_train),每一行都包含着相同的训练输入
# Y_tile的形状:(n_train,n_train),每一行都包含着相同的训练输出
# x_train第0维直接重复x_train次(对应训练数据的个数),第1维重复一次(保持不变)
# 原本x_train是长度为50的向量形状,.repeat后形状变为(训练数据总是, 50)
X_tile = x_train.repeat((n_train, 1)) # 形状 (n_train * n_train, dim)
Y_tile = y_train.repeat((n_train, 1)) # 形状 (n_train * n_train, dim)
# (排除对角线元素,即自身。避免自匹配)
# mask 用于排除自匹配(即查询点不与自身计算注意力)
# 1与对角线为1的单位矩阵做差,再转换为bool类型 (使对角区域为false,以便排除)
mask = (1 - torch.eye(n_train)).type(torch.bool) # 形状 (n_train, n_train)
# 等效于以下两种方法
# mask = ~torch.eye(n_train, dtype=torch.bool) # 方法2:直接创建布尔掩码(更高效)
# mask = (torch.eye(n_train) == 0) # 方法3:使用比较操作
# 创建键和值
# keys的形状 :('n_train','n_train'-1)
# values的形状:('n_train','n_train'-1)
# 通过掩码mask从 _tile中选择元素(每行元素皆少了对角线位置的那个),然后再重新排列(行数不变)
keys = X_tile[mask].reshape((n_train, -1)) # 形状 (n_train, n_train-1)
values = Y_tile[mask].reshape((n_train, -1)) # 形状 (n_train, n_train-1)训练带参数的注意力汇聚模型时,使用平方损失函数和随机梯度下降:
python
# 初始化模型、损失函数和优化器
net = NWKernelRegression()
loss = nn.MSELoss(reduction='none') # 逐元素计算损失
trainer = torch.optim.SGD(net.parameters(), lr=0.5)
animator = common.Animator(xlabel='epoch', ylabel='loss', xlim=[1, 5])
for epoch in range(5):
trainer.zero_grad() # 清零梯度
# 计算每个训练点的预测值(queries=x_train, keys/values来自其他点)
l = loss(net(x_train, keys, values), y_train) # 前向传播
l.sum().backward() # 反向传播(对损失求和后反向传播)
trainer.step() # 更新参数
print(f'epoch {epoch + 1}, loss {float(l.sum()):.6f}')
animator.add(epoch + 1, float(l.sum()))
如下所示,训练完带参数的注意力汇聚模型后可以发现:在尝试拟合带噪声的训练数据时,预测结果绘制的线不如之前非参数模型的平滑。
python
# 测试阶段:每个测试点与所有训练点计算注意力
# keys的形状 :(n_test,n_train),每一行包含着相同的训练输入(例如,相同的键)
# value的形状:(n_test,n_train),每一行都包含相同的训练输出(例如,相同的值)
# x_train第0维元素重复n_test次(对应测试数据的个数),第2维元素重复一次(不变)
# 原本x_train是长度为50的向量形状,.repeat后键和值的形状变为(测试数据总数, 50)
keys = x_train.repeat((n_test, 1)) # 形状 (n_test, n_train)
values = y_train.repeat((n_test, 1)) # 形状 (n_test, n_train)
y_hat = net(x_test, keys, values).unsqueeze(1).detach() # 预测
plot_kernel_reg(y_hat) # 绘制回归结果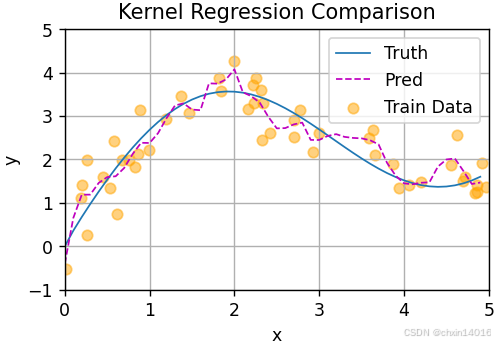
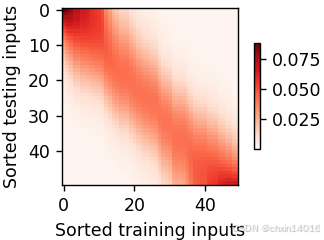
新的模型更不平滑的原因:
- 下面看一下输出结果的绘制图:与非参数的注意力汇聚模型相比,
- 带参数的模型加入可学习的参数后,曲线在注意力权重较大的区域变得更不平滑。
python
# 可视化注意力权重(测试点 vs 训练点)
# net.attention_weights形状: (n_test, n_train)
# 添加两个维度使其变为(1, 1, n_test, n_train)以匹配show_heatmaps期望的4D输入
common.show_heatmaps(
net.attention_weights.unsqueeze(0).unsqueeze(0), # 增加批次和头维度
xlabel='Sorted training inputs',
ylabel='Sorted testing inputs')
plt.pause(4444) # 间隔的秒数: 4s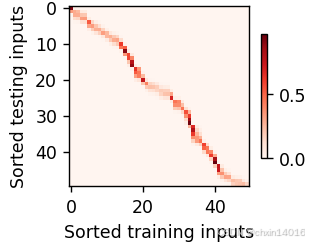
小结
Nadaraya-Watson核回归:是具有注意力机制的机器学习范例。
Nadaraya-Watson核回归的注意力汇聚是对训练数据中输出的加权平均。从注意力的角度来看,分配给每个值的注意力权重取决于将值所对应的键和查询作为输入的函数。
注意力汇聚可以分为:
非参数型 和
带参数型
简单例子描述模型中qkv矩阵的形状变化和元素计算过程
假设训练数据为:
pythonx_train = torch.tensor([1.0, 2.0, 3.0]) # 形状(3,) y_train = torch.tensor([4.0, 5.0, 6.0]) # 形状(3,) n_train = 31)构造keys和values矩阵
步骤分解:
生成
X_tile和Y_tile(通过重复训练数据):
pythonX_tile = x_train.repeat((n_train, 1)) # 形状(3,3) # 结果:[[1,2,3], # [1,2,3], # [1,2,3]] Y_tile = y_train.repeat((n_train, 1)) # 形状(3,3) # 结果:[[4,5,6], # [4,5,6], # [4,5,6]]创建掩码排除自匹配:
pythonmask = (1 - torch.eye(n_train)).type(torch.bool) # 形状(3,3) # 结果:[[False, True, True], # [True, False, True], # [True, True, False]]通过掩码提取非对角线元素:
pythonkeys = X_tile[mask].reshape((n_train, n_train-1)) # 形状(3,2) # 结果:[[ 2,3], # 对应x=1时排除自身 # [1, 3], # 对应x=2时排除自身 # [1,2 ]] # 对应x=3时排除自身 values = Y_tile[mask].reshape((n_train, n_train-1)) # 形状(3,2) # 结果:[[ 5,6], # 对应x=1时排除自身 # [4, 6], # 对应x=2时排除自身 # [4,5 ]] # 对应x=3时排除自身2)查询过程示例(以查询点q=2.0为例)
输入参数:
queries = torch.tensor([2.0])# 形状(1,)keys如上所述(形状(3,2))values如上所述(形状(3,2))
步骤分解:
扩展查询向量形状:
pythonqueries = queries.repeat_interleave(keys.shape[1]).reshape((-1, keys.shape[1])) # 结果:[[2,2]] # 形状(1,2)计算注意力权重:
假设初始
w = 1.0(可学习参数)计算高斯核相似度:
pythondist = (queries - keys) * w # 形状(1,3,2) # 具体计算: # queries-keys = [[2-2, 2-3], # 第一行对应keys[0] # [2-1, 2-3], # 第二行对应keys[1] # [2-1, 2-2]] # 第三行对应keys[2] # = [[0,-1], # [1,-1], # [1,0]] squared_dist = dist**2 # 形状(1,3,2) # 结果:[[0,1], # [1,1], # [1,0]] attention_scores = -squared_dist / 2 # 高斯核公式 # 结果:[[0, -0.5], # [-0.5, -0.5], # [-0.5, 0]] attention_weights = nn.functional.softmax(attention_scores, dim=1) # 结果(近似): # 第一行:[0.622, 0.378] # softmax([0,-0.5]) # 第二行:[0.378, 0.622] # softmax([-0.5,-0.5]) # 第三行:[0.622, 0.378] # softmax([-0.5,0])加权求和得到预测值 :
pythonoutput = torch.bmm(attention_weights.unsqueeze(1), values.unsqueeze(-1)).reshape(-1) # 具体计算: # 第一行:0.622*5 + 0.378*6 ≈ 5.378 # 第二行:0.378*4 + 0.622*6 ≈ 5.124 # 第三行:0.622*4 + 0.378*5 ≈ 4.378 # 最终输出形状(1,) → [14.88]3)形状变化总结
矩阵 初始形状 中间形状 最终用途 queries(n_query,) (n_query, n_train-1) (排除自身) 扩展后与keys对齐计算距离 keys(n_train, n_train-1) 保持不变 存储非自身键值 values(n_train, n_train-1) 保持不变 存储非自身值 注意力权重 - (n_query, n_train-1) (排除自身) 对值进行加权 输出 - (n_query,) 加权求和结果
3. 注意力评分函数
(2. 注意力汇聚:Nadaraya-Watson 核回归)使用了高斯核来对查询和键之间的关系建模。
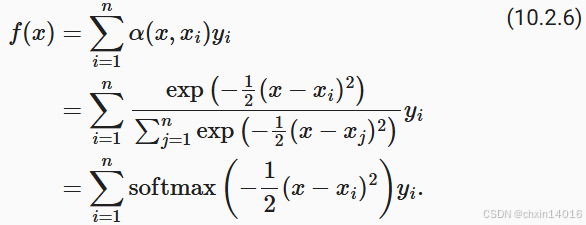 基于高斯核注意力机制
基于高斯核注意力机制
注意力评分函数 (attention scoring function),简称评分函数(scoring function):
- 例如(10.2.6)中的 高斯核指数部分;
- 使用过程:
- 高斯核指数运算后,然后把该评分函数的输出结果 输入到softmax函数中进行运算。
- 通过上述步骤,将得到与键对应的值的概率分布(即注意力权重)。
- 最后,注意力汇聚的输出就是基于这些注意力权重的值的加权和。
从宏观来看,上述算法可以用来实现 图10.1.3中的注意力机制框架。
 图10.1.3 注意力机制通过 注意力汇聚
图10.1.3 注意力机制通过 注意力汇聚
将 查询 (自主性提示)和 键 (非自主性提示)结合在一起,
实现对 值(感官输入)的选择倾向
图10.3.1说明了 如何将注意力汇聚的输出计算成为值的加权和,其中a表示注意力评分函数。由于注意力权重是概率分布,因此加权和其本质上是加权平均值。
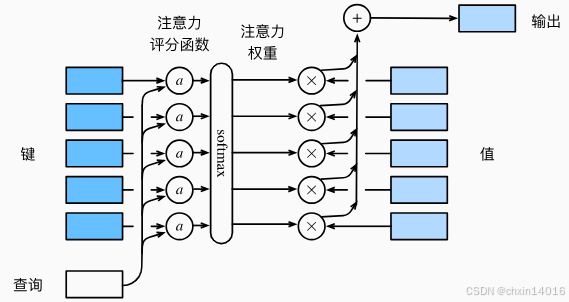 图10.3.1 计算注意力汇聚的输出为值的加权和
图10.3.1 计算注意力汇聚的输出为值的加权和
用数学语言描述,假设有
- 一个查询
和
个"键-值"对
,
- 其中
,
。
- 其中
- 注意力汇聚函数
就被表示成值的加权和:
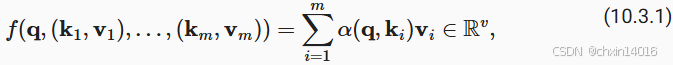
其中 查询 和 键
的注意力权重(标量),是通过注意力评分函数a将两个向量映射成标量,再经过softmax运算得到的:
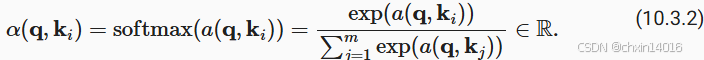
正如上图所示,选择不同的注意力评分函数a会导致不同的注意力汇聚操作。本节将介绍两个流行的评分函数,稍后将用他们来实现更复杂的注意力机制。
python
import math
import torch
from torch import nn
import common3.1. 掩蔽softmax操作
softmax操作:用于输出一个概率分布作为注意力权重。
- 在某些情况下,并非所有的值都应该被纳入到注意力汇聚中。
- 例如, 在(现代循环神经网络------动手学深度学习9-CSDN博客中的 5. 机器翻译与数据集)中
- 某些文本序列会填充没有意义的特殊词元,以便高效处理小批量数据集。
- 为了仅将有意义的词元作为值来获取注意力汇聚,可以指定一个有效序列长度(即词元的个数),以便在计算softmax时过滤掉超出指定范围的位置。
masked_softmax函数:实现了如上的掩蔽softmax操作(masked softmax operation),
- 其中任何超出有效长度的位置都被掩蔽并置为0。
python
def masked_softmax(X, valid_lens):
"""带掩码的softmax函数,用于处理变长序列:通过在最后一个轴上掩蔽元素来执行softmax操作
掩膜后,则只保留了每个序列中有效的特征维度(无效的都变为0)
X : 3D张量,待掩膜的矩阵,
形状为 (批次batch_size, 序列长度seq_length, 特征维度feature_dim)
valid_lens: 每个样本的有效长度(非填充位置),1D或2D张量
- None: 不使用掩码
- 1D: 每个序列的有效长度
- 2D: 每个序列中每个位置的有效长度
返回: 经过掩蔽处理的softmax结果,形状与X相同
"""
if valid_lens is None: # 没有提供有效长度,则直接执行标准softmax
return nn.functional.softmax(X, dim=-1) # dim=-1是沿最后一维进行softmax归一化
else:
shape = X.shape # 张量形状
if valid_lens.dim() == 1:
# 当valid_lens是1D时:扩展为与X第二维匹配
# 如 batch_size=2, seq_length=3,valid_lens=[2,1] (两个序列的有效长度分别为2和1)
# -> 扩展为 [len1, len1, len1, len2, len2, len2],即 [2,2,2,1,1,1]
# 输入的有效长度为1维,每个元素对应原矩阵中每个序列(每行)的有效长度
# 因此将有效长度向量中,每个元素重复,重复次数对应每批次的序列数量(原矩阵的第1维)
valid_lens = torch.repeat_interleave(valid_lens, shape[1])
else:
# 当valid_lens是2D时:展平为一维张量
# 因为有效长度为2d时,就是已经细分了每个序列自己的有效长度,因此直接展平即可
# 例如valid_lens = [[2, 2, 1], [1, 0, 0]](每个序列中每个位置的有效长度)
# - 展平后: [2, 2, 1, 1, 0, 0]
valid_lens = valid_lens.reshape(-1)
# 核心掩蔽操作:
# 1. X.reshape(-1, shape[-1])将X重塑为二维张量(batch_size * seq_length, feature_dim)
# 2. 使用sequence_mask生成掩码:
# - 有效位置保持原值
# - 无效位置(超出有效长度的位置)被替换为 -1e6(极大负值)
# 3. 经过softmax后,无效位置输出概率接近0
# 最后一轴上被掩蔽的元素使用一个非常大的负值替换,从而其softmax输出为0
X = sequence_mask(X.reshape(-1, shape[-1]), valid_lens,
value=-1e6)
# 恢复原始形状并执行softmax
return nn.functional.softmax(X.reshape(shape), dim=-1)演示:已有两个2×4矩阵表示的样本,其有效长度分别为2和3。经过掩蔽softmax操作,超出有效长度的值都被掩蔽为0。
python
print(f"两个有效长度分别为2和3的 2×4矩阵,经过掩蔽softmax操作后结果:\n"
f"{common.masked_softmax(torch.rand(2, 2, 4), torch.tensor([2, 3]))}")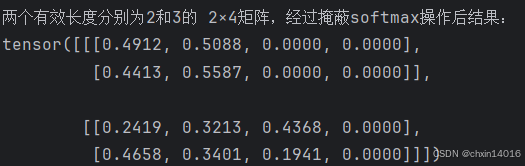
同样,也可以使用二维张量,为矩阵样本中的每一行指定有效长度:
python
print(f"以二维张量作为输入指定每行的有效长度:\n"
f"{common.masked_softmax(torch.rand(2, 2, 4), torch.tensor([[1, 3], [2, 4]]))}")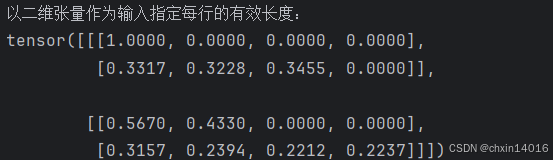
3.2. 加性注意力(适用于查询和键维度不同的情况)
- 查询和键 映射到同一空间(转成相同维度)后,
- 再相加结合(广播求和)成为特征,
- 再掩码软分类成为注意力权重,
- 再对值进行加权求和得到预测值。
- 注意力机制的核心 是找差异 或相关性,
- 但 加性注意力 的实现方式不是直接计算差异,而是 通过一种**"融合"**方式来衡量相关性。
- 即 加性注意力 核心思想 :不是计算差异,而是构建联合表征 。
- 要判断查询(Query)和键(Key)是否相关,不是看相差多少,而是看融合后的联合表征是否显著。
直接差异的局限性:
直接计算
query - key只能捕捉到两者之间的绝对距离。但很多情况下,即使两个向量相距很远,只要它们在某个子空间中有相似的"模式",就可能是高度相关的。
融合的优势:
query + key的融合操作实际上是在构建一个联合特征空间。这个融合后的向量包含了查询和键的所有信息。
在运算步骤中:
融合而非比较
queries + keys不是计算距离,而是创建每个查询-键对的联合表征这个联合表征捕捉了"如果查询和键同时存在,会是什么样子"
非线性评估
tanh函数评估这个联合表征的"质量"或"显著性"权重向量
v然后学习哪些联合表征特征对于判断相关性最重要想象要判断两本书的相关性:
差异方法:比较两本书的目录,看有多少相同的条目(直接比较)
加性方法:将两本书的内容融合,看这个融合后的"超级书"是否有意义、连贯(融合评估)
加性注意力采用第二种思路:如果查询和键是相关的,它们的融合应该产生一个有意义的、连贯的表征。
总结
加性注意力使用相加融合+非线性变换而不是直接计算差异,是因为:
融合比差异更能捕捉复杂的相关性模式
非线性变换允许学习任意的决策边界
这种设计提供了更强的表达能力和灵活性
从数学上看,这等价于对拼接向量的神经网络处理
加性注意力 核心思想 :
- 通过学习一个小型神经网络,将不同维度的查询和键映射到同一个空间,
- 然后在该空间中 进行相似度计算,从而得到注意力权重。
适用场景:查询和键是不同长度的矢量时,即 维度不同时。
当查询和键是不同长度的矢量时,可以使用【加性注意力】作为评分函数。
- 给定 查询
和 键
,加性注意力(additive attention)的评分函数为:
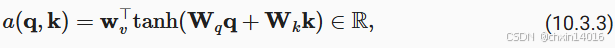
- 其中可学习的参数是
、
和
。
如 (10.3.3)所示,将查询和键连结起来后输入到一个多层感知机(MLP)中,感知机包含一个隐藏层,其隐藏单元数是一个超参数。 通过使用
作为激活函数,并且禁用偏置项。
下面实现加性注意力:
python
class AdditiveAttention(nn.Module):
""" 加性注意力机制(Additive Attention/ Bahdanau Attention)
通过全连接层和tanh激活计算注意力分数,适用于查询和键维度不同的情况
这里的类成员变量说的维度皆是指特征维度
key_size : 键向量的维度
query_size : 查询向量的维度
num_hiddens : 隐藏层大小(注意力计算中间层的维度)
dropout : dropout比率
kwargs : 其他传递给父类的参数
加性注意力通过将查询和键映射到同一空间并相加,然后通过一个单层前馈网络计算注意力分数
自己理解:
就是这个工具人小型神经网络中,只有一个隐藏层(全连接层)(用于转相同维度),和一个输出层(用于转单个标量)
键和查询皆通过这个神经网络,经隐藏层后映射到相同维度,然后再结合,再经过线性层映射为标量,得到权重值
结合方式是 广播求和再经过非线性函数tanh。
得到注意力权重后,再经过随机失活层再与值做批量矩阵乘法得到预测值。
"""
def __init__(self, key_size, query_size, num_hiddens, dropout, **kwargs):
super(AdditiveAttention, self).__init__(**kwargs)
# 将键和查询映射到相同隐藏空间的全连接层
self.W_k = nn.Linear(key_size, num_hiddens, bias=False) # 键变换矩阵
self.W_q = nn.Linear(query_size, num_hiddens, bias=False) # 查询变换矩阵
# 将隐藏状态映射到标量分数的线性变换
# 输出单分数值的全连接层(相当于注意力权重向量)
self.w_v = nn.Linear(num_hiddens, 1, bias=False) # 分数计算层
self.dropout = nn.Dropout(dropout) # 注意力权重dropout,防止过拟合
def forward(self, queries, keys, values, valid_lens):
'''
queries : 查询向量 [batch_size, 查询个数num_queries, query_size]
keys : 键向量 [batch_size, 键值对个数num_kv_pairs, key_size]
values : 值向量 [batch_size, 键值对个数num_kv_pairs, value_size]
valid_lens : 有效长度 [batch_size,] 或 [batch_size, num_queries] 用于掩码处理
返回:注意力加权后的值向量 [batch_size, num_queries, value_size]
'''
# 投影变换:将查询和键映射到相同维度的隐藏空间
queries, keys = self.W_q(queries), self.W_k(keys) # 形状变为 [batch_size, *, num_hiddens]
# (核心步骤)
# 以便进行广播相加,在维度扩展后:
# queries 添加中间维度 -> [batch_size, num_queries, 1, num_hiddens]
# keys 添加第二维度 -> [batch_size, 1, num_kv_pairs, num_hiddens]
# queries的形状:(batch_size,查询的个数,1,num_hidden)
# key的形状:(batch_size,1,"键-值"对的个数,num_hiddens)
# 广播方式求和,使每个查询与所有键相加,
# 自动扩展为 [batch_size, 查询数num_queries, 键值对数num_kv_pairs, num_hiddens]
features = queries.unsqueeze(2) + keys.unsqueeze(1) # 创建每个查询-键对的联合表征
features = torch.tanh(features) # 非线性变换(原始论文使用tanh),保持形状不变
# 通过线性层计算注意力分数(原始论文的a(s,h)计算)
# 通过w_v将特征映射为标量分数 -> [batch_size, num_queries, num_kv_pairs, 1]
# 移除最后一个维度 -> [batch_size, num_queries, num_kv_pairs]
# self.w_v仅有一个输出,因此从形状中移除最后那个维度
# scores的形状:(batch_size,查询的个数,"键-值"对的个数)
scores = self.w_v(features).squeeze(-1) # 将特征映射为一个标量
# 应用掩码softmax获取归一化注意力权重
# 只保留有效位置的数据然后进行归一化
self.attention_weights = masked_softmax(scores, valid_lens)
# 注意力对值进行加权求和(使用dropout正则化)
# torch.bmm批矩阵乘法:
# [batch_size, num_queries, num_kv_pairs] × [batch_size, num_kv_pairs, value_size]
# 结果形状 -> [batch_size, num_queries, value_size]
# values的形状:(batch_size,"键-值"对的个数,值的维度)
return torch.bmm(self.dropout(self.attention_weights), values)用个小例子来演示上面的AdditiveAttention类,其中
- 查询、键和值的形状为(批量大小,步数或词元序列长度,特征大小)
- 实际输出 为 (2, 1, 20)、 (2, 10, 2) 和 (2, 10, 4)
- 注意力汇聚输出的形状为(批量大小,查询的步数,值的维度)
python
# 创建测试数据
# 查询、键和值的形状为(批量大小,步数或词元序列长度,特征大小)
# 实际输出 为 q(2, 1, 20)、 k(2, 10, 2)、 v(2, 10, 4)
# 从均值为0,标准差为1的正态分布中随机抽取值来初始化查询q,键k初始化为全0
queries, keys = torch.normal(0, 1, (2, 1, 20)), torch.ones((2, 10, 2))
# values的小批量,两个值矩阵是相同的
values = torch.arange(40, dtype=torch.float32).reshape(1, 10, 4).repeat(2, 1, 1)
valid_lens = torch.tensor([2, 6]) # 两个批量的有效长度分别为2和6
# 注意力汇聚输出的形状为(批量大小,查询的步数,值的维度)
# 将特征维度q20与k2映射到同一空间hidden8,再广播
attention = common.AdditiveAttention( # 初始化加性注意力层
key_size =2, # 键向量维度(与keys的最后一维匹配)
query_size =20, # 查询向量维度(与queries的最后一维匹配)
num_hiddens =8, # 隐藏层大小(注意力计算空间维度)
dropout =0.1) # 注意力权重随机丢弃率
attention.eval() # 设置为评估模式(关闭dropout)
output = attention(queries, keys, values, valid_lens)
print(f"加性注意力输出结果:\n{output}")
尽管加性注意力包含了可学习的参数,但由于本例中每个键皆相同,所以注意力权重是均匀的,由指定的有效长度决定。
python
common.show_heatmaps(attention.attention_weights.reshape((1, 1, 2, 10)),
xlabel='Keys', ylabel='Queries')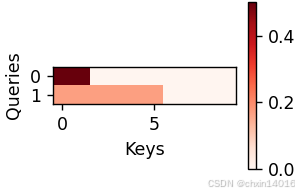
3.3. 缩放点积注意力
- 对每个查询向量和键向量计算点集分数(即查询和键的相似度)
- 计算点积时用缩放因子稳定训练过程,
- 再对前面得到的点积分数 掩码软分类成为注意力权重,
- 再对值进行加权求和得到预测值。
直接计算向量积(点积)的本质 是衡量两个向量的方向相似性:
当两个向量方向完全一致 时,点积最大
当两个向量方向正交 时 ,点积为零 (方向正交,即两向量互相垂直)
这完美契合"注意力"的直觉:相关性越高,关注度越高
总结:
正交 = 垂直 = 点积为零
表示两个向量方向完全不相关
在注意力机制中,正交意味着"不关注"
核心思想 :
- 使用矩阵乘法(点积)直接计算查询(Query)和键(Key)的相似度,
- 并通过一个缩放因子来稳定训练过程。
缩放点积注意力是对原始点积注意力的一个改进(增加缩放) 。其设计目标是:
极致的计算效率:利用高度优化的矩阵乘法操作,计算速度远快于加性注意力。
解决原始点积的问题:原始点积在维度较高时,结果方差较大,导致Softmax后的梯度非常小(饱和区),需要通过缩放来缓解。
- 使用点积可以得到计算效率更高的评分函数,但点积操作要求查询和键具有相同的长度
。
- 假设查询和键的所有元素都是独立的随机变量,且都满足零均值和单位方差,那么两个向量的点积的均值为0,方差为
。
- 为确保无论向量长度如何,点积的方差在不考虑向量长度的情况下仍然是1,我们再将点积除以
,则 缩放点积注意力(scaled dot-product attention)评分函数为:

(10.3.4)公式指的是向量形式 👆

在实践中,通常从小批量的角度来考虑提高效率,例如
- 基于n个查询 和 m个键-值对计算注意力,
- 其中 查询和键的长度为d,值的长度为
。
- 查询
、 键
和 值
的缩放点积注意力是:
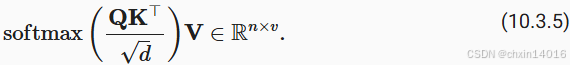
:查询矩阵(Query),形状为
(..., seq_len_q, d_k):键矩阵(Key) ,形状为
(..., seq_len_k, d_k):值矩阵(Value) ,形状为
(..., seq_len_v, d_v):键和查询的维度(dimension of key)
:缩放因子(Scaling Factor),这是其与原始点积注意力的唯一区别。
给定矩阵 Q, K, V,计算过程如下:(三步走)
计算点积分数(MatMul):
计算 Q 和 K 的转置的矩阵乘法:
。
作用 :得到一个注意力分数矩阵,其中的每个元素
score[i, j]表示第i个查询与第j个键的相似度。形状为(..., seq_len_q, seq_len_k)。代码 :
scores = torch.matmul(Q, K.transpose(-2, -1))缩放与应用Softmax(Scale & Softmax):
缩放 :将分数矩阵除以
。
作用 :假设查询和键是均值为0、方差为1的独立随机变量,则它们的点积的均值是0,方差是
。缩放后方差重新变为1,防止点积结果进入Softmax函数的梯度极小区域(饱和区),从而缓解梯度消失问题,使训练更稳定。
Softmax :对缩放后的分数矩阵在最后一个维度(
seq_len_k)上进行Softmax归一化,得到注意力权重矩阵,所有权重和为1。代码 :
weights = F.softmax(scores / math.sqrt(d_k), dim=-1)加权求和(MatMul):
将上一步得到的注意力权重矩阵与值矩阵V相乘。
作用 :对所有的值向量进行加权求和,输出最终的注意力输出。形状为
(..., seq_len_q, d_v)。代码 :
output = torch.matmul(weights, V)
需要缩放的原因(Scaling的核心原因):
(理解缩放点积注意力的关键)
原始点积的问题 :点积
的结果的数值范围会随着维度
的增大而变得非常大。
Softmax的特性:Softmax函数对非常大的输入值非常敏感。当某个值远大于其他值时,它的输出会非常接近1(其他接近0),梯度会变得非常小(进入饱和区)。
scaled :除以
可以将点积结果的方差重新缩放回1,确保无论
多大,Softmax的输入都处于一个合理的范围,从而保持梯度稳定,加速模型收敛。
简单比喻 :就像给过热发动机加一个冷却系统,
就是这个冷却剂,确保发动机(Softmax)不会因为温度过高(数值过大)而停止工作(梯度消失)。
下面的缩放点积注意力的实现使用了暂退法进行模型正则化:
python
class DotProductAttention(nn.Module):
""" 缩放点积注意力(Scaled Dot-Product Attention)
通过点积计算查询和键的相似度,并用缩放因子稳定训练过程
dropout: 注意力权重的随机失活率
"""
def __init__(self, dropout, **kwargs):
super(DotProductAttention, self).__init__(**kwargs)
self.dropout = nn.Dropout(dropout) # 初始化随机失活层
def forward(self, queries, keys, values, valid_lens=None):
'''
queries : (batch_size,查询的个数,d)
keys : (batch_size,"键-值"对的个数,d)
values : (batch_size,"键-值"对的个数,值的维度)
valid_lens: (batch_size,)或(batch_size,查询的个数)
return:注意力加权后的值向量 [batch_size, num_queries, value_dim]
'''
d = queries.shape[-1] # 获取查询和键的特征维度d(用于缩放)
# 1:计算点积分数(原始注意力分数)
# 设置transpose_b=True为了交换keys的最后两个维度
# keys.transpose(1,2):将键的最后两维转置,即 从(b,nk,d)变为(b,d,nk)
# 数学等价:对每个查询向量q和键向量k计算q·k^T 即 q乘以k的转置
# 缩放因子:/ math.sqrt(d)防止高维点积数值过大,避免梯度消失
# 矩阵乘法:查询q形状(b,nq,d) × k转置形状(b,d,nk) → 点积分数scores形状(b,nq,nk)
scores = torch.bmm(queries, keys.transpose(1,2)) / math.sqrt(d)
# 2:应用掩码softmax归一化
# 根据有效长度屏蔽无效位置,并归一化得到注意力权重
self.attention_weights = masked_softmax(scores, valid_lens)
# 3:注意力权重与值向量加权求和
# 注意力权重(在训练时会随机失活)与值做批量矩阵乘法
# 矩阵乘法:weights形状(b,nq,nk) × values形状(b,nk,vd) → 输出形状(b,nq,vd)
return torch.bmm(self.dropout(self.attention_weights), values)为了演示上述的DotProductAttention类,下面使用与先前加性注意力例子中相同的键、值和有效长度。对于点积操作,令查询的特征维度与键的特征维度大小相同:
python
# 查询从均值为0,标准差为1的正态分布中随机抽取指来初始化
# 批次为2即两个样本,每个样本1个查询即1个序列,序列特征即查询的特征维度为2(与键的特征维度相同)
queries = torch.normal(0, 1, (2, 1, 2))
# 训练时会随机丢弃50%的注意力权重(当前eval模式关闭)
attention = common.DotProductAttention(dropout=0.5) # 初始化放缩点积注意力层
attention.eval() # 设置为评估模式(关闭dropout等训练专用操作)
output = attention(queries, keys, values, valid_lens) # 前向传播计算
print(f"放缩点积注意力输出结果:\n{output}")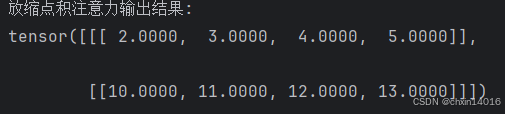
与加性注意力演示相同,由于键包含的是相同的元素,而这些元素无法通过任何查询进行区分,因此获得了均匀的注意力权重。
python
common.show_heatmaps(attention.attention_weights.reshape((1, 1, 2, 10)),
xlabel='Keys', ylabel='Queries')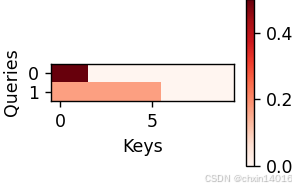
加性注意力 vs. 缩放点积注意力
| 特性 | 加性注意力 (Additive Attention) | 缩放点积注意力 (Scaled Dot-Product) |
|---|---|---|
| 核心计算 | 单层前馈网络 + tanh | 矩阵乘法(点积)+ 缩放 |
| 适用场景 | 查询和键的维度不同时,更灵活 | 查询和键的维度相同 ( |
| 计算复杂度 | 较高 ( |
较低 ( |
| 空间复杂度 | 需要存储巨大的注意力分数矩阵 | 类似 |
| 表达能力 | 较强(有非线性激活) | 较弱(线性变换) |
| 参数数量 | 较多(需要映射矩阵) | 较少(直接计算) |
| 代表模型 | 早期RNN-based的Seq2Seq模型, Bahdanau 注意力(原始论文) | Transformer, BERT, GPT 等几乎所有现代模型 |
| 缩放 | 通常不需要 | 需要缩放(Scaled)以防止梯度消失 |
小结
将注意力汇聚的输出计算可以作为值的加权平均,选择不同的注意力评分函数会带来不同的注意力汇聚操作。
当查询和键为不同长度的矢量时,可以使用可加性注意力评分函数。
当它们的长度相同时,使用缩放的"点-积"注意力评分函数的计算效率更高。
4. Bahdanau 注意力 (带注意力机制的编码器-解码器模型)
-
与传统Seq2Seq 的差异:将固定的同一个上下文变量
换成 每个时间步单独的
。
-
是编码器所有隐藏状态的加权和,权重由当前解码器状态与所有编码器状态的相关性决定。
python# 通过动态计算源序列各位置权重,使解码器在生成每个词时聚焦于源序列的相关部分 # 核心公式: context = ∑(attention_weights * enc_outputs) # 上下文向量 = 加权和其中注意力权重由 查询向量(解码器隐藏状态) 与 编码器输出(键/值) 的相似度决定。
实现逻辑:直接将序列到序列学习的编码器不变,解码器稍作修改:
- init_state 将编码器输出预处理好(调整 编码器所有时间步隐状态 的维度)
- 改所有时间步隐状态的维度:编码器出来是批次在前→改成GRU所需的步次在前(批次与步次调换位置)
- 前向传播:
- 解包传入的 处理好的编码器输出(编码器所有时间步隐状态、编码器最终隐状态、有效长度)
- 将输入X词嵌入(将词元ID转为向量)并调整维度
- 开始逐时间步处理(解码)
- 取出最后一层隐状态并处理(在第0维插入一个维度以匹配)后作为 查询
- 编码器所有时间步的隐状态作为 键 和 值
- qkv通过加性注意力(联合表征)得到 注意力权重(qk联合表征得到) 和 上下文变量(注意力权重与v加权求和计算得出)
- 上下文变量 与 当前词嵌入 拼接
- 拼接结果送入GRU门控循环单元,得到 输出与最后层隐状态 (在此步动态更新)
- 存数当前时间步的 输出 和 注意力权重
- 将所有输出映射回词表空间,即为最终预测结果语句。
(现代循环神经网络------动手学深度学习9-CSDN博客中的7. 序列到序列学习(seq2seq)) 中探讨了机器翻译问题:通过设计一个基于两个循环神经网络的编码器-解码器架构,用于序列到序列学习。具体来说,
- 循环神经网络编码器 将长度可变 的序列转换为固定形状的上下文变量,
- 然后循环神经网络解码器 根据生成的词元和上下文变量 按词元生成输出(目标)序列词元。
然而,即使并非所有输入(源)词元都对解码某个词元都有用, 在每个解码步骤中仍使用编码相同的上下文变量。 有什么方法能改变上下文变量呢?
- 解决的问题 :
- 在传统的编码器-解码器(Seq2Seq)模型中,解码器在每个时间步都使用同一个上下文向量(即编码器最后一个隐藏状态)。
- 这导致了一个瓶颈:无论当前要生成哪个目标词,模型都只能访问源序列的固定长度、压缩后的表示,无法动态 地关注与当前生成词最相关的源词。
我们试着从 (Graves, 2013)中找到灵感: 在为给定文本序列生成手写的挑战中, Graves设计了一种可微注意力模型, 将文本字符与更长的笔迹对齐, 其中对齐方式仅向一个方向移动。 受学习对齐想法的启发,Bahdanau等人提出了一个没有严格单向对齐限制的 可微注意力模型 (Bahdanau et al., 2014)。 在预测词元时,如果不是所有输入词元都相关,模型将仅对齐(或参与)输入序列中与当前预测相关的部分。这是通过将上下文变量视为注意力集中的输出来实现的。
- 核心创新 :
- Bahdanau 注意力不再使用单一的固定上下文向量。
- 相反,它在解码器的每一个时间步 都动态地生成一个新的、独特的上下文向量
。
- 这个
是编码器所有隐藏状态的加权和,权重由当前解码器状态与所有编码器状态的相关性决定。
- 核心目标:让模型学会"对齐"或"关注"输入序列中与当前输出词最相关的部分,从而实现更精准的翻译或生成。
4.1. 模型
(9.7节):(现代循环神经网络------动手学深度学习9-CSDN博客中的7. 序列到序列学习(seq2seq))
- 下面描述的Bahdanau注意力模型 将遵循 (9.7节) 中的相同符号表达。
- 这个新的基于注意力的模型
- 与 (9.7节) 中的模型相同,
- 只不过 (9.7.3)
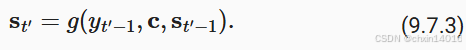 中的上下文变量
中的上下文变量在任何解码时间步
都会被
替换。
- 假设输入序列中有
个词元,解码时间步
的上下文变量是注意力集中的输出:

其中,时间步时的解码器隐状态
是查询, 编码器隐状态
既是键,也是值, 注意力权重
是使用 (10.3.2) 所定义的加性注意力打分函数计算的。
与 图9.7.2中的循环神经网络编码器-解码器架构略有不同, 图10.4.1描述了Bahdanau注意力的架构。
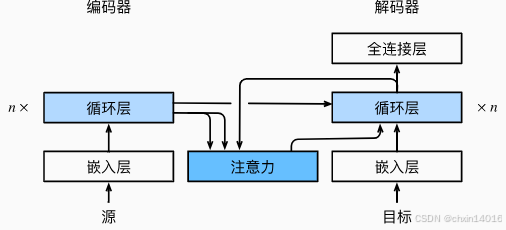 图10.4.1 一个带有Bahdanau注意力的 循环神经网络编码器-解码器模型
图10.4.1 一个带有Bahdanau注意力的 循环神经网络编码器-解码器模型
- 编码器循环层产生的
- 所有时间步的隐状态:作为键和值 用于生成 每一时间步的注意力权重
- 最后一层的隐状态:作为首次的查询 用于生成 首个时间步的注意力权重
- 每一时间步的注意力产生的:
- 注意力权重:(由查询结合键得到,如 加性注意力是查询与键直接相加,即联合表征)用于计算上下文变量,并存储
- 上下文变量:(注意力与值加权求和得到) 给到解码器的循环层里,用于与当前时间步的词嵌入拼接,并存储
- 解码器的循环层产生:
- 第二次及之后动态更新的最后层隐状态:作为查询 用于生成 第二个及之后时间步的注意力权重
- (解码器在每个时间步都会用当前最新的最后层隐状态 作为查询)
python
import torch
from torch import nn
from common4.2. 定义注意力解码器
下面定义Bahdanau注意力,实现循环神经网络编码器-解码器。
- 只需重新定义解码器即可。
- 以下
AttentionDecoder类定义了带有注意力机制解码器的基本接口,以便更方便地显示学习的注意力权重。
python
class AttentionDecoder(Decoder):
"""带有注意力机制解码器的基本接口"""
def __init__(self, **kwargs):
super(AttentionDecoder, self).__init__(**kwargs)
@property
def attention_weights(self):
"""注意力权重属性,
子类必须实现此方法
以返回注意力权重(可视化对齐关系)"""
raise NotImplementedError # 强制子类必须实现此方法接下来,在Seq2SeqAttentionDecoder类中 实现带有Bahdanau注意力的循环神经网络解码器:
- 首先,初始化解码器的状态,需要下面的输入:
- outputs:编码器在所有时间步的最终层隐状态,将作为注意力的键和值;
- hidden_state:上一时间步的编码器全层隐状态,将作为初始化解码器的隐状态;
- enc_valid_lens:编码器有效长度(排除在注意力池中填充词元)。
- 在每个解码时间步骤中,
- 解码器上一个时间步的最终层隐状态将用作查询。
- 因此,注意力输出和输入嵌入都连结为循环神经网络解码器的输入。
python
class Seq2SeqAttentionDecoder(AttentionDecoder):
""" 带有注意力机制的 序列到序列解码器 """
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
dropout=0, **kwargs):
""" 初始化注意力解码器
vocab_size : 词汇表大小
embed_size : 词嵌入维度 (每个数据被表示为的向量维度)
num_hiddens: 隐藏层维度 (单个隐藏层的神经元数量)
num_layers : RNN层数 (隐藏层的堆叠次数)
dropout : 随机失活率
"""
super(Seq2SeqAttentionDecoder, self).__init__(**kwargs)
# 加性注意力模块:查询/键/值 的维度均为num_hiddens
# 实现相似度计算与权重分配
self.attention = AdditiveAttention(
num_hiddens, # 查询向量维度
num_hiddens, # 键向量维度
num_hiddens, # 值向量维度
dropout) # 实现Bahdanau的加性注意力机制 (通过联合表征得到注意力权重)
# 词嵌入层:将词元ID映射为向量 (将词元映射为指定维度的向量)
self.embedding = nn.Embedding(vocab_size, embed_size) #(词元ID → 向量)
# GRU(门控循环单元)循环神经网络层(输入=词嵌入+上下文向量,输出隐藏状态)
# 体现注意力对解码的引导
self.rnn = nn.GRU(
embed_size + num_hiddens, # 输入维度为 词嵌入+上下文向量 即 当前输入和上下文变量
num_hiddens, # 隐藏层维度
num_layers, # 堆叠层数
dropout=dropout) #(输入=词嵌入+上下文向量)
# 输出全连接层:将隐藏状态(RNN输出)映射回 词汇表空间(词汇表维度)
self.dense = nn.Linear(num_hiddens, vocab_size) # (隐藏状态→词表概率分布)
def init_state(self, enc_outputs, enc_valid_lens, *args):
''' 处理编码器输出,准备解码器初始状态
enc_outputs: 编码器的输出(所有时间步的隐状态outputs, 最后一层的最终隐状态hidden_state)
即(batch_size, num_steps, num_hiddens)
enc_valid_lens:编码器有效长度 (batch_size,)
返回:解码器初始状态,三元组 (编码器输出、隐藏状态、有效长度)
outputs:编码器所有时间步的隐藏状态(用于注意力计算)(已转置,将时间步防御第0维上)
hidden_state:编码器最终隐藏状态(解码器初始状态)
enc_valid_lens:源序列的有效长度(掩码处理用)
'''
# outputs 形状(batch_size,num_steps ,num_hiddens)(PyTorch的GRU默认输出格式)
# hidden_state形状(num_layers,batch_size,num_hiddens)
outputs, hidden_state = enc_outputs
# .permute(1,0,2)调整outputs维度为(num_steps, batch_size, num_hiddens)
return (outputs.permute(1, 0, 2), hidden_state, enc_valid_lens)
def forward(self, X, state):
'''
X: 输入序列,形状为(batch_size, num_steps)
state: 解码器状态,即 初始状态三元组 (enc_outputs, hidden_state, enc_valid_lens)
返回:
outputs: 输出序列,形状为(batch_size, num_steps, vocab_size)
state: 更新后的状态
'''
# 解包状态:编码器输出、编码器最终隐藏状态、有效长度
# enc_outputs 形状(batch_size,num_steps ,num_hiddens)
# hidden_state形状(num_layers,batch_size,num_hiddens)
enc_outputs, hidden_state, enc_valid_lens = state
# 词嵌入(将输入词元ID转换为向量)
# 并调整维度顺序:(batch_size, num_steps, embed_size)→(num_steps, batch_size, embed_size)
# .permute(1, 0, 2)将第0维和第1维的内容交换位置
X = self.embedding(X).permute(1, 0, 2) # 输出X的形状(num_steps,batch_size,embed_size)
outputs, self._attention_weights = [], [] # 存储输出和注意力权重
for x in X: # 逐时间步处理(解码)
# 当前隐状态作为查询:首次为编码器中最后一层最终隐状态,后续会动态更新,始终指向最后一层的当前隐状态
# hidden_state[-1]取解码器最后一个隐藏层状态(最顶层GRU的输出)
# 取出后 .unsqueeze()在这个最后的隐状态的 第1维位置插入一个大小为1的维度
query = torch.unsqueeze(hidden_state[-1], dim=1) # 形状(batch_size,1,num_hiddens)
# 计算上下文向量(Bahdanau注意力的核心)
# 通过加性注意力计算,权重由 query和编码器状态 enc_outputs决定
context = self.attention( # 形状(batch_size,1,num_hiddens)
query, # 查询向量
enc_outputs, # 编码器所有时间步的输出
enc_outputs, # 作为键和值
enc_valid_lens # 有效长度
) # (通过联合表征得到注意力权重)
# 在特征维度上连结 (拼接 上下文向量和当前词嵌入)
x = torch.cat((context, torch.unsqueeze(x, dim=1)), dim=-1)
# 调整维度并输入RNN(输入rnn目的是通过递归计算来动态更新隐状态)
# 通过GRU处理:将上下文向量与当前词嵌入拼接后输入GRU
# 输入形状 (1, batch_size, embed_size+num_hiddens)
# .permute(1, 0, 2) 将x变形为(1, batch_size, embed_size+num_hiddens)
# PyTorch的RNN/GRU层要求输入张量形状必须为(seq_len, batch_size, 每个时间步输入的特征维度input_size)
out, hidden_state = self.rnn(x.permute(1, 0, 2), hidden_state) # hidden_state动态更新
outputs.append(out) # 存储输出
# 存储当前时间步的注意力权重
self._attention_weights.append(self.attention.attention_weights)
# 合并所有时间步的输出并投影到词表空间
# .cat()从列表中的多个(1,batch_size,num_hiddens),拼接为(seq_len,batch_size,num_hiddens)的三维张量
# 即,将解码器各时间步的输出拼接为序列,并最终映射为词元概率分布序列,从而生成完整的输出句子
# 全连接层变换后,outputs的形状为(num_steps,batch_size,vocab_size)
outputs = self.dense(torch.cat(outputs, dim=0))
return outputs.permute(1, 0, 2), [enc_outputs, hidden_state,
enc_valid_lens]
@property
def attention_weights(self):
''' 注意力权重访问
返回:每个解码时间步的注意力权重(用于可视化对齐关系)
'''
return self._attention_weights下面使用 包含7个时间步的4个序列输入的 小批量测试 Bahdanau注意力解码器:
python
# 创建编码器
# 将长度可变序列 → 固定形状的编码状态
encoder = common.Seq2SeqEncoder(vocab_size=10, # 词表大小 即 输入维度为10
embed_size=8, # 每个单词被表示为8维的向量
num_hiddens=16, # 隐藏层的维度 即 单个隐藏层的神经元数量
num_layers=2) # 隐藏层的堆叠次数
encoder.eval() # 设置为评估模式(关闭dropout等训练专用层)
# 创建带注意力的解码器
# 固定形状的编码状态 → 将长度可变序列
decoder = common.Seq2SeqAttentionDecoder(vocab_size=10, embed_size=8, num_hiddens=16, num_layers=2)
decoder.eval() # 设置为评估模式(关闭dropout等训练专用层)
# 创建输入数据 (batch_size=4, 序列长度=7)
# 总共4个批次数据,每批次数据的长度 即 时间步 为7
X = torch.zeros((4, 7), dtype=torch.long) # (batch_size,num_steps)
# 编码器处理
# 这里编码器出来output形状:(batch_size,num_steps,num_hiddens)(PyTorch的GRU默认输出格式)
# state形状:(num_layers,batch_size,num_hiddens)
enc_outputs = encoder(X) # outputs: (4,7,16), hidden_state: (2,4,16)
# 初始化解码器状态
# 将编码器的输出转换成 解码器所需的状态
state = decoder.init_state(enc_outputs, None) # outputs调整为(7,4,16)
output, state = decoder(X, state) # 前向传播:解码(假设输入X作为初始输入)
# 检查输出维度和状态结构
print(f"投影到词表空间的所有时间步输出形状:{output.shape}") # 预期: torch.Size([4, 7, 10])
print(f"更新后的解码器状态三元组长度:{len(state)}") # 3: [enc_outputs, hidden_state, enc_valid_lens]
print(f"编码器输出: {state[0].shape}") # torch.Size([4, 7, 16])
print(f"解码器隐藏状态的层数:{len(state[1])}")
print(f"首层隐藏状态形状: {state[1][0].shape}") # torch.Size([4, 16])
4.3. 训练
python
# 下载器与数据集配置
# 为 time_machine 数据集注册下载信息,包括文件路径和校验哈希值(用于验证文件完整性)
downloader = common.C_Downloader()
DATA_HUB = downloader.DATA_HUB # 字典,存储数据集名称与下载信息
DATA_URL = downloader.DATA_URL # 基础URL,指向数据集的存储位置
# 注册数据集信息到DATA_HUB全局字典
# 格式:(数据集URL, MD5校验值)
DATA_HUB['fra-eng'] = (DATA_URL + 'fra-eng.zip', # 完整下载URL(DATA_URL是d2l定义的基准URL)
'94646ad1522d915e7b0f9296181140edcf86a4f5') # 文件MD5,用于校验下载完整性与 (现代循环神经网络------动手学深度学习9-CSDN博客中的7. 序列到序列学习(seq2seq)7.4. 训练)类似:
- 在这里指定超参数,
- 实例化一个带有Bahdanau注意力的编码器和解码器,
- 并对这个模型进行机器翻译训练。
由于新增的注意力机制,训练要比没有注意力机制的 9.7.4节慢得多。
python
# 词嵌入维度,隐藏层维度,rnn层数,失活率
embed_size, num_hiddens, num_layers, dropout = 32, 32, 2, 0.1
batch_size, num_steps = 64, 10 # 批量大小,序列最大长度
lr, num_epochs, device = 0.005, 250, common.try_gpu() # 学习率,训练轮数,设备选择
""" 数据预处理
train_iter: 训练数据迭代器(自动进行分词、构建词汇表、填充和批处理)
src_vocab/tgt_vocab: 源语言和目标语言的词汇表对象(包含词元到索引的映射)
"""
train_iter, src_vocab, tgt_vocab = common.load_data_nmt(downloader, batch_size, num_steps)
# 模型构建
"""
编码器结构:
- 嵌入层:将词元索引映射为32维向量
- GRU层:2层堆叠,每层32个隐藏单元,带0.1的dropout
- 输出:所有时间步的隐藏状态(用于注意力计算)和最终隐藏状态(初始化解码器)
"""
encoder = common.Seq2SeqEncoder(
len(src_vocab), embed_size, num_hiddens, num_layers, dropout)
"""
解码器核心创新点:
- 注意力机制:加性注意力(Bahdanau风格),在每个时间步动态生成上下文向量
- 输入拼接:词嵌入(32维)与上下文向量(32维)拼接为64维输入
- GRU层:与编码器维度对齐,保持2层堆叠结构
"""
decoder = common.Seq2SeqAttentionDecoder(
len(tgt_vocab), embed_size, num_hiddens, num_layers, dropout)
net = common.EncoderDecoder(encoder, decoder) # 封装编码器-解码器结构
""" 模型训练
训练过程特点:
- 损失函数:交叉熵损失(忽略填充符)
- 优化器:Adam
- 正则化:梯度裁剪(防梯度爆炸)+ Dropout
- 教师强制(Teacher Forcing):训练时使用真实标签作为输入
"""
common.train_seq2seq(net, train_iter, lr, num_epochs, tgt_vocab, device)
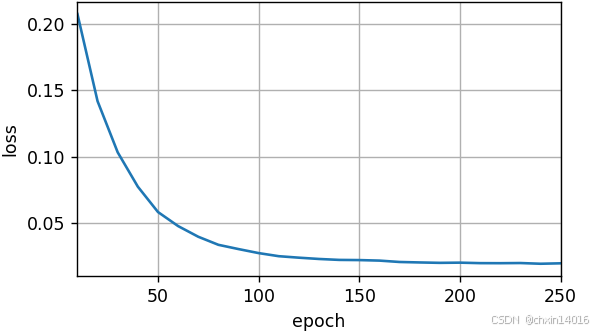
模型训练后,用它将几个英语句子翻译成法语并计算它们的BLEU分数:
- BLEU: (现代循环神经网络------动手学深度学习9-CSDN博客中的 7.6. 预测序列的评估 BLEU(完全相同=1))
python
# 推理与评估
engs = ['go .', "i lost .", 'he\'s calm .', 'i\'m home .']
fras = ['va !', 'j\'ai perdu .', 'il est calme .', 'je suis chez moi .']
for eng, fra in zip(engs, fras):
# 带注意力可视化的预测
translation, dec_attention_weight_seq = common.predict_seq2seq(
net, eng, src_vocab, tgt_vocab, num_steps, device, True)
# BLEU-2评估(双词组匹配精度)
print(f'{eng} => {translation}, ',
f'bleu {common.bleu(translation, fra, k=2):.3f}')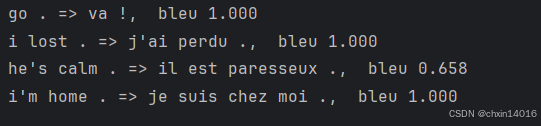
python
# 注意力权重可视化处理
"""
数据处理逻辑:
遍历dec_attention_weight_seq(解码器各时间步的注意力权重序列)
step[0][0][0]即首个batch、首个头、首个查询位置对应的所有键的权重(形状为(key_len,))
1. 提取每个时间步的注意力权重矩阵(batch_size=1, num_heads=1, query_pos, key_pos)
2. .cat(, 0)沿时间维度拼接所有权重矩阵
3. .reshape()调整形状为(1, 1, num_queries, num_keys)
"""
attention_weights = torch.cat([step[0][0][0] for step in dec_attention_weight_seq], 0).reshape((
1, 1, -1, num_steps))训练结束后,下面通过可视化注意力权重 会发现,每个查询都会在键值对上分配不同的权重,这说明 在每个解码步中,输入序列的不同部分被选择性地聚集在注意力池中。
python
""" 绘制注意力热图
可视化说明:
- 横轴:源语言句子位置(编码器时间步)
- 纵轴:目标语言生成位置(解码器时间步)
- 颜色深浅:注意力权重大小(红色越深表示关注度越高)
- 典型对齐模式:对角线(单调对齐)、斜线(跨词对齐)
"""
# 加上一个包含序列结束词元
common.show_heatmaps(
attention_weights[:, :, :, :len(engs[-1].split()) + 1].cpu(),
xlabel='Key positions', ylabel='Query positions')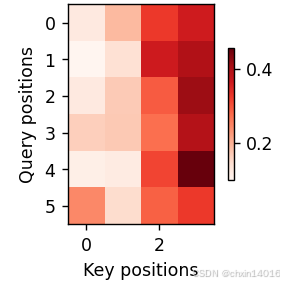
小结
在预测词元时,若非所有输入词元都是相关的,则具有Bahdanau注意力的循环神经网络编码器-解码器会有选择地统计输入序列的不同部分。(通过将上下文变量视为加性注意力池化的输出来实现)
在循环神经网络编码器-解码器中,Bahdanau注意力
将上一时间步的解码器隐状态 视为查询,
在所有时间步的编码器隐状态 同时视为键 和值。
5. 多头注意力
- 线性投影:将Q/K/V从原始维度投影到 num_hiddens维度
- 形状变换(为多头并行计算准备):将张量重塑为多头并行格式
- 处理有效长度(扩展到每个头):若有valid_lens,将其复制到每个注意力头
- 整体丢去 并行计算多头注意力:每个头独立计算缩放点积注意力
- 逆转形状变换(恢复原始维度):将注意力出来的结果 恢复原始形状
- 最终线性变换:线性层W_o整合多头信息。
每个头各自提炼不同的重点,最后整合。
将输入线性投影到多个子空间,在每个子空间中独立计算注意力,最后将结果合并。
不同的头各自提炼不同方面的重点,整合起来得到简洁准确的总结。
- 文本摘要:提取关键信息后缩句
- 图像分类:识别复杂图案中的物体
- 目标检测:找出图像中的多个目标并定位
- 图像-文本匹配:判断图片和文字是否相关
- 视频-文本描述:为视频生成合适的文字说明
设计目的:
- 当给定相同的查询、键和值的集合时,让模型可以基于相同的注意力机制学习到不同行为,
- 然后将不同的行为作为知识组合起来,捕获序列内各种范围的依赖关系 (例如,短 / 长距离依赖关系)。
- 允许注意力机制组合使用查询、键和值的不同 子空间表示(representation subspaces)。
实现方式:
- 用独立学习得到的
组不同的 线性投影(linear projections) 来变换查询、键和值 (而非 只使用单独一个注意力汇聚)。
- 然后,这
组变换后的查询、键和值 并行地送到注意力汇聚中。
- 最后,将这
个注意力汇聚的输出拼接在一起,并通过另一个可学习的线性投影进行变换, 以产生最终输出。
- (对于
个注意力汇聚输出,每一个注意力汇聚都被称作一个头(head) )
这种设计被称为多头注意力 (multihead attention) (Vaswani et al., 2017)。图10.5.1 展示了使用全连接层来实现可学习的线性变换的多头注意力。
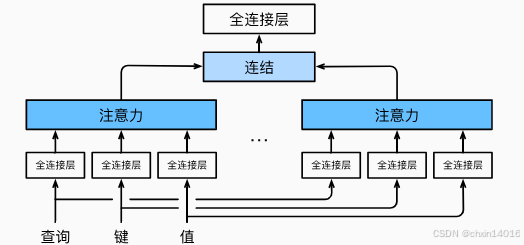 图10.5.1 多头注意力:多个头连结然后线性变换
图10.5.1 多头注意力:多个头连结然后线性变换
5.1. 模型
在实现多头注意力之前,先用数学语言将该模型形式化地描述出来。给定:
- 查询
- 键
- 值
每个注意力头(
)的计算方法为:
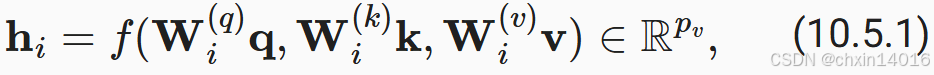
其中,可学习的参数包括 、
和
,以及代表注意力汇聚的函数
。
可以是(3. 注意力评分函数)中的 加性注意力和缩放点积注意力。
多头注意力的输出需要经过另一个线性转换,它对应着 个头连结后的结果,因此其可学习参数是
:
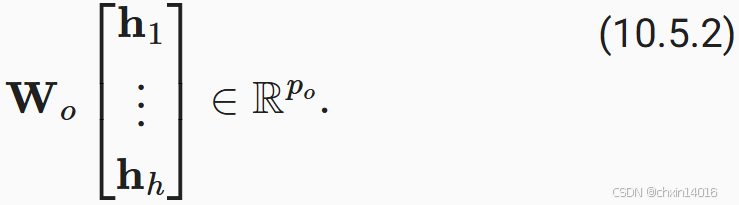
总结下来多头注意力的计算过程就是:(并行计算多个注意力头,捕捉不同类型的依赖关系)
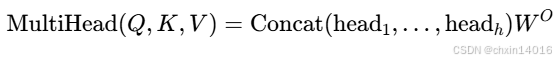
基于该设计,每个头都可能会关注输入的不同部分,可以表示 比简单加权平均值更复杂的函数。
python
import math
import torch
from torch import nn
from common5.2. 实现
在实现过程中通常选择缩放点积注意力作为每一个注意力头。
- 为了避免计算代价和参数代价的大幅增长,设定
。
- 即 查询、键、值的单头维度(每个头处理的向量维度)皆相同,=总输出维度的1/h
- 即 【单头维度=总维度/头数】
:多头注意力最终输出的总维度(所有头拼接后的维度)
- 值得注意的是,若将查询、键和值的线性变换的输出数量设置为
, 则可以并行计算
个头。
- 即 单头维度×头数=总输出维度
- 即 每个头的维度贡献
(或
,
),h个头拼接后总维度为
。
- 在下面的实现中,
通过参数
num_hiddens指定。
python
class MultiHeadAttention(nn.Module):
"""多头注意力"""
def __init__(self, key_size, query_size, value_size, num_hiddens,
num_heads, dropout, bias=False, **kwargs):
super(MultiHeadAttention, self).__init__(**kwargs)
self.num_heads = num_heads # 并行注意力头的数量
self.attention = DotProductAttention(dropout) # 放缩点集注意力模块
# 定义线性投影层(将输入映射到不同子空间)
self.W_q = nn.Linear(query_size, num_hiddens, bias=bias) # Q投影
self.W_k = nn.Linear(key_size, num_hiddens, bias=bias) # K投影
self.W_v = nn.Linear(value_size, num_hiddens, bias=bias) # V投影
self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias) # 输出拼接后的线性变换
def forward(self, queries, keys, values, valid_lens):
"""
queries : 查询向量 (batch_size, 查询数, query_size)
keys : 键向量 (batch_size, 键值对数, key_size)
values : 值向量 (batch_size, 键值对数, value_size)
valid_lens: 有效长度 (batch_size,) 或 (batch_size, 查询的个数)
即 q,k,v形状: (batch_size,查询或者"键-值"对的个数,num_hiddens)
"""
# 1. 线性投影:将Q/K/V从原始维度投影到 num_hiddens维度
# 投影后形状: (batch_size, 查询数/键值对数, num_hiddens)
queries = self.W_q(queries)
keys = self.W_k(keys)
values = self.W_v(values)
# 2. 形状变换(为多头并行计算准备):用transpose_qkv将张量重塑为多头并行格式
# 经过变换后,输出的 q,k,v 的形状:
# (batch_size*num_heads,查询或者"键-值"对的个数,num_hiddens/num_heads)
queries = transpose_qkv(queries, self.num_heads)
keys = transpose_qkv(keys , self.num_heads)
values = transpose_qkv(values , self.num_heads)
# 3. 处理有效长度(扩展到每个头):若有valid_lens,将其复制到每个注意力头
if valid_lens is not None:
# 作用:将有效长度复制num_heads次并保持维度 (batch_size*num_heads, ...)
# 在轴0,将第一项(标量或者矢量)复制num_heads次,
# 然后如此复制第二项,然后诸如此类
valid_lens = torch.repeat_interleave(
valid_lens, repeats=self.num_heads, dim=0)
# 4. 并行计算多头注意力:每个头独立计算缩放点积注意力
# 输出形状:(batch_size*num_heads,查询个数,num_hiddens/num_heads)
output = self.attention(queries, keys, values, valid_lens)
# 5. 逆转形状变换(恢复原始维度):用transpose_output恢复原始形状
# 输出拼接后形状: (batch_size, 查询数, num_hiddens)
# output_concat的形状:(batch_size,查询的个数,num_hiddens)
output_concat = transpose_output(output, self.num_heads)
# 6. 最终线性变换:线性层W_o整合多头信息
return self.W_o(output_concat)为了能够使多个头并行计算, 上面的MultiHeadAttention类将使用下面定义的两个转置函数。
- transpose_qkv :将张量重塑为多头并行计算格式
- transpose_output:将多头输出恢复为原始维度格式
- 具体来说,
transpose_output函数反转了transpose_qkv函数的操作。
python
# 辅助函数:为多头并行计算变换形状
def transpose_qkv(X, num_heads):
"""为了 多注意力头的并行计算 而变换形状
即 将张量重塑为多头并行计算格式
示例:
输入 X:(2, 4, 100)(batch_size=2, seq_len=4, num_hiddens=100)
输出:(2 * 5, 4, 20)(num_heads=5, depth_per_head=20)
"""
# 增加num_heads维度
# 输入X的形状:(batch_size,查询或者"键-值"对的个数,num_hiddens)
# 输出X的形状:(batch_size,查询或者"键-值"对的个数,num_heads,num_hiddens/num_heads)
X = X.reshape(X.shape[0], X.shape[1], num_heads, -1) # 增加num_heads维度
# 输出X的形状:(batch_size,num_heads,查询或者"键-值"对的个数, num_hiddens/num_heads)
X = X.permute(0, 2, 1, 3) # 每批次数据皆按头数分批,几个头就几批
# 最终合并batch和num_heads维度: (batch_size*num_heads, 序列长度, 每个头的维度)
# 最终输出的形状:(batch_size*num_heads,查询或者"键-值"对的个数, num_hiddens/num_heads)
return X.reshape(-1, X.shape[2], X.shape[3])
# 辅助函数:逆转transpose_qkv的形状变换
def transpose_output(X, num_heads):
"""逆转transpose_qkv函数的操作
即 将多头输出恢复为原始维度格式 """
# 输入形状: (batch_size*num_heads, 序列长度, 每个头的维度)
# 恢复维度: (batch_size, num_heads, 序列长度, 每个头的维度)
X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
X = X.permute(0, 2, 1, 3) # (batch_size, seq_len, num_heads, 每个头的维度depth_per_head)
# 合并最后两个维度: (batch_size, 序列长度, num_hiddens)
return X.reshape(X.shape[0], X.shape[1], -1)下面使用键和值相同的小例子来测试编写的MultiHeadAttention类。
- 多头注意力输出的形状是(
batch_size,num_queries,num_hiddens)
python
num_hiddens, num_heads = 100, 5 # 隐藏层维度,注意力头数
attention = common.MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens,
num_hiddens, num_heads, 0.5)
attention.eval() # 设置为评估模式(关闭dropout等训练专用层)
print(f"[多头注意力]模型结构概览:\n{attention}")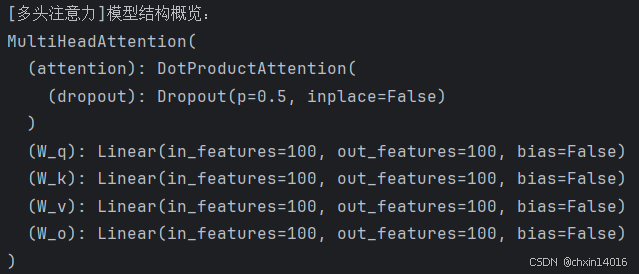

python
batch_size, num_queries = 2, 4 # 批量大小,查询数量
# 键值对数,序列有效长度
# (因为批量大小为2,所以第一个批量的序列长度中有效长度为3,第二个批量的序列长度中有效长度为2)
# 序列长度:对于X来说是查询数4,对于Y来说是键值对数6
num_kvpairs, valid_lens = 6, torch.tensor([3, 2]) # 第二个查询只关注前2个键值对
# 输入数据:全1张量用于测试
# X的形状是(batch_size, num_queries, num_hiddens)
# 即 每个样本有num_queries个查询向量,每个向量维度是num_hiddens
# Y的形状是(batch_size, num_kvpairs, num_hiddens)
# 即 每个样本有num_kvpairs个键值对,每个键和值的维度也是num_hiddens
X = torch.ones((batch_size, num_queries, num_hiddens)) # 查询向量
Y = torch.ones((batch_size, num_kvpairs, num_hiddens)) # 键值对
# 前向传播
output = attention(X, Y, Y, valid_lens)
print(f"输出形状:{output.shape}")
小结
多头注意力融合了来自于多个注意力汇聚的不同知识,这些知识的不同来源于相同的查询、键和值的不同的子空间表示。
基于适当的张量操作,可以实现多头注意力的并行计算。
6. 自注意力和位置编码
在深度学习中,经常使用卷积神经网络(CNN)或循环神经网络(RNN)对序列进行编码。 想象一下,有了注意力机制之后,将词元序列输入注意力池化中,以便同一组词元同时充当查询、键和值。即 每个查询都会关注所有的键-值对并生成一个注意力输出。
自注意力 (self-attention) (Lin et al., 2017, Vaswani et al., 2017)Vaswani et al., 2017:
- 也被称为内部注意力 (intra-attention) (Cheng et al., 2016, Parikh et al., 2016, Paulus et al., 2017)
- 查询、键 和 值 均来自同一组输入序列 (如词元序列)。
- 通过计算序列中每个词元与其他所有词元的关联权重,生成上下文感知的表示。
本节将使用自注意力进行序列编码,以及如何使用序列的顺序作为补充信息。
python
import math
import torch
from torch import nn
from common6.1. 自注意力(qkv皆为同一序列)
- 输入 :一个由词元组成的序列
,其中任意
(
)
- 该序列的自注意力输出 :一个长度相同的序列
,其中:
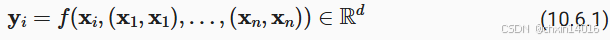
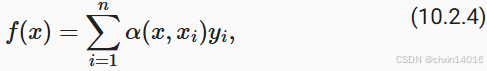 x:查询
x:查询
(x_i, y_i) :键值对
根据 (10.2.4)中定义的注意力汇聚函数。下面的代码片段:
- 是基于多头注意力对一个张量完成自注意力的计算
- 张量的形状为(批量大小,时间步的数目或词元序列的长度,
)
- 输出与输入的张量形状相同
python
num_hiddens, num_heads = 100, 5 # 隐藏层维度,注意力头数
attention = common.MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens,
num_hiddens, num_heads, 0.5)
attention.eval() # 设置为评估模式(关闭dropout等训练专用层)
print(f"模型结构:\n{attention}")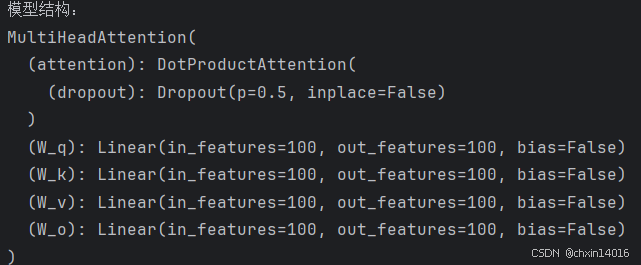
python
# 批量大小,查询数量,序列有效长度(对于X来说,序列长度是键值对数)
batch_size, num_queries, valid_lens = 2, 4, torch.tensor([3, 2])
# 输入数据:全1张量用于测试
# 张量形状(批量大小,时间步的数目或词元序列的长度,d)
# 查询数量,等同于序列长度(时间步数/词元数),表示每个序列包含的词元数量(此处为4)
# d:隐藏层维度(即特征向量长度)
X = torch.ones((batch_size, num_queries, num_hiddens))
output = attention(X, X, X, valid_lens)
print(f"输出形状:{output.shape}")
6.2. 比较卷积神经网络、循环神经网络和自注意力
接下来比较下面几个架构,
- 目标:都是将由n个词元组成的序列映射到另一个长度相等的序列,
- 其中的每个输入词元或输出词元都由d维向量表示。
具体来说,将比较的是
- 卷积神经网络、
- 循环神经网络 和
- 自注意力
这几个架构的
- 计算复杂性、
- 顺序操作 和
- 最大路径长度。
注意:顺序操作会妨碍并行计算,而
- 任意的序列位置组合之间的路径越短,
- 则越能轻松学习序列中的远距离依赖关系 (Hochreiter et al., 2001)。
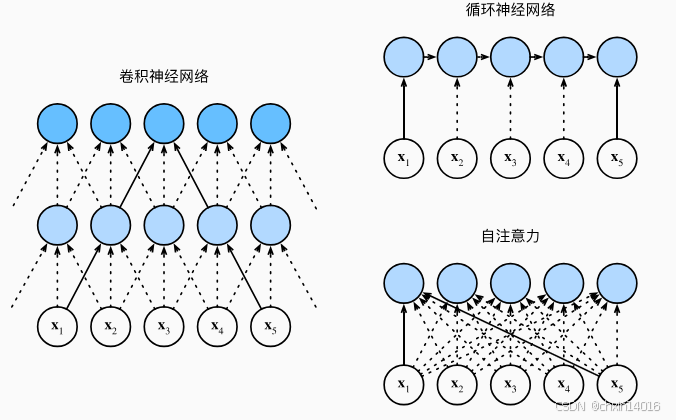 图10.6.1 比较
图10.6.1 比较
卷积神经网络(填充词元被忽略)、
循环神经网络 和
自注意力
三种架构
考虑一个卷积核大小为k的卷积层。 后面章节会提供关于使用卷积神经网络处理序列的更多详细信息。 目前只需知道,由于序列长度是n,输入和输出的通道数量都是d,所以卷积层的计算复杂度为 。如 图10.6.1所示,卷积神经网络是分层的,因此为有
个顺序操作, 最大路径长度为
。例如,
和
处于 图10.6.1中卷积核大小为3的双层卷积神经网络的感受野内。
当更新循环神经网络的隐状态时, 权重矩阵和 d维隐状态的乘法计算复杂度为
。 由于序列长度为 n,因此循环神经网络层的计算复杂度为
。根据 图10.6.1,有
个顺序操作无法并行化,最大路径长度也是
。
在自注意力中,查询、键和值都是 矩阵。 考虑 (10.3.5)中缩放的"点-积"注意力,其中
矩阵 乘以
矩阵。 之后输出的
矩阵 乘以
矩阵。因此,自注意力具有
计算复杂性。正如在 图10.6.1中所讲,每个词元都通过自注意力直接连接到任何其他词元。 因此,有
个顺序操作可以并行计算,最大路径长度也是
。
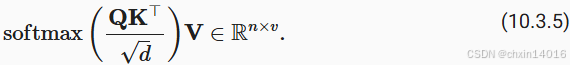
:查询矩阵(Query),形状为
(..., seq_len_q, d_k):键矩阵(Key),形状为
(..., seq_len_k, d_k):值矩阵(Value),形状为
(..., seq_len_v, d_v):键和查询的维度(dimension of key)
:缩放因子(Scaling Factor),这是其与原始点积注意力的唯一区别。
总而言之,
- 卷积神经网络 和自注意力 都拥有并行计算 的优势,而且自注意力 的最大路径长度最短。
- 但因自注意力计算复杂度是关于序列长度的二次方,所以在很长的序列中计算会非常慢。
列表总结 架构对比:卷积神经网络(CNN) vs 循环神经网络(RNN) vs 自注意力
| 维度 | 卷积神经网络(CNN) | 循环神经网络(RNN) | 自注意力(Self-Attention) |
|---|---|---|---|
| 计算复杂度 | |||
| 顺序操作 | 分层结构, 顺序操作数为 |
完全顺序依赖, 顺序操作数为 |
完全并行, 顺序操作数为 |
| 最大路径长度 | |||
| 关键特性 | 局部感受野(通过堆叠层扩大) ,适合局部模式 | 长期依赖难捕获 (梯度消失/爆炸问题) | 全局依赖捕获能力强, 但长序列计算慢 |
图示解读:
- CNN通过卷积核分层处理,需多层才能覆盖长距离依赖(如核大小3的双层CNN最大路径长度为5);
- RNN需按时间步顺序处理,隐状态逐个更新,路径长度与序列长度线性相关;
- 自注意力通过查询-键-值机制,每个词元直接与所有词元交互,路径长度恒为1。
6.3. 位置编码(Transformer的位置编码)
- 在处理词元序列时,循环神经网络是逐个的重复地处理词元的,而自注意力则因为并行计算而放弃了顺序操作。
- 为了使用序列的顺序信息,通过在输入表示中添加 位置编码 (positional encoding) 来注入绝对的或相对的位置信息 (即 需显式编码位置)。
- 位置编码可通过学习得到,也可直接固定得到。
固定位置编码 :基于正弦 / 余弦函数 (Vaswani et al., 2017)。
假设
- 输入:
包含一个序列中n个词元的d维嵌入表示
- 位置编码:形状与输入相同的 位置嵌入矩阵
- 输出:
,
- 矩阵第
行、第
列 和
列上的元素为:
- 矩阵第
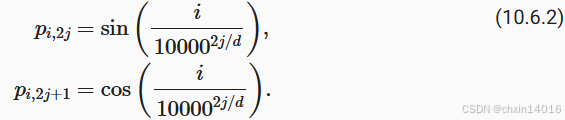
- 行 i :词元在序列中的位置
- 列 j :位置编码的不同维度
- d:嵌入维度
关键点解析
-
为什么用
sin/cos交替?通过正弦余弦的周期性变化,在有限维度中编码无限位置信息,同时允许模型学习相对位置。
- 连续性优势 :与二进制离散翻转不同,三角函数提供平滑的连续变化,且浮点数表示比二进制更节省空间(无需存储整数字符串)。
-
为什么除以
10000^{2j/d}?指数衰减使低维度(对应
j较小)捕获高频信号(短周期),高维度捕获低频信号(长周期),形成多尺度编码。-
频率衰减 :分母中的指数项 10000^{2j/d} 使得维度索引 j 越大(即特征维度越高),频率越低
-
j=0(最低维) :频率
(每个位置变化)
-
j=10(较高维):频率
(可能每100个位置变化一次)
-
-
归一化必要性
将
2j/d归一化到[0,1)保证指数计算稳定性,避免数值过大或过小。 -
通过这种设计:
- 位置编码能够为每个位置生成唯一 的、具有周期性变化的向量表示,
- 使模型能够区分不同位置并捕捉相对位置关系。
乍一看,这种基于三角函数的设计看起来很奇怪。在解释该设计之前,先在下面的PositionalEncoding类中实现它:
python
class PositionalEncoding(nn.Module):
"""位置编码模块:为序列注入绝对位置信息
构造函数中 实现了位置编码的预计算
在训练/推理时只需根据实际序列长度动态截取,既节省内存又提高效率
max_len :词元在序列中的位置 总数
num_hiddens :位置编码的不同维度 总数即总维度
实例化类对象传入时,num_hiddens作为嵌入维度
"""
# num_hiddens 嵌入维度
def __init__(self, num_hiddens, dropout, max_len=1000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(dropout)
# 创建一个足够长的P(位置嵌入矩阵)
# 预计算位置编码矩阵(1, max_len, num_hiddens)
self.P = torch.zeros((1, max_len, num_hiddens)) # 初始化三维张量
# 生成位置编码的频率分量(基于论文公式)
# 公式:
# PE(pos,2j) = sin(pos/(10000^{2j/d}))
# PE(pos,2j+1) = cos(...)
# positions为列向量,表示行i的 位置索引 [0,1,...,max_len-1]
# dims:分母中10000的幂,
# arange(0,n,2)从0到n-1,步长为2,生成【偶数】索引序列[0,2,4,...,n-1],对应公式中的2j
# /num_hiddens 归一化到[0,1)区间(例如num_hiddens=512时,dims=[0/512, 2/512, ..., 510/512])
positions = torch.arange(max_len).float().reshape(-1, 1) # 形状(max_len,1)
dims = torch.arange(0, num_hiddens, 2).float() / num_hiddens # 维度索引归一化,形状(num_hiddens/2,)
freqs = torch.pow(10000, dims) # 10000^(2j/d) 计算频率分母项,形状同dims
# sin/cos的输入值(pos / (10000^{2j/d}))
# 广播除法:将positions的每一行除以freqs的所有元素
# 出来X形状(词元在序列中的位置总数max_len,位置编码的总维度num_hiddens/2),/2是因为前面步进为2
# 例如 pos=2, j=0时:X[2][0] = 2 / 10000⁰ = 2
X = positions / freqs # 即(行i/(10000^{2j/d})),j是列
# 填充位置编码矩阵:偶数维度用sin,奇数维度用cos
# 0::2 从0开始步进为2的切片,即 偶数列 0,2,4,8,...
# 1::2 从1开始步进为2的切片,即 奇数列 1,3,5,7,...
self.P[:, :, 0::2] = torch.sin(X) # 所有偶数列填充sin值
self.P[:, :, 1::2] = torch.cos(X) # 所有奇数列填充cos值
# 构造函数里 X=positions/freqs 的 X 在用于生成self.P后即被销毁
# 前向传播里 X.shape[1] 用的 X 是来自于函数头的参数X,即 实际输入的数据
def forward(self, X):
"""前向传播:将位置编码加到输入上
前向传播中的截取操作 pos_embed=self.P[:, :seq_len,:]:动态适配输入序列长度
核心目的:避免固定max_len导致的内存浪费,实现按需截取。
"""
# 根据实际序列长度截取位置编码(避免固定max_len导致内存浪费)
seq_len = X.shape[1] # X.shape[1] 获取输入序列的实际长度
pos_embed = self.P[:, :seq_len, :].to(X.device) # 按实际序列长度截取位置编码,移动设备兼容性处理
X = X + pos_embed # 绝对位置编码:直接相加,将位置编码加到输入上(广播机制自动对齐batch维度)
return self.dropout(X) # 应用随机失活在位置嵌入矩阵 中,
- 行 代表 词元在序列中的位置,
- 列 代表 位置编码的不同维度。
python
encoding_dim, num_steps = 32, 60 # 嵌入维度,序列步长
pos_encoding = common.PositionalEncoding(encoding_dim, 0) # 创建位置编码器
pos_encoding.eval() # 设置为评估模式(关闭dropout等训练专用层)
# 生成全零输入(模拟嵌入向量)
# ①torch.zeros((1, num_steps, encoding_dim)) 和
# ②torch.zeros(1, num_steps, encoding_dim) 完全等效,无功能差异
# ①是 元组形式 ,符合函数参数传递的通用规范
# ②是 直接参数形式,直接传递多个整数参数,PyTorch内部会自动将其转换为形状元组
X = pos_encoding(torch.zeros((1, num_steps, encoding_dim)))
# 外部再次提取操作:服务于后续处理需求
P = pos_encoding.P[:, :X.shape[1], :] # 提取实际使用的位置编码
''' 可视化特定维度的位置编码变化
P[0, :, 6:10]取第一个批次(batch维度索引0),该批次中的所有词元(序列维度全部保留,从0到seq_len-1)
取每个词元的特征维度中索引6到9的4个维度(对应隐藏层维度索引6,7,8,9)
加转置的原因:调整数据的维度,使能正确将每个特征维度作为单独的曲线绘制,而非将每个位置作为曲线
若原始数据是:
位置0: [v6, v7, v8, v9]
位置1: [v6, v7, v8, v9]
转置后变成:
特征6: [位置0的值, 位置1的值, ...]
特征7: [位置0的值, 位置1的值, ...]
这样,每条曲线就是某个特征维度随位置的变化,符合常见的可视化需求
legend=["Col %d" % d for d in torch.arange(6, 10)] 等价于
legend=[f"Col {d}" for d in range(6, 10)]
'''
common.plot(torch.arange(num_steps), # x轴:0~59的位置索引
P[0, :, 6:10].T, # 选取维度6~9的4个特征
xlabel='Row (position)', # x轴标签
figsize=(6, 2.5), # 图像尺寸
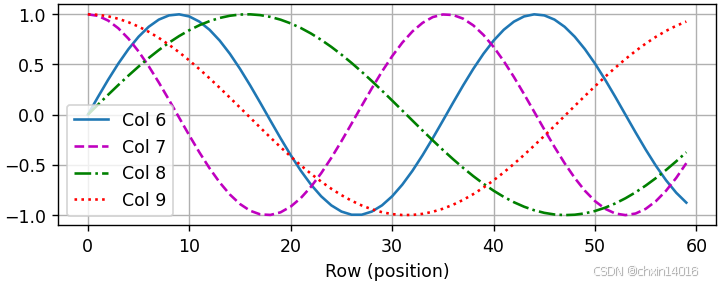
legend=["Col %d" % d for d in torch.arange(6, 10)]) # 图例从上面的例子中可看到(如下图所示):
- 位置嵌入矩阵的 第6列和第7列的频率 高于第8列和第9列。
- 第6列和第7列之间的偏移量(第8列和第9列相同)是由于正弦函数和余弦函数的交替。
6.3.1. 绝对位置信息
核心观点:
- 二进制中高位比特变化频率低,低位比特变化频率高;
- 位置编码 通过三角函数设计 实现类似但连续的频率衰减。
二进制表示的频率特性
以4位二进制数表示位置(如0000到1111共16个位置):
- 最高位(第3位):每8个位置翻转一次(频率=1/8)
- 次高位(第2位):每4个位置翻转一次(频率=1/4)
- 次低位(第1位):每2个位置翻转一次(频率=1/2)
- 最低位(第0位) :每1个位置翻转一次(频率=1/1)
直观理解:高位比特控制粗粒度位置变化,低位比特控制细粒度位置变化。 - (沿着编码维度单调降低的频率与绝对位置信息的关系)
下面打印出 的二进制表示形式,以便演示以上观点:
python
# 打印0到7的二进制表示形式,演示观点:随着编码维度增加,比特值的交替频率正在单调降低
for i in range(8):
print(f'{i}的二进制是:{i:>03b}') # 格式化输出二进制(3位宽度右对齐)
在二进制表示中,较高比特位的交替频率低于较低比特位,与下面的热图所示相似,
- 但位置编码通过使用三角函数在编码维度上降低频率。即
- 三角函数提供平滑的连续变化
- 频率衰减 :分母中的指数项 10000^{2j/d} 使得维度索引 j 越大(即特征维度越高),频率越低
- 由于输出是浮点数,因此此类连续表示比二进制表示法更节省空间。即
- 浮点数表示比二进制更节省空间(无需存储整数字符串)
python
# 热图可视化:展示位置编码矩阵的全局模式
# 取出第一个批次(batch维度索引0)的所有词元的和所有特征维度,在第0维的位置插入两个长度为1的维度
# 插入的两个长度为1的维度是指子图行数和列数,
# 多个子图指的是将多个不同的热图子图显示在同一个画框(即一个图形窗口)内,而这里只有一个子图热图
P = P[0, :, :].unsqueeze(0).unsqueeze(0) # 调整维度为(1,1,seq_len,dim)
common.show_heatmaps(P,
xlabel='Column (encoding dimension)', # x轴:编码维度
ylabel='Row (position)', # y轴:序列位置
figsize=(3.5, 4),
cmap='Blues') # 蓝色系配色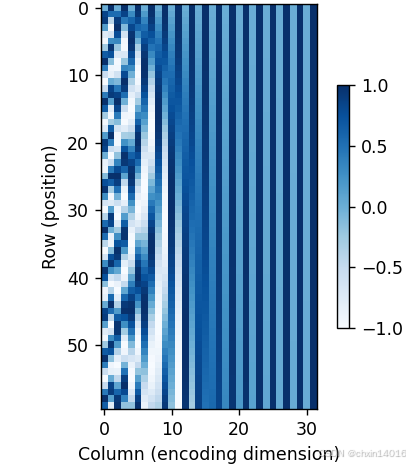
6.3.2. 相对位置信息
除了捕获绝对位置信息之外,上述的位置编码还允许模型学习得到 输入序列中相对位置信息。
- 核心观点 :位置编码通过三角函数的线性性质,使得任意位置对的相对距离可被模型隐式学习。
这是因为对于任何确定的位置偏移 (固定偏移量),位置
处 的位置编码可以线性投影位置
处的位置编码来表示。
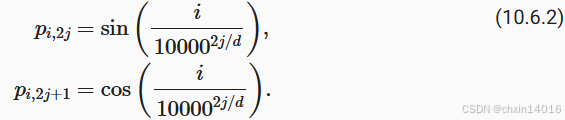
这种投影的数学解释是,令 (第 i 维的角频率),对于任何确定的位置偏移
, (10.6.2)中的任何一对
都可以线性投影到
:
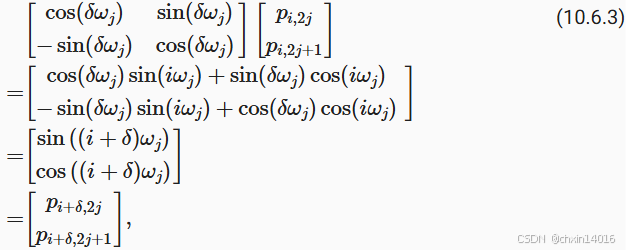
2×2投影矩阵不依赖于任何位置的索引 。
核心观点 :位置编码通过三角函数的线性性质,使得任意位置对的相对距离可被模型隐式学习。
:第 i 维的角频率
- 即
,其中
:仅依赖于 k 的旋转矩阵
小结
自注意力:查询、键和值皆来自同一组输入。
卷积神经网络、自注意力:皆拥有并行计算的优势,且自注意力的最大路径长度最短。但是:
因自注意力计算复杂度是关于序列长度的二次方,
所以在很长的序列中计算会非常慢。
为了使用序列的顺序信息,可以通过在输入表示中添加位置编码,来注入绝对的或相对的位置信息。
7. Transformer
(6.2. 比较卷积神经网络、循环神经网络和自注意力)中比较了卷积神经网络(CNN)、循环神经网络(RNN)和自注意力(self-attention)。
- 自注意力 同时具有并行计算 和最短的最大路径长度这两个优势。
- 因此,使用自注意力来设计深度架构是很有吸引力的。
- 对比之前仍然依赖循环神经网络实现输入表示的自注意力模型 (Cheng et al., 2016, Lin et al., 2017, Paulus et al., 2017),
- Transformer模型完全基于注意力机制,没有任何卷积层或循环神经网络层 (Vaswani et al., 2017)。
- 尽管Transformer最初是应用于在文本数据上的序列到序列学习,但现在已经推广到各种现代的深度学习中,例如语言、视觉、语音和强化学习领域。
Transformer的核心优势
- 并行计算能力 :
自注意力机制(Self-Attention)无需像RNN那样按序列逐步处理输入,可同时计算所有位置的依赖关系,显著提升训练效率。- 最短路径长度 :
自注意力能直接建模任意位置间的关系,路径长度为1(RNN需O(n)步,CNN需O(log n)层),缓解长序列依赖问题。- 纯注意力架构 :
完全摒弃CNN和RNN,仅依赖自注意力、前馈网络和位置编码,实现更灵活的全局依赖建模。
7.1. 模型
 图10.4.1 一个带有Bahdanau注意力的 循环神经网络编码器-解码器模型
图10.4.1 一个带有Bahdanau注意力的 循环神经网络编码器-解码器模型
编码器与所有隐藏状态加权和,得到 每个时间步单独的上下文变量
权重由当前解码器状态与所有编码器状态的相关性决定
Transformer作为编码器-解码器架构的一个实例,其整体架构图在 图10.7.1中展示。正如所见到的:
- Transformer:由编码器和解码器组成。(编码器-解码器结构)
- 与 图10.4.1中基于Bahdanau注意力实现的序列到序列的学习相比:
- 基于Bahdanau注意力实现的序列到序列的学习:叠加加性注意力模块 和 rnn层。
- Transformer的编码器和解码器:基于自注意力的模块叠加而成,
- 源(输入)序列 和 目标(输出)序列的嵌入 (embedding)表示将加上位置编码(positional encoding),再分别输入到编码器和解码器中。
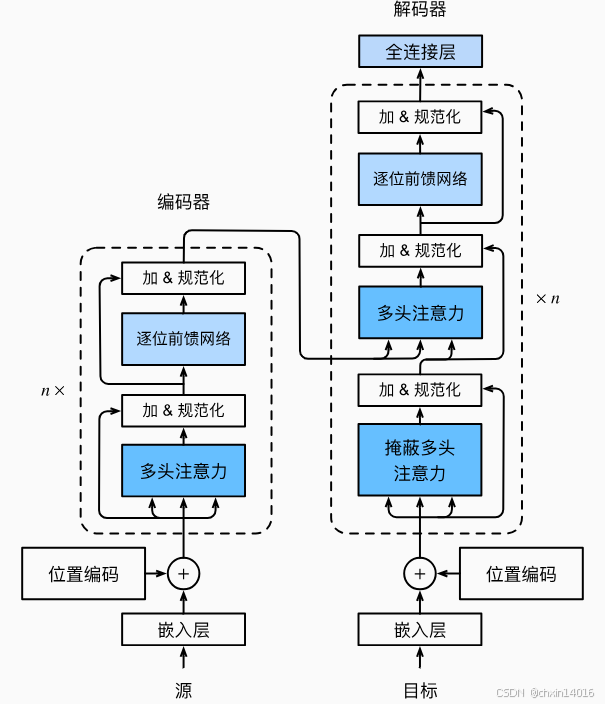 图10.7.1 transformer架构
图10.7.1 transformer架构
左侧编码器 :处理输入序列(如源语言句子)
右侧解码器:生成输出序列(如目标语言翻译)
图 图10.7.1中概述了Transformer的架构。
从宏观角度来看,(如图所示,从下到上依次)
- Transformer的编码器(Encoder):
- 输入处理层:
- 嵌入层:将词元转换为向量表示
- 位置编码:添加位置信息(弥补自注意力缺乏位置感知的缺陷)
- N个编码器层(重复堆叠) :每层皆有两个子层(子层表示为
)
- 子层 1:多头自注意力 (multi-head self-attention)汇聚;
- 作用:计算输入序列内部的关系
- 输入查询(Q)、键(K)、值(V)均来自前一个编码器层的输出
- 通过多头机制并行捕捉不同子空间的注意力模式
- 子层 2:基于位置的前馈网络 (positionwise feed-forward network,位置前馈网络Positionwise FFN)
- 作用:对输入序列中每个位置的向量独立进行非线性变换,从而增强模型的表达能力。
- 位置独立处理:FFN 对输入序列的 每个位置向量(如每个词元的d维向量)独立应用相同的全连接层(通常含ReLU激活),不涉及不同位置间的交互。
- 结构 :通常为 两个线性变换层+一个非线性激活函数,公式为:
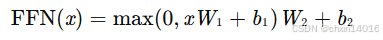 (详情看7.2. 基于位置的前馈网络)
(详情看7.2. 基于位置的前馈网络)
- 子层 1:多头自注意力 (multi-head self-attention)汇聚;
- 加法和层归一化 :残差连接+层归一化 ,稳定训练
- 受 (现代卷积神经网络------动手学深度学习7_动手学深度学习7.1节cpu得跑多久-CSDN博客 6. 残差网络(ResNet))中残差网络的启发,
- 每个子层都采用了残差连接(residual connection)
- 在Transformer中,对于序列中任何位置的任何输入
,都要求满足
,以便残差连接满足
。
- 在残差连接的加法计算之后,紧接着应用层规范化 (layer normalization) (Ba et al., 2016)。
- 因此,输入序列对应的每个位置,Transformer编码器都将输出一个d维表示向量。
- 即 每个子层后添加残差连接(输出=子层输出+输入)和层归一化(Layer Norm),稳定训练过程。
- 输出:为输入序列的每个位置生成d维表示向量
- 输入处理层:
- Transformer解码器(Decoder):
- 解码器结构与编码器类似:也是由N个相同的层叠加而成,且层中使用了残差连接和层规范化。
- 但包含关键差异 :每层包含三个子层(额外组件有两个 )
- 即 除编码器中描述的两个子层外,解码器还在这两子层之间插入了第三个子层,称为编码器-解码器注意力(encoder-decoder attention)层。
- 掩蔽多头自注意力(Masked Multi-Head Self-Attention) :(额外组件 )
- 作用:防止解码时"偷看"未来信息(因果掩码)
- 查询、键、值:皆来自前一解码层的输出
- 但是,通过掩蔽(Mask)确保每个位置仅关注左侧已生成词元(即 确保预测仅依赖于已生成的输出词元),维持自回归(auto-regressive)特性。
- 编码器-解码器注意力(Encoder-Decoder Attention) :(额外组件 )
- 作用:连接编码器输出,实现源序列与目标序列的交互(跨序列关注)
- 查询:来自前一解码器层的输出
- 键和值:来自编码器最终输出 (即 来自整个编码器的输出)
- 位置前馈网络:与编码器相同
- 残差连接与层归一化:同样应用于每个子层后
- 输出:生成目标序列的预测词元
关键技术细节:
- 残差连接与层归一化 :
- 残差连接:缓解梯度消失,允许构建深层网络(如N=6或12)。
- 层归一化:对每个样本的特征维度归一化,稳定训练动态。
训练与推理特点
- 训练阶段 :
- 编码器并行处理整个输入序列,解码器通过掩蔽自注意力逐步生成目标序列(教师强制模式)。
- 推理阶段 :
- 解码器自回归生成词元,每次仅依赖已生成的输出(自回归解码)。
在此之前已经描述并实现了基于缩放点积多头注意力 10.5节和位置编码 10.6.3节。接下来将实现Transformer模型的剩余部分。
python
import math
import pandas as pd
import torch
from torch import nn
from common与传统模型的对比
| 特性 | Transformer | RNN/CNN |
|---|---|---|
| 并行性 | 高(全序列并行计算) | 低(RNN需顺序处理) |
| 长序列依赖 | 优(直接建模任意位置关系) | 差(RNN梯度消失,CNN局部感受野) |
| 计算复杂度 | O(n²)(序列长度n) | RNN: O(n), CNN: O(k·n)(k为卷积核大小) |
| 结构灵活性 | 高(纯注意力,无归纳偏置) | 较低(CNN局部性,RNN时序性) |
实现步骤(处理流程)
- 输入嵌入+位置编码:将词元映射为d维向量并添加位置信息。
- 编码器堆叠:多头自注意力 → 残差+层归一化 → 位置前馈网络 → 残差+层归一化。
- 解码器堆叠 :掩蔽自注意力 → 残差+层归一化 → 编码器-解码器注意力 → 残差+层归一化 → 位置前馈网络 → 残差+层归一化。
- 输出层:线性变换+Softmax生成词元概率分布。
大致总结
Transformer通过自注意力机制:
- 实现了并行化与全局依赖建模的平衡,
- 其编码器-解码器架构配合残差连接和层归一化,支持深层网络训练。
- 该设计不仅革新了NLP领域,还推动了多模态深度学习的发展,成为现代深度学习的基石架构之一。
7.2. 基于位置的前馈网络
逻辑顺序:对输入x进行:全连接层→激活→全连接层。
位置前馈网络 (Positionwise Feed-Forward Network,简称FFN)
- 是Transformer模型中编码器和解码器每个子层的核心组件之一
- 作用 :对输入序列中每个位置的向量独立进行非线性变换,从而增强模型的表达能力。
【核心定义】
- 位置独立处理:FFN 对输入序列的 每个位置向量(如每个词元的d维向量)独立应用相同的全连接层(通常含ReLU激活),不涉及不同位置间的交互。
- 结构 :2个线性变换层 + 1个非线性激活函数组成,公式为:
【设计目的】
- 非线性变换:通过激活函数引入非线性,使模型能够学习复杂的模式。
- 维度扩展与压缩 :
- 第一层线性变换将输入维度从 d 扩展到
(如512→2048),增强特征表达能力。
- 第二层线性变换将维度压缩回 d ,保持输出与输入维度一致,便于后续层处理。
- 位置级特征增强:对每个位置的向量进行独立强化,补充自注意力机制可能忽略的局部模式。
【与自注意力的协作流程】
- 自注意力生成包含全局信息的上下文向量。
- FFN对上下文向量进行非线性变换,提取更高阶特征。
【参数共享与效率】
- 参数共享 :同一层的FFN对所有位置共享相同的 权重矩阵
,
和 偏置
,
,显著减少参数量。
- 计算效率:由于位置独立处理,FFN可并行计算所有位置的变换,与自注意力的并行性一致。
【实际效果】
- 增强模型容量:FFN的深层非线性变换使Transformer能够拟合更复杂的函数。
- 稳定训练:通过维度扩展(如d→dff)和激活函数,缓解梯度消失问题。
- 实证有效性:在原始Transformer论文中,移除FFN会导致性能显著下降,证明其必要性。
【变体与改进】
- 激活函数替换:使用GELU(Gaussian Error Linear Unit)替代ReLU,缓解神经元死亡问题。
- 深度扩展:堆叠多个FFN层(如2层),但需谨慎控制参数量。
- 轻量化设计:在移动端模型中,可减小dff以降低计算成本。
- 基于位置的前馈网络 对序列中的所有位置的表示 进行变换时,使用的是同一个多层感知机(MLP),这就是称前馈网络是基于位置的(positionwise)的原因。
- 在下面的实现中,
- 输入
X:形状(批量大小,时间步数或序列长度,隐单元数或特征维度) - 输出 :形状(批量大小,时间步数或序列长度,
ffn_num_outputs) - 形状转换依据:一个两层的感知机
- 输入
python
# 定义位置前馈网络类(Position-wise Feed-Forward Network)
class PositionWiseFFN(nn.Module):
"""基于位置的前馈网络
特点:对输入序列中每个位置的向量独立进行非线性变换,不涉及位置间交互
结构:两层全连接层 + ReLU激活函数
"""
def __init__(self, ffn_num_input, ffn_num_hiddens, ffn_num_outputs,
**kwargs):
"""
参数说明:
ffn_num_input : 输入特征维度(如词向量维度)
ffn_num_hiddens: 中间层隐藏单元数(通常远大于输入维度)
ffn_num_outputs: 输出特征维度
"""
super(PositionWiseFFN, self).__init__(**kwargs)
# 第一层全连接:维度扩展(输入维度 → 隐藏维度)
self.dense1 = nn.Linear(ffn_num_input, ffn_num_hiddens)
# 非线性激活函数(引入非线性能力)
self.relu = nn.ReLU()
# 第二层全连接:维度压缩(隐藏维度 → 输出维度)
self.dense2 = nn.Linear(ffn_num_hiddens, ffn_num_outputs)
def forward(self, X):
""" 前向传播逻辑:
1. 对输入张量X的每个位置独立应用相同变换
2. 维度变化: (batch_size, seq_length, ffn_num_input)
→ (batch_size, seq_length, ffn_num_hiddens)
→ (batch_size, seq_length, ffn_num_outputs)
"""
# 执行:线性变换 → 激活函数 → 线性变换
return self.dense2(self.relu(self.dense1(X)))下面的例子显示:
- 改变张量的 最里层维度的尺寸,会改变成基于位置的前馈网络 的输出尺寸。
- 因为用同一个多层感知机 对所有位置上的输入进行变换,
- 所以当所有这些位置的输入相同时,其输出也会相同。
python
# 创建FFN实例:输入维度4,隐藏层8,输出维度8(实际常用隐藏层维度远大于输入/输出)
# 注:此处隐藏层维度设为4仅为示例,实际常设为2048等大值
ffn = common.PositionWiseFFN(4, 4, 8)
ffn.eval() # 设置为评估模式(关闭dropout等训练专用层)
# 创建输入数据:2个样本,每个样本3个位置,每个位置4维特征
input_tensor = torch.ones((2, 3, 4)) # 全1张量用于测试
output = ffn(input_tensor) # 执行前向传播
first_sample_output = output[0] # 获取第一个样本的所有位置输出(形状:3个位置 × 8维输出)
print("输入形状:", input_tensor.shape) # torch.Size([2, 3, 4])
print("输出形状:", output.shape) # torch.Size([2, 3, 8])
print("首样本输出:\n", first_sample_output)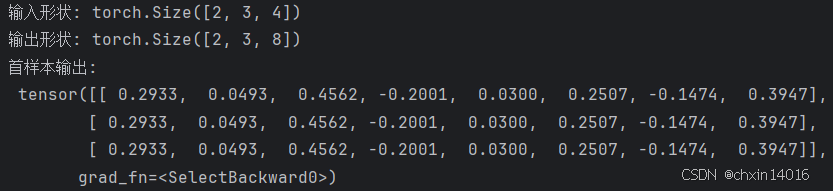
7.3. 残差连接和层规范化
标准顺序:
- 残差输入x经过随机失活后,与子层输出y相加,相加后再经过层归一化(样本内所有特征经过归一化,即每个学生的所有科目成绩归一化)。
- 即 Dropout → 残差连接 → 层归一化
作用:
- 残差连接:缓解梯度消失,支持深层网络训练
- 层归一化:稳定各层输入分布,加速收敛
- Dropout在残差连接前应用:防止子层过拟合同时保护残差梯度通路
 图10.7.1 transformer架构
图10.7.1 transformer架构
左侧编码器 :处理输入序列(如源语言句子)
右侧解码器:生成输出序列(如目标语言翻译)
图10.7.1中的加法和规范化(add&norm)组件:
- 残差连接 + 紧随其后的层规范化(两者都是构建有效的深度架构的关键)
(现代卷积神经网络------动手学深度学习7_动手学深度学习7.1节cpu得跑多久-CSDN博客 5. 批量规范化 (批量归一化))中解释了:在一个小批量的样本内,基于批量规范化对数据进行 重新中心化和重新缩放的调整。
- 层规范化 和 批量规范化 的目标相同,
- 但 层规范化 是基于特征维度进行规范化。
- 批量规范化在计算机视觉中被广泛应用,
- 但在自然语言处理任务中(输入通常是变长序列),层规范化的效果通常>批量规范化。
假设:
- 左列 为 学生样本
- 上行 为 科目分数特征
【层规范化】
- 对每个样本的 所有特征归一化
- 针对批次中的每一个独立的样本,计算该样本所有特征值的均值和方差,并用这个统计量来归一化该样本自身的所有特征。
- 同一学生里,所有科目成绩归一化,看偏科。
- 目的:
- 消除单个样本内部不同特征之间的量纲差异,
- 将每个样本的特征分布统一到稳定的状态,
- 从而更有效地学习样本内的模式关系。
【批量规范化】
- 对每个特征 跨样本归一化
- 计算一个批次(Batch)内所有样本在同一个特征维度上的均值和方差,并用这个统计量来归一化每个样本的该特征值。
- 同一科目中,所有学生的分数归一化,看谁厉害。
- 目的:
- 消除不同特征维度之间的量纲差异,
- 使每个特征维度上的数据分布变得稳定(均值为0,方差为1),
- 从而加速模型训练并提高稳定性。
以下代码对比 不同维度的【层规范化】和【批量规范化】的效果:
python
ln = nn.LayerNorm(2) # 创建【层】归一化对象(对每个样本的所有特征归一化)
bn = nn.BatchNorm1d(2) # 创建【批】归一化对象(对每个特征跨样本归一化)
# 创建输入数据:2个样本,每个样本2个特征
X = torch.tensor([[1, 2], [2, 3]], dtype=torch.float32)
print("在训练模式下计算X的均值和方差:\n")
# 层归一化计算(每个样本独立归一化)
print('layer norm:', ln(X)) # 每个样本的均值和方差独立计算
# 批归一化计算(跨样本归一化)
print('batch norm:', bn(X)) # 所有样本的同一特征共享均值和方差
下面使用残差连接和层规范化来实现AddNorm类:
- 暂退法也被作为正则化方法使用。
python
# 残差连接 + 层归一化模块
class AddNorm(nn.Module):
"""残差连接后进行层规范化
实现残差连接(Residual Connection)后进行层归一化(Layer Normalization)
结构:Sublayer Output → Dropout → (X + Dropout(Y)) → LayerNorm
作用:
1. 残差连接:缓解梯度消失,支持深层网络训练
2. 层归一化:稳定各层输入分布,加速收敛
3. Dropout在残差连接前应用:防止子层过拟合同时保护残差梯度通路
"""
def __init__(self, normalized_shape, dropout, **kwargs):
"""
normalized_shape: 输入张量的最后维度(如[3,4]表示最后维度为4)
dropout: 随机失活概率
"""
super(AddNorm, self).__init__(**kwargs)
self.dropout = nn.Dropout(dropout) # 作用在子层输出
# 层归一化层,作用于残差连接结果(对每个样本的所有特征进行归一化)
self.ln = nn.LayerNorm(normalized_shape)
def forward(self, X, Y):
""" 前向传播
X: 残差输入(通常来自上一层或跳跃连接)
Y: 子层输出(如注意力层/前馈网络输出)
返回:层归一化后的张量
逻辑:
1. 子层输出Y经过Dropout(防止过拟合)
2. 执行残差连接:X + Dropout(Y)
3. 层归一化:稳定数值分布,加速收敛
Dropout(Y) 即为 sublayer
Dropout应作用于:子层输出(Y)之后、残差连接之前
顺序: Dropout → 残差连接 → 层归一化
"""
# 残差连接:输入X与子层输出sublayer相加
# 注意:X和sublayer必须形状相同(如[batch_size, seq_length, dim])
return self.ln(self.dropout(Y) + X)残差连接:
- 要求两个输入的形状相同,以便加法操作后输出张量的形状相同。
- 残差连接的核心优势:无损梯度反向传播。
- 因为Dropout的随机失活会阻断部分梯度路径,
- 而标准顺序确保残差连接始终保留原始输入X的梯度通路。
- 标准顺序:
- 残差输入x经过随机失活后,与子层输出y相加,相加后再经过层归一化(样本内所有特征经过归一化,即每个学生的所有科目成绩归一化)。
- 即 Dropout → 残差连接 → 层归一化
- 残差块:(x 线性值) + (y 残差路径输出 即高度非线性的特征)
- 对应这里代码中,传入层归一化的内容:self.dropout(Y) + X
python
# AddNorm模块使用示例
# 创建AddNorm实例:输入张量最后维度为4,Dropout概率0.5
add_norm = common.AddNorm([3, 4], 0.5)
add_norm.eval() # 切换至评估模式(关闭Dropout,BatchNorm使用移动平均)
# 创建输入数据:2个样本,每个样本3个位置,每个位置4维特征
input1 = torch.ones((2, 3, 4))
input2 = torch.ones((2, 3, 4)) # 残差连接输入
output = add_norm(input1, input2) #前向传播
print("输出形状验证(应与输入相同)\n"
"输出形状:", output.shape) # torch.Size([2, 3, 4])
7.4. 编码器
关键设计思想
- 残差连接:缓解梯度消失,支持深层网络训练
- 层归一化:稳定各层输入分布,加速收敛
- 位置编码:注入序列位置信息(替代RNN的时序特性)
- 多头注意力:并行捕获不同子空间信息
有了组成Transformer编码器的基础组件,现在可以先实现【编码器中的一个层】:
EncoderBlock类:包含两个子层- 多头自注意力
- 基于位置的前馈网络
- 这两个子层都使用了残差连接和紧随的层规范化(详情可看:7.3. 残差连接和层规范化)
EncoderBlock 结构
- 多头自注意力:Q=K=V=输入,实现自注意力机制
- AddNorm1:自注意力输出 与 原始输入进行残差连接+层归一化
- 前馈网络:逐位置独立处理(Position-wise)
- AddNorm2:前馈网络输出 与 前层输出进行残差连接+层归一化
python
class EncoderBlock(nn.Module):
""" Transformer编码器块
包含多头自注意力 + (残差连接+层归一化) + 前馈网络 + (残差连接+层归一化) """
def __init__(self, key_size, query_size, value_size, # qkv向量维度
num_hiddens, # 隐藏层维度
norm_shape, # 层归一化形状(通常为[seq_length, dim])
ffn_num_input, # 前馈网络输入维度(等于num_hiddens)
ffn_num_hiddens, # 前馈网络中间层维度
num_heads, # 多头注意力头数
dropout, use_bias=False, **kwargs): # 随机失活率,是否使用偏置项
super(EncoderBlock, self).__init__(**kwargs)
# 多头自注意力层(输入输出维度均为num_hiddens)
self.attention = MultiHeadAttention(
key_size, query_size, value_size, num_hiddens, num_heads, dropout,
use_bias)
self.addnorm1 = AddNorm(norm_shape, dropout) # 残差连接+层归一化模块一(处理自注意力输出)
self.ffn = PositionWiseFFN(
ffn_num_input, ffn_num_hiddens, num_hiddens) # 位置前馈网络(逐位置独立处理)
self.addnorm2 = AddNorm(norm_shape, dropout) # 残差连接+层归一化模块二(处理前馈网络输出)
def forward(self, X, valid_lens):
"""前向传播
X : 输入张量 [batch_size, seq_length, num_hiddens]
valid_lens: 有效长度掩码 [batch_size]
返回:处理后的张量 [batch_size, seq_length, num_hiddens]
"""
# 自注意力计算(Q=K=V=X,全连接自注意力)
# 输出形状:[batch_size, seq_length, num_hiddens]
attention_output = self.attention(X, X, X, valid_lens)
# 第一个残差连接+层归一化
# 公式:LayerNorm(X + Dropout(attention_output))
Y = self.addnorm1(X, attention_output)
# 前馈网络处理
# 公式:FFN(Y) = max(0, YW1+b1)W2+b2
ffn_output = self.ffn(Y)
# 第二个残差连接+层归一化
return self.addnorm2(Y, ffn_output)正如从代码中所看到的:
- Transformer编码器中的任何层都不会改变其输入的形状
python
# 测试代码(验证维度变换)
# 同时处理2个独立序列,序列包含100个时间步,每个时间步有24个特征
X = torch.ones((2, 100, 24)) # 模拟输入 [batch_size=2, seq_length=100, dim=24]
valid_lens = torch.tensor([3, 2]) # 有效长度掩码
# 创建编码器块
encoder_blk = common.EncoderBlock(24, 24, 24, 24, [100, 24], 24, 48, 8, 0.5)
encoder_blk.eval() # 设置为评估模式(关闭dropout等训练专用层)
output = encoder_blk(X, valid_lens)
print(f"编码器块输出形状:{output.shape}")
下面实现的Transformer编码器的代码中,堆叠了num_layers个EncoderBlock类的实例。
- 由于这里使用的是值范围在-1和1之间的固定位置编码,
- 因此通过学习得到的输入 的嵌入表示的值 需要先乘以嵌入维度的平方根进行重新缩放,然后再与位置编码相加。
TransformerEncoder 结构
- 词嵌入层:将词索引映射为向量,乘以sqrt(dim)进行缩放
- 位置编码:添加位置信息(正弦/余弦函数生成)
- 堆叠编码器块:多层EncoderBlock串联构成深度网络
维度变化说明
- 输入 :
[batch_size, seq_length]- 嵌入后 :
[batch_size, seq_length, num_hiddens]- 位置编码:
[batch_size, seq_length, num_hiddens]- 输出 :
[batch_size, seq_length, num_hiddens]有效长度处理
valid_lens用于屏蔽填充位置的注意力计算- 通过注意力权重掩码实现(softmax前将填充位置设为负无穷)
超参数作用
num_heads:多头注意力头数(分块并行计算)ffn_num_hiddens:前馈网络中间层维度(通常为4倍输入维度)dropout:随机失活概率(防止过拟合
python
class TransformerEncoder(Encoder):
"""Transformer编码器
包含嵌入层+位置编码+堆叠的编码器块 """
def __init__(self, vocab_size, # 词汇表大小
key_size, query_size, value_size, # qkv向量维度
num_hiddens, # 隐藏层维度
norm_shape, # 层归一化形状
ffn_num_input, ffn_num_hiddens, # 前馈网络的 输入维度 和 中间层维度
num_heads, # 多头注意力头数
num_layers, # 编码器块堆叠层数
dropout, use_bias=False, **kwargs): # 随机失活率,是否使用偏置项
super(TransformerEncoder, self).__init__(**kwargs)
self.num_hiddens = num_hiddens
# 词嵌入层(添加了dropout)
self.embedding = nn.Embedding(vocab_size, num_hiddens)
# 位置编码层(正弦/余弦函数生成)
self.pos_encoding = PositionalEncoding(num_hiddens, dropout)
# 堆叠的编码器块(Sequential形式)
self.blks = nn.Sequential()
for i in range(num_layers): # 共堆叠num_layers个编码器块
# 添加编码器块到Sequential
self.blks.add_module("block"+str(i), # 编码器块名字叫 block1~blockN
EncoderBlock(key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens,
num_heads, dropout, use_bias))
def forward(self, X, valid_lens, *args):
"""前向传播
X: 输入词序列 [batch_size, seq_length]
valid_lens: 有效长度掩码 [batch_size]
返回:编码后的张量 [batch_size, seq_length, num_hiddens]
"""
# 嵌入层处理(乘以sqrt(dim)进行缩放)
# 公式:Embedding(X) * sqrt(num_hiddens)
# 因为位置编码值在-1和1之间,因此嵌入值乘以嵌入维度的平方根进行缩放,
# 然后再与位置编码相加
embedded = self.embedding(X) * math.sqrt(self.num_hiddens)
# 位置编码(添加位置信息)
# 公式:X = embedded + PositionalEncoding(embedded)
X = self.pos_encoding(embedded)
self.attention_weights = [None] * len(self.blks) # 存储各层注意力权重
for i, blk in enumerate(self.blks): # 逐层处理
X = blk(X, valid_lens) # 数据流经过每个编码器块
# 保存每层注意力权重(用于可视化分析)
self.attention_weights[
i] = blk.attention.attention.attention_weights
return X下面指定超参数来创建一个两层的Transformer编码器:
- Transformer编码器输出的形状:(批量大小,时间步数目,
num_hiddens)
python
# 创建完整编码器
encoder = common.TransformerEncoder(
200, 24, 24, 24, 24, [100, 24], 24, 48, 8, 2, 0.5)
encoder.eval() # 设置为评估模式(关闭dropout等训练专用层)
output = encoder(torch.ones((2, 100), dtype=torch.long), valid_lens)
print(f"编码器输出形状:{output.shape}")
7.5. 解码器
关键设计思想
- 缓存机制:预测阶段保存已生成序列的表示,实现自回归解码
- 掩码自注意力:训练时通过dec_valid_lens掩码未来信息
- 残差连接:缓解梯度消失,支持深层网络训练
- 层归一化:稳定各层输入分布,加速收敛
如 图10.7.1所示,Transformer解码器也是由多个相同的层组成:
- 在
DecoderBlock类中实现的每个层包含了三个子层:- 解码器自注意力
- "编码器-解码器"注意力
- 基于位置的前馈网络
- 这些子层也都被残差连接和紧随的层规范化围绕。
DecoderBlock 结构
- 自注意力层:带掩码机制,防止看到未来信息(训练时使用递增有效长度)
- 编码器-解码器注意力层:K / V为 编码器输出,实现跨模态信息(原序列与目标序列)交互
- 前馈网络:逐位置独立处理(Position-wise)
- 三层残差连接+层归一化:分别对应三个子层
正如在本节前面所述,
- 在 掩蔽多头解码器自注意力层 (第一个子层)中,
- 查询、键 和 值:都来自上一个解码器层的输出
- 作用:防止解码时"偷看"未来信息
- 在 编码器-解码器注意力 中:
- 作用:连接编码器输出,实现跨序列关注
- 查询:前一解码器层的输出
- 键 / 值:编码器最终输出 (即 来自整个编码器的输出)
- 关于序列到序列模型 (sequence-to-sequence model),
- 训练阶段 :
- 输出序列的所有位置(时间步)的词元都已知
- → 所有词元皆同时处理
- 预测阶段 :
- 输出序列的词元为逐个生成
- → 所有词元逐个处理
- 因此,在任何解码器时间步中,只有生成的词元才能用于解码器的自注意力计算中。
- 为使 解码器中保留自回归属性,其掩蔽自注意力设定了参数
dec_valid_lens, - 以便任何查询都只会与解码器中所有已经生成词元的位置(即直到该查询位置为止)进行注意力计算。
- 训练阶段 :
| 阶段 | 输入处理 | 缓存使用 | 掩码机制 |
|---|---|---|---|
| 训练 | 批量并行处理 即:同时处理整个序列的所有时间步 | 无需缓存 训练时:通常接收 完整的输入序列(如源语言句子) 和 对应的完整目标序列(如目标语言翻译), 因此不需要缓存历史状态, 因为每个时间步的输入都是完整的序列。 | 递增掩码 (防窥) |
| 推理 | 逐词生成 即:逐个时间步生成词元, 因此需要排队处理 | 拼接历史缓存 (减少重复计算) 历史缓存:最开始的提示词 与 历史生成词元 拼接而成的 最新的完整上下文 | 无 (缓存已隐含时序) |
| 阶段 | 输入来源 | 缓存作用 | 目标 |
|---|---|---|---|
| 训练 | 完整目标序列(教师强制) | 无需缓存(或仅用隐藏状态) | 优化模型参数 |
| 预测 | 模型自身生成的词元 | 缓存历史词元作为上下文 | 逐步生成合理序列 |
- 训练时 :采用教师强制 (Teacher Forcing)策略(提供真实词元,无需依赖模型自身生成)
- 即 每次预测下一个词元时,直接使用目标序列中对应的真实词元作为输入 ,而非模型自身生成的词元。例如:
- 预测第2个词元时,输入是第1个真实词元 "我"(而非模型生成的词元)。
- 预测第3个词元时,输入是第2个真实词元 "爱"。
- 即 每次预测下一个词元时,直接使用目标序列中对应的真实词元作为输入 ,而非模型自身生成的词元。例如:
python
class DecoderBlock(nn.Module):
"""解码器中第i个块"""
def __init__(self, key_size, query_size, value_size, # qkv向量维度
num_hiddens, # 隐藏层维度
norm_shape, # 层归一化形状
ffn_num_input, ffn_num_hiddens, # 前馈网络的 输入维度 和 中间层维度
num_heads, # 多头注意力头数
dropout, i, **kwargs): # 随机失活率,解码器层索引(用于缓存管理)
super(DecoderBlock, self).__init__(**kwargs)
self.i = i # 记录当前解码器层索引
# 自注意力层:掩蔽多头注意力(带掩码机制防止看到未来信息)
self.attention1 = MultiHeadAttention(
key_size, query_size, value_size, num_hiddens, num_heads, dropout)
self.addnorm1 = AddNorm(norm_shape, dropout) # 第一个残差连接+层归一化
# 编码器-解码器注意力层(使用编码器输出作为K/V)
self.attention2 = MultiHeadAttention(
key_size, query_size, value_size, num_hiddens, num_heads, dropout)
self.addnorm2 = AddNorm(norm_shape, dropout) # 第二个残差连接+层归一化
# 位置前馈网络
self.ffn = PositionWiseFFN(ffn_num_input, ffn_num_hiddens,
num_hiddens)
self.addnorm3 = AddNorm(norm_shape, dropout) # 第三个残差连接+层归一化
def forward(self, X, state):
"""前向传播
X: 输入张量 [batch_size, seq_length, num_hiddens]
state: 包含3个元素的列表
[0] enc_outputs : 编码器输出
[1] enc_valid_lens: 编码器有效长度
[2] cached_states : 各层缓存状态列表
返回:处理后的张量及更新后的state
"""
# 提取状态信息
# 编码器输出是只有 编码后的张量
enc_outputs, enc_valid_lens = state[0], state[1]
# 训练阶段:输出序列的所有词元都在同一时间处理,
# 因此state[2][self.i]初始化为None
# 预测阶段:输出序列是通过词元一个接着一个解码的,
# 因此state[2][self.i]包含着直到当前时间步第i个块解码的输出表示
# state[2] 各层缓存状态合集,state[2][i] 第i层解码器块的缓存
# 缓存管理:存储历史计算状态来避免重复计算,提升推理效率
# 训练时:每次重新计算(训练时每个批次处理整个目标序列,因此无需缓存历史状态,因为每个时间步的输入皆完整序列)
# 预测时:使用缓存。逐词生成,需拼接历史缓存state[2][self.i] 和 当前输入X,形成新的完整上下文
# 首次预测时,只有提示词,即首个当前输入
if state[2][self.i] is None: # 训练阶段或预测首次计算
key_values = X # 直接使用当前输入X作为初始缓存
else: # 预测阶段(非首次)
# 历史缓存(state[2][self.i])与 当前输入X沿序列维度(axis=1)拼接
key_values = torch.cat((state[2][self.i], X), axis=1)
state[2][self.i] = key_values # 更新缓存
# 训练阶段:生成有效长度掩码(递增序列),用于屏蔽未来信息
if self.training:
# 解码:批次数 和 序列长度/时间步,特征维度使用占位符
batch_size, num_steps, _ = X.shape
# dec_valid_lens的开头:(batch_size,num_steps),
# 其中每一行是[1,2,...,num_steps]
# .repeat()调整为列向量形式
dec_valid_lens = torch.arange(
1, num_steps + 1, device=X.device).repeat(batch_size, 1)
else: # 推理时:无需掩码(因缓存已隐含时序)
dec_valid_lens = None # 预测阶段不需要
# 自注意力层:掩蔽多头注意力(带掩码)
# qkv皆来自上一解码器层的输出(q为上一层解码器层输出,kv
# 预测时为拼接后的缓存,即 包含历史所有时间步的键值对;训练时为完整键值对,但是经过防窥掩码后的键值对)
# 公式:Attention(Q=X, K=key_values, V=key_values)
X2 = self.attention1(X, key_values, key_values, dec_valid_lens)
Y = self.addnorm1(X, X2) # 残差连接+层归一化
# 编码器-解码器注意力:q来自上一解码层的输出,kv来自整个编码器的输出
# 公式:Attention(Q=Y, K=enc_outputs, V=enc_outputs)
# enc_outputs的开头:(batch_size,num_steps,num_hiddens)
Y2 = self.attention2(Y, enc_outputs, enc_outputs, enc_valid_lens)
Z = self.addnorm2(Y, Y2) # 残差连接+层归一化
# 前馈网络处理
return self.addnorm3(Z, self.ffn(Z)), state为便于在"编码器-解码器"注意力中进行缩放点积计算和残差连接中进行加法计算,
- 编码器 和 解码器 的特征维度 皆为
num_hiddens
python
# 创建编码器块
encoder_blk = common.EncoderBlock(24, 24, 24, 24, [100, 24], 24, 48, 8, 0.5)
encoder_blk.eval() # 设置为评估模式(关闭dropout等训练专用层)
# 创建解码器块
decoder_blk = common.DecoderBlock(24, 24, 24, 24, [100, 24], 24, 48, 8, 0.5, 0)
decoder_blk.eval() # 设置为评估模式(关闭dropout等训练专用层)
# 同时处理2个独立序列,序列包含100个时间步,每个时间步有24个特征
X = torch.ones((2, 100, 24)) # 模拟输入 [batch_size=2, seq_length=100, dim=24]
valid_lens = torch.tensor([3, 2]) # 有效长度掩码
state = [encoder_blk(X, valid_lens), valid_lens, [None]] # 构建解码器状态
output = decoder_blk(X, state) # 前向传播
print(f"解码器块输出,第一个批次的形状:{output[0].shape}") # torch.Size([2, 100, 24])
- 现在已构建了由
num_layers个DecoderBlock实例组成的完整的Transformer解码器。 - 最后,通过一个全连接层计算所有
vocab_size个可能的输出词元的预测值。 - 解码器的以下两种数据都被存储下来,以便可以日后可视化:
- 自注意力权重
- 编码器-解码器注意力权重
TransformerDecoder 结构
- 词嵌入层:将词索引映射为向量,乘以sqrt(dim)进行缩放
- 位置编码:添加序列位置信息(正弦/余弦函数)
- 堆叠解码器块:多层DecoderBlock串联构成深度网络
- 输出层:全连接层映射到词表维度
维度变化说明
- 输入 :
[batch_size, seq_length]- 嵌入后 :
[batch_size, seq_length, num_hiddens]- 位置编码:
[batch_size, seq_length, num_hiddens]- 输出 :
[batch_size, seq_length, vocab_size](解码器最终输出)注意力权重存储
self._attention_weights[0]:存储各层自注意力权重self._attention_weights[1]:存储各层编码器-解码器注意力权重状态管理
- 训练阶段:每次重新计算,无状态缓存
- 预测阶段:使用缓存保存已生成序列的表示,实现增量解码
python
class TransformerDecoder(AttentionDecoder):
"""Transformer解码器:包含嵌入层+位置编码+堆叠的解码器块+输出层"""
def __init__(self, vocab_size, # 词汇表大小
key_size, query_size, value_size, # qkv向量维度
num_hiddens, # 隐藏层维度
norm_shape, # 层归一化形状
ffn_num_input, ffn_num_hiddens, # 前馈网络的 输入维度 和 中间层维度
num_heads, # 多头注意力头数
num_layers, # 解码器块堆叠层数
dropout, **kwargs):
super(TransformerDecoder, self).__init__(**kwargs)
self.num_hiddens = num_hiddens
self.num_layers = num_layers
# 词嵌入层
self.embedding = nn.Embedding(vocab_size, num_hiddens)
# 位置编码层(正弦/余弦函数生成)
self.pos_encoding = PositionalEncoding(num_hiddens, dropout)
# 堆叠的解码器块(使用顺序容器)
self.blks = nn.Sequential()
for i in range(num_layers): # 共堆叠num_layers个解码器块
self.blks.add_module("block"+str(i), # 添加解码器块到容器内
DecoderBlock(key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens,
num_heads, dropout, i))
# 输出层(将隐藏层映射到词表维度)
self.dense = nn.Linear(num_hiddens, vocab_size)
def init_state(self, enc_outputs, enc_valid_lens, *args):
"""初始化解码器状态
enc_outputs: 编码器输出
enc_valid_lens: 编码器有效长度
返回:状态元组 [enc_outputs, enc_valid_lens, [None]*num_layers]
"""
# [None]*num_layers是将n层解码器块的 缓存状态列表都先初始化为None
return [enc_outputs, enc_valid_lens, [None] * self.num_layers]
def forward(self, X, state):
"""前向传播
X: 输入词序列 [batch_size, seq_length]
state: 解码器状态
返回:输出概率分布及更新后的state
"""
# 嵌入层处理(乘以sqrt(dim)进行缩放)
# 位置编码值在-1和1之间,因此嵌入值乘以嵌入维度的平方根进行缩放
# 然后再.pos_encoding()与位置编码相加
X = self.pos_encoding(self.embedding(X) * math.sqrt(self.num_hiddens))
# 存储注意力权重(用于可视化)
self._attention_weights = [[None] * len(self.blks) for _ in range (2)]
for i, blk in enumerate(self.blks): # 逐层处理
# state: [编码器输出,编码器有效长度,各层缓存状态列表]
X, state = blk(X, state) # 当前层解码器块的输出:处理后的张量&更新后的state
# 自注意力权重:解码器自注意力权重
self._attention_weights[0][
i] = blk.attention1.attention.attention_weights
# "编码器-解码器"自注意力权重
self._attention_weights[1][
i] = blk.attention2.attention.attention_weights
# 输出层(全连接层+softmax在外部处理)
return self.dense(X), state
@property
def attention_weights(self):
"""获取注意力权重
[0] 自注意力权重:解码器自注意力权重
[1] "编码器-解码器"自注意力权重
"""
return self._attention_weights7.6. 训练
- 依照Transformer架构来实例化编码器-解码器模型。
- 指定Transformer的编码器和解码器都是2层,都使用4头注意力。
- 与 (现代循环神经网络------动手学深度学习9-CSDN博客7. 序列到序列学习(seq2seq)7.4. 训练)类似,
- 为了进行序列到序列的学习,
- 下面在"英语-法语"机器翻译数据集上训练Transformer模型:
python
# 下载器与数据集配置
# 为 time_machine 数据集注册下载信息,包括文件路径和校验哈希值(用于验证文件完整性)
downloader = common.C_Downloader()
DATA_HUB = downloader.DATA_HUB # 字典,存储数据集名称与下载信息
DATA_URL = downloader.DATA_URL # 基础URL,指向数据集的存储位置
# 注册数据集信息到DATA_HUB全局字典
# 格式:(数据集URL, MD5校验值)
DATA_HUB['fra-eng'] = (DATA_URL + 'fra-eng.zip', # 完整下载URL(DATA_URL是d2l定义的基准URL)
'94646ad1522d915e7b0f9296181140edcf86a4f5') # 文件MD5,用于校验下载完整性
python
# 配置超参数
num_hiddens = 32 # 隐藏层维度(Transformer特征维度)
num_layers = 2 # 编码器/解码器堆叠层数
dropout = 0.1 # 随机失活概率(防止过拟合)
batch_size = 64 # 训练批次大小
num_steps = 10 # 序列最大长度(防止过长序列)
lr = 0.005 # 学习率(Adam优化器)
num_epochs = 200 # 训练轮次
device = common.try_gpu() # 自动选择GPU/CPU
# 前馈网络参数
ffn_num_input = 32 # 前馈网络输入维度(等于num_hiddens)
ffn_num_hiddens = 64 # 前馈网络中间层维度(通常为4倍输入维度)
num_heads = 4 # 多头注意力头数
# 注意力机制参数
key_size = query_size = value_size = 32 # K/Q/V向量维度
norm_shape = [32] # 层归一化维度(与num_hiddens一致)
# 加载机器翻译数据集(中英翻译示例)
# 返回:数据迭代器、源语言词汇表、目标语言词汇表
train_iter, src_vocab, tgt_vocab = common.load_data_nmt(downloader, batch_size, num_steps)
# 构建Transformer编码器
encoder = common.TransformerEncoder(
vocab_size=len(src_vocab), # 源语言词汇表大小
key_size=key_size, # 键向量维度
query_size=query_size, # 查询向量维度
value_size=value_size, # 值向量维度
num_hiddens=num_hiddens, # 隐藏层维度
norm_shape=norm_shape, # 层归一化形状
ffn_num_input=ffn_num_input, # 前馈网络输入维度
ffn_num_hiddens=ffn_num_hiddens, # 前馈网络中间层维度
num_heads=num_heads, # 多头注意力头数
num_layers=num_layers, # 编码器层数
dropout=dropout # 随机失活概率
)
# 构建Transformer解码器
decoder = common.TransformerDecoder(
vocab_size=len(tgt_vocab), # 目标语言词汇表大小
# 其他参数与编码器配置一致
key_size=key_size,
query_size=query_size,
value_size=value_size,
num_hiddens=num_hiddens,
norm_shape=norm_shape,
ffn_num_input=ffn_num_input,
ffn_num_hiddens=ffn_num_hiddens,
num_heads=num_heads,
num_layers=num_layers,
dropout=dropout
)
# 组合编码器-解码器架构
net = common.EncoderDecoder(encoder, decoder)
# 训练序列到序列模型
# 模型,训练数据迭代器,学习率,训练轮次,目标语言词汇表(用于评估),训练设备
common.train_seq2seq(net, train_iter, lr, num_epochs, tgt_vocab, device)
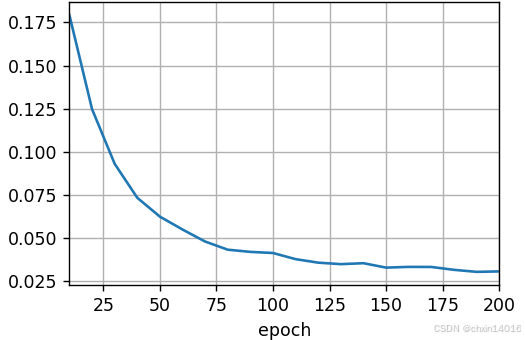
训练结束后,使用Transformer模型 将一些英语句子翻译成法语,并且计算它们的BLEU分数:
python
# 英法对照测试集
engs = ['go .', "i lost .", 'he\'s calm .', 'i\'m home .']
fras = ['va !', 'j\'ai perdu .', 'il est calme .', 'je suis chez moi .']
for eng, fra in zip(engs, fras): # 逐句进行机器翻译并评估
# 预测翻译结果(包含注意力权重序列)
translation, dec_attention_weight_seq = common.predict_seq2seq(
net, # 训练好的seq2seq模型
eng, # 待翻译的英文句子
src_vocab, # 源语言词汇表
tgt_vocab, # 目标语言词汇表
num_steps, # 最大序列长度
device, # 计算设备(GPU/CPU)
True # 返回注意力权重
)
# 计算BLEU-2分数(双语评估替手)
print(f'{eng} => {translation}, ',
f'bleu {common.bleu(translation, fra, k=2):.3f}')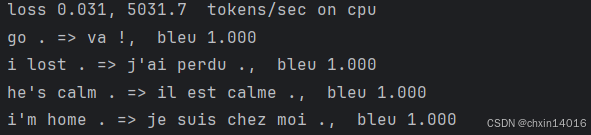
- 当进行最后一个英语到法语的句子翻译工作时,让我们可视化Transformer的注意力权重。
- 编码器自注意力权重的形状为
- (编码器层数,注意力头数,
num_steps或查询的数目,num_steps或"键-值"对的数目)
- (编码器层数,注意力头数,
python
# 提取编码器各层注意力权重
enc_attention_weights = torch.cat(net.encoder.attention_weights, 0) # 拼接所有层
print(f"(原来的)编码器注意力权重:{enc_attention_weights.shape}")
enc_attention_weights = enc_attention_weights.reshape((
num_layers, # 2层编码器
num_heads, # 4个注意力头
-1, # 自动计算维度(源序列长度)
num_steps # 目标序列长度
))
print(f"(重塑后)编码器注意力权重:{enc_attention_weights.shape}")
- 在编码器的自注意力中,QK皆来自相同的输入序列。
- 因为填充词元是不携带信息的,因此通过指定输入序列的有效长度可以避免查询与使用填充词元的位置计算注意力。
- 下面逐行呈现两层多头注意力的权重。
- 每个注意力头都根据QKV的不同的表示子空间 来表示不同的注意力。
python
# 可视化编码器自注意力热图
common.show_heatmaps(
enc_attention_weights.cpu(), # 转为CPU张量[2行(编码器层数),4列(注意力头数),Q,K]
xlabel='Key positions', # 横轴:键位置
ylabel='Query positions', # 纵轴:查询位置
titles=['Head %d' % i for i in range(1, 5)], # 4个头的标题
figsize=(7, 3.5) # 图像尺寸
)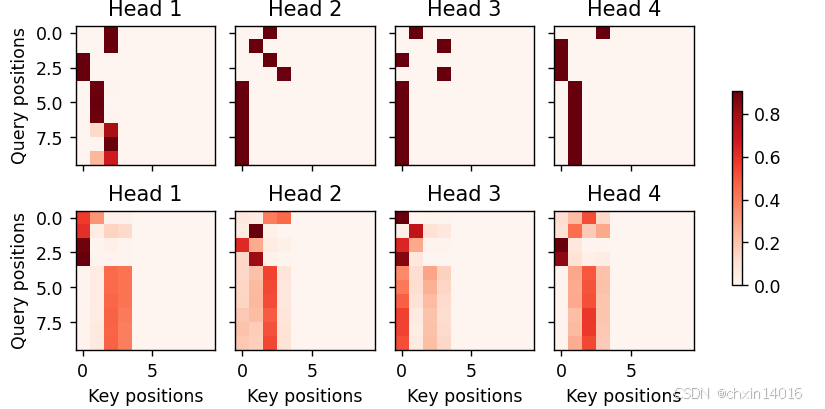
为了可视化:
- 解码器的自注意力权重 和
- "编码器-解码器"的注意力权重
则需完成更多的数据操作工作:例如用零填充被掩蔽住的注意力权重。
- 注意:解码器的自注意力权重 和**"编码器-解码器"的注意力权重** 都有相同的查询 :
- 即 以序列开始词元(beginning-of-sequence,BOS)打头,再与后续输出的词元共同组成序列。
python
# 解码器注意力权重处理:将多维度注意力权重转换为可视化友好的5D张量
# 二维列表构建:按 时间步、层、注意力类型、头展开权重
dec_attention_weights_2d = [head[0].tolist() # 将每个头的权重矩阵 转换为Python列表
for step in dec_attention_weight_seq # 遍历时间步(每个时间步对应一个解码器输出位置)
for attn in step # 遍历解码器层(attn:每层的注意力数据)(每个时间步包含所有层的注意力数据)
for blk in attn # 遍历注意力类型(blk:自注意力/交叉注意力)
for head in blk] # 遍历注意力头(每个注意力类型下的所有头)
# 此时数据结构:二维列表 [总样本数, 序列长度],每个元素是某个头在某个位置上的权重矩阵
# 转换为DataFrame并填充缺失值
# pd.DataFrame()从二维列表到 DataFrame,为后续的fillna() 提供结构化操作接口
# 缺失值处理:fillna(0.0)将 缺失值NaN 填充为 0
# DataFrame.values 转换为 NumPy数组:跨库数据桥接
# torch.tensor() 转换为 PyTorch 张量:适配深度学习框架
dec_attention_weights_filled = torch.tensor(
pd.DataFrame(dec_attention_weights_2d)
.fillna(0.0)
.values) # 类型变化:DataFrame → NumPy数组 → 张量
# 重塑为5维张量:[时间步, 2种类型, 层数, 头数, 序列长度]
# 类型维度:0=自注意力,1=交叉注意力
dec_attention_weights = (dec_attention_weights_filled
.reshape((-1, 2, num_layers, num_heads, num_steps)))
# 分离两种注意力类型
# 通过维度置换调整张量存储顺序,便于按注意力类型切片
# permute原理:将原维度索引[0,1,2,3,4]映射到新顺序[1,2,3,0,4],实现注意力类型的分离
# 新维度:[类型, 层, 头, 时间步, 序列长度]
dec_self_attention_weights, dec_inter_attention_weights = \
dec_attention_weights.permute(1, 2, 3, 0, 4) # 调整维度顺序
# 打印维度确认
print(f"自注意力:\n{dec_self_attention_weights.shape}")
print(f"交叉注意力:\n{dec_inter_attention_weights.shape}")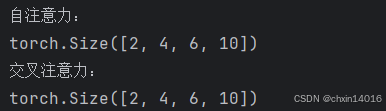
由于解码器自注意力的自回归属性,查询不会对当前位置之后的"键-值"对进行注意力计算。
python
# Plusonetoincludethebeginning-of-sequencetoken
# 可视化解码器自注意力热图(包含起始符<BOS>)
# 分词:translation.split() 将字符串分割为单词列表
common.show_heatmaps(
dec_self_attention_weights[:, :, :, :len(translation.split()) + 1], # +1包含起始符
xlabel='Key positions', ylabel='Query positions',
titles=['Head %d' % i for i in range(1, 5)], figsize=(7, 3.5))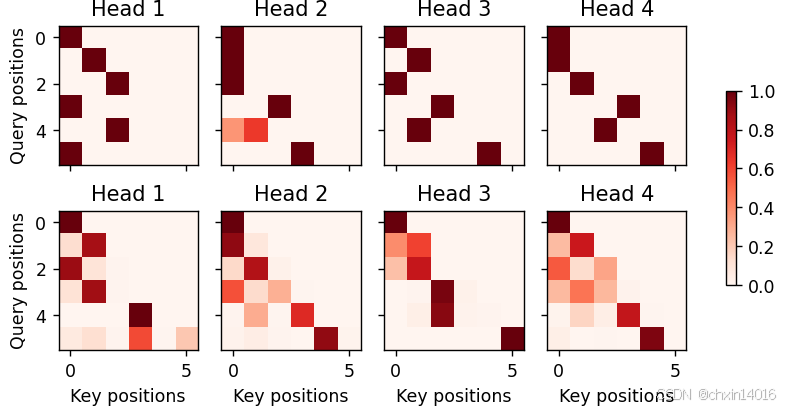
- 与编码器的自注意力的情况类似:
- 通过 指定输入序列的有效长度,
- 输出序列的查询 不会与输入序列中 填充位置的词元进行注意力计算。
python
# 可视化解码器交叉注意力热图(编码器-解码器)
common.show_heatmaps(
dec_inter_attention_weights, xlabel='Key positions',
ylabel='Query positions', titles=['Head %d' % i for i in range(1, 5)],
figsize=(7, 3.5))
# 交叉注意力核心:展示解码器如何关注编码器输出的不同位置
plt.pause(4444) # 间隔的秒数: 4s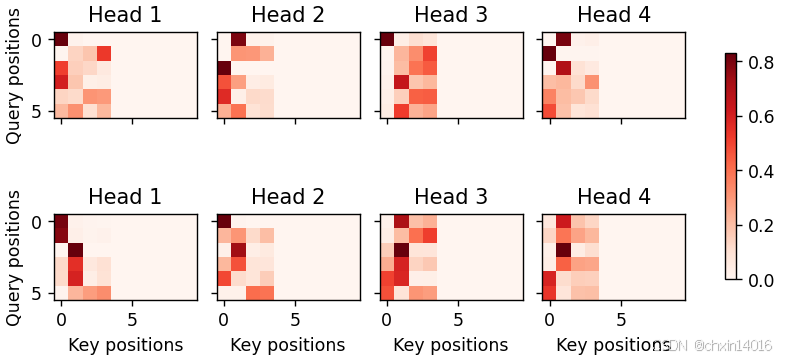
- 尽管Transformer架构是为了序列到序列 的学习而提出的,但正如本书后面将提及的那样:
- Transformer编码器 或 Transformer解码器通常被单独用于不同的深度学习任务中。
小结
Transformer是编码器-解码器架构的一个实践,尽管在实际情况中编码器或解码器可以单独使用。
在Transformer中,多头自注意力用于表示输入序列和输出序列,不过解码器必须通过掩蔽机制来保留自回归属性。
Transformer中的残差连接 和层规范化是训练非常深度模型的重要工具。
Transformer模型中:
基于位置的前馈网络 使用同一个多层感知机,
作用:对所有序列位置的表示进行转换。