题目
https://leetcode.cn/problems/remove-zero-sum-consecutive-nodes-from-linked-list/
思路
题目要删除链表中所有总和为0的连续节点,也就是说,如果找到一个总和为0,当删除之后,会发现新的连续节点又可以拼接成0,所以要反复删,直到没有这样的序列为止。
我一开始想到的是,用暴力法,就是不断遍历链表,每次找到一个和为0的子序列就删掉,然后重新开始... 但这样的话,最坏情况可能要扫描很多次
更好的思路就是,前缀和的思路,如果我从头开始累加每个节点的值,得到一个前缀和序列。关键点:如果两个位置的前缀和相同,说明它们之间的那段链表的和就是0。
比如说:
链表: 1 → 2 → -3 → 3→ 1
前缀: 1 → 3 → 0 → 3→ 4
第2个节点和第4个节点的前缀和都是3,那2到3之间的 `-3→3` 这一段和就是0。
具体的实现步骤:
- 第一次遍历,我用一个哈希表来记录每个前缀和对应的节点位置。关键是,如果遇到相同的前缀和,就更新它,保留最后一次出现的位置。
比如刚才那个例子,前缀和3出现了两次,我就记录最后那个位置。
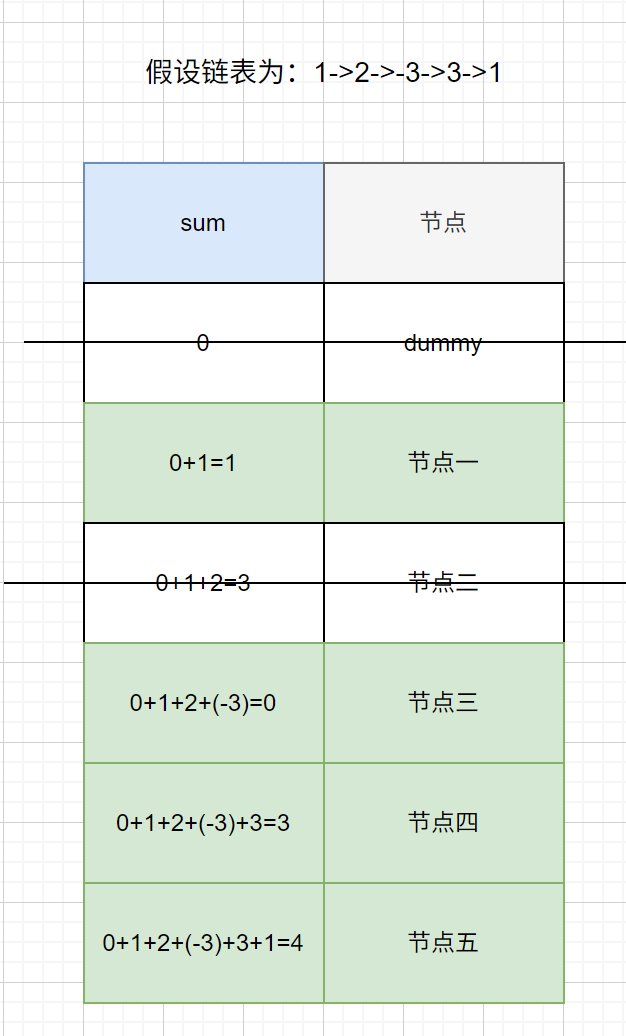
- 第二次遍历,我再扫一遍,计算前缀和,然后直接让当前节点的 `next` 指向哈希表中记录的"相同前缀和位置"的下一个节点。这样就相当于把中间和为0的那一段给跳过去了
为什么要保留"最后一次"出现的位置呢?
如果有多个重叠的和为0的子序列,保留最后一次出现的位置,可以让我们一次性跳过所有这些重叠的部分,就是贪心的思想。
举个例子:1 → -1 → 2 → -2 → 3
前缀和在3个位置都是0(初始、第2个节点后、第4个节点后),如果我只记录最后那个位置,第二次遍历时就可以从 dummy 直接跳到最后的3,一次性把前面所有和为0的都删掉了。
时间复杂度是 O(n),因为就遍历了两次链表。空间复杂度也是 O(n),因为哈希表最多存 n 个不同的前缀和。
还有一个小细节,需要创建一个 dummy 虚拟头节点,因为头节点本身也可能被删除,用 dummy 可以统一处理。
过程
链表: 1 → 2 → -3 → 3 → 1
第一次遍历后得到的哈希表:
prefixSum[0] = node(-3) // 从dummy到-3,和为0
prefixSum[1] = node(1) // 第一个节点
prefixSum[3] = node(3) // 覆盖了之前的node(2)
prefixSum[4] = node(1) // 最后一个节点
第二次遍历开始:
轮次1:从 dummy 开始
当前位置: dummy
当前前缀和 sum = 0
我去哈希表里查:prefixSum[0] = node(-3)
操作: dummy->next = prefixSum[0]->next
dummy->next = node(-3)->next
dummy->next = node(3)
也就是说
-
dummy 原本指向 node(1)
-
现在改为指向 node(3)
-
跳过了 1→2→-3 这三个节点!
调整前: dummy → 1 → 2 → -3 → 3 → 1
调整后: dummy ─────────────→ 3 → 1
(跳过了和为0的部分)
然后 `current = current->next`,也就是 current 来到 node(3)
轮次2:从 node(3) 开始
当前位置: node(3)
当前前缀和 sum = 0 + 3 = 3
我去哈希表里查:prefixSum[3] = node(3),发现prefixSum[3] 是 node(3) 本身
因为第一次遍历时:
-
node(2) 的前缀和是 3,记录了 `prefixSum[3] = node(2)`
-
node(3) 的前缀和也是 3,**覆盖了**,记录 `prefixSum[3] = node(3)`
这说明从 node(2) 的下一个到 node(3) 之间(也就是-3→3)和为0!
操作: node(3)->next = prefixSum[3]->next
node(3)->next = node(3)->next
node(3)->next = node(1)
这次没有跳过任何东西,因为 `prefixSum[3]` 就是自己,指向自己的 next 就是保持原样。
然后 `current = current->next`,也就是 current 来到 node(1)
轮次3:从 node(1) 开始
当前位置: node(1) (最后一个)
当前前缀和 sum = 3 + 1 = 4
我去哈希表里查:prefixSum[4] = node(1)
操作: node(1)->next = prefixSum[4]->next
node(1)->next = node(1)->next
node(1)->next = nullptr
保持原样,然后 `current = current->next = nullptr`,循环结束
最终结果:dummy → 3 → 1
返回 `dummy->next` 也就是 `node(3)`
第二次遍历的本质:
对于每个节点,都问自己一个问题:"在第一次遍历中,和我有相同前缀和的最远节点是谁?"
然后直接跳到那个最远节点的下一个位置!
为什么这样能删除所有和为0的子序列?
因为第一次遍历已经帮我们"标记"好了所有的跳跃终点。
如果从位置A到位置B的前缀和相同:
→ 说明A的下一个到B之间的和为0
→ 第一次遍历记录 prefixSum[x] = B (最远的B)
→ 第二次遍历让A直接跳到B的下一个
→ 中间和为0的部分就被跳过了!
正确写法
cpp
class Solution {
public:
ListNode* removeZeroSumSublists(ListNode* head) {
ListNode* dummy = new ListNode(0);
dummy->next = head;
int sum = 0;
unordered_map<int,ListNode*> prefixSum;
prefixSum[0] = dummy;
ListNode* current = head;
while(current)
{
sum += current->val;
prefixSum[sum] = current;
current = current->next;
}
sum = 0;
current = dummy;
while(current)
{
sum += current->val;
current->next = prefixSum[sum] ->next;
current = current->next;
}
ListNode* newHead = dummy->next;
delete dummy;
return newHead;
}
};