泊松分布是统计学中一个非常重要的离散型概率分布,尤其适合描述稀有事件的发生概率。
(一)什么是泊松分布
泊松分布描述的是在一段固定时间或空间内 ,某个稀有事件 发生的次数的概率分布。
例如:高速公路上的一个加油站,一小时内到达加油站的车辆数。一天内某网站收到的请求错误数。小区楼下的煎饼摊,一天可以卖出的煎饼数。一段固定时间内接到客服电话的次数。
(二)核心特征与假设
泊松过程需要满足以下条件:
1.独立性:事件的发生是相互独立的。一个事件的发生不影响另一个事件发生的概率。
2.平稳性 :在任意等长的时间/空间区间内,事件发生的平均速率(强度)是恒定 的。这个平均发生率记为 λ。
3.普通性:在极短的时间或空间内,发生两次或以上事件的概率趋近于零。即同一时刻最多发生一个事件,默认客服电话是一个一个打进来的、到达加油站的车也是一辆接一辆进来的。
(三)概率分布
如果随机变量 X(表示给定区间内事件发生的次数)服从泊松分布,我们记为:
X ~ Poisson(λ)
那么,在区间内事件恰好发生 k次的概率由以下概率质量函数 给出:
P(X = k) = (λ^k * e^(-λ)) / k!
其中:
P(X = k): 表示事件恰好发生 k 次的概率。
λ : 单位时间(或单位空间)内事件发生的平均次数(λ > 0)。这是泊松分布的唯一参数。
e: 自然对数的底数,约等于 2.71828。
k: 事件发生的次数(k = 0, 1, 2, ...)。
(四)分布数字特征
期望值(均值) : E(X) = λ
方差 : Var(X) = λ
泊松分布一个非常重要的特性是:它的期望和方差相等。这个特性在实际中常被用来初步判断一个数据集是否可能服从泊松分布。
(五)与二项分布的关系
当二项分布的试验次数 n很大,而成功概率 p很小时,二项分布可以近似用泊松分布来替代,其中 λ = n * p。
当 n > 20且 p < 0.05,或 n > 100且 np < 10时,这种近似效果很好。
为什么有用? : 当 n很大时,计算二项系数 C(n, k)会相对困难,而泊松分布公式更易于计算。
例如: 已知某种疾病的患病率为 0.001。在 5000 人的社区中,患病人数为 4 的概率是多少?
二项分布精确解 : X ~ Binomial(5000, 0.001), P(X=4) = C(5000, 4) * (0.001)^4 * (0.999)^4996,计算复杂。
泊松近似 : λ = 5000 * 0.001 = 5, X ~ Poisson(5), P(X=4) = (5^4 * e^(-5)) / 4!,计算简单,且结果非常接近。
(六)注意事项
λ 是常数: 必须确保事件发生的平均速率 λ 在观察期间是恒定的。例如,不能用"一天"的平均通话量来精确计算"凌晨3点-4点"的通话量,因为速率在一天内是变化的。
事件独立性: 这是关键假设。例如,一个地方发生地震后可能会引发余震(不独立),因此严格来说,地震次数不完全服从泊松分布。
均值等于方差: 如果你的数据计数的方差远大于或远小于均值(称为过离散或欠离散),那么数据可能不适用于泊松分布,需要考虑负二项分布等其他模型。
区间选择: λ 的大小依赖于你所选的时间或空间区间。例如,λ=3次/小时 等价于 λ=0.05次/分钟。
(七)Python计算
在Python中,可以使用 scipy.stats模块的 poisson对象来进行相关数值计算。
假设某咖啡店每小时平均有5位顾客通过手机下单(λ=5)。
python
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
# 定义参数 lambda
lambda_ = 5
# 1. 计算概率质量函数 - 恰好有 k 个订单的概率
k = 3
prob_exactly_3 = poisson.pmf(k, lambda_)
print(f"一小时恰好有 {k} 个订单的概率: {prob_exactly_3:.4f}") # 输出: 0.1404
# 2. 计算累积分布函数 - 订单数小于等于 k 的概率
k = 7
prob_at_most_7 = poisson.cdf(k, lambda_)
print(f"一小时订单数小于等于 {k} 的概率: {prob_at_most_7:.4f}") # 输出: 0.8666
# 3. 计算生存函数(1 - CDF) - 订单数大于 k 的概率
k = 2
prob_more_than_2 = poisson.sf(k, lambda_) # 等价于 1 - poisson.cdf(k, lambda_)
print(f"一小时订单数大于 {k} 的概率: {prob_more_than_2:.4f}") # 输出: 0.8753
# 4. 从泊松分布中生成随机数
random_samples = poisson.rvs(lambda_, size=100)
print(f"生成的100个随机样本的前10个: {random_samples[:10]}")
# 5. 绘制概率质量函数图
k_values = np.arange(0, 15) # k 从 0 到 14
pmf_values = poisson.pmf(k_values, lambda_)
plt.figure(figsize=(10, 6))
plt.bar(k_values, pmf_values, color='skyblue', alpha=0.7)
plt.axvline(lambda_, color='red', linestyle='--', label=f'λ (均值) = {lambda_}')
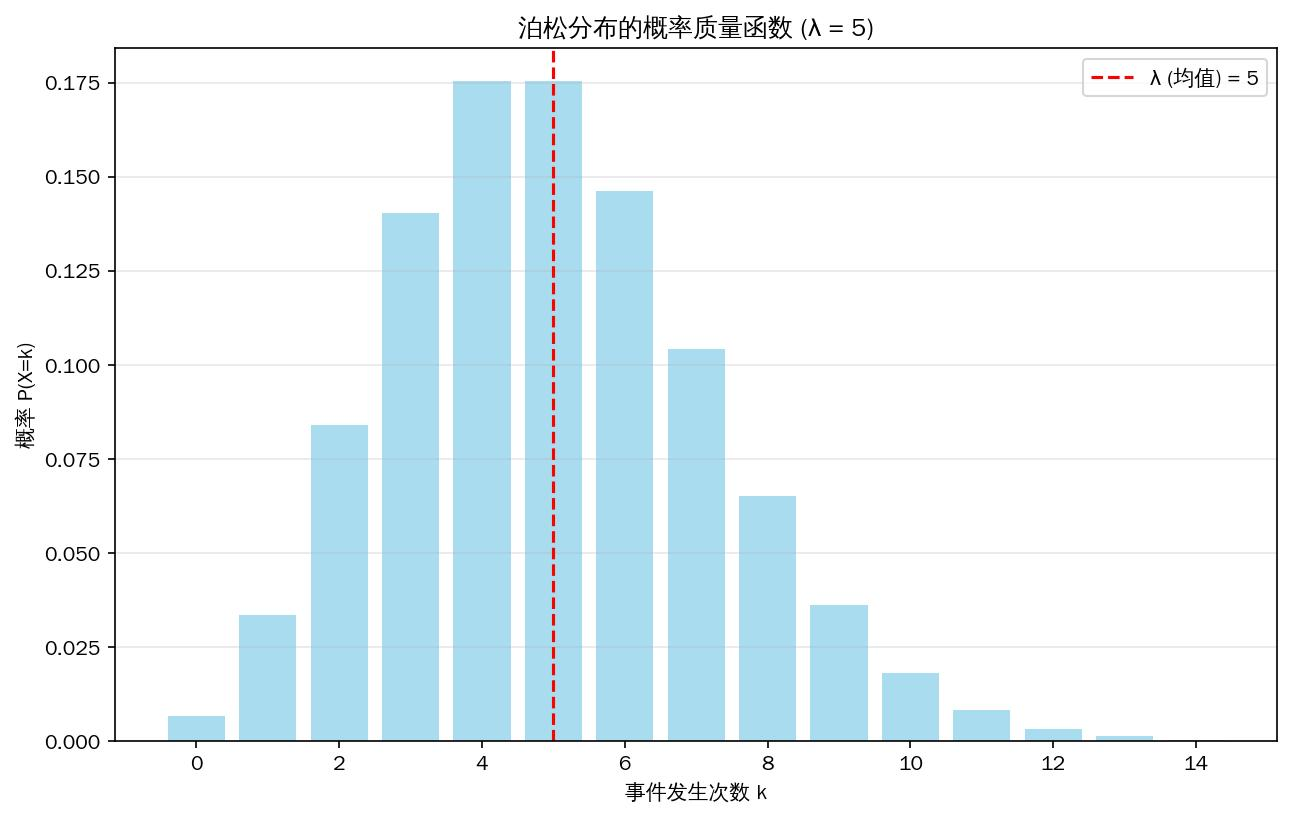
plt.title(f'泊松分布的概率质量函数 (λ = {lambda_})')
plt.xlabel('事件发生次数 k')
plt.ylabel('概率 P(X=k)')
plt.legend()
plt.grid(axis='y', alpha=0.3)
plt.show()输出:
一小时恰好有 3 个订单的概率: 0.1404
一小时订单数小于等于 7 的概率: 0.8666
一小时订单数大于 2 的概率: 0.8753
生成的100个随机样本的前10个: [4 5 2 6 8 4 5 5 5 4]
其中:
poisson.pmf(k, lambda_): 计算 P(X = k)。
poisson.cdf(k, lambda_): 计算 P(X <= k)。
poisson.sf(k, lambda_): 计算 P(X > k)。
poisson.rvs(lambda_, size=100): 生成100个服从 Pois(λ) 的随机数。
图表会直观地显示泊松分布的形状(总是右偏<右边的尾巴比较长>,但随着λ增大,会逐渐变得对称)。