【散列函数】哈希函数简介

哈希函数简介

[一、散列函数（Hash function)](#一、散列函数（Hash function))
- [1. 散列函数的特点](#1. 散列函数的特点)
- - [1.1 理论上不可逆：](#1.1 理论上不可逆：)
  - [1.2 实际上可穷举：](#1.2 实际上可穷举：)
二、加密和非加密散列函数
- [1. 基本定义](#1. 基本定义)
- [2. 核心区别对比表](#2. 核心区别对比表)
- [3. 应用场景](#3. 应用场景)
[三、散列表（Hash Table）](#三、散列表（Hash Table）)
- [1. 哈希表的基本操作](#1. 哈希表的基本操作)
- [2. 哈希函数在哈希表中的作用](#2. 哈希函数在哈希表中的作用)
- [3. 哈希冲突（Collision）](#3. 哈希冲突（Collision）)
[四、DJB2 字符串哈希算法](#四、DJB2 字符串哈希算法)
- [1. DJB2 hash算法](#1. DJB2 hash算法)

一、散列函数（Hash function)

Hash，一般翻译做散列、或音译为哈希，是把任意长度的输入（又叫做预映射pre-image）通过散列算法变换成固定长度的输出，该输出就是散列值，通常也被叫做哈希值（Hash Value）或消息摘要（Message Digest）。

这种转换是一种压缩映射，散列值的空间通常远小于输入的空间，不同的输入可能会散列成相同的输出，所以不可能从散列值来确定唯一的输入值。简单的说就是一种将任意长度的消息压缩到某一固定长度的哈希值的函数。

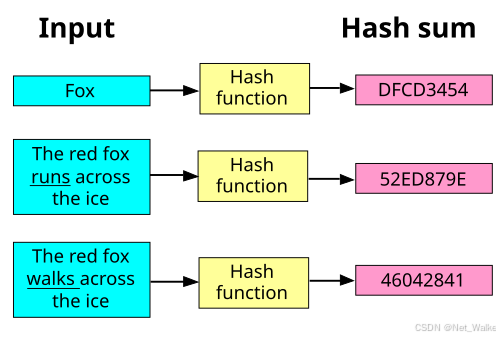
1. 散列函数的特点

特性	说明
固定长度输出	不论输入数据长短，输出的哈希值长度都固定，比如 SHA-256 总是 256 位。
确定性	相同输入一定得到相同输出。
快速计算	计算速度快，适合大量数据处理。
雪崩效应	输入只改一个字节，输出哈希值会完全不同。
均匀分布	输出结果尽量在哈希空间中均匀分布，避免"碰撞"。
单向性	难以从哈希值反推出原始输入（不可逆）。

1.1 理论上不可逆：

哈希函数不是双向函数，它只保留了输入数据的某些数值关系。
哈希函数的输出是固定长度（常见为 32 或 64 位整数），信息量远小于输入。

信息丢失 → 理论上无法精确恢复原始输入。

由于哈希函数的输出是固定长度，信息量远小于输入，这造成原始数据信息丢失，理论上无法通过哈希值精确恢复原始输入。

1.2 实际上可穷举：

以DJB2 哈希算法为例：

DJB2 没有防逆向特性，也就是说，攻击者可以：
- 枚举所有可能输入；
- 对每个输入计算 DJB2 值；
- 与目标哈希值比对；
- 找出可能匹配的输入。

这种方法称为 暴力枚举 / 彩虹表攻击。对小输入范围（例如短字符串）是完全可行的。

二、加密和非加密散列函数

1. 基本定义

类型	定义
加密哈希函数（Cryptographic Hash Function）	专为安全目的设计的哈希函数，具有防篡改、抗碰撞、不可逆等特性。常见于密码学、数字签名、区块链等。
非加密哈希函数（Non‑Cryptographic Hash Function）	主要用于高效数据处理，例如哈希表查找、数据分布、去重等，不追求安全特性。

2. 核心区别对比表

对比维度	🔒 加密哈希函数	⚙️ 非加密哈希函数
设计目标	安全性：抗碰撞、抗逆向、抗篡改	性能：计算快、分布均匀
抗碰撞性	很强（难以找到不同输入产生相同输出）	弱（可能较容易发生碰撞）
单向性（不可逆）	强，几乎无法从输出反推输入	弱，可通过枚举或构造攻击找到输入
雪崩效应	强，极微小变化导致输出完全不同	一般，也会变化但安全性不保证
性能（计算速度）	相对较慢（计算复杂，安全性强）	非常快（结构简单）
输出长度	通常较长（128--512 位），增强安全性	可自定义，一般较短（32--64 位）
典型算法示例	`SHA-256`、`SHA-3`、`BLAKE2`、`MD5`（曾流行）	`DJB2`、`MurmurHash`、`FNV`、`CityHash`
应用场景	密码学、签名、验证完整性、区块链	哈希表、数据索引、负载均衡、去重
是否可被暴力破解	理论上极难、几乎不可能	对小范围输入可轻易穷举

3. 应用场景

不同的应用场景对"安全性"与"速度"的要求不同：

场景	推荐类型	原因
密码存储 / 数字签名	加密哈希函数	确保无法反推或伪造
哈希表 / 分布式存储	非加密哈希函数	追求性能与均匀分布
文件校验、防篡改	加密哈希函数	保证数据未被修改
数据分片 / 去重	非加密哈希函数	快速、轻量化处理

三、散列表（Hash Table）

散列表（Hash Table，也称哈希表） 是一种：

通过"哈希函数",将键（key）映射到一个存储位置（索引），从而以 接近 O(1) 时间完成插入、查找和删除操作的数据结构。

简单理解：

哈希表是一种"先算位置、再存取"的超级高效查找方式。

散列表（哈希表）是一种利用哈希函数把键映射到数组下标，从而实现近似 O(1) 查找的数据结构。

1. 哈希表的基本操作

操作	步骤	时间复杂度（平均）
插入 (Insert)	根据 key 计算哈希值 → 存入对应槽位	O(1)
查找 (Search)	根据 key 计算哈希值 → 直接定位槽位 → 返回值	O(1)
删除 (Delete)	根据 key 定位 → 删除条目	O(1)
碰撞处理	当两个不同 key 哈希到同一槽位时，需额外策略	O(1)~O(n)

2. 哈希函数在哈希表中的作用

哈希函数是哈希表的"心脏" ❤️

一个好的哈希函数应当：

快速可计算；
尽量避免冲突（分布均匀）；
输出结果与 key 变化强相关。

例如：

对字符串：h(s) = (s[0]*31^n + s[1]*31^(n-1) + ... + s[n]) mod table_size
对整数：h(x) = x mod table_size

3. 哈希冲突（Collision）

⚠️ 不可避免的现象：

两个不同的 key 经过哈希函数计算后得到相同的索引。

常见解决方法：

方法	原理	示例
链地址法（Chaining）	每个槽位存一个链表或集合	一个桶里装多个元素
开放定址法（Open Addressing）	冲突时寻找下一个空槽位	线性探测 / 二次探测
再哈希法（Rehashing）	再用不同哈希函数重新计算	避免集中冲突

四、DJB2 字符串哈希算法

DJB2 的主要作用是：

将任意长度的数据（通常是字符串）转换成一个固定长度的整数值，用于快速查找、比较或校验。

djb2以其简单和良好的分布性 而受欢迎，在嵌入式环境中资源紧张，djb2的低计算量和低内存占用是其优势。

常见用途包括：

用途	说明
🔹 哈希表键值计算	用字符串作为 key 的哈希表中，用 DJB2 将字符串映射为整数索引，例如在 symbol table、字典或配置表中。
🔹 字符串快速比较	在需要频繁比较字符串的场景下（例如命令解析、关键字识别），先计算哈希值，可减少逐字节比较次数。

1. DJB2 hash算法

DJB2 实现如下：

c 复制代码

unsigned long djb2(const unsigned char *str)
{
    unsigned long hash = 5381;   // 初始种子
    int c;
    while (c = *str++)
        hash = ((hash << 5) + hash) + c; /* hash * 33 + c */
    return hash;
}

核心思想：

每次乘以 33（通过左移 5 再加原值实现，速度快）；
然后加上当前字符；
最终形成"低碰撞率"的哈希分布。

在字符串快速对比中，使用哈希值比较可以避免逐字节比较，提高效率。如下以一个字符串命令匹配场景来演示字符串哈希算法djb2的使用。

c 复制代码

#include <stdio.h>
#include <stdint.h>
#include <string.h>

uint32_t djb2(const char *str)
{
    uint32_t hash = 5381;   // 初始种子
    int c;
    while (c = *str++){
        hash = ((hash << 5) + hash) + c; /* hash * 33 + c */
    }
    return hash;
}

// 假设我们支持以下命令
typedef enum {
    CMD_LED_ON,
    CMD_LED_OFF,
    CMD_STATUS,
    CMD_UNKNOWN
} cmd_id_t;

typedef struct {
    const char *name;
    uint32_t hash;
    cmd_id_t id;
} cmd_map_t;

static cmd_map_t cmd_table[] = {
        { "LED_ON",  0, CMD_LED_ON },
        { "LED_OFF", 0, CMD_LED_OFF },
        { "STATUS",  0, CMD_STATUS },
};

#define CMD_TABLE_SIZE (sizeof(cmd_table)/sizeof(cmd_map_t))

void init_cmd_hash_table(void)
{
    for (size_t i = 0; i < CMD_TABLE_SIZE; i++) {
        // 在启动时预先计算哈希值
        ((cmd_map_t *)(&cmd_table[i]))->hash = djb2(cmd_table[i].name);
    }
}

cmd_id_t lookup_command(const char *cmd)
{
    uint32_t h = djb2(cmd);
    for (size_t i = 0; i < CMD_TABLE_SIZE; i++) {
        if (cmd_table[i].hash == h) {
            // 为保险，也想做个字符串对比以防哈希碰撞
            if (strcmp(cmd, cmd_table[i].name) == 0) {
                return cmd_table[i].id;
            }
        }
    }
    return CMD_UNKNOWN;
}

void handle_command(const char *cmd)
{
    cmd_id_t id = lookup_command(cmd);
    switch (id) {
        case CMD_LED_ON:  printf("Turn LED on\n"); break;
        case CMD_LED_OFF: printf("Turn LED off\n"); break;
        case CMD_STATUS:  printf("Status OK\n"); break;
        default:          printf("Unknown cmd: %s\n", cmd); break;
    }
}

int main(void)
{
    printf("djb2 hash demo\n");
    init_cmd_hash_table();
    handle_command("LED_ON");
    handle_command("STATUS");
    handle_command("FOO");
    return 0;
}

输出结果：

c 复制代码

djb2 hash demo
Turn LED on
Status OK
Unknown cmd: FOO