【LeetCode】四数之和

文章目录

前言
题目描述
算法原理
代码实现

前言

道友们，今天咱们来做四数之和！

题目描述

给你一个由 n 个整数组成的数组 nums ，和一个目标值 target 。请你找出并返回满足下述全部条件且不重复 的四元组[nums[a], nums[b], nums[c], nums[d]] （若两个四元组元素一一对应，则认为两个四元组重复）：

0 <= a, b, c, d < n

a、b、c 和 d 互不相同

nums $a$ + nums $b$ + nums $c$ + nums $d$ == target

你可以按 任意顺序 返回答案。
示例 1：

输入： nums = $1,0,-1,0,-2,2$ , target = 0
输出： $\[-2,-1,1,2$ , $-2,0,0,2$ , $-1,0,0,1$ ]
示例 2：

输入： nums = $2,2,2,2,2$ , target = 8
输出： $\[2,2,2,2$ ]
提示：

1 <= nums.length <= 200
-10^9 <= nums[i] <= 10^9
-10^9 <= target <=10^9

算法原理

这道题跟我们做的上一道题很类似，只不过要更复杂一点，但是做法是相同的。

首先我们对数组排序，方便我们后续去重和使用双指针算法，以示例 1 为例：

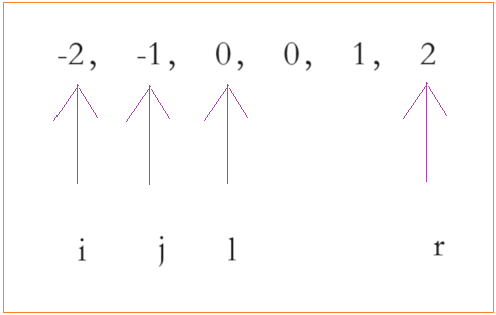
排完序之后，固定最左边的元素，在它的右区间找三个数，使这三个数的和与我们固定的数再相加结果为 target，我们可以看到，在右区间找三个数的过程就是我们上次做的那道三数之和的问题，如果没看过的道友可以去看一下。

这里去重操作我们依然有两种写法，即用 set 去重、自己手动去重，这道题的代码逻辑和三数之和几乎一模一样，包括在越界等细节方面的处理，如果三数之和那道题会做了，那这道题是很简单的。

总体上，四数之和这道题就是在三数之和的基础上多套了一层！

代码实现

用set去重

cpp 复制代码

class Solution 
{
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) 
    {
        int n = nums.size();
        sort(nums.begin(), nums.end());
        set<vector<int>> s;

        for (int i = 0; i < n - 3; ++i)
        {
            for (int j = i + 1; j < n - 2; ++j)
            {
                long long int tag = (long long)target - nums[i] - nums[j];
                int left = j + 1, right = n - 1;
                while (left < right)
                {
                    if (nums[left] + nums[right] < tag)
                    {
                        left++;
                    }
                    else if(nums[left] + nums[right] > tag)
                    {
                        right--;
                    }
                    else
                    {
                        s.insert({nums[i], nums[j], nums[left], nums[right]});
                        left++;
                        right--;
                    }
                }
            }
        }
        vector<vector<int>> v;
        for (auto& e : s)
        {
            v.push_back(e);
        }
        return v;
    }
};

自己手动去重

cpp 复制代码

class Solution 
{
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) 
    {
        int n = nums.size();
        sort(nums.begin(), nums.end());
        vector<vector<int>> v;

        for (int i = 0; i < n - 3;)
        {
            for (int j = i + 1; j < n - 2;)
            {
                long long int tag = (long long int)target - nums[i] - nums[j];
                int left = j + 1, right = n - 1;
                while (left < right)
                {
                    if (nums[left] + nums[right] < tag)
                    {
                        left++;
                    }
                    else if(nums[left] + nums[right] > tag)
                    {
                        right--;
                    }
                    else
                    {
                        v.push_back({nums[i], nums[j], nums[left], nums[right]});
                        left++;
                        right--;
                        while(left < right && nums[left] == nums[left - 1]) left++;
                        while(left < right && nums[right] == nums[right + 1]) right--;
                    }
                }
                ++j;
                while(j < n - 2 && nums[j] == nums[j - 1]) ++j;
            }
            ++i;
            while(i < n - 3 && nums[i] == nums[i - 1]) ++i;
        }
        return v;
    }
};

这里有一个要注意的点，我们在一个区间找目标值的时候要先计算出我们要找的目标值，如果我们把目标值的类型定义为 int 的话，在一些用例中是会越界的，这里我们可以用 long long来存一下。

cpp 复制代码

long long int tag = (long long int)target - nums[i] - nums[j];

要注意左边的变量也要强转一下，三个变量里面强转任意一个都行，因为剩下的两个会发生算数转换。

完！