1.题目

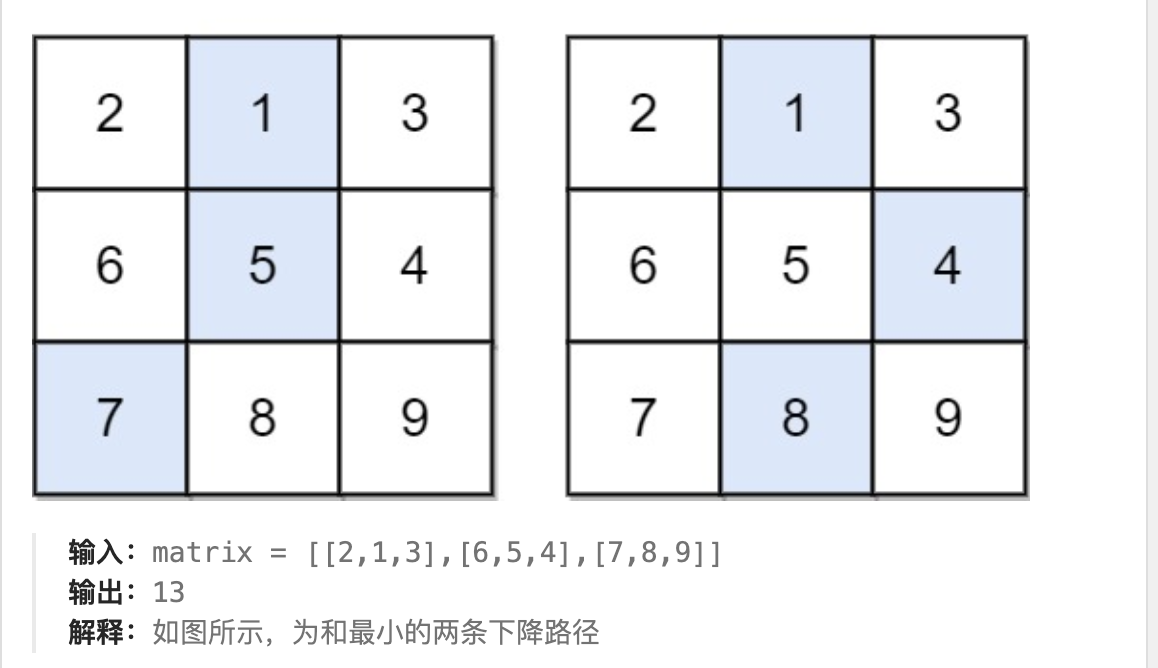

2.思路
因为这题的转移方向是"从上到下"(上一行的 j−1、j、j+1 到下一行 j),所以唯一需要的基线就是第一行:
dp[0][j] = matrix[0][j]。
之后第 i 行的任意列 j 都只依赖 上一行 的值(dp[i-1][*]),自然能算出来,包括第 0 列:
当 j == 0:dp[i][0] 由 dp[i-1][0](正上)和(若存在)dp[i-1][1](右上)转移得到。
当 0 < j < n-1:取 dp[i-1][j-1], dp[i-1][j], dp[i-1][j+1] 的最小。
当 j == n-1:由 dp[i-1][n-1](正上)和(若存在)dp[i-1][n-2](左上)转移。
也就是说,第一列不是独立的"起点边界",它和其他列一样,都依赖"上一行"的结果,自然会被计算到;不需要像"从左到右/从上到下"的网格最短路(只能向右或向下)那样同时初始化第一行和第一列。
java
dp[0][0] = matrix[0][0] // 初始化第一行
dp[1][0] = min(dp[0][0], dp[0][1]) + matrix[1][0]
dp[2][0] = min(dp[1][0], dp[1][1]) + matrix[2][0]约定是 dp[i][j]:i 是行(row),j 是列(column)。
dp[0] 在 Java 里表示第一行这一整行的一维数组;所以写成 dp[0] = [2, 1, 3] 就是说第一行的每一列值依次是 2、1、3,也就是 (0,0)、(0,1)、(0,2)。
java
dp[0][0] dp[0][1] dp[0][2] ← 这是第0行
dp[1][0] dp[1][1] dp[1][2]
dp[2][0] dp[2][1] dp[2][2]
↑ 第0列3.代码实现
java
class Solution {
public int minFallingPathSum(int[][] matrix) {
//行数
int m=matrix.length;
//列数
int n=matrix[0].length;
int[][] dp=new int[m][n];
// "从上到下",所以从第一行中的任何元素开始。初始化第一行:到达第一行的最小路径和就是其自身
// 即 (0,0),(0,1),(0,2),代表矩阵数组中的第一组元素
for(int j=0;j<n;j++)
{
dp[0][j]=matrix[0][j];
}
for(int i=1;i<m;i++)
{
for(int j=0;j<n;j++)
{
//最左边的元素
if(j==0)
{
dp[i][j]=Math.min(dp[i-1][j],dp[i-1][j+1])+matrix[i][j];
}
//最右边的元素
else if(j==n-1)
{
dp[i][j]=Math.min(dp[i-1][j],dp[i-1][j-1])+matrix[i][j];
}
//中间正常元素
else
{
dp[i][j]=Math.min(Math.min(dp[i-1][j-1],dp[i-1][j]),dp[i-1][j+1])+matrix[i][j];
}
}
}
int res=dp[m-1][0];//最后一行的第一个元素
//找出最后一行的最小值
for(int k=0;k<n;k++)
{
res=Math.min(res,dp[m-1][k]);
}
return res;
}
}