MATLAB基于GWO-BP神经网络对某拨叉件锻造金属流动性的参数分析

---

🎯 一、问题定义与研究目标

核心问题：

建立拨叉件锻造过程中工艺参数与金属流动性的映射关系模型

具体目标：

1. 参数敏感性分析：识别影响金属流动性的关键工艺参数
2. 流动性预测：建立工艺参数→流动性的高精度预测模型
3. 工艺优化：寻找最优工艺参数组合以提高成形质量

---

🔧 二、技术路线架构

工艺参数采集 → 数据预处理 → GWO优化BP网络 → 模型训练 → 参数分析 → 工艺优化
     ↓              ↓           ↓          ↓         ↓         ↓
  温度/速度/   归一化/特征  灰狼算法优化  神经网络  敏感性分析  最优参数
  摩擦系数等    选择     网络初始权重  训练预测  贡献度计算  推荐

---

🧮 三、算法步骤详解

阶段1：数据准备与预处理

1. 参数确定：

   • 锻造温度（800-1200°C）
   • 变形速度（0.1-10 mm/s）
   • 摩擦系数（0.1-0.3）
   • 模具几何参数
   • 材料初始状态参数

2. 数据采集：

   • 实验数据 + 有限元仿真数据
   • 样本数量：N ≥ 200
   • 输出指标：流动距离、填充率、应变分布均匀性

3. 数据预处理：

   % 数据归一化
   [input_normalized, input_ps] = mapminmax(input_data, 0, 1);
   [output_normalized, output_ps] = mapminmax(output_data, 0, 1);

阶段2：GWO-BP神经网络构建

2.1 BP神经网络结构

% 网络参数
input_size = 6;     % 输入参数个数
hidden_size = 12;   % 隐含层神经元数
output_size = 3;    % 输出指标数

% 网络创建
net = newff(input_normalized, output_normalized, hidden_size, {
    'tansig', 'purelin'}, 'trainlm');

2.2 GWO优化算法

灰狼优化算法原理：

• α狼：当前最优解
• β狼：次优解
• δ狼：第三优解
• ω狼：其他候选解

位置更新公式：

% 包围猎物
D_alpha = abs(C1 .* X_alpha - X);
D_beta  = abs(C2 .* X_beta - X);
D_delta = abs(C3 .* X_delta - X);

X1 = X_alpha - A1 .* D_alpha;
X2 = X_beta - A2 .* D_beta; 
X3 = X_delta - A3 .* D_delta;

X_new = (X1 + X2 + X3) / 3;

2.3 GWO优化BP流程

% GWO参数设置
wolf_num = 30;      % 灰狼数量
max_iter = 100;     % 最大迭代次数
dim = input_size * hidden_size + hidden_size * output_size + hidden_size + output_size;

for iter = 1:max_iter
    % 1. 计算适应度（网络训练误差）
    for i = 1:wolf_num
        % 将灰狼位置解码为网络权重
        [W1, B1, W2, B2] = decode_position(positions(i,:), input_size, hidden_size, output_size);
        
        % 设置网络权重
        net.IW{1,1} = W1; net.LW{2,1} = W2;
        net.b{1} = B1; net.b{2} = B2;
        
        % 计算适应度
        fitness(i) = calculate_fitness(net, train_data, train_target);
    end
    
    % 2. 更新α、β、δ狼
    [~, sorted_idx] = sort(fitness);
    X_alpha = positions(sorted_idx(1), :);
    X_beta  = positions(sorted_idx(2), :);
    X_delta = positions(sorted_idx(3), :);
    
    % 3. 更新灰狼位置
    a = 2 - iter * (2 / max_iter);  % 收敛因子
    for i = 1:wolf_num
        % 计算A、C系数
        A1 = 2 * a * rand() - a; C1 = 2 * rand();
        A2 = 2 * a * rand() - a; C2 = 2 * rand(); 
        A3 = 2 * a * rand() - a; C3 = 2 * rand();
        
        % 位置更新
        D_alpha = abs(C1 .* X_alpha - positions(i,:));
        D_beta  = abs(C2 .* X_beta - positions(i,:));
        D_delta = abs(C3 .* X_delta - positions(i,:));
        
        X1 = X_alpha - A1 .* D_alpha;
        X2 = X_beta - A2 .* D_beta;
        X3 = X_delta - A3 .* D_delta;
        
        positions(i,:) = (X1 + X2 + X3) / 3;
    end
end

阶段3：参数敏感性分析

3.1 基于权重的贡献度分析

% 计算输入参数对输出的贡献度
for i = 1:input_size
    contribution(i) = sum(abs(net.IW{1,1}(:,i))) / sum(sum(abs(net.IW{1,1})));
end

3.2 基于扰动的敏感性分析

% 单参数扰动分析
base_output = net(normalized_input);
sensitivity = zeros(input_size, 1);

for i = 1:input_size
    perturbed_input = normalized_input;
    perturbed_input(i,:) = perturbed_input(i,:) * 1.1;  % 参数增加10%
    
    perturbed_output = net(perturbed_input);
    sensitivity(i) = mean(abs(perturbed_output - base_output) ./ base_output);
end

---

📊 四、关键技术参数设定

GWO算法参数：

参数	推荐值	说明
灰狼数量	20-50	种群规模
最大迭代次数	100-200	优化代数
收敛因子a	2→0	线性递减
搜索空间	[-1,1]	权重初始化范围

BP网络参数：

参数	推荐值	说明
隐含层数	1-2层	根据问题复杂度
隐含层节点	8-15个	输入节点的1.5-2倍
激活函数	tansig + purelin	非线性映射
训练算法	trainlm	Levenberg-Marquardt

工艺参数范围：

参数	典型范围	单位
锻造温度	800-1200	°C
变形速度	0.1-10	mm/s
摩擦系数	0.1-0.3	无量纲
模具圆角	5-20	mm
拔模斜度	1-5	°

---

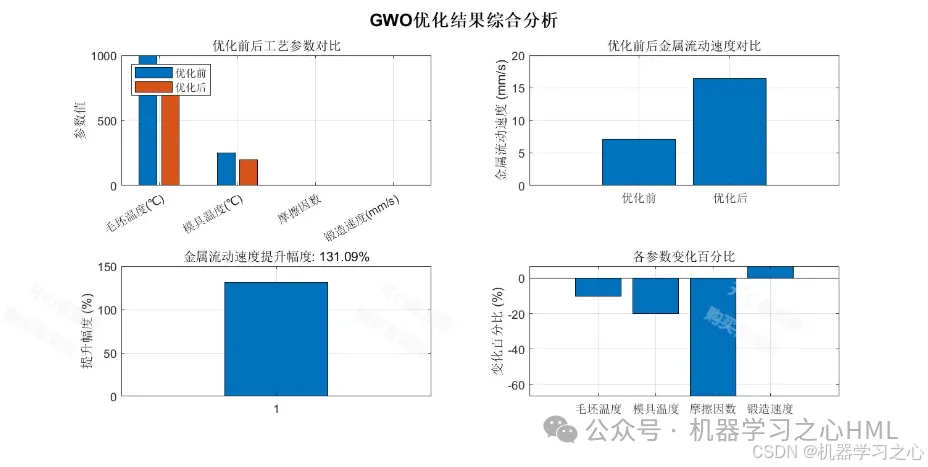
🎨 五、可视化分析方案

1. 优化过程可视化

figure;
plot(1:max_iter, convergence_curve, 'LineWidth', 2);
xlabel('迭代次数'); ylabel('适应度值');
title('GWO算法收敛曲线');
grid on;

2. 参数贡献度可视化

figure;
bar(contribution * 100);
xlabel('工艺参数'); ylabel('贡献度(%)');
title('工艺参数对金属流动性的贡献度分析');
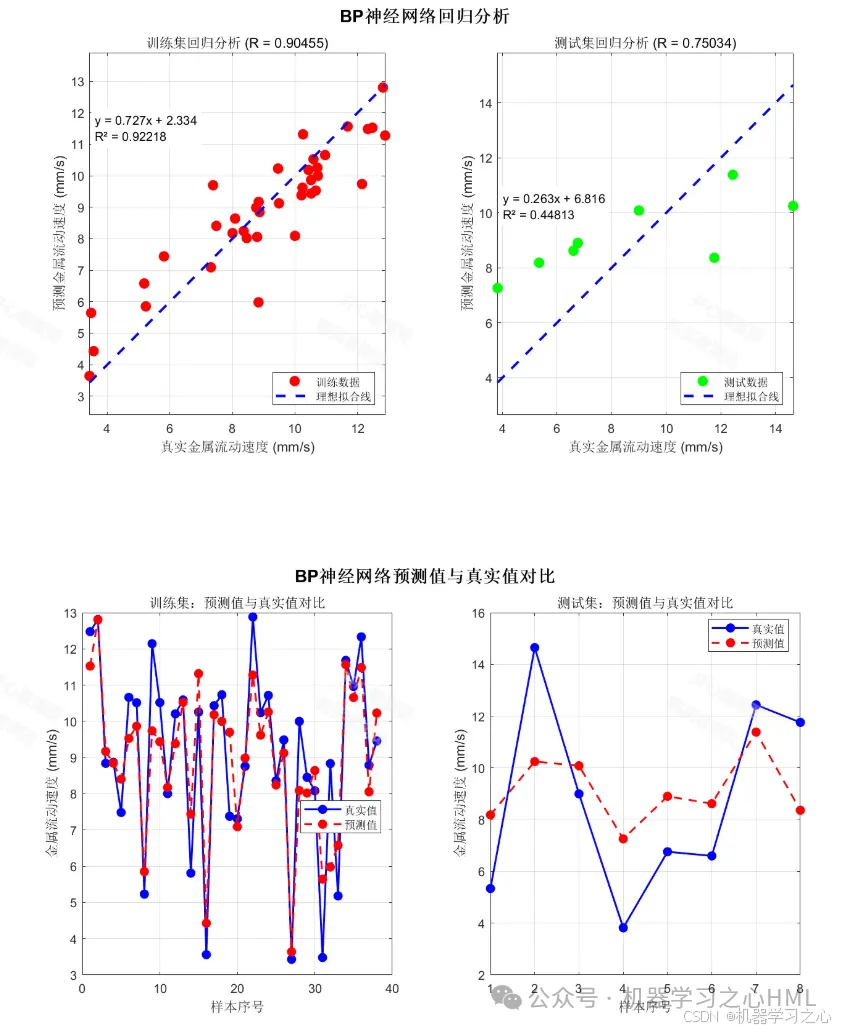
set(gca, 'XTickLabel', param_names);

3. 预测效果可视化

figure;
subplot(2,2,1);
plot(train_target(1,:), train_predict(1,:), 'ro');
hold on; plot([min,max], [min,max], 'k--');
xlabel('实际值'); ylabel('预测值');
title('训练集预测效果');

---

💻 六、运行环境要求

软件环境：

• MATLAB R2018a+
• 必要工具箱 ：
  • Deep Learning Toolbox
  • Optimization Toolbox（可选）
  • Statistics and Machine Learning Toolbox

硬件要求：

• 内存：≥8GB（用于存储仿真数据）
• 处理器：多核CPU推荐
• 存储空间：≥10GB（用于数据存储）

数据文件：

• 工艺参数数据库（Excel/CSV格式）
• 有限元仿真结果文件
• 实验测量数据

---

📈 七、预期成果与应用价值

理论价值：

1. 建立工艺参数-流动性的精确映射模型
2. 揭示多参数耦合作用机制
3. 发展智能材料成形优化方法

工程应用：

1. 工艺参数优化推荐
2. 缺陷预测与预防
3. 模具设计指导
4. 生产质量控制

经济效益：

• 减少试模次数：降低开发成本
• 提高产品质量：减少废品率
• 缩短研发周期：加速产品上市

---

🔍 八、验证与评估方案

模型验证：

1. 交叉验证：k-fold交叉验证评估泛化能力
2. 对比实验：与传统BP、RBF网络对比
3. 物理验证：与有限元仿真结果对比

性能指标：

• 预测精度：R² > 0.95，RMSE < 5%
• 收敛速度：GWO比传统方法快30-50%
• 稳定性：多次运行结果标准差 < 2%

---

这个技术方案为拨叉件锻造过程的金属流动性分析提供了从数据到决策的完整智能化解决方案，将显著提升锻造工艺的设计效率和质量控制水平。

完整代码私信回复MATLAB基于GWO-BP神经网络对某拨叉件锻造金属流动性的参数分析