数据结构基石：单链表的全面实现、操作详解与顺序表对比

时间醉酒2025-10-18 8:02

引言：

上期我们结合代码深入理解了顺序表的功能，这一期我们来探讨一下链式存储结构。在此之前我们来对比一下两个不同的实现线性表这个抽象概念的两种具体结构。

特性 链表 (Linked List) 顺序表 (Sequential List) 链表的优势体现
内存分配 动态，分散存储，按需分配 静态或需预先分配，要求连续存储 灵活性高，无需担心溢出或扩容
中间/头部插入/删除 O(1) （找到位置后） O(n)（需移动后续元素） 高效率
随机访问（按索引查找） O(n)（需从头遍历） O(1)（通过地址计算，直接访问） 劣势
空间开销 高（需要额外的指针域存储地址） 低（只存储数据本身） 劣势

进入正题

1.3 链表

链表是一种基础而重要的数据结构，其核心特点在于：用于存储数据元素的物理空间可以是任意、非连续的。

1. 从顺序表到链表

  • 顺序表的局限：顺序表（如数组）要求占用一片连续的内存空间。这就像电影院排队入场，若想与家人邻座，就必须找到一整排连续的空位。当数据量很大时，寻找连续空间往往变得困难。

  • 链表的优势：链表则更像一场自由入座的讲座。每位参与者（数据元素）可随意寻找空位就座，只需记住同伴（直接后继元素）的座位位置即可。这些座位无需相邻，从而实现了内存的灵活利用。

2. 节点的定义与结构

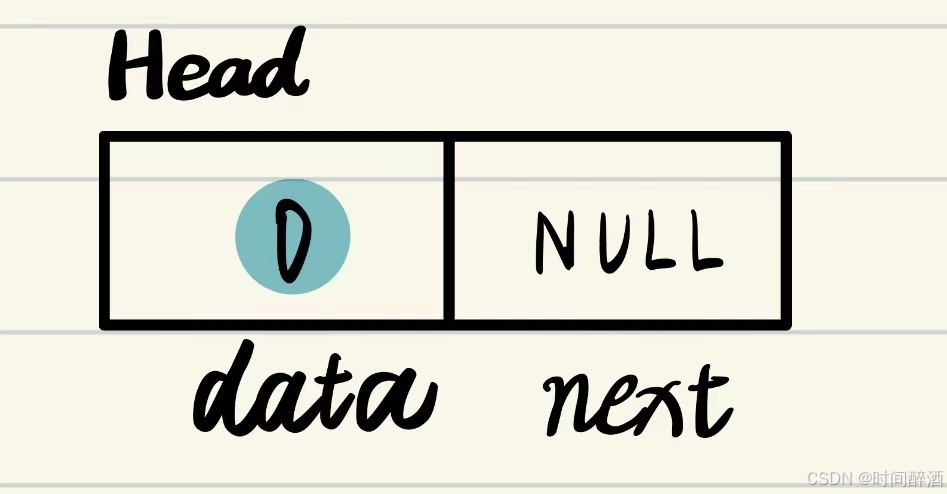
为了在非连续的存储单元中维护数据之间的逻辑关系，每个数据元素除了自身信息外，还需存储其直接后继的位置信息。这两部分共同构成一个节点（Node），即数据元素的存储映像。

每个节点包含两个域：

  • 数据域：存储数据元素本身的信息。

  • 指针域：存储指向直接后继元素所在位置的指针（也称链）。

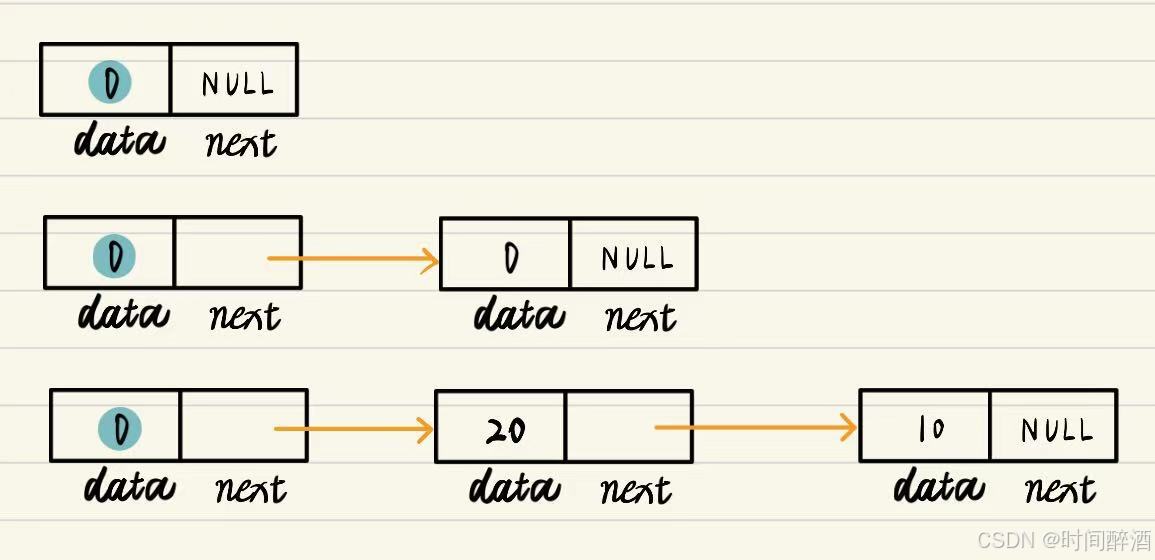
3. 链表的形成

通过指针链接，n 个节点 ( 1 ≤ i ≤ n )可以按逻辑顺序串联起来，形成一个链表，表示线性表 （ ，，，）。尽管节点在内存中可能分散存储，但通过指针的引导，仍能保持逻辑上的连续性。

链表的代码实现：

cs 复制代码 
typedef int ElemType;

typedef struct node{
    ElemType data;
    struct node *next; //指向下一个节点的指针
}Node;

单链表 - 初始化

cs 复制代码 
Node* initList()
{
    Node *head = (Node*)malloc(sizeof(Node));
    head->data = 0;
    head->next = NULL;
    return head;
}

int main()
{
    Node *list = initList();
    return 1;
}

插入数据：头插法，尾插法

头插法： 在头节点后面插入数据

代码实现：

cs 复制代码 
//单链表头插法核心逻辑
int insertHead(Node* L,ElemType e) //传入头指针和插入的元素
{
    Node* p = (Node*) malloc(sizeof(Node)); //相当于在堆内存中创建了一个新的节点
    p->data = e;
    p->next = L->next;
    L->next = p;
}
int main()
{
    Node* list = initList();
    insertHead(list, 20);
    insertHead(list, 10);
    insertHead(list, 50);
    insertHead(list, 70);
    insertHead(list, 90);
    listNode(list);
    return 0;
}

代码解析：

1. Node *p = (Node*)maclloc(sizeof(Node));

  • 功能： 内存动态分配。
  • 解释： 尝试在堆内存中为 一个新的节点 分配足够存储一个 Node 结构体大小的内存空间。
  • 结果： 分配成功后返回该新内存块的地址，赋值给指针 p。p 现在指向新创建的、未初始化的节点。

2. p->data = e;

  • 功能： 数据赋值。
  • 解释： 将传入的元素值 e 存储到新节点 p 的 data 字段中。

3. p->next = L->next;

  • 功能： 链接新节点到旧链的头部。
  • 解释： 这是插入的关键一步。
    • L->next 指向的是 原链表的第一个数据节点 （ L 是头结点）。
    • 这一步操作让新节点 p 的 next 指针 指向了 原链表的第一个数据节点。这样，新节点就成功连接到了旧链表的其余部分。

4. L->next = p;

  • 功能： 更新头指针的指向。
  • 解释： 这一步是完成插入的最后一步。
    • 它将链表的头指针 L 的 next 字段 指向新创建的节点 p。
    • 执行完毕后，新节点 p 就成为了链表的第一个节点。

图解如下：

  1. p->next = L->next;
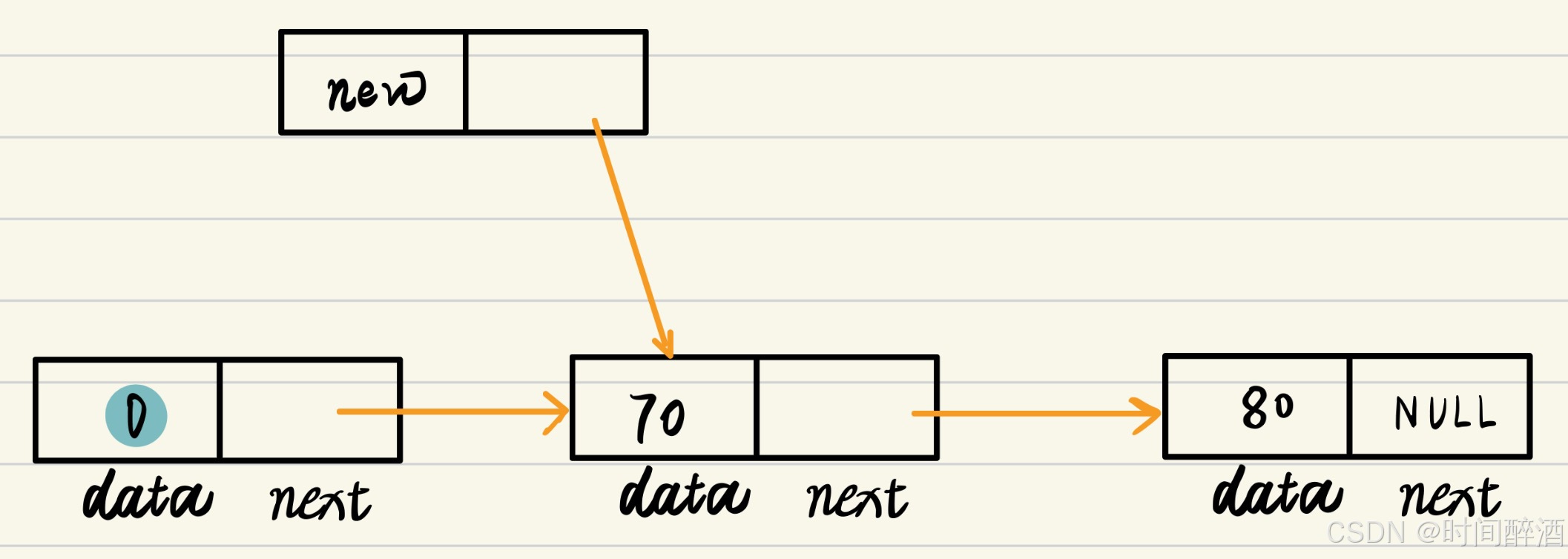
  1. L->next = p;

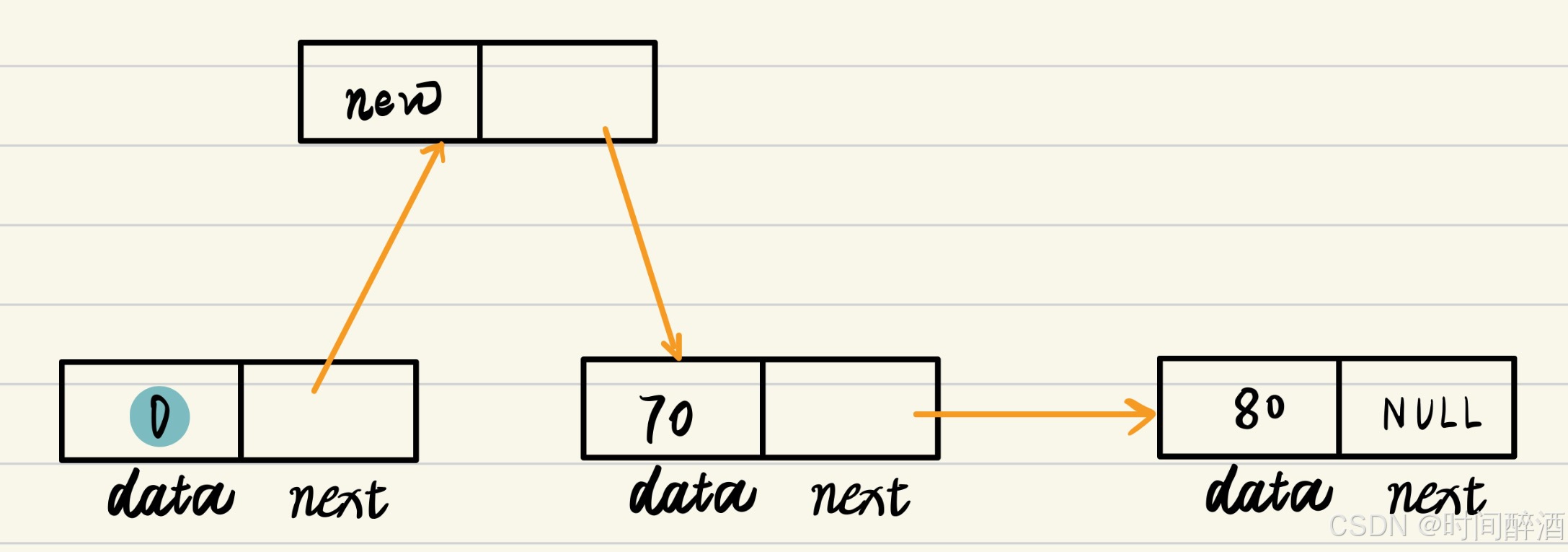
单链表 - 遍历

cs 复制代码 
//遍历函数
void listNode(Node* L)
{
    Node* p = L->next;
    while (p != NULL)
    {
        printf("%d ", p->data);
        p = p->next;
    }
}

在main中调用

cs 复制代码 
int main(int argc,char const *argv[])
{
    Node *list = initList();
    insertHead(list,20);
    insertHead(list,10);
    insertHead(list,50);
    insertHead(list,70);
    insertHead(list,90);
    listNode(list);
    return 0;
}

结果如下：

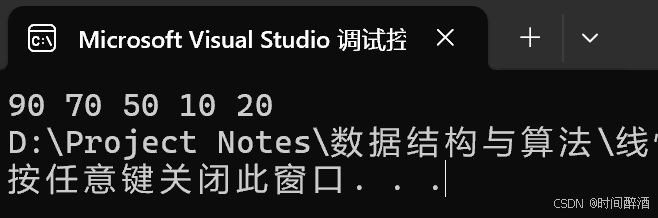
注意：头插法的顺序和排列的顺序是相反的(先进后出)

单链表 - 尾插法

代码实现：

获取尾节点地址

cs 复制代码 
Node* get_tail(Node* L)
{
    Node* p = L;
    while(p->nect != NULL)
    {
        p = p->next;
    }
    return p; //返回尾节点
}

尾插法核心逻辑

cs 复制代码 
//单链表尾差法核心逻辑
Node* insertTail(Node *tail,ElemType e) //传入尾节点和要插入的数值
{
    Node *p = (Node*)malloc(sizeof(Node));
    p->data = e;
    tail->next = p;
    p->next = NULL;
    return p; //插入的数据成为新的尾节点
}

在main中调用

cs 复制代码 
int main(int argc,char const* argv[])
{
    Node* list = initList();
    Node* tail = get_tail(list);
    tail = insertTail(tail,10);
    tail = insertTail(tail,20);
    tail = insertTail(tail,30);
    listNode(list);
    return 0;
}

结果如下：

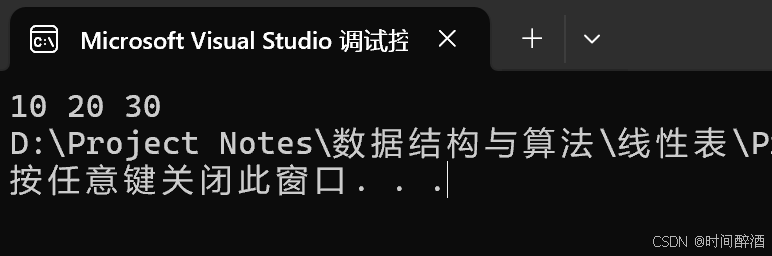
单链表 - 在指定位置插入数据

cs 复制代码 
//在单链表中指定位置插入数据
int insertNode(Node* L,int pos,ElemType e)
{
    //保存插入位置的前驱节点
    Node* p = L;
    int i = 0;
    //遍历链表找到插入位置的前驱节点
    while(i < pos-1)
    {
        p = p->next;
        i++;
        if(p == NULL)
        {
            return 0;
        }
    }
    //要插入的新节点
    Node* q = (Node*)malloc(sizeof(Node));
    q->data = e;
    q->next = p->next;
    p->next = q;
    return 1;
}

在mian中调用

cs 复制代码 
int main(int argc,char const* argv[])
{
    insertNode(list,2,15);
    listNode(list);
    retrun 0;
}

结果如下：

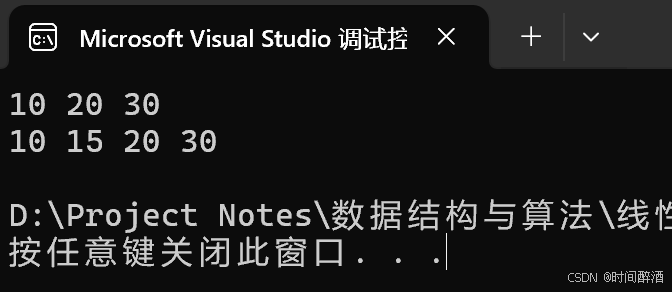
单链表 - 删除节点

步骤总结:

找到要删除节点的前置节点p

用指针q记录要删除的节点

通过改变p的后继节点实现删除

释放删除节点的空间

图文解释：

cs 复制代码 
//删除节点
int deleteNode(Node* L,int pos)
{
    //要删除节点的前驱
    Node* p = L: 
    int i = 0;
    //遍历链表，找到要删除的节点的前驱
    while(i < pos-1)
    {
        p = p->next;
        i++;
        if(p == NULL)
        {
            return 0;
        }
    }

    if(p->next == NULL)
    {    
        printf("删除的位置错误");
        return 0;
    }
   //q指向要删除的节点
     Node* q = p->next;
   //让要删除的节点的前驱指向要删除节点的后继
     p->next = q->next;
   //释放被删除节点的内存空间
     free(q);

     return 1;
}

单链表 - 获取链表长度

cs 复制代码 
int listLength(Node* L)
{
    Node* p = L;
    int len = 0;
    while(p != NULL)
    {
        p = p -> next;
        len++;
    }
    return len;
}

单链表 - 释放链表

步骤总结：

指针p指向头节点后的第一个节点

判断指针p是否指向空姐点

如果p不为空，用指针q记录p的后继节点

释放指针p指向的节点

指针p和指针p指向同一个节点，循环上面的操作

代码的实现：

cs 复制代码 
//释放链表
void freeList(Node* L)
{
    Node *p = L->next;
    Node *q;
        
    while(p != NULL)
    {
        q = p->next;
        free(p);
        p = q;
    }
    L->next = NULL;
}

在main中的实现

cs 复制代码 
int main(int argc,char const* argv[])
{
printf("%d\n", listLength(list));
freeList(list);
printf("%d\n", listLength(list));
}

结果如下：

完整代码如下：

cs 复制代码 
#include <stdio.h>
#include <stdlib.h>

typedef int ElemType;

//结构体定义（Node）
typedef struct node {
    ElemType data;
    struct node* next; //指向下一个节点的指针
}Node;

//单链表初始化函数（Node）
 Node* initList()
{
    Node* head = (Node*)malloc(sizeof(Node));
    head->data = 0;
    head->next = NULL;
    return head;
}

//单链表头插法核心逻辑
int insertHead(Node* L, ElemType e) //传入头指针和插入的元素
{
    Node* p = (Node*)malloc(sizeof(Node)); //相当于在堆内存中创建了一个新的节点
    p->data = e;
    p->next = L->next;
    L->next = p;

    return 0;
}
Node* get_tail(Node* L)
{
    Node* p = L;
    while (p->next != NULL)
    {
        p = p->next;
    }
    return p;
}
//单链表尾插法核心逻辑
Node* insertTail(Node* tail, ElemType e)
{
    Node* p = (Node*)malloc(sizeof(Node));
    p->data = e;
    tail->next = p;
    p->next = NULL;
    return p;
}
//单链表指定位置插入元素核心逻辑
int insertNode(Node* L, int pos, ElemType e)
{
    //保存插入位置的前驱节点
    Node* p = L;
    int i = 0;
    //遍历链表找到插入位置的前驱节点
    while (i < pos - 1)
    {
        p = p->next;
        i++;
        if (p == NULL)
        {
            return 0;
        }
    }
    //要插入的新节点
    Node* q = (Node*)malloc(sizeof(Node));
    q->data = e;
    q->next = p->next;
    p->next = q;
    return 1;
}
//删除节点核心逻辑
int deleteNode(Node* L, int pos)
{
    //要删除节点的前驱
    Node* p = L;
    int i = 0;
    //遍历链表，找到要删除的节点的前驱
    while (i < pos - 1)
    {
        p = p->next;
        i++;
        if (p == NULL)
        {
            return 0;
        }
    }

    if (p->next == NULL)
    {
        printf("删除的位置错误\n");
        return 0;
    }

    //q指向要删除的节点
    Node* q = p->next;
    //让要删除的节点的前驱指向要删除节点的后继
    p->next = q->next;
    //释放被删除节点的内存空间
    free(q);

    return 1;
}
//获取链表长度
int listLength(Node* L)
{
    Node* p = L;
    int len = 0;
    while (p != NULL)
    {
        p = p->next;
        len++;
    }
    return len;
}
//释放链表
void freeList(Node* L)
{
    Node* p = L->next;
    Node* q;

    while (p != NULL)
    {
        q = p->next;
        free(p);
        p = q;
    }
    L->next = NULL;
}


//遍历函数
void listNode(Node* L)
{
    Node* p = L->next;
    while (p != NULL)
    {
        printf("%d ", p->data);
        p = p->next;
    }
    printf("\n");
}
int main(int argc, char const* argv[])
{
    Node* list = initList();
    insertHead(list, 20);
    insertHead(list, 10);
    insertHead(list, 50);
    insertHead(list, 70);
    insertHead(list, 90);
    listNode(list);

    Node* list = initList();
    Node* tail = get_tail(list);
    tail = insertTail(tail, 10);
    tail = insertTail(tail, 20);
    tail = insertTail(tail, 30);
    listNode(list);
    insertNode(list, 2, 15);
    listNode(list);

    deleteNode(list, 2);
    listNode(list);

    printf("%d\n", listLength(list));
    freeList(list);
    printf("%d\n", listLength(list));
    return 0;
}

总结：

通过本期的学习，我们深入探讨了链式存储结构------链表的核心原理与实现方式。从节点的定义、链表的形成，到头插法、尾插法、指定位置插入和删除节点等基本操作，我们一步步构建了对链表的完整认知。

与上期学习的顺序表相比，链表在动态内存分配和插入删除效率方面展现出明显优势，特别是在需要频繁进行结构调整的场景下。虽然链表在随机访问方面不如顺序表高效，但其灵活的内存使用方式使其在实际应用中具有不可替代的价值。

理解链表不仅有助于我们掌握基础的数据结构知识，更重要的是为我们后续学习更复杂的链式结构（如双向链表、循环链表等）打下了坚实基础。数据结构的选择往往需要在时间与空间效率之间进行权衡，而链表正是这种权衡思维的最佳体现之一。

相关推荐
Miraitowa_cheems15 小时前
LeetCode算法日记 - Day 73: 最小路径和、地下城游戏
数据结构·算法·leetcode·职场和发展·深度优先·动态规划·推荐算法
野蛮人6号15 小时前
力扣热题100道之560和位K的子数组
数据结构·算法·leetcode
小白不想白a17 小时前
每日手撕算法--哈希映射/链表存储数求和
数据结构·算法
Doro再努力18 小时前
数据结构04：力扣顺序表3道例题解题思路与代码实现
c语言·数据结构
HY小海18 小时前
【C++】AVL树实现
开发语言·数据结构·c++
花月C18 小时前
高效查找数据的数据结构—MySQL 索引
数据结构·数据库·mysql
仰泳的熊猫18 小时前
LeetCode:701. 二叉搜索树中的插入操作
数据结构·c++·算法·leetcode
小L～～～1 天前
2025吉比特-游戏引擎开发-一面复盘
数据结构·算法·游戏引擎
potato_may1 天前
第18讲：C语言内存函数
c语言·数据结构·算法
热门推荐
01BongoCat - 跨平台键盘猫动画工具02GitHub 镜像站点03两千字总结：Codex 国内如何安装和使用的教程，以及如何设置中文回答04UV安装并设置国内源05Linux下V2Ray安装配置指南06GitLab 零基础入门指南：从安装到项目管理全流程07windows找不到gpedit.msc（本地组策略编辑器）0846个Nano-banana 精选提示词，持续更新中09在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）10KGG转MP3工具|非KGM文件|解密音频