单序列和双序列问题——动态规划

文章目录

一、最长递增子序列
二、等差数列划分II-子序列
三、最长公共子序列
四、正则表达式匹配

动态规划是解决复杂算法问题的利器，本文将聚焦于单序列与双序列两类经典问题，通过分析最长递增子序列、正则表达式匹配等典型案例，深入剖析动态规划的状态定义与转移方程构建思路。

在阅读该文章时最好对基础的动态规划有所了解，因为在此不会讲解动态规划基础的细节，大家可以通过阅读下文进行学习：

基础dp------动态规划

多状态dp------动态规划

子数组问题------动态规划

单序列问题往往具备两个关键特征，使其特别适合用动态规划求解。

问题解决路径需拆解为多个步骤，每个步骤都存在多种选择，最终目标是计算可行解的总数，或是找到满足条件的最优解。
问题的输入数据通常呈现为序列形态，比如一维数组、字符串等典型的线性数据结构。

根据题目的特点找出该元素对应的最优解（或解的数目）和前面若干元素（通常是一个或两个）的最优解（或解的数目）的关系，并以此找出相应的状态转移方程。一旦找出了状态转移方程，只要注意避免不必要的重复计算，问题就能迎刃而解。

下面讲解两个适合运用动态规划的单序列问题

一、最长递增子序列

这是一个非常经典的题目，该题本身比较简单，而且非常有借鉴性，可以作为模版题，很多题的解题思路可以照搬这道题。

题目解析：

作为动态规划领域的 "入门标杆题"，最长递增子序列（LIS）不仅是面试高频考点，更是后续复杂子序列问题（如最长递增子序列的个数、二维 LIS 等）的基础模型。其核心是理解 "子序列的非连续性" 与 "递增的严格性"，并通过动态规划将暴力枚举的高复杂度优化到可接受范围。

区分子数组（子串）与子序列：

子数组（子串）：在数列中的一段连续的元素组成的新数列，中间不可间断。
子序列：在数列中从左往右依次挑选出元素组成的新数列，或者说在数列中随意删除一些元素后，剩下的元素组成的新数列。（子序列的元素间相对位置与原数组相同）

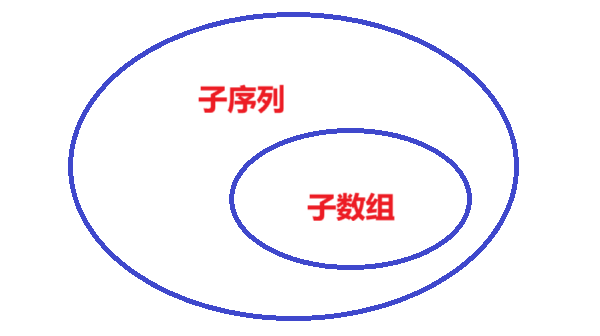
相比之下子序列范围更大，所以也比较难。对子序列 种类暴力枚举的话时间复杂度为 O ( 2 n ) O(2^n) O(2n)，对子数组 种类暴力枚举时间复杂度则是 O ( n 2 ) O(n^2) O(n2)

上题示例所示，数组 [ 10 , 9 , 2 , 5 , 3 , 7 , 101 , 18 ] [10,9,2,5,3,7,101,18] [10,9,2,5,3,7,101,18]，其中单个元素就能构成一个子序列，又或者是 [ 2 , 5 ] 、 [ 2 , 5 , 7 ] 、 [ 2 , 5 , 7 , 101 ] 、 [ 2 , 5 , 7 , 18 ] 、 [ 5 , 7 ] 、 [ 5 , 7 , 101 ] . . . . . . [2,5]、[2,5,7]、[2,5,7,101]、[2,5,7,18]、[5,7]、 [5,7,101] ...... [2,5]、[2,5,7]、[2,5,7,101]、[2,5,7,18]、[5,7]、[5,7,101]......

最长的递增子序列是 [ 2 , 5 , 7 , 101 ] [2,5,7,101] [2,5,7,101]或 [ 2 , 5 , 7 , 18 ] [2,5,7,18] [2,5,7,18]，长度为 4 4 4。

算法原理

在剔除复杂度为 O ( 2 n ) O(2^n) O(2n)外的暴力枚举外，大家第一想到的也许是递归，每个元素都有两种选择，同样复杂度依旧为 O ( 2 n ) O(2^n) O(2n)，不过我们可以进行优化为记忆递归，时间复杂度为 O ( n 2 ) O(n^2) O(n2)，空间复杂度 O ( n 2 ) O(n^2) O(n2)，但题目并未要求得到最长的子序列的每一个元素。我们不必为此大动干戈。

要知道递归和动态规划通常可以互相转化。在讲动态规划之前需要说明一下，动态规划并不是该题的最优解，复杂度为 O ( n 2 ) O(n^2) O(n2)，而最优解是贪心算法，时间复杂度为 O ( n log ⁡ n ) O(n \log n) O(nlogn)，这里不做扩展。

确定状态表示

子数组子序列类型的动规题，我们可以尝试这里做状态表示：

以某个位置为结尾的 . . . . . . ...... ......

所以我们做：

d p [ i ] dp[i] dp[i]表示：以 i i i位置为结尾的所有子序列中最长的递增子序列

至于该状态表示是否正确，取决于是否能推导出正确的状态转移方程。

状态转移方程

以如何构成这个子序列来分析问题。

d p [ i ] = 1 dp[i] = 1 dp[i]=1， i i i位置的元素单独成子序列
d p [ i ] = 1 + max ⁡ ( d p [ j ] ) dp[i] = 1 + \max(dp[j]) dp[i]=1+max(dp[j])，其中 j ∈ [ 0 , i − 1 ] j \in [0, i-1] j∈[0,i−1] 且 n u m s [ j ] < n u m s [ i ] nums[j] < nums[i] nums[j]<nums[i]，跟在前面的 j j j元素为结尾的子序列后面，组成新的序列。

初始化
所有值初始化为最差的情况，即 1 1 1。那么 i i i位置的元素单独成子序列就不用再考虑
填表顺序
填写i位置时需要用到它之前的j位置，所以从前往后填表
返回值
最长递增子序列可以以任意一个位置为结尾，所以最终结果是 d p dp dp表里面的最大值

代码示例

c 复制代码

class Solution {
public:
    int lengthOfLIS(vector<int>& nums)
    {
        int n = nums.size();
        vector<int> dp(n,1);
        for(int i=0;i<n;i++)
        {
            int k = 0;
            for(int j=0;j<i;j++)
                if(nums[j]<nums[i]) k = max(k,dp[j]);
            dp[i] += k;
        }    
        int ret = 0;
        for(auto val:dp) ret = max(val,ret);
        return ret; 
    }
};

二、等差数列划分II-子序列

题目解析

该题是 "子序列 + 等差数列" 的结合题型，相比 "等差数列划分 I（子数组）"（要求连续元素），本题子序列的非连续性大幅提升了难度 ------ 不仅需要统计所有满足条件的子序列，还需避免重复计数，核心考点是动态规划状态的 "维度扩展"（从一维到二维）与哈希表的优化应用。

等差，即相邻元素的差相同。注意至少得有三个元素才能组成等差子序列，所以1个元素和2个元素构成的子序列就不用考虑了。

以题目示例 nums = [2,4,6,8,10] 为例：

先分类统计不同长度的等差子序列：

长度为 3：[2,4,6]（差值 2）、[2,6,10]（差值 4）、[4,6,8]（差值 2）、[6,8,10]（差值 2），共 4 个；
长度为 4：[2,4,6,8]（差值 2）、[4,6,8,10]（差值 2），共 2 个；
长度为 5：[2,4,6,8,10]（差值 2），共 1 个；
总计：4+2+1=7 个，与题目示例输出一致。
隐藏细节：若数组中有重复元素（如 [2,2,2]），则 [2,2,2] 是合法等差子序列（差值 0），需正常统计。

算法原理

状态表示

同样的尝试使用老套路：

d p [ i ] dp[i] dp[i]表示：以 i i i位置结尾的所有的子序列中，等差子序列的个数。

在推导状态转移方程时，我们发现 i i i 位置无法确定是否能接在前一个子序列后面，我们无法知道前面的子序列长什么样，只知道子序列个数。所以该状态表示根本推不出正确的状态转移方程。

根据需求这个状态表示既要能知道子序列个数，又需要知道该子序列长什么样，事实上也很简单，只需要知道最后的两个元素就能知道整个等差子序列，所以多加一位即可。

d p [ i ] [ j ] dp[i][j] dp[i][j]：以i位置和j位置元素结尾的所有子序列中，等差子序列的个数。

状态转移方程

设：

a = n u m s [ k x ] 、 b = n u m s [ i ] 、 c = n u m s [ j ] a=nums[k_x]、b=nums[i]、c=nums[j] a=nums[kx]、b=nums[i]、c=nums[j]

若等差子序列： . . . . . . ...... ...... a a a b b b c c c 则：

b − a = c − b ⇒ a = 2 ∗ b − c b-a=c-b\Rightarrow a=2*b-c b−a=c−b⇒a=2∗b−c

其中： a a a用 k x k_x kx下标是因为 a a a这个值可能有多个，因为要满足子序列的要求所以： k x < i < j k_x<i<j kx<i<j

前面的 a a a值可能有多个该怎么考虑呢？因为题目要求的是统计个数，所以全部的a值都需要考虑，如果只用得到最长的子序列就只需要考虑最后一个a值。

在 i , j i,j i,j结尾的子序列，相当于在 k x k_x kx， i i i结尾的子序列后面加 j j j，所以在填写 d p [ i ] [ j ] dp[i][j] dp[i][j]时，只需要把所有的 d p [ k x ] [ i ] dp[k_x][i] dp[kx][i]相加。此外 k x k_x kx， i i i， j j j也单独构成了一个等差子序列，所以还需要加 1 1 1

即：

d p [ i ] [ j ] = ∑ k = 0 i ( d p [ k ] [ i ] + 1 ) 其中 n u m s [ k ] = 2 ∗ n u m s [ i ] − n u m s [ j ] dp[i][j] = \sum_{k=0}^{i}(dp[k][i]+1)\quad \text{其中 }nums[k]=2*nums[i]-nums[j] dp[i][j]=∑k=0i(dp[k][i]+1)其中 nums[k]=2∗nums[i]−nums[j]

怎么找到 a a a？，如果遍历的话则会增大复杂度，即 O ( n 3 ) O(n^3) O(n3)。为解决这个问题我们可以做这样的优化，在 d p dp dp之前，将所有元素和它的下标数组绑定在一起，放在哈希表中，优化复杂度。

初始化

在最开始两元素是不能构成等差子序列的，所以初始化为 0 0 0。

填表顺序

对 j j j一一枚举，在内嵌一个循环枚举 i i i（注意 i < j i<j i<j），从左往右填写。

返回值

所有 d p dp dp值之和

代码示例

c 复制代码

class Solution {
public:
    int numberOfArithmeticSlices(vector<int>& nums) {
        int n = nums.size(),ret = 0;
        unordered_map<long long,vector<long long>> hash;
        for(int i=0;i<n;i++)
            hash[nums[i]].push_back(i);
        vector<vector<long long>> dp(n,vector<long long>(n,0));
        for(int j=0;j<n;j++)
        {
            for(int i=0;i<j;i++)
            {
                
                long long a = (long long)2*nums[i]-nums[j];
                for(auto k:hash[a])
                    if(k<i) dp[i][j] += 1 + dp[k][i];
                ret+=dp[i][j];
            }
        }
        return ret;
    }
};

双序列问题的输入有两个或更多的序列，通常是两个字符串或数组。由于输入是两个序列，因此状态转移方程通常有两个参数，即 d p [ i ] [ j ] dp[i][j] dp[i][j]，定义第 1 1 1个序列中下标从0到i的子序列和第 2 2 2个序列中下标从 0 0 0到 j j j的子序列的最优解（或解的个数）。一旦找到了 d p [ i ] [ j ] dp[i][j] dp[i][j]与 d p [ i − 1 ] [ j − 1 ] 、 d p [ i − 1 ] [ j ] dp[i-1][j-1]、dp[i-1][j] dp[i−1][j−1]、dp[i−1][j]和 d p [ i ] [ j − 1 ] dp[i][j-1] dp[i][j−1]的关系，通常问题也就迎刃而解。

由于双序列的状态转移方程有两个参数，因此通常需要使用一个二维数组来保存状态转移方程的计算结果。但在大多数情况下，可以优化代码的空间效率，只需要保存二维数组中的一行就可以完成状态转移方程的计算，因此可以只用一个一维数组就能实现二维数组的缓存功能。

接下来通过两个编程题目来介绍如何应用动态规划来解决双序列问题。

三、最长公共子序列

题目解析

最长公共子序列（LCS）是双序列动态规划的 "基石题型"，广泛应用于文本相似度对比（如 DNA 序列匹配、文档 diff 工具）等场景。其核心是理解 "两个序列的同步遍历" 与 "公共元素的非连续性"，通过二维动态规划将双序列问题拆解为子问题，避免暴力枚举的指数级复杂度。

问题定义：给定两个字符串 text1 和 text2，找到它们最长的公共子序列（子序列在两个字符串中相对位置不变，无需连续），返回该子序列的长度。若不存在公共子序列，则返回 0。
关键区分：与 "最长公共子数组（子串）" 不同，公共子序列允许元素不连续。例如 text1 = "abcde"、text2 = "ace"，最长公共子序列是 ace（长度 3），而最长公共子数组是 a 或 c 或 e（长度 1）；若 text1 = "abc"、text2 = "def"，则无公共子序列，返回 0。

算法原理

状态表示

尝试把转化为大问题转化为子问题，这也是递归和动态规划惯用的思路，如下：

( 1 ) . (1). (1).选取第一个字符串 [ 0 , i ] [0,i] [0,i]区间，和第二个字符串 [ 0 , j ] [0,j] [0,j]区间作为研究对象

( 2 ) . (2). (2).根据题目要求，确认状态表示

d p [ i ] [ j ] dp[i][j] dp[i][j]表示： t e x t 1 text1 text1中 [ 0 , i ] [0,i] [0,i]区间以及 t e x t 2 text2 text2中 [ 0 , j ] [0,j] [0,j]区间内所有的子序列中，最长的公共子序列的长度。

状态转移方程

根据最后一个位置的状况，分情况讨论：

相同字符结尾：那么它最长的公共子序列一定是以这两个字符结尾的，在 [ 0 , i − 1 ] ， [ 0 , j − 1 ] [0,i-1]，[0,j-1] [0,i−1]，[0,j−1]找最长公共子序列长度加1即可。
不同字符结尾：那么就只用考虑 [ 0 , i − 1 ] [0,i-1] [0,i−1]和 [ 0 , j ] [0,j] [0,j]区间、 [ 0 , i ] [0,i] [0,i]和 [ 0 , j − 1 ] 、 [ 0 , i − 1 ] [0,j-1]、[0,i-1] [0,j−1]、[0,i−1]和 [ 0 , j − 1 ] [0,j-1] [0,j−1]（该情况已经被前面两种情况包含，不用考虑）

所以状态转移方程：

d p [ i ] [ j ] = { d p [ i − 1 ] [ j − 1 ] + 1 , t e x t 1 [ i ] = = t e x t 2 [ j ] m a x ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − 1 ] ) , t e x t 1 [ i ] ! = t e x t 2 [ j ] dp[i][j]=\begin{cases} dp[i-1][j-1]+1 & \text{},text1[i]==text2[j] \\ max(dp[i-1][j],dp[i][j-1]) & \text{},text1[i]!=text2[j] \end{cases} dp[i][j]={dp[i−1][j−1]+1max(dp[i−1][j],dp[i][j−1]),text1[i]==text2[j],text1[i]!=text2[j]

初始化

关于字符串的 d p dp dp问题，空串是有研究意义的。空串也是公共子序列，只不过长度是 0 0 0而已。

因为状态转移方程中涉及 i − 1 ， j − 1 i-1，j-1 i−1，j−1，我们添加一行一列可以减少了为防止越界而做特殊判断带来的成本，相当于引入空串方便初始化。需要保证两点：

里面的值要保证后续填表是正确的。
下标映射关系。小技巧：可以在每个字符串前面加空格，我们直接从 ( 1 , 1 ) (1,1) (1,1)开始填写所以空格字符不会被考虑。

填表顺序

从上往下，从左往右

返回值

d p dp dp表右下角的值，即 d p [ n ] [ m ] dp[n][m] dp[n][m]

代码示例

c 复制代码

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int n=text1.size(),m=text2.size();
        text1=" "+text1;
        text2=" "+text2;
        vector<vector<int>> dp(n+1,vector<int>(m+1,0));
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                if(text1[i]==text2[j])
                    dp[i][j]=dp[i-1][j-1]+1;
                else
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1]); 
            }
        }
        return dp[n][m];
    }
};

可以注意我们最终要的是 d p [ n ] [ m ] dp[n][m] dp[n][m]的值，其他都不重要。而在得到这个值的过程却需要我们消耗很多空间。接下来讲解一下空间优化思路：

初步优化：填写 d p [ i ] [ j ] dp[i][j] dp[i][j]只需要左边，上边，左上角的值，往上两行后的值就没有利用价值了，而往下几行的空间也暂时用不到。所以只需要用两行就能完成 d p dp dp表的填写，需要两行循环往复的利用，重复一个导一个前面。

进一步优化：我们尝试把优化成一行，可以发现，当 d p dp dp表填写完 d p [ i ] [ j ] dp[i][j] dp[i][j]后，只有 d p [ i − 1 ] [ j ] dp[i-1][j] dp[i−1][j]这个位置及往右的元素是有用的，而 d p [ i ] [ j ] dp[i][j] dp[i][j]往右的空间暂时是空闲的，所以可以把原本需要填到上面的元素填在该行后面不用的空间就可以省下一行的空间。

大多数情况，空间复杂度的优化都没太大意义，重点还是放在时间复杂度上，很多二维 d p dp dp 问题都可以进行类似的空间优化，后续不再赘述。

四、正则表达式匹配

题目解析

该题是正则表达式基础语法的 "算法实现题"，核心考点是动态规划对 "模糊匹配规则" 的处理 ------ 通过状态定义覆盖 ′ . ′ '.' ′.′（任意字符匹配）和 ′ ∗ ′ '*' ′∗′（零或多个前导字符匹配）的所有场景，同时避免回溯法的高复杂度，是面试中难度较高的双序列动态规划题目。

该题的规律比较抽象，我们来一一理一下：

提供两个字符串 s s s和 p p p， s s s是普通的 a a a~ z z z的小写字母，而 p p p字符串里面除了小写字母还有 ′ . ′ '.' ′.′和 ′ ∗ ′ '*' ′∗′。

让两个字符串进行匹配，其中

′ . ′ '.' ′.′可用替代任何字符。例如 ′ . a ′ '.a' ′.a′可以匹配 ′ z a ′ 'za' ′za′（ ′ . ′ '.' ′.′代替字符 ′ z ′ 'z' ′z′）
′ ∗ ′ ' * ' ′∗′可以匹配零个或多个前面的字符。例如 " a b ∗ c " "ab*c" "ab∗c"可以匹配： " a c " "ac" "ac"（ " b ∗ " "b*" "b∗" 匹配 0 0 0 个 b b b），或 " a b ∗ c " "ab*c" "ab∗c"可以匹配： " a b b b c " "abbbc" "abbbc"（ " b ∗ " "b*" "b∗" 匹配 3 3 3 个 b b b）

当然了还可以".*"这样搭配，而且它可以匹配所有字符串，包括空串。注意： " . ∗ " ".* " ".∗"并不是.先替代任何一个字符，然后 ′ ∗ ′ '*' ′∗′在匹配零个或多个该字符。而是 ′ ∗ ′ '*' ′∗′可以以匹配零个或多个前面的字符 ′ . ′ '.' ′.′。这样理解才能把题做对。

提示内容也值得我们注意，字符串中只会出现小写字母、 ′ . ′ '.' ′.′和 ′ ∗ ′ '*' ′∗′，而且*号前一定有有效字符（也就是不可能出现 " ∗ ∗ " "**" "∗∗"）

算法原理

状态表示

同样的拆分为小问题：

d p [ i ] [ j ] dp[i][j] dp[i][j]：表示 s [ 0 , i ] s[0,i] s[0,i]区间的子串是否能匹配 p [ 0 , j ] p[0,j] p[0,j]区间内的子串。能匹配为true，不能则为false

状态转移方程

根据最后一个位置的状态，分情况讨论，在填写到 d p [ i ] [ j ] dp[i][j] dp[i][j]时， p [ j ] p[j] p[j]可能有以下情况：

( 1 ) (1) (1) ' a 'a 'a~ z ' z' z'：最后一个必须相等才能匹配，并且判断 dp [i-1][j-1] 为 true 即可，否则不匹配
( 2 ) (2) (2) ' . ' '.' '.'：因为'.'能替代任何字符所以最后两个一定相等，所以与上同，判断 dp [i-1][j-1] 为 true 即可，否则不匹配
( 3 ) (3) (3) ' ∗ ' '*' '∗'：必须和前面字符搭配使用，但前面字符又要根据p[j-1]可能的值分类。

继续情况 ( 3 ) (3) (3)，又需要分两类，即：
情形一： p [ j − 1 ] p[j-1] p[j−1]= ' . ' '.' '.'

而 " . ∗ " ".*" ".∗"可翻译成空、一个点、两个点、三个点...多种情况，那么dp[i][j]为：
d p [ i ] [ j ] = { d p [ i ] [ j − 2 ] d p [ i − 1 ] [ j − 2 ] d p [ i − 2 ] [ j − 2 ] d p [ i − 3 ] [ j − 2 ] . . . . . . dp[i][j]=\begin{cases} dp[i][j-2] \\ dp[i-1][j-2] \\ dp[i-2][j-2] \\ dp[i-3][j-2] \\ ...... \end{cases} dp[i][j]=⎩ ⎨ ⎧dp[i][j−2]dp[i−1][j−2]dp[i−2][j−2]dp[i−3][j−2]......

然而只需要任意一个中情况为true即可，即

d p [ i ] [ j ] = d p [ i ] [ j − 2 ] ∣ ∣ d p [ i − 1 ] [ j − 2 ] ∣ ∣ d p [ i − 2 ] [ j − 2 ] ∣ ∣ . . . . . . dp[i][j]=dp[i][j-2]||dp[i-1][j-2]||dp[i-2][j-2]||...... dp[i][j]=dp[i][j−2]∣∣dp[i−1][j−2]∣∣dp[i−2][j−2]∣∣......

但此时时间复杂度已经达到了 O ( n 3 ) O(n^3) O(n3)，必须得优化，看这些状态能否由若干个状态代替。

又两种思路：

数学

对上式的 i i i减 1 1 1得 d p [ i − 1 ] [ j ] dp[i-1][j] dp[i−1][j]的表达式：

d p [ i − 1 ] [ j ] = d p [ i − 1 ] [ j − 2 ] ∣ ∣ d p [ i − 2 ] [ j − 2 ] ∣ ∣ d p [ i − 3 ] [ j − 2 ] ∣ ∣ . . . . . . dp[i-1][j]=dp[i-1][j-2]||dp[i-2][j-2]||dp[i-3][j-2]||...... dp[i−1][j]=dp[i−1][j−2]∣∣dp[i−2][j−2]∣∣dp[i−3][j−2]∣∣......

结合两个式子得：

d p [ i ] [ j ] = d p [ i ] [ j − 2 ] ∣ ∣ d p [ i − 1 ] [ j ] dp[i][j]=dp[i][j-2]||dp[i-1][j] dp[i][j]=dp[i][j−2]∣∣dp[i−1][j]

状态表示结合实际情况，优化状态转移方程

假设当前有多个 " . ∗ " ".*" ".∗"，在此匹配掉一个后，留给dp[i-1][j]去匹配，所以同样得：

d p [ i ] [ j ] = d p [ i ] [ j − 2 ] ∣ ∣ d p [ i − 1 ] [ j ] dp[i][j]=dp[i][j-2]||dp[i-1][j] dp[i][j]=dp[i][j−2]∣∣dp[i−1][j]

情形二： p [ j − 1 ] p[j-1] p[j−1]= ' a 'a 'a~ z ' z' z' ：

翻译成空串：然后只用考虑 d p [ i ] [ j − 2 ] dp[i][j-2] dp[i][j−2]
匹配掉一个，然后保留给 s [ i − 1 ] s[i-1] s[i−1]，即 p [ j − 1 ] = = s [ i ] & & d p [ i − 1 ] [ j ] p[j-1]==s[i]\&\&dp[i-1][j] p[j−1]==s[i]&&dp[i−1][j]

综上状态转移方程为：

d p [ i ] [ j ] = { ( p [ j ] = = s [ i ] ∣ ∣ p [ j ] = = ′ . ′ ) & & d p [ i − 1 ] [ j − 1 ] 其中 p [ j ] ! = ′ ∗ ′ d p [ i ] [ j − 2 ] ∣ ∣ ( ( p [ j − 1 ] = = ′ . ′ ∣ ∣ p [ j − 1 ] = = s [ i ] ) & & d p [ i − 1 ] [ j ] ) 其中 p [ j ] = = ′ ∗ ′ dp[i][j]=\begin{cases} (p[j]==s[i]||p[j]=='.')\&\&dp[i-1][j-1] &\text{其中}p[j]!='*'\\ dp[i][j-2]||((p[j-1]=='.'||p[j-1]==s[i])\&\&dp[i-1][j] )&\text{其中}p[j]=='*' \end{cases} dp[i][j]={(p[j]==s[i]∣∣p[j]==′.′)&&dp[i−1][j−1]dp[i][j−2]∣∣((p[j−1]==′.′∣∣p[j−1]==s[i])&&dp[i−1][j])其中p[j]!=′∗′其中p[j]==′∗′

根据规律我们可以把整合为两个分支，p[j]等于 ′ ∗ ′ '*' ′∗′和不等于 ′ ∗ ′ '*' ′∗′，或许你看懂了前面的分析当看到最终的第二个式子有些懵，我来解释一下：

在 p [ i ] = = ′ ∗ ′ p[i]=='*' p[i]==′∗′的情况中， d p [ i ] [ j − 2 ] dp[i][j-2] dp[i][j−2]，表示'*'和前面的字符（无论是'a~z'还是'.'）结合成空串的情况， ( p [ j − 1 ] = = ′ . ′ ∣ ∣ p [ j − 1 ] = = s [ i ] ) & & d p [ i − 1 ] [ j ] (p[j-1]=='.'||p[j-1]==s[i])\&\&dp[i-1][j] (p[j−1]==′.′∣∣p[j−1]==s[i])&&dp[i−1][j]表示， ′ ∗ ′ '*' ′∗′结合字母或 ′ . ′ '.' ′.′把s[i]匹配掉后留给s[i-1]的情况。

初始化

为方便初始化和填表不会越界，加一行加一列，但要注意两点：

里面的值要保证后续填表是正确的：
第一列 d p [ i ] [ 0 ] dp[i][0] dp[i][0]：表示 s [ 0 , i ] s[0,i] s[0,i]与 p p p的空串匹配，所以为false，但是 d p [ 0 ] [ 0 ] dp[0][0] dp[0][0]相当于s的空串和p的空串匹配所以为true。
第一行 d p [ 0 ] [ j ] dp[0][j] dp[0][j]：表示 s s s的空串和 p [ 0 , j ] p[0,j] p[0,j]的字符串匹配，如果 p [ 0 , j ] p[0,j] p[0,j]是 " _ ∗ " "\*" "∗"（ ′ _ ′ '\' ′′表示任意字符）就能匹配，为true，不仅如此， p [ 0 , j ] p[0,j] p[0,j]为 _ ∗ _ ∗ _ ∗ . . . . . . \*\*\*...... ∗∗∗......这样的格式的都能匹配空串，也就是这个字符串的++每一个偶数位++ 都是 ′ ∗ ′ '*' ′∗′。
下标映射关系：
在用 s s s和 p p p中的元素时把下标整体减1。
或在 s s s和 p p p前填充一个空格字符来占位。

填表顺序
从上往下，从左往右
返回值
返回dp表的最后一个位置，即 d p [ n ] [ m ] dp[n][m] dp[n][m]

代码示例

c 复制代码

class Solution {
public:
    bool isMatch(string s, string p)
    {
        int n=s.size(),m=p.size();
        s=" "+s,p=" "+p;
        vector<vector<bool>> dp(n+1,vector<bool>(m+1));
        dp[0][0]=true;
        for(int j=1;j<=m;j++)
        {
            if(j%2==0)
            {
                if(p[j]=='*') dp[0][j]=true;
                else break;
            }
        }    
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                if(p[j]!='*') dp[i][j]=(p[j]=='.'||p[j]==s[i])&&dp[i-1][j-1];
                else dp[i][j]=dp[i][j-2]||((p[j-1]=='.'||p[j-1]==s[i])&&dp[i-1][j]);
            }
        }
        return dp[n][m];
    }
};

非常感谢您能耐心读完这篇文章。倘若您从中有所收获，还望多多支持呀！