文章目录
前言
考试方式是邮箱发送网址,进行牛客网线上笔试,四道编程题目,两道标准算法题目,两道实际应用型算法题,本篇博客分享前两道题。(四道题全部写在一起篇幅太大了)
题目1 旋转链表
题目链接:牛客 NC211 旋转链表
题目描述:
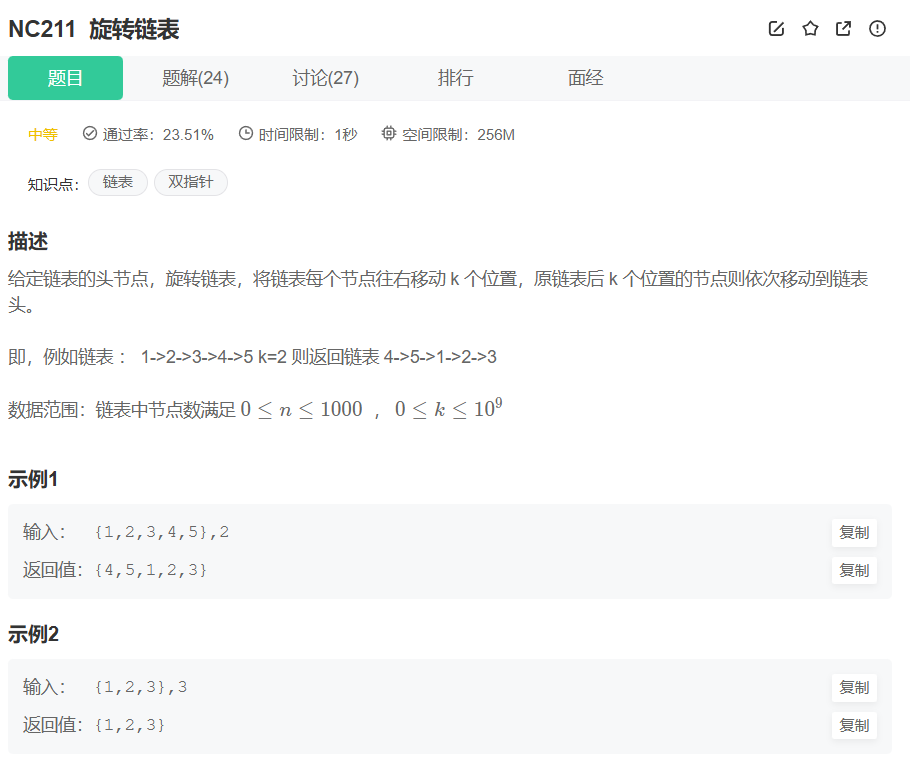
算法分析
链表的旋转操作若直接逐节点移动,会因重复遍历导致时间复杂度达到 O ( k ∗ n ) O(k*n) O(k∗n),这在 k 较大时完全不可行。结合链表的特性,我们可将其转化为环形结构来简化操作:先遍历链表统计长度,将尾节点指向头节点形成环,此时旋转 k 个位置的本质,是找到新头节点的位置并断开环。由于旋转 n 次(n 为链表长度)后链表会回到初始状态,因此我们只需计算 k % n 得到有效旋转次数,再从原头节点向后移动 n - (k % n) 个节点,该节点的下一个节点即为新头节点,断开此处的环即可完成旋转。
代码实现
cpp
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* ListNode(int x) : val(x), next(nullptr) {}
* };
*/
class Solution {
public:
ListNode* rotateLinkedList(ListNode* head, int k) {
// 边界情况:空链表或单节点链表无需旋转,直接返回原头节点
if(head == nullptr || head->next == nullptr)
return head;
ListNode* cur = head;
int size = 1;
// 遍历链表统计长度,同时定位到尾节点
while(cur->next != nullptr)
{
size++;
cur = cur->next;
}
// 将尾节点指向头节点,构建环形链表
cur -> next = head;
// 计算有效旋转次数,避免重复旋转
k %= size;
// 计算需要移动的步数,找到新头节点的前驱节点
int move_step = size - k;
ListNode* mark = head;
// 移动到新头节点的前驱节点
for(int i = 1; i < move_step; i++)
mark = mark->next;
// 确定新头节点并断开环形结构
ListNode* newhead = mark->next;
mark->next = nullptr;
return newhead;
}
};实现细节与实战思考
在实际解题过程中,边界条件的处理是避免出错的关键:空链表或仅有一个节点的链表,无论旋转多少次结果都不变,可直接返回原头节点。构建环形链表时,需确保遍历到真正的尾节点------即 cur->next 为 nullptr 的节点,而非仅遍历到最后一个有值节点。
关于步数计算的细节容易成为易错点:move_step 表示从原头节点到新头节点前驱节点的步数,循环从 1 开始而非 0,是因为初始时 mark 已指向原头节点(对应第1个节点),只需再移动 move_step - 1 次即可到达目标位置。例如链表长度为5、k=2 时,move_step=3,循环执行2次,mark 最终指向第3个节点,其下一个节点即为新头节点。
题目2 广度优先遍历打印二叉树问题
题目链接:牛客 JZ78 把二叉树打印成多行 [ 并不是原题但是比这道题简单,并不用分层,直接就是程序便利输入到一个数组中即可。
传送门:这道题和我今天做的每日一题很像,都是BFS解决二叉树层序遍历的问题,更加详细的解释可以看这篇博客 N 叉树的层序遍历
题目描述:
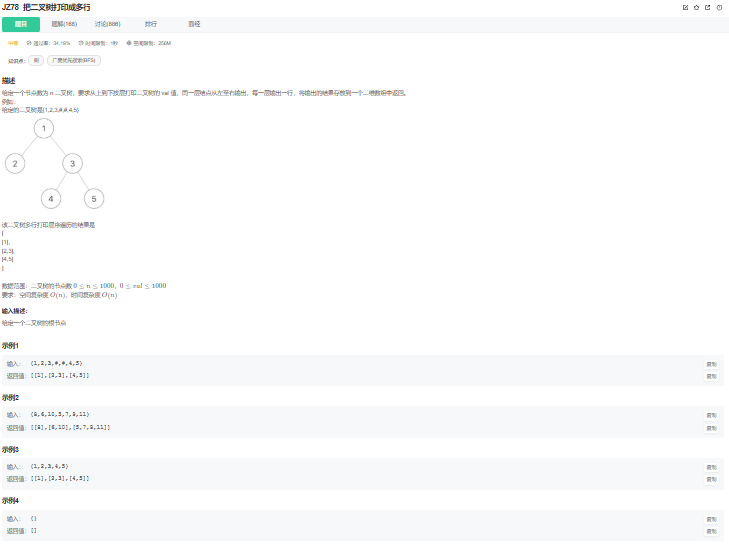
题目背景与核心需求
二叉树的层序遍历是广度优先搜索(BFS)的经典应用,本题要求将二叉树按层打印,每一层的节点值单独存入一个数组,最终返回二维数组结果。不同于普通的层序遍历,本题需要精准区分每一层的节点,避免不同层的节点混在一起,这就要求在遍历过程中对每一层的节点数量进行精准统计。
算法分析
广度优先遍历依赖队列实现,核心思路是利用队列的"先进先出"特性,逐层处理节点。在遍历开始时,先将根节点入队;每一轮循环中,先记录当前队列的大小(即当前层的节点数),再依次取出该数量的节点,将节点值存入当前层的数组,同时将每个节点的左右子节点(若存在)入队。当当前层的所有节点处理完毕后,将该层的数组存入结果集,重复此过程直到队列为空。这种方式能确保每一轮循环仅处理一层节点,天然实现了层与层的分隔。
代码实现
cpp
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
#include <queue>
#include <vector>
class Solution {
public:
vector<vector<int> > Print(TreeNode* pRoot) {
// 存储最终的分层打印结果
vector<vector<int>> ret;
// 边界条件:空树直接返回空结果
if(pRoot == nullptr) return ret;
// 队列用于存储待处理的节点,实现广度优先遍历
queue<TreeNode*> q;
q.push(pRoot);
// 队列非空时,说明还有未处理的节点
while(!q.empty())
{
// 记录当前层的节点数量,这是分层的关键
int level_size = q.size();
// 存储当前层的节点值
vector<int> level_nums;
// 遍历当前层的所有节点
while(level_size--)
{
TreeNode* tmp = q.front();
level_nums.push_back(tmp->val);
q.pop();
// 左子节点存在则入队,为下一层遍历做准备
if(tmp->left != nullptr) q.push(tmp->left);
// 右子节点存在则入队
if(tmp->right != nullptr) q.push(tmp->right);
}
// 将当前层的结果存入最终结果集
ret.push_back(level_nums);
}
return ret;
}
};细节分析与实战思考
队列的使用是本题的核心,其"先进先出"的特性恰好匹配层序遍历"从上到下、从左到右"的顺序。在实际解题时,level_size 的取值时机尤为重要------必须在处理当前层节点前获取队列大小,因为处理节点的过程中会将下一层节点入队,若在循环中获取会导致统计的节点数包含下一层内容。
例如对于一棵三层二叉树,初始时队列仅含根节点,level_size=1,处理完根节点后,其左右子节点入队,此时队列大小变为2;第二轮循环中 level_size=2,处理完这两个节点后,它们的子节点入队,队列大小变为4,以此类推。这种方式能精准划分每一层的节点,避免层序混乱。
此外,边界条件的处理不可忽视:空树的情况下直接返回空的二维数组,避免后续操作中访问空指针导致程序崩溃。在遍历节点时,需先判断左右子节点是否存在,再将其入队,这是防止无效节点入队的必要步骤。
总结
- 旋转链表问题的核心是通过构建环形链表简化旋转操作,结合取模运算优化旋转次数,同时需精准定位新头节点的前驱节点以断开环形结构,边界条件(空链表、单节点链表)的处理是避免错误的关键。
- 二叉树分层打印的核心是利用队列实现广度优先遍历,通过记录每一轮循环前的队列大小区分不同层节点,确保每一轮仅处理当前层节点,子节点入队的时机和顺序决定了遍历的正确性。
- 两道题目均体现了"先优化问题模型,再处理细节"的解题思路:旋转链表将多次旋转转化为环形结构的一次断开,二叉树遍历将"分层"需求转化为队列大小的统计,这种思路能有效降低时间复杂度,提升代码效率。