「深度学习笔记4」深度学习优化算法完全指南：从梯度下降到Adam的实战详解

掌握优化算法，让深度学习模型训练事半功倍

1. 优化算法：深度学习的"智能导航系统"

想象一下，你在一个复杂的地形中寻找最低点（模型的最优解），四周都是高山和山谷（损失函数的复杂曲面）。优化算法就是你的智能导航系统，它能够分析地形坡度（梯度），为你规划最高效的下降路径，避免你陷入局部洼地（局部最优解），最终找到真正的目的地（全局最优解）。

1.1 优化问题的本质：寻找最佳参数

在深度学习中，我们的目标是找到一组模型参数 θ\thetaθ，使得损失函数 J(θ)J(\theta)J(θ) 的值最小。这可以形式化为数学问题：

min⁡θJ(θ)=1m∑i=1mL(f(xi;θ),yi)\min_{\theta} J(\theta) = \frac{1}{m}\sum_{i=1}^{m} L(f(x_i; \theta), y_i)θminJ(θ)=m1i=1∑mL(f(xi;θ),yi)

简单解释：

• θ\thetaθ：模型的所有权重和偏置参数，好比导航系统中的位置坐标
• J(θ)J(\theta)J(θ)：损失函数，衡量模型预测值与真实值的差异，好比地形高度
• LLL：单个样本的损失计算，好比每步的落差测量

2. 基础优化算法详解

2.1 梯度下降法：最基础的"下山方法"

梯度下降法是最直观的优化算法，其核心思想是：沿着坡度最陡的方向下山。

数学原理 ： θt+1=θt−η⋅∇θJ(θt)\theta_{t+1} = \theta_t - \eta \cdot \nabla_\theta J(\theta_t)θt+1=θt−η⋅∇θJ(θt)

其中：

• θt\theta_tθt：当前参数位置
• η\etaη：学习率（步长大小）
• ∇θJ(θt)\nabla_\theta J(\theta_t)∇θJ(θt)：梯度（坡度方向和陡峭程度）

import numpy as np
import matplotlib.pyplot as plt

def simple_gradient_descent():
    """梯度下降法简单示例：寻找函数 y = (x-3)^2 的最小值"""
    
    # 定义损失函数和梯度函数
    def loss_function(x):
        return (x - 3)**2
    
    def gradient(x):
        return 2 * (x - 3)
    
    # 初始化参数
    x = 0.0  # 初始位置
    learning_rate = 0.1  # 学习率（步长）
    iterations = 15  # 迭代次数
    path = []  # 记录路径
    
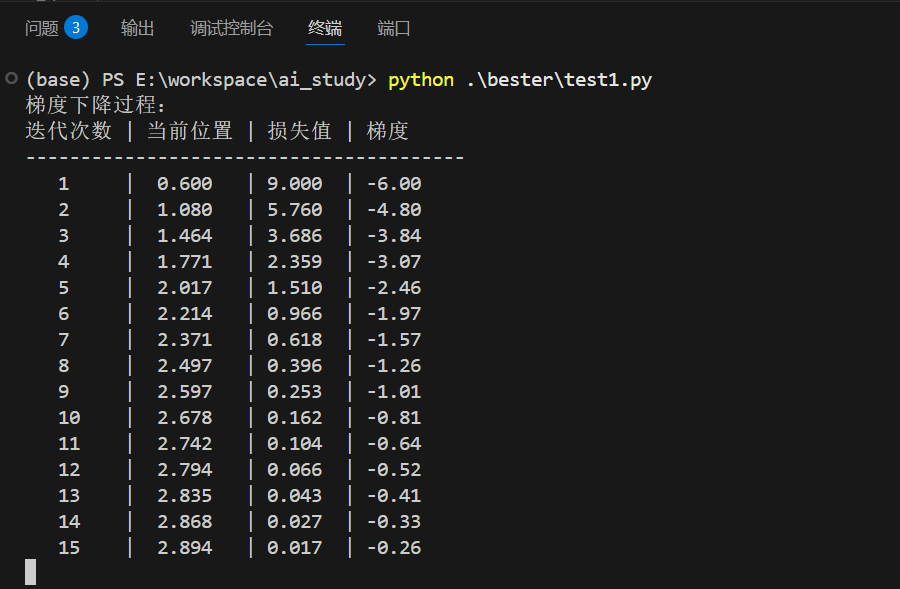
    print("梯度下降过程：")
    print("迭代次数 | 当前位置 | 损失值 | 梯度")
    print("-" * 40)
    
    for i in range(iterations):
        current_loss = loss_function(x)
        current_gradient = gradient(x)
        path.append((x, current_loss))
        
        # 更新位置：新位置 = 旧位置 - 学习率 × 梯度
        x = x - learning_rate * current_gradient
        
        print(f"{i+1:^8} | {x:^8.3f} | {current_loss:^6.3f} | {current_gradient:^5.2f}")
    
    # 可视化优化过程
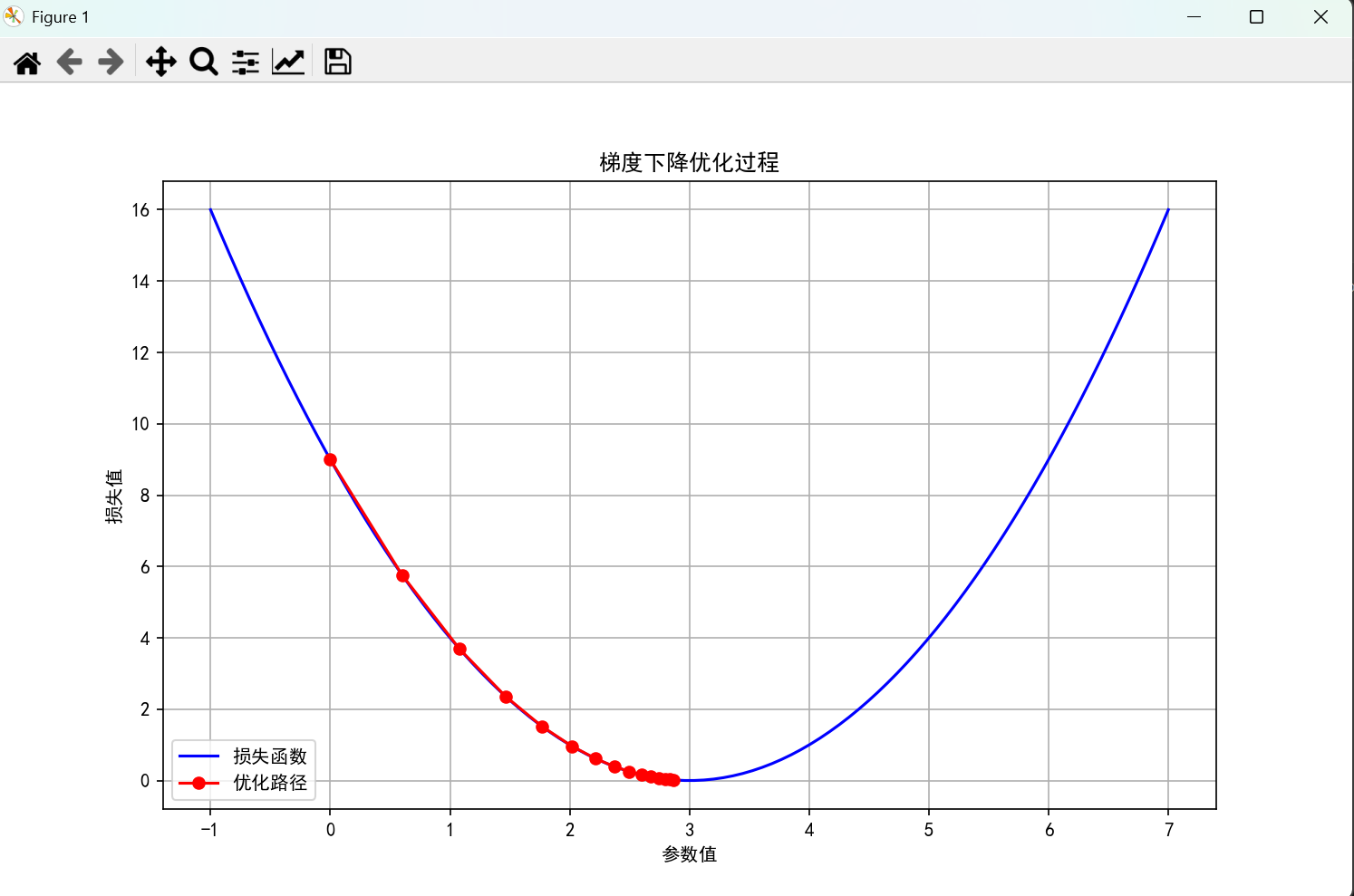
    x_vals = np.linspace(-1, 7, 100)
    y_vals = loss_function(x_vals)
    
    plt.figure(figsize=(10, 6))
    plt.plot(x_vals, y_vals, 'b-', label='损失函数')
    path_x, path_y = zip(*path)
    plt.plot(path_x, path_y, 'ro-', label='优化路径')
    plt.xlabel('参数值')
    plt.ylabel('损失值')
    plt.title('梯度下降优化过程')
    plt.legend()
    plt.grid(True)
    plt.show()
    
    return path

# 运行示例
path = simple_gradient_descent()

运行结果:

2.2 随机梯度下降（SGD）：应对大数据挑战

当训练数据集很大时，计算所有样本的梯度（批量梯度下降）成本太高。随机梯度下降每次只使用一个随机样本计算梯度，大大提高了计算效率。

算法特点：

• ✅ 计算效率高：每次迭代只需计算单个样本梯度
• ✅ 逃离局部最优：随机性有助于跳出局部最小值
• ❌ 收敛不稳定：梯度估计有噪声，收敛路径震荡

import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

def stochastic_gradient_descent(X, y, learning_rate=0.01, epochs=100):
    """随机梯度下降实现线性回归"""
    # 初始化参数
    w = np.random.randn(X.shape[1])
    b = 0
    losses = []
    for epoch in range(epochs):
        total_loss = 0
        # 随机打乱数据
        indices = np.random.permutation(len(X))
        for i in indices:
            # 单个样本的前向传播和损失计算
            y_pred = np.dot(X[i], w) + b
            loss = (y_pred - y[i])**2
            # 计算单个样本的梯度[6]
            dw = 2 * (y_pred - y[i]) * X[i]
            db = 2 * (y_pred - y[i])
            # 更新参数
            w = w - learning_rate * dw
            b = b - learning_rate * db
            total_loss += loss
        avg_loss = total_loss / len(X)
        losses.append(avg_loss)
        if epoch % 20 == 0:
            print(f'Epoch {epoch}, Loss: {avg_loss:.4f}')
    return w, b, losses

# 1. 生成模拟数据
np.random.seed(42)  # 设置随机种子确保结果可重现
X = 2 * np.random.rand(100, 1)  # 生成100个样本，特征范围[0, 2]
true_w = 3  # 真实权重
true_b = 4   # 真实偏置
y = true_b + true_w * X + np.random.randn(100, 1) * 0.5  # 添加噪声
  
# 确保y是一维数组
y = y.flatten()

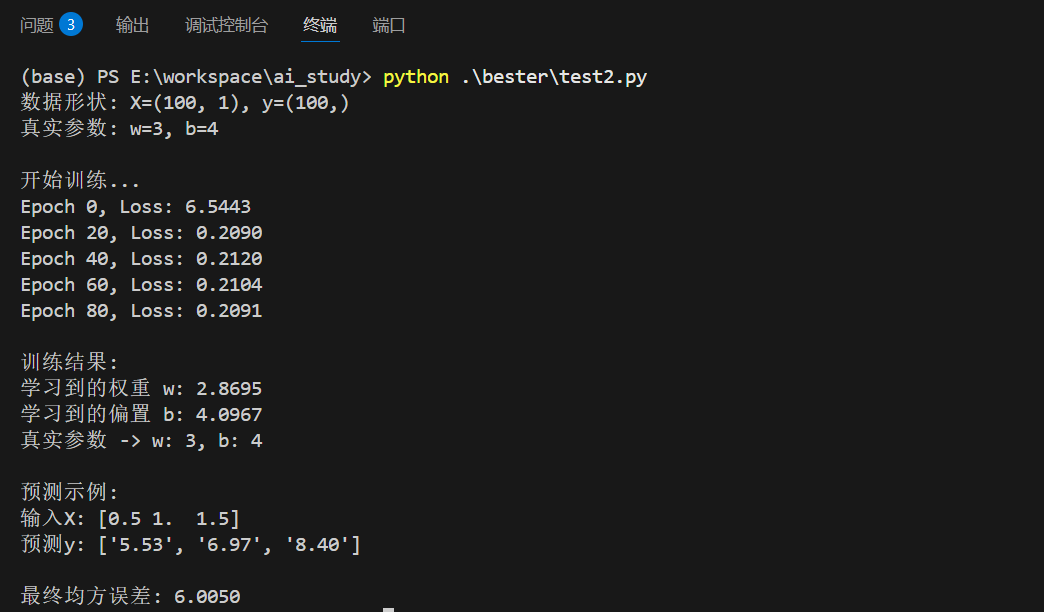
print(f"数据形状: X={X.shape}, y={y.shape}")
print(f"真实参数: w={true_w}, b={true_b}")

# 2. 运行随机梯度下降
print("\n开始训练...")
w_trained, b_trained, loss_history = stochastic_gradient_descent(
    X, y, learning_rate=0.01, epochs=100
)
print(f"\n训练结果:")
print(f"学习到的权重 w: {w_trained[0]:.4f}")
print(f"学习到的偏置 b: {b_trained:.4f}")
print(f"真实参数 -> w: {true_w}, b: {true_b}")

# 3. 可视化结果
plt.figure(figsize=(15, 5))

# 子图1: 原始数据和拟合直线
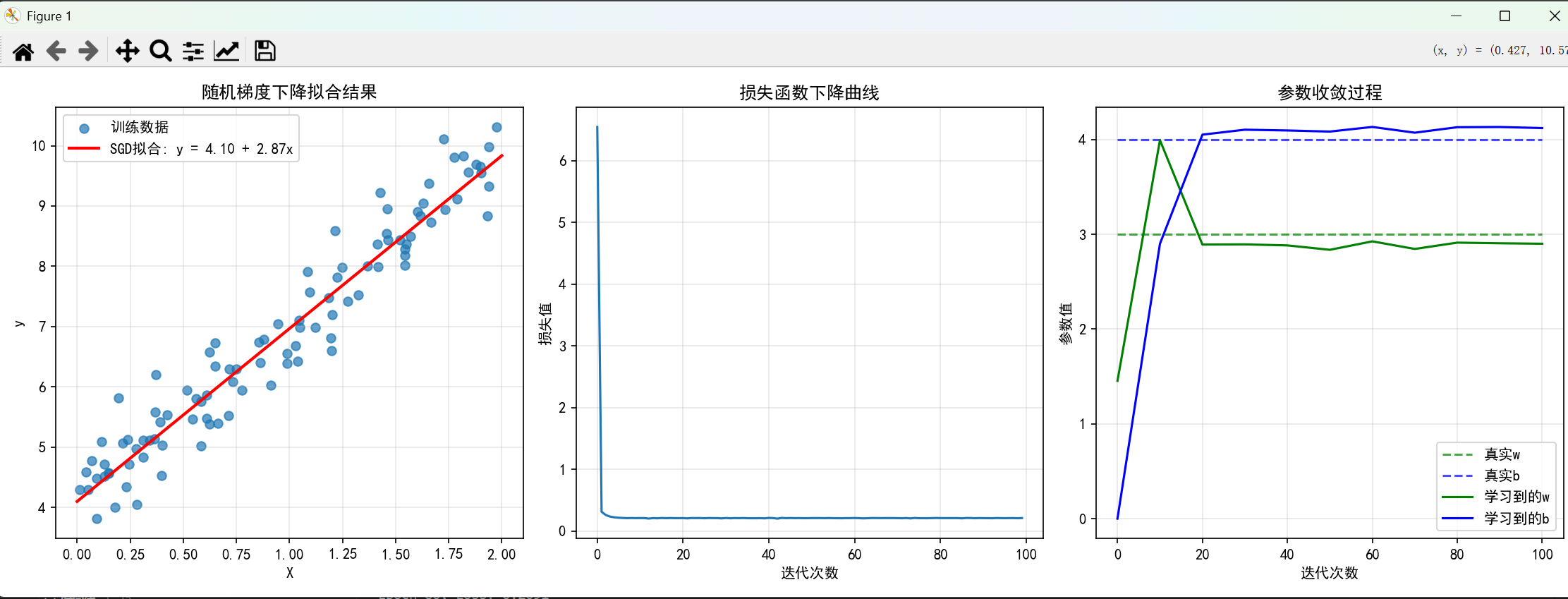
plt.subplot(1, 3, 1)
plt.scatter(X, y, alpha=0.7, label='训练数据')
x_range = np.array([[0], [2]])

y_pred = w_trained[0] * x_range + b_trained

plt.plot(x_range, y_pred, 'r-', linewidth=2, label=f'SGD拟合: y = {b_trained:.2f} + {w_trained[0]:.2f}x')
plt.xlabel('X')
plt.ylabel('y')
plt.title('随机梯度下降拟合结果')
plt.legend()
plt.grid(True, alpha=0.3)

# 子图2: 损失下降曲线
plt.subplot(1, 3, 2)
plt.plot(loss_history)
plt.xlabel('迭代次数')
plt.ylabel('损失值')
plt.title('损失函数下降曲线')
plt.grid(True, alpha=0.3)

# 子图3: 参数收敛过程（需要修改函数来记录参数历史）
plt.subplot(1, 3, 3)

# 为了演示，我们重新运行一次并记录参数
def sgd_with_tracking(X, y, learning_rate=0.01, epochs=100):
    w = np.random.randn(X.shape[1])
    b = 0
    w_history, b_history = [w.copy()], [b]
    for epoch in range(epochs):
        indices = np.random.permutation(len(X))
        for i in indices:
            y_pred = np.dot(X[i], w) + b
            dw = 2 * (y_pred - y[i]) * X[i]
            db = 2 * (y_pred - y[i])
            w -= learning_rate * dw
            b -= learning_rate * db
        if epoch % 10 == 0:  # 每10轮记录一次
            w_history.append(w.copy())
            b_history.append(b)
    return w, b, w_history, b_history

w_final, b_final, w_hist, b_hist = sgd_with_tracking(X, y)
epochs_plot = range(0, 101, 10)
plt.plot(epochs_plot, [true_w] * len(epochs_plot), 'g--', label='真实w', alpha=0.7)
plt.plot(epochs_plot, [true_b] * len(epochs_plot), 'b--', label='真实b', alpha=0.7)
plt.plot(epochs_plot, [w[0] for w in w_hist], 'g-', label='学习到的w')
plt.plot(epochs_plot, b_hist, 'b-', label='学习到的b')
plt.xlabel('迭代次数')
plt.ylabel('参数值')
plt.title('参数收敛过程')
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()

# 4. 模型预测示例
print("\n预测示例:")
test_X = np.array([[0.5], [1.0], [1.5]])
print("输入X:", test_X.flatten())
predictions = w_trained[0] * test_X + b_trained
print("预测y:", [f'{p[0]:.2f}' for p in predictions])

# 计算最终误差

final_predictions = w_trained[0] * X + b_trained

final_loss = np.mean((final_predictions - y) ** 2)

print(f"\n最终均方误差: {final_loss:.4f}")

运行结果:

3. 高级优化算法：更智能的导航策略

3.1 动量法：带"惯性"的下山

动量法模拟物理中的动量概念，积累历史梯度信息来加速收敛并减少震荡。

算法原理 ： vt=γvt−1+η∇θJ(θt)v_t = \gamma v_{t-1} + \eta \nabla_\theta J(\theta_t)vt=γvt−1+η∇θJ(θt) θt+1=θt−vt\theta_{t+1} = \theta_t - v_tθt+1=θt−vt

其中 γ\gammaγ 是动量系数（通常为0.9），vtv_tvt 是动量项。

def momentum_gradient_descent():
    """动量梯度下降示例"""
    
    def loss_function(x):
        return (x - 3)**2 + 0.5 * np.sin(10*x)  # 添加波动模拟复杂地形
    
    def gradient(x):
        return 2*(x-3) + 5*np.cos(10*x)  # 复杂梯度
    
    # 参数初始化
    x = 0.0
    learning_rate = 0.05
    gamma = 0.9  # 动量系数
    velocity = 0  # 速度项
    iterations = 50
    path = []
    
    print("动量梯度下降 vs 普通梯度下降")
    print("迭代次数 | 动量法位置 | 普通法位置")
    print("-" * 40)
    
    # 对比普通梯度下降
    x_normal = 0.0
    
    for i in range(iterations):
        # 动量法
        grad = gradient(x)
        velocity = gamma * velocity + learning_rate * grad
        x = x - velocity
        
        # 普通梯度下降
        grad_normal = gradient(x_normal)
        x_normal = x_normal - learning_rate * grad_normal
        
        path.append((x, x_normal))
        
        if i % 10 == 0:
            print(f"{i:^8} | {x:^10.3f} | {x_normal:^10.3f}")
    
    return path

3.2 Adam算法：自适应学习率的智能优化器

Adam（Adaptive Moment Estimation）结合了动量法和自适应学习率的优点，是当前最流行的优化算法。

算法步骤：

1. 计算梯度的一阶矩估计（动量）
2. 计算梯度的二阶矩估计（自适应学习率）
3. 进行偏差校正
4. 更新参数

import torch
import torch.optim as optim

def adam_optimizer_demo():
    """Adam优化器实战示例"""
    
    # 创建简单的线性回归模型
    model = torch.nn.Sequential(
        torch.nn.Linear(10, 50),  # 输入10维，隐藏层50维
        torch.nn.ReLU(),
        torch.nn.Linear(50, 1)    # 输出1维
    )
    
    # 使用Adam优化器
    optimizer = optim.Adam(model.parameters(), 
                          lr=0.001,      # 学习率
                          betas=(0.9, 0.999),  # 一阶和二阶矩衰减率
                          eps=1e-8)      # 数值稳定性常数
    
    # 模拟训练过程
    losses = []
    for epoch in range(100):
        # 生成模拟数据
        inputs = torch.randn(32, 10)  # 批量大小32
        targets = torch.randn(32, 1)
        
        # 前向传播
        outputs = model(inputs)
        loss = torch.nn.functional.mse_loss(outputs, targets)
        
        # 反向传播
        optimizer.zero_grad()  # 清零梯度
        loss.backward()        # 计算梯度
        optimizer.step()       # 更新参数
        
        losses.append(loss.item())
        
        if epoch % 20 == 0:
            print(f'Epoch {epoch}, Loss: {loss.item():.4f}')
    
    return losses

# 运行Adam示例
losses = adam_optimizer_demo()

4. 优化算法对比与选择指南

表：主要优化算法特性全面对比

算法	核心思想	优点	缺点	适用场景	调参要点
梯度下降	沿负梯度方向更新	稳定收敛，理论成熟	速度慢，易陷局部最优	小规模凸优化问题	学习率选择关键
随机梯度下降	随机样本梯度估计	计算高效，逃离局部最优	收敛不稳定，震荡明显	大规模数据集训练	需要学习率调度
动量法	积累历史梯度信息	减少震荡，加速收敛	需要调整动量参数	深层次网络训练	动量系数0.9
Adam	自适应学习率+动量	收敛快，参数鲁棒性强	可能错过精细结构	大多数深度学习任务	默认参数效果佳
RMSProp	自适应调整学习率	处理非平稳目标效果好	对初始学习率敏感	RNN、LSTM等序列模型	衰减率设置重要

5. 学习率调度：动态调整步长策略

学习率是优化算法中最重要的超参数。合适的学习率调度策略能显著提高训练效果。

5.1 常见学习率调度器实战

import torch
import torch.nn as nn
from torch.optim import SGD
from torch.optim.lr_scheduler import StepLR
  
# 1. 定义一个极简的线性模型（用于演示）
model = nn.Linear(in_features=10, out_features=1)  # 输入10维，输出1维

# 2. 定义优化器（初始学习率设为0.1）
optimizer = SGD(model.parameters(), lr=0.1)
# 3. 定义StepLR调度器：每5个epoch将学习率乘以0.1（即降为原来的10%）
scheduler = StepLR(optimizer, step_size=5, gamma=0.1)
# 4. 模拟训练循环（共10个epoch）
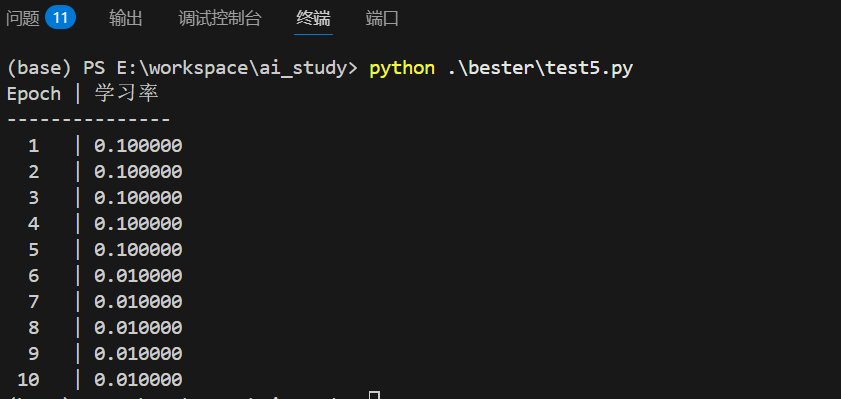
print("Epoch | 学习率")
print("-" * 15)
for epoch in range(10):
    # 此处省略实际训练步骤（前向/反向传播），仅演示学习率变化
    current_lr = optimizer.param_groups[0]['lr']
    print(f"{epoch+1:^5} | {current_lr:.6f}")
    # 调用scheduler.step()更新学习率
    optimizer.step()
    scheduler.step()

运行结果:

5.2 学习率选择实用技巧

1. 学习率探测：从小学习率开始，观察损失下降情况
2. 循环学习率：在合理范围内周期性变化学习率
3. 热重启策略：周期性重置学习率，跳出局部最优

6. 实战案例：线性回归的完整优化流程

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import torch
import torch.optim as optim
from functools import partial

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def complete_optimization_pipeline():
    """完整的优化流程示例：波士顿房价预测"""
    # 生成模拟数据
    np.random.seed(42)
    n_samples = 1000
    n_features = 5
    # 生成特征数据
    X = np.random.randn(n_samples, n_features)
    # 生成真实权重和偏置
    true_weights = np.array([2.5, -1.3, 0.8, 3.2, -0.5])
    true_bias = 1.7
    # 生成目标值（加入噪声）
    y = np.dot(X, true_weights) + true_bias + 0.1 * np.random.randn(n_samples)
    # 数据预处理
    scaler = StandardScaler()
    X_scaled = scaler.fit_transform(X)
    # 划分训练集和测试集
    X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)
    # 不同优化算法比较
    optimizers = {
        'SGD': optim.SGD,
        'Momentum': partial(optim.SGD, momentum=0.9), # 使用partial固定momentum参数
        'Adam': optim.Adam,
        'RMSprop': optim.RMSprop
    }

    results = {}
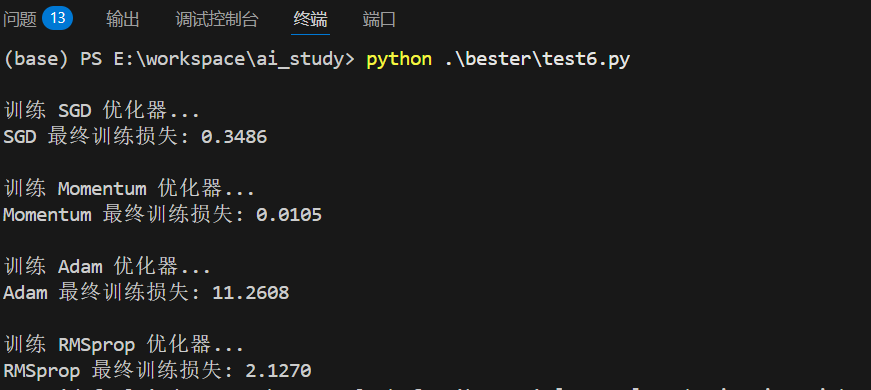
    for name, optimizer_class in optimizers.items():
        print(f"\n训练 {name} 优化器...")
        # 模型定义
        model = torch.nn.Sequential(
            torch.nn.Linear(n_features, 1)
        )
        # 定义优化器
        optimizer = optimizer_class(model.parameters(), lr=0.01)
        criterion = torch.nn.MSELoss()
        # 训练模型
        train_losses = []
        test_losses = []
        for epoch in range(100):
            # 训练阶段
            model.train()
            optimizer.zero_grad()
            # 前向传播
            outputs = model(torch.FloatTensor(X_train))
            loss = criterion(outputs, torch.FloatTensor(y_train).unsqueeze(1))
            # 反向传播
            loss.backward()
            optimizer.step()
            # 评估阶段
            model.eval()
            with torch.no_grad():
                test_outputs = model(torch.FloatTensor(X_test))
                test_loss = criterion(test_outputs, torch.FloatTensor(y_test).unsqueeze(1))
            train_losses.append(loss.item())
            test_losses.append(test_loss.item())
        results[name] = {
            'train_losses': train_losses,
            'test_losses': test_losses,
            'final_params': list(model.parameters())
        }
        print(f"{name} 最终训练损失: {train_losses[-1]:.4f}")

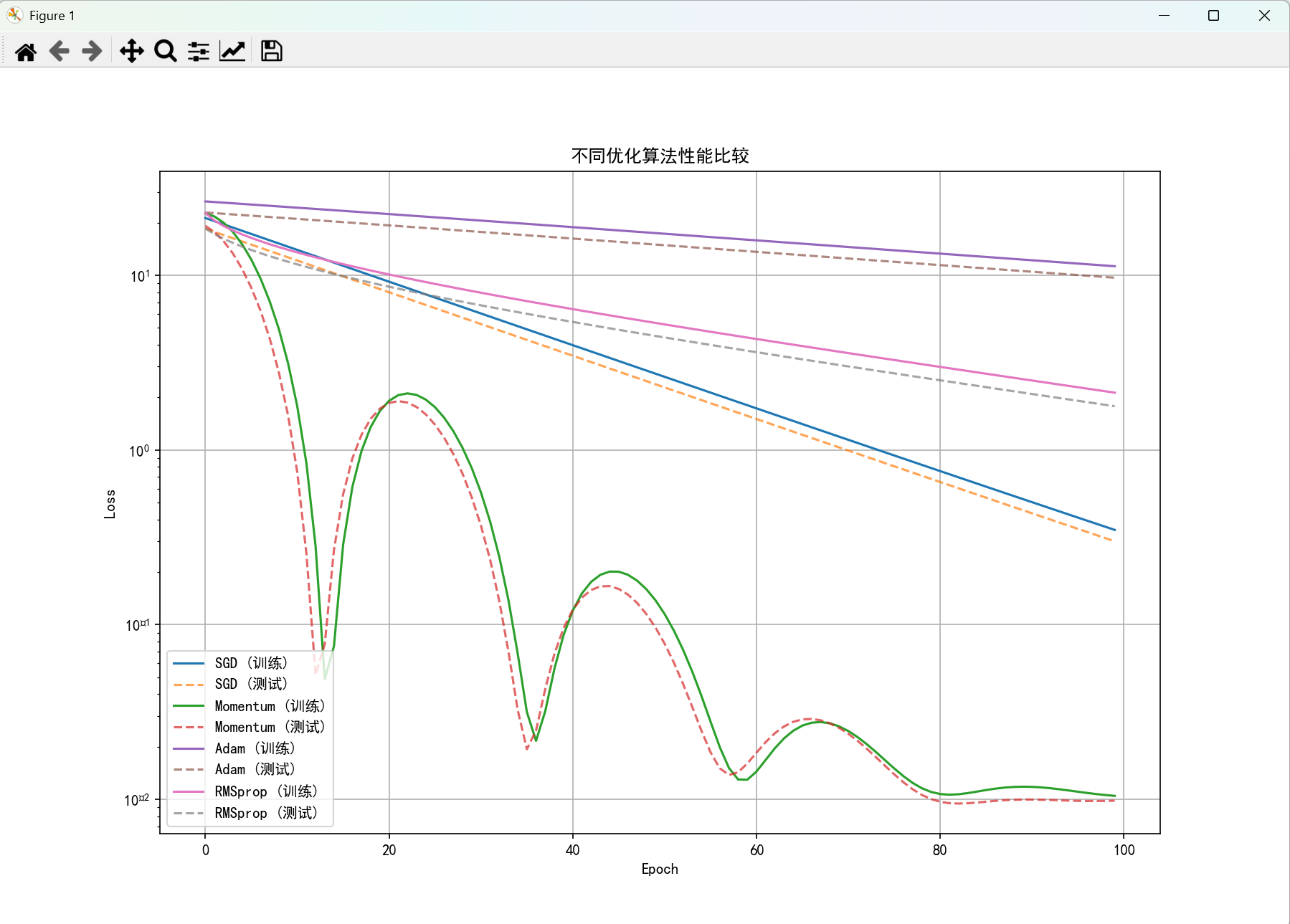
    # 可视化比较结果
    plt.figure(figsize=(12, 8))
    for name, result in results.items():
        plt.plot(result['train_losses'], label=f'{name} (训练)')
        plt.plot(result['test_losses'], '--', label=f'{name} (测试)', alpha=0.7)
    plt.xlabel('Epoch')
    plt.ylabel('Loss')
    plt.title('不同优化算法性能比较')
    plt.legend()
    plt.grid(True)
    plt.yscale('log')
    plt.show()
    return results
  
# 运行完整示例
results = complete_optimization_pipeline()

运行结果:

7. 实用技巧与故障排除

7.1 梯度裁剪：防止梯度爆炸

def gradient_clipping_example():
    """梯度裁剪示例：防止梯度爆炸"""
    
    model = torch.nn.LSTM(input_size=100, hidden_size=50, num_layers=3)
    optimizer = optim.Adam(model.parameters(), lr=0.001)
    
    # 训练循环中的梯度裁剪
    for batch_idx, (data, target) in enumerate(dataloader):
        optimizer.zero_grad()
        output = model(data)
        loss = criterion(output, target)
        loss.backward()
        
        # 梯度裁剪：限制梯度范数不超过1.0
        torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)
        
        optimizer.step()

7.2 常见问题与解决方案

问题1：损失不下降

• 原因：学习率太小、梯度消失、模型架构问题
• 解决：增大学习率、使用ReLU激活函数、检查数据流

问题2：损失震荡严重

• 原因：学习率太大、批量大小太小
• 解决：减小学习率、增大批量大小、使用动量优化器

问题3：过拟合

• 原因：模型复杂度过高、训练数据不足
• 解决：添加正则化、使用Dropout、早停策略

8. 总结与进阶学习建议

优化算法是深度学习成功的核心技术。通过本文的学习，你应该掌握：

8.1 核心要点回顾

1. 梯度下降法是基础：理解梯度方向和学习率的概念
2. 自适应算法更高效：Adam等算法适合大多数场景
3. 学习率调度很重要：动态调整学习率提升性能
4. 实践出真知：多动手实验不同算法和参数

8.2 进阶学习方向

• 二阶优化方法：牛顿法、拟牛顿法等
• 分布式优化：数据并行、模型并行策略
• 元学习优化：学习如何学习（Learning to Learn）
• 理论深度：收敛性分析、优化理论

优化算法如同深度学习的"导航系统"，掌握它，你就能在复杂的模型训练中找到最优路径。继续实践和探索，你将成为更优秀的深度学习实践者！

---

本文代码在Python 3.8+和PyTorch 1.9+环境下测试通过，建议结合实际项目进行调整和优化。欢迎在评论区交流优化算法使用经验！