文章目录
- 一、01BFS
- [二、OJ 练习](#二、OJ 练习)
-
- [1. 小明的游戏 ⭐⭐](#1. 小明的游戏 ⭐⭐)
-
- [(1) 解题思路](#(1) 解题思路)
- [(2) 代码实现](#(2) 代码实现)
- [2. Three States ⭐⭐⭐⭐](#2. Three States ⭐⭐⭐⭐)
-
- [(1) 解题思路](#(1) 解题思路)
- [(2) 代码实现](#(2) 代码实现)
上文:
一、01BFS
01BFS,可用于解决边权值只有 0 和 1 的最短路径问题。它兼具了标准 BFS 的高效性和 Dijkstra 算法处理带权图的能力。
标准 BFS 适用于所有边权都为 1 的图,它使用一个简单的 FIFO 队列,保证第一次到达某个节点时,路径就是最短的。当图的边权只有 0 和 1 时,如果使用 Dijkstra 算法显得有些大材小用,因为使用优先队列插入元素的时间复杂度为 O ( log n ) O(\operatorname{log}n) O(logn)。
但是如果我们使用一个双端队列 ,当遍历一条权值为 0 的边到达一个新节点时,我们可以直接把这个节点添加到队列的头部,反之添加到队列的尾部。这样一来,我们就达到了使用优先队列一样的效果,并且插入元素的时间复杂度就从 O ( log n ) O(\operatorname{log}n) O(logn) 降到了 O ( 1 ) O(1) O(1)。
总结一下就是:
- 正常 BFS 逻辑
- 边权为 0 -> 压入队首
- 边权为 1 -> 压入队尾
注意我们在 BFS 的时候,当第一次到达某一个位置的时候它不一定就是最短的距离。比如下面图中从 A->B 的路线中,可以发现路线 A->C->E 比路线 A->B 更短。因此我们在 BFS 遍历的时候需要判断当前距离是否比已经记录的距离更短,如果是,那么就需要更新最短距离。这个操作称为松弛操作。
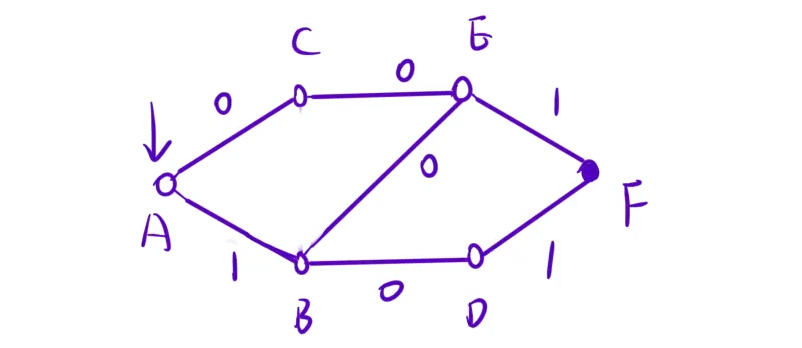
为了方便,我们可以把记录距离的 dist 数组的值初始化为无穷大,这样不管是第一次遇到某个位置还是需要松弛操作,我们都可以采用同样的逻辑,不需要额外判断。
二、OJ 练习
1. 小明的游戏 ⭐⭐
【题目链接】
【题目描述】
小明最近喜欢玩一个游戏。给定一个 n × m n \times m n×m 的棋盘,上面有两种格子
#和@。游戏的规则很简单:给定一个起始位置和一个目标位置,小明每一步能向上,下,左,右四个方向移动一格。如果移动到同一类型的格子,则费用是 0 0 0,否则费用是 1 1 1。请编程计算从起始位置移动到目标位置的最小花费。
【输入格式】
输入文件有多组数据。
输入第一行包含两个整数 n n n, m m m,分别表示棋盘的行数和列数。
输入接下来的 n n n 行,每一行有 m m m 个格子(使用
#或者@表示)。输入接下来一行有四个整数 x 1 , y 1 , x 2 , y 2 x_1, y_1, x_2, y_2 x1,y1,x2,y2,分别为起始位置和目标位置。
当输入 n n n, m m m 均为 0 0 0 时,表示输入结束。
【输出格式】
对于每组数据,输出从起始位置到目标位置的最小花费。每一组数据独占一行。
【示例一】
输入
2 2 @# #@ 0 0 1 1 2 2 @@ @# 0 1 1 0 0 0输出
2 0
【说明/提示】
对于20%的数据满足: 1 ≤ n , m ≤ 10 1 \le n, m \le 10 1≤n,m≤10。
对于40%的数据满足: 1 ≤ n , m ≤ 300 1 \le n, m \le 300 1≤n,m≤300。
对于100%的数据满足: 1 ≤ n , m ≤ 500 1 \le n, m \le 500 1≤n,m≤500。
(1) 解题思路
如果移动到同一类型的格子,相当于边权为 0,反之边权为 1,标准的 01BFS。值得注意的是,由于这道题的性质所致,此题似乎不需要松弛操作也可以过。
(2) 代码实现
cpp
#include<iostream>
#include<deque>
#include<cstring>
using namespace std;
typedef pair<int, int> PII;
const int N = 510;
char st[N][N]; // 读入棋盘
int dist[N][N]; // 记录距离
int n, m;
int x1, y1, x2, y2;
int dx[] = {0, 0, -1, 1};
int dy[] = {1, -1, 0, 0};
void bfs()
{
deque<PII> dq;
dq.push_back({x1, y1});
dist[x1][y1] = 0;
while(!dq.empty())
{
PII t = dq.front();
int r = t.first;
int c = t.second;
dq.pop_front();
for(int i = 0; i < 4; i++)
{
int rr = r + dx[i];
int cc = c + dy[i];
if(rr >= 0 && rr < n && cc >= 0 && cc < m && dist[rr][cc] == -1)
{
// 计算边权,如果类型相同则为 0,反之为 1
int w = st[r][c] == st[rr][cc] ? 0 : 1;
dist[rr][cc] = dist[r][c] + w;
// 如果边权为 0,放队头
if(w) dq.push_back({rr, cc});
// 如果边权为 1,放队尾
else dq.push_front({rr, cc});
}
}
}
}
int main()
{
while(1)
{
cin >> n >> m;
if(m == 0 && n == 0) break;
memset(dist, -1, sizeof(dist));
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j++)
cin >> st[i][j];
cin >> x1 >> y1 >> x2 >> y2;
bfs();
cout << dist[x2][y2] << endl;
}
return 0;
}2. Three States ⭐⭐⭐⭐
【题目链接】
【题目描述】
The famous global economic crisis is approaching rapidly, so the states of Berman, Berance and Bertaly formed an alliance and allowed the residents of all member states to freely pass through the territory of any of them. In addition, it was decided that a road between the states should be built to guarantee so that one could any point of any country can be reached from any point of any other State.
Since roads are always expensive, the governments of the states of the newly formed alliance asked you to help them assess the costs. To do this, you have been issued a map that can be represented as a rectangle table consisting of n rows and m columns. Any cell of the map either belongs to one of three states, or is an area where it is allowed to build a road, or is an area where the construction of the road is not allowed. A cell is called passable, if it belongs to one of the states, or the road was built in this cell. From any passable cells you can move up, down, right and left, if the cell that corresponds to the movement exists and is passable.
Your task is to construct a road inside a minimum number of cells, so that it would be possible to get from any cell of any state to any cell of any other state using only passable cells.
It is guaranteed that initially it is possible to reach any cell of any state from any cell of this state, moving only along its cells. It is also guaranteed that for any state there is at least one cell that belongs to it.
【输入格式】
The first line of the input contains the dimensions of the map n and m ( 1\<=n,m\<=1000 ) --- the number of rows and columns respectively.
Each of the next n lines contain m characters, describing the rows of the map. Digits from 1 to 3 represent the accessory to the corresponding state. The character '.' corresponds to the cell where it is allowed to build a road and the character '#' means no construction is allowed in this cell.
【输出格式】
Print a single integer --- the minimum number of cells you need to build a road inside in order to connect all the cells of all states. If such a goal is unachievable, print -1.
【题目大意】
给你一个 n ×m 的地图,
.是荒地,#是石头(不能走),数字是国家(编号为1、2、3),求最少把多少荒地修成路可以使得三个国家连通,无解输出 −1。
【示例一】
输入
4 5 11..2 #..22 #.323 .#333输出
2
【示例二】
输入
1 5 1#2#3输出
-1
(1) 解题思路
整体思路:直接找出结果点是很麻烦的,需要枚举所有的点,然后每个点都要来一次 BFS,这样是会超时的。我们可以依次从三个国家出发,用 BFS 计算出来到达所有点的最短距离。求出所有距离之后,重新遍历所有的点,分情况求出到三个国家的最短距离。
在 BFS 的过程中,如果搜索到的点是国家,那么是不需要修路就可以走的,相当于边权为 0。而如果是荒地,那么就需要修路才可以走,相当于边权为 1,可以使用 01BFS 来实现。由于一个国家可以是很多个点,所以在 01BFS 之前需要把该国家都提前加入到队列中,即多源 BFS。
在求出三个国家到每个点的最短距离之后,遍历所有的点,假设三个国家 1、2、3 到这个点的最短距离分别为 x、y、z。
- 如果这个点是荒地,那么最终需要修成路的荒地就是
x + y + z - 2,因为这个点被计算了 3 次所以要减去 2。- 如果这个点是国家 1,那么最终需要修成路的荒地就是
x + y + z,其中x为 0。- 如果这个点是国家 2 或国家 3,同理。
(2) 代码实现
cpp
#include<iostream>
#include<deque>
#include<cstring>
using namespace std;
typedef pair<int, int> PII;
const int N = 1005, INF = 0x3f3f3f3f;
int n, m;
char grid[N][N];
int dist[N][N][4];
int dx[] = {0, 0, -1, 1};
int dy[] = {1, -1, 0, 0};
// 对于某一个国家进行 BFS
void bfs(int country)
{
char t = country + 48;
deque<PII> dq;
// 多源BFS,把该国家的所有的点都先加入到队列
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
if(grid[i][j] == t)
{
dq.push_back({i, j});
dist[i][j][country] = 0;
}
}
}
// 01BFS
while(!dq.empty())
{
int x = dq.front().first;
int y = dq.front().second;
dq.pop_front();
for(int i = 0; i < 4; i++)
{
int nx = x + dx[i];
int ny = y + dy[i];
if(nx > 0 && nx <= n && ny > 0 && ny <= m && grid[nx][ny] != '#')
{
int flag = isdigit(grid[nx][ny]);
// 如果是国家,那么边权为 0,如果是荒地则为 1
int w = flag ? 0 : 1;
if(dist[nx][ny][country] > dist[x][y][country] + w)
{
dist[nx][ny][country] = dist[x][y][country] + w;
if(flag) dq.push_front({nx, ny});
else dq.push_back({nx, ny});
}
}
}
}
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
cin >> grid[i][j];
}
}
memset(dist, 0x3f, sizeof(dist));
for(int k = 1; k <= 3; k++)
{
bfs(k);
}
int res = INF;
for(int k = 1; k <= 3; k++)
{
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m ;j++)
{
if(grid[i][j] == '#') continue;
int d1 = dist[i][j][1], d2 = dist[i][j][2], d3 = dist[i][j][3];
int sum = d1 + d2 + d3;
if(sum < 0) continue; // 防止 3 个 INF 相加溢出
if(isdigit(grid[i][j])) res = min(res, sum);
else res = min(res, sum - 2);
}
}
}
if(res != INF) cout << res << endl;
else cout << -1 << endl;
return 0;
}