算法---位运算

1.位运算符号的介绍

[2. 给一个数n，确定它的二进制表示中的第x位是0还是1](#2. 给一个数n，确定它的二进制表示中的第x位是0还是1)

[3. 将一个数n的二进制表示的第x位修改成1](#3. 将一个数n的二进制表示的第x位修改成1)

[4. 将一个数n的二进制表示的第x位修改成0](#4. 将一个数n的二进制表示的第x位修改成0)

[5. 提取一个数n的二进制表示中的最右边的1](#5. 提取一个数n的二进制表示中的最右边的1)

[6. 干掉一个数n的二进制表示中的最右边的1](#6. 干掉一个数n的二进制表示中的最右边的1)

[7. 位1的个数](#7. 位1的个数)

[7.1 解题思路](#7.1 解题思路)

[7.2 代码实现](#7.2 代码实现)

[8. 比特位计数](#8. 比特位计数)

[8.1 解题思路](#8.1 解题思路)

[8.2 代码实现](#8.2 代码实现)

[9. 汉明距离](#9. 汉明距离)

[9.1 解题思路](#9.1 解题思路)

[9.2 代码实现](#9.2 代码实现)

[10. 只出现一次的数字](#10. 只出现一次的数字)

[10.1 解题思路](#10.1 解题思路)

[10.2 代码实现](#10.2 代码实现)

[11. 只出现一次的数字3](#11. 只出现一次的数字3)

[11.1 解题思路](#11.1 解题思路)

[11.2 代码实现](#11.2 代码实现)

[12. 判断字符是否为1](#12. 判断字符是否为1)

[12.1 解题思路](#12.1 解题思路)

[12.2 代码实现](#12.2 代码实现)

[13. 丢失的数字](#13. 丢失的数字)

[13.1 解题思路](#13.1 解题思路)

[13.2 代码实现](#13.2 代码实现)

[14. 两数之和](#14. 两数之和)

[14.1 解题思路](#14.1 解题思路)

[14.2 代码实现](#14.2 代码实现)

[15. 只出现一次的数字Ⅱ](#15. 只出现一次的数字Ⅱ)

[15.1 解题思路](#15.1 解题思路)

[15.2 代码实现](#15.2 代码实现)

[16. 消失的两个数字](#16. 消失的两个数字)

[16.1 解题思路](#16.1 解题思路)

[16.2 代码实现](#16.2 代码实现)

1.位运算符号的介绍

<<：左移运算符，一个数的二进制位向左移动，末尾补0。

>>：右移运算符，一个数的二进制位向右移动，这里有符号右移补符号位，无符号右移补0。

~：按位取反，就是一个数的二进制位都取反得到的数。

&：按位与，两个数按位与，二进制位进行比较，有0则为0。

|：按位或，两个数按位或，二进制位进行比较，有1则为1。

^：按位异或，两个数按位异或，二进制位进行比较，相同为0，不同为1。

异或的相关运算规则：

a ^ 0 = a a ^ a = 0 a ^ b ^ c = a ^ ( b ^ c)

注意：这里我们在使用不同的位运算符的时候，我们要根据运算的优先级加小括号。

2. 给一个数n，确定它的二进制表示中的第x位是0还是1

这道题是给我们一个数n，让我们求该数的二进制表示位，从右往左数第x位是0还是1。

这道题我们可以把这个数n >> x 次，此时我们判断的位数就在最后一位，此时我们再让这个数&1，这时候得到的数为0，则x位为0，得到的数为1，则x位为1。

(n >> x) & 1

3. 将一个数n的二进制表示的第x位修改成1

这道题让我们把数n的二进制表示的从右往左数第x位修改成1。

这道题我们可以先让1 << x 位，然后让这个数 | n ，最后得到结果，此时其他位置的数都是 | 0，这个数还是保持不变。

n = n | (1 << x)

4. 将一个数n的二进制表示的第x位修改成0

这道题让我们把数n的二进制表示的从右往左数第x位修改成0。

这道题我们可以先让1 << x 位，然后，让这个数再按位取反，将这个数 & n ，最后就是正确结果。

( ~(1 << x ) ) & n

5. 提取一个数n的二进制表示中的最右边的1

这道题让我们把一个数n的二进制表示中的最右边的一个1提取出来，最后返回该位置为1，其他位置为0的数。

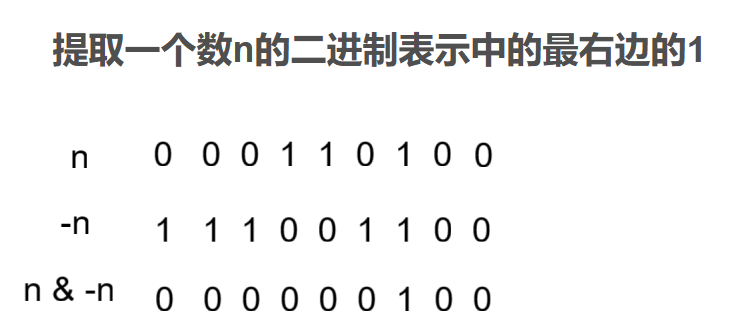
这里我们会发现将一个数n 得到的相反数 -n,这个相反数最后一个1位置的左边的数跟n对应位置数取反，右边的数跟n对应位置的数相同。此时我们就可以让这两个数按位&，得到最后结果。

n & (-n)

6. 干掉一个数n的二进制表示中的最右边的1

这道题让我们把一个数n位置的二进制表示中的最右边的1删除，也就是将该位置的1变为0。

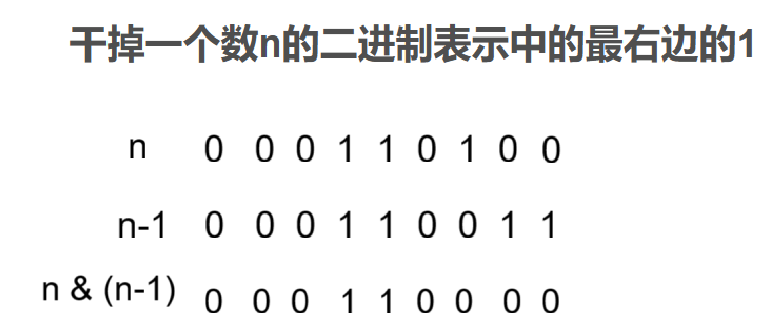
这里我们发现将n-1后得到的数的二进制表示的数，最右边1位置的左边跟n对应位置数相同，右边跟n对应位置数相反。此时让这两个数按位与，就能得到最后结果。

n & (n-1)

7. 位1的个数

题目链接

7.1 解题思路

这道题给我们一个数n，让我们求该数的二进制表示形式中的1的个数。

7.2 代码实现

java 复制代码

class Solution {
    public int hammingWeight(int n) {
        int count = 0;
        while(n != 0) {
            if((n & 1) != 0) {
                count++;
            }
            n = n >> 1;
        }
        return count;
    }
}

8. 比特位计数

题目链接

8.1 解题思路

这道题给我们一个数n，让我们求0~n的所有数的二进制表示形式分别有多少1，然后放到一个大小为n+1的数组里面，返回这个数组。

我们采用暴力解法，直接遍历每个数，将每个数的1个数求出来放到数组里面。这种方法的时间复杂度为O（nlogn）。

我们可以采用优化的方法，我们前面介绍了一个数如何消灭最右边的1，消灭1后的数比原来数小，这时候，我们就能想到求一个数的二进制1的个数，转换为求这个数消灭最右边1的数再+1。

这时候需要初始0为0的1。这个方法时间复杂度为O（n)。

8.2 代码实现

java 复制代码

class Solution {
    public int[] countBits(int n) {
        int[] ans = new int[n+1];
        if(n < 0) {
            return null;
        }
        ans[0] = 0;
        for(int i = 1; i <= n; i++) {
            ans[i] = ans[i & (i-1)] + 1;
        }
        return ans;
    }
}

9. 汉明距离

题目链接

9.1 解题思路

这道题给我们两个数字，让我们求这两个数字的二进制表示对应的位数不同的个数。

这里我们会想到使用^运算符，不同为1，先将两个数异或，然后得到的数里面有几个1就是最后结果。

9.2 代码实现

java 复制代码

class Solution {
    public int hammingDistance(int x, int y) {
        int z = x ^ y;
        int count = 0;
        while(z > 0) {
            if((z & 1) == 1) {
                count++;
            }
            z = z >> 1;
        }
        return count;
    }
}

10. 只出现一次的数字

题目链接

10.1 解题思路

这道题给我们一个非空数组，其中只有一个元素出现一次，其他元素出现两次。

这里我们可以用异或的运算律，a ^ a = 0 a ^ 0 = a，将数组里面元素全部异或，最后剩下的数就是最后结果。

10.2 代码实现

java 复制代码

class Solution {
    public int singleNumber(int[] nums) {
        int tmp = nums[0];
        for(int i = 1; i < nums.length; i++) {
            tmp ^= nums[i];
        }
        return tmp;
    }
}

11. 只出现一次的数字3

题目链接

11.1 解题思路

这道题给我们一个数组，里面包含两个不同的单独的数，其他数全是两个，让我们返回由这两个单独的数组成的数组。

我们可以采用暴力解法，利用哈希表遍历数组，然后找到哈希表中数为1的数，返回。

我们还可以使用位运算，将数组里面所有数相互异或，最后得到的数是两个不同的数x1和x2异或后的数x，然后我们提取x里面最右边的1得到数n，然后我们将数组里面的数与这个数按位与运算得到的数可以分为两类，一类该位置是0，一类该位置是1，而这两个单独的数x1和x2也在不同类中，我们就遍历这个数组元素分别&n，将结果分类，最后得到两个数就是最后结果。

这里我们还需要考虑数据溢出问题，如果x 是整型Int最小的值 -2147483648 ，在提取最右边1的数时取相反数为2147483648,这里就会发生溢出，此时最小值的提取最右边1的数就是它本身。

11.2 代码实现

java 复制代码

class Solution {
    public int[] singleNumber(int[] nums) {
        int x = 0;
        for(int tmp : nums) {
            x ^= tmp;
        }
        //此时x是两个数异或的结果
        //提取出该数的最右边的1，防止溢出
        int right = (x == Integer.MIN_VALUE ? x : x & (-x));
        int x1 = 0, x2 = 0;
        for(int tmp : nums) {
            //tmp对应位置为0
            if((tmp & right) == 0) {
                x1 ^= tmp;
            }else {
                x2 ^= tmp;
            }
        }
        return new int[]{x1,x2};
    }
}

12. 判断字符是否为1

题目链接

12.1 解题思路

这道题给我们一个字符串s，s全是小写字母，让我们判断字符串中的字符是否都不相同，也就是没有重复的字符。

我们可以采用暴力解法，遍历字符串一遍，将字符和出现的次数存到哈希表里面。

我们还可以使用位运算，一个int类型的数据有32个比特位，我们可以从右往左，从0开始表示a到z的字符，我们这里利用上面的结论，遍历字符串，判断该字符对应比特位是否为1，0表示该字符没出现过，1表示该字符出现过，当对应比特位为1时候就返回false，当对应比特位为0时候就将该比特位改成1。

这里还可以优化，当字符串的长度大于26时候，一定会返回false。

12.2 代码实现

java 复制代码

class Solution {
    public boolean isUnique(String astr) {
        char[] arr = astr.toCharArray();
        if(arr.length > 26) {
            return false;
        }
        int n = 0;
        for(char x : arr) {
            int tmp = x - 'a';
            if(((n >> tmp) & 1) == 1) {
                return false;
            }else {
                n = (n | (1 << tmp));
            }
        }
        return true;
    }
}

13. 丢失的数字

题目链接

13.1 解题思路

这道题给我们一个数组，里面包含0~n之间的n个数，说明数组里面缺少一个数在0~n之间。返回这个数。

这道题有多种解法：

我们可以使用高斯求和公式，求出0~n的和，然后减去原数组所有元素，最后得到的数就是最后结果。

我们还可以使用异或运算符，将0~n的数和数组里面所有数都进行异或运算，最后的结果就是最终答案。

13.2 代码实现

java 复制代码

class Solution {
    public int missingNumber(int[] nums) {
        int len = nums.length;
        int tmp = 0;
        for(int i = 0; i < len; i++) {
            tmp = tmp ^ nums[i] ^ i;
        }
        tmp ^= len;
        return tmp;
    }
}

14. 两数之和

题目链接

14.1 解题思路

这道题给我们两个整数a和b，让我们不用+和-求和，那我们肯定要采用位运算来解决。

我们会想到异或的性质，无进位求和，也就是说两个数异或，两个数对应位置的二进制位，求和后不会进位，符合&的性质，我们就可以每次让两个数异或，然后加上进位的数，这里我们进位的数应该左移一位的，再进行相加，直到进位的数为0位置。此时两个数异或的结果就是最后答案。

14.2 代码实现

java 复制代码

class Solution {
    public int getSum(int a, int b) {
        while(b != 0) {
            int sum = a ^ b;
            int tmp = (a & b) << 1;//进位
            a = sum;
            b = tmp;
        }
        return a;
    }
}

15. 只出现一次的数字Ⅱ

题目链接

15.1 解题思路

这道题给我们一个数组，数组里面除了一个数只出现一次外，其他的数都出现三次，让我们找到只出现一次的那个数。

我们首先想到的是哈希表，将每个数字出现的次数放到哈希表里面。

我们也可以利用位运算算法，从右往左计算所有数的每个比特位的和然后取余3，计算出来的比特位就是目标值的比特位，我们循环上面依次计算每位比特位。

15.2 代码实现

java 复制代码

class Solution {
    public int singleNumber(int[] nums) {
        int tmp = 0;
        for(int i = 0; i < 32; i++) {
            int sum = 0;
            for(int x : nums) {
                //判断第i位的数是否为1
                if(((x >> i) & 1) == 1) {
                    sum += 1;
                }
            }
            sum %= 3;
            if(sum == 1) {
                //将第i位的数修改成1
                tmp = (tmp | (1 << i));
            }
        }
        return tmp;
    }
}

16. 消失的两个数字

16.1 解题思路

这道题给我们一个数组包含0~n的所有整数，但是缺少两个，让我们返回缺少的这两个数。

我们可以将数组里面的所有数和 1~n所有的数之间异或起来得到最后结果tmp是两个缺失的数的异或的结果。

然后我们提取出tmp里面最右边的1的数n，然后我们将数组里面所有数和1~n所有的数分为两组，一组是& n等于0的数，另一组是 & n 不等于0的数。

16.2 代码实现

java 复制代码

class Solution {
    public int[] missingTwo(int[] nums) {
        //数组里面的数和1~n之间的数全部异或得到两个单独的数的异或结果
        int len = nums.length;
        int tmp = nums[0];
        for(int i = 1; i < len; i++) {
            tmp = tmp ^ nums[i] ^ i;
        }
        tmp = tmp ^ len ^ (len + 1) ^ (len + 2);
        //提取最右边的1(防止溢出)
        int right = tmp == Integer.MIN_VALUE ? tmp : tmp & (-tmp);
        int num1 = 0, num2 = 0;
        for(int i = 0; i < len; i++) {
            if((nums[i] & right) != 0) {
                num1 ^= nums[i];
            }else {
                num2 ^= nums[i];
            }
        }
        for(int i = 1; i <= len+2; i++) {
            if((i & right) != 0) {
                num1 ^= i;
            }else {
                num2 ^= i;
            }
        }
        return new int[]{num1,num2};
    }
}