31.下一个排列

参考讲解视频：这个排列有点难嗷！｜31. 下一个排列｜回溯｜算法｜数据结构｜编程｜程序员｜前端开发｜java面试｜华为认证｜C++_哔哩哔哩_bilibili

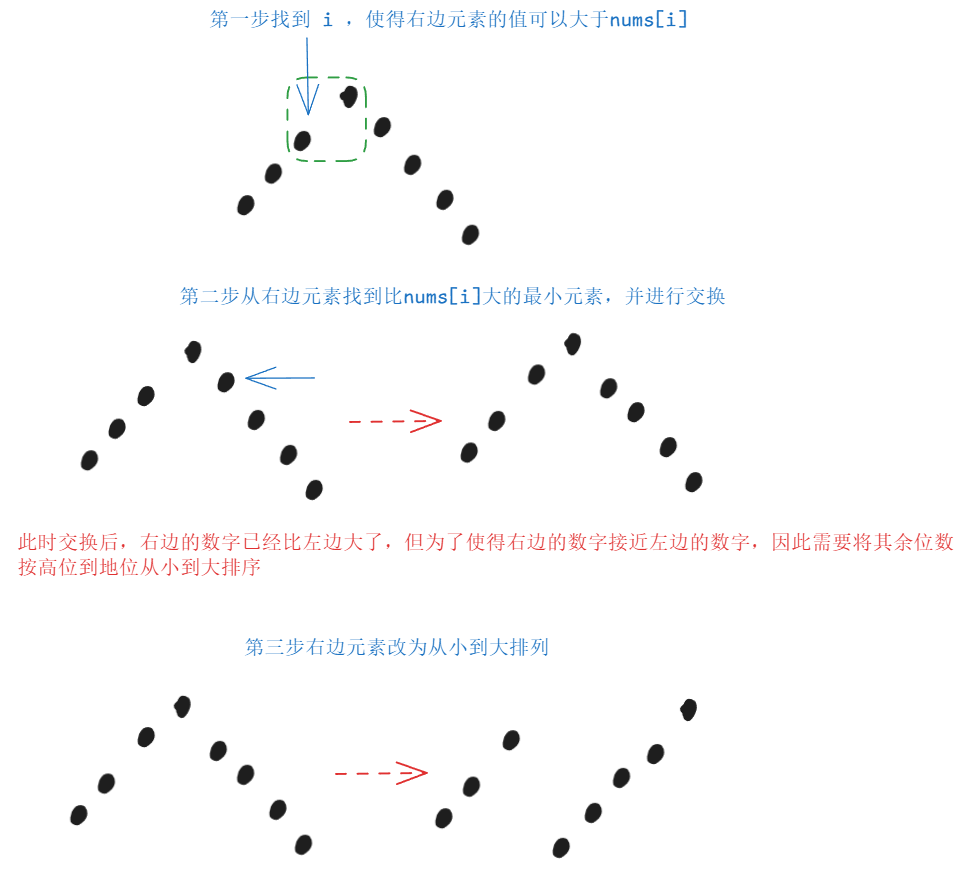
思路：

优化实现：

已遍历得到的元素我不用通过一个candidate去进行保存，这些元素还是保存在数组中，我后续要用到的时候，只需要从swap_index的右边去进行查找来得到比大于nums $swap_index$ 下的最小数字

手撕Code

python 复制代码

class Solution:
    def nextPermutation(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        
        n = len(nums)
        
        i = n - 2

        ### 第一步
            ## 逆序遍历，找到单调递减 nums[i+1] > nums[i] 的部分，此时表明了nums[i]这个元素可以被右边更大的元素所替代
            ## 当nums[i+1] > nums[i] 时，此时循环就终止了

        while i >= 0 and nums[i] >= nums[i+1]:      
            i -= 1
        
        ### 第二步
            ## 第一步已经保证了 [i+1:]的元素都是单调递减的了，此时我们要从这些元素中找到一个比nums[i]大的最小元素，去替换掉nums[i]
            ## 第一步跳出循环的方式有两种，一种是找到了nums[i+1] > nums[i] 的部分，一种是 i = -1; 后者则表示整个数组都是单调递减的，此时已经是最大的一个数字了。
            ## 即最后一个排列
        if i >= 0:
            for j in range(i+1, len(nums)):
                if nums[j] > nums[i]:
                    swap_index = j
            
            nums[i], nums[swap_index] = nums[swap_index], nums[i]


        ### 第三步，反转之后的部分
        left, right = i+1, len(nums)-1      ## 后续元素从单调递减改为单调递增，这样元素才会更小
        while left < right:
            nums[left], nums[right] = nums[right], nums[left]
            left += 1
            right -= 1

Code

python 复制代码

class Solution:
    def nextPermutation(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        
        n = len(nums)

        i = n - 2       

        ## 第一步，找到nums[i+1] > nums[i]时 i 的位置
        while i >= 0 and nums[i] >= nums[i+1]:
            i -= 1
        
        ## 第二步，找到大于nums[i]的最小元素
        if i >= 0:              ## 如果 i < 0, 那就表示整个数组都是单调递减的，当前这个数字是最大的
            j = n - 1
            while j >= i+1:
                if nums[j] > nums[i]:       ### 找到了大于nums[i]的最小元素
                    nums[i], nums[j] = nums[j], nums[i]
                    break
                
                j -= 1

       ### 反转实现1 
        # left, right = i+1, len(nums)-1
        # while left < right:
        #     nums[left], nums[right] = nums[right], nums[left]
        #     left += 1
        #     right -= 1
        
       ### 反转实现2
        # nums[i+1:] = nums[i+1:][::-1]
    
       ### 反转实现3
        nums[i+1:] = reversed(nums[i+1:])