系列文章目录
上一篇文章：【C++闯关笔记】STL：stack与queue的学习和使用-CSDN博客
下一篇文章：【C++闯关笔记】模板的特化-CSDN博客
文章目录
目录
[①AdjustUP( )向上调整算法](#①AdjustUP( )向上调整算法)
[②AdjustDown(size_t pos)向下调整算法](#②AdjustDown(size_t pos)向下调整算法)
前言
仔细观察下图，库中stack与queue的实现，似乎并不是用的vector和list实现的，而是都使用了同一种容器------deque作为底层？那么你是否了解deque的原理呢？
dequeue与priority_queue这两种容器，在一些教材中都不会怎么提及，但在实际编码过程中却可能会使用它们。
本文主要介绍deque的使用，以及priority_queue的使用和模拟实现。
一、deque是什么？
1.容器适配器
先看定义：
适配器是一种设计模式，该种模式是将一个类的接口转换成客户希望的另外一个接口。
在日常生活中，我们就经常用到电源适配器，比如手机充电器、电脑电源适配器等，它们将墙上的电源插口转换为我们希望使用的接口。
在说回C++，虽然stack和queue中也可以存放元素，但在STL中并没有将其划分在容器的行列，而是将其称为 容器适配器 ，这是因为stack和队列只是对其他容器的接口进行了包装，STL中stack和queue默认使用deque。
2.deque的介绍
定义
deque：一种双开口的"连续"空间的数据结构，一般称它为双端队列。
解释
①什么是"双开口"？
双开口的含义是：可以在头尾两端进行插入和删除操作，且时间复杂度为O(1)。与vector比较，deque头插效率高，不需要搬移元素；与 list 比较，空间利用率比较高。
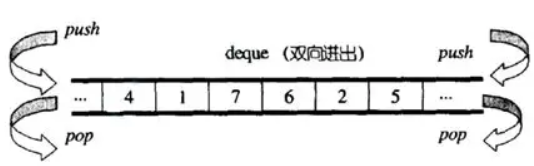
②"连续"为什么加引号？
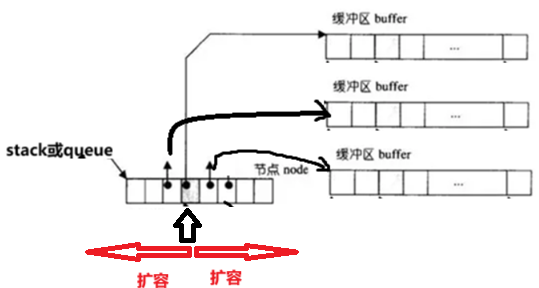
因为deque并不是真正连续的空间，而是由一段段连续的小空间拼接而成的。 实际deque类似于一个动态的二维数组，先是一个数组存储节点node，然后每一个node节点又存储着指向另一个buffer数组的指针。其底层结构如下图所示：
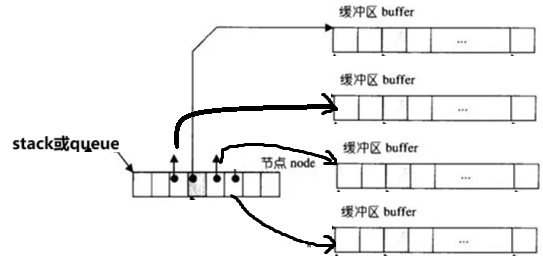
双端队列底层是一段假象的连续空间，实际是分段连续的，为了维护其"整体连续"以及随机访问 的假象，落在了deque的迭代器身上，因此deque的迭代器设计就比较复杂，如下图所示：
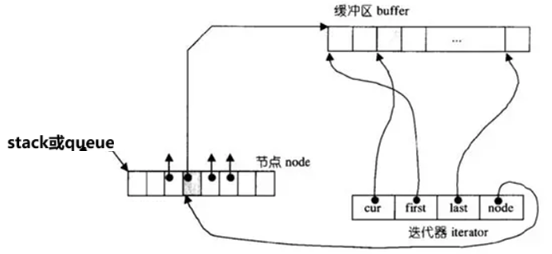
3.deque的使用
使用deque需要包含头文件#include<deque>。 deque的实际存储结构非常复杂，**但他的使用与其他容器则没什么区别。**经常使用的函数包括：
以及重载的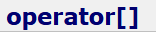
函数：支持像普通数组或者vector那样通过下标访问。
这些函数大部分都是在其他容器中出现过，相关使用这里就不再赘述，有区别的地方仅在于insert与erase是配合迭代器使用的，如下代码所示。
cpp
#include<iostream>
#include<deque>
using namespace std;
void test()
{
deque<int> d;
d.insert(d.begin(), 3);
d.insert(d.begin(), 2);
d.insert(d.begin(), 1);
for (auto& x : d)cout << x << ' ';
cout << endl;
d.erase(d.begin() + 1);
for (auto& x : d)cout << x << ' ';
cout << endl;
}
int main()
{
test();
return 0;
}
4.deque的致命缺陷
①为什么选择deque作为stack与queue的底层实现？
stack是一种后进先出的特殊线性数据结构，因此只要具有push_back()和pop_back()操作的线性结构，都可以作为stack的底层容器，比如vector和list都可以；
queue是先进先出的特殊线性数据 结构，只要具有push_back和pop_front操作的线性结构，都可以作为queue的底层容器，比如 list。
但是STL中对stack和queue默认选择deque作为其底层容器，主要是因为：
与vector比较，deque的优势是：头部插入和删除时，不需要搬移元素，效率特别高，而且在扩容时，也不需要搬移大量的元素 (扩容时不需要搬移大量数据，只需要再开一个node存储即可)，所以其效率是肯定比vector高的。 与list比较，其底层是连续空间，空间利用率比较高，不需要存储额外字段。
②deque的致命缺陷
deque有一个致命缺陷：不适合遍历。
因为deque是从中间开始存储的，增/删节点都通过申请/释放一个一段连续的空间。
在遍历时，deque的迭代器要频繁的去检测是否移动到某段小空间的边界，导致效率低下，而一些场景中，可能需要经常遍历，因此在实际中，需要线性结构时，大多数情况下优先考虑vector和list，deque的应用并不多，而其中一个应用就是STL用其作为stack和queue的底层数据结构。
二、priority_queue的学习和模拟实现
1.老熟人priority_queue？
如果你看过我之前的一期博客：【数据结构】二叉树①-堆-CSDN博客，就会发现其实priority_queue优先级队列本质上就是用动态数组实现的堆式二叉树。
先看定义
priority_queue优先级队列是一种容器适配器 ，**根据严格的排序标准，它的第一个元素总是它所包含的元素中最大的/最小的。**它的上下文类似于堆，在堆中可以随时插入元素并能保持自身结构不变，并且在检索时只能检索最大堆元素(优先队列中位于顶部的元素)。
优先级队列默认使用vector作为其底层存储数据的容器， 在vector上又使用了堆算法将vector中元素构造成堆的结构，因此priority_queue就是堆，所有需要用到堆的位置，都可以考虑使用 priority_queue。
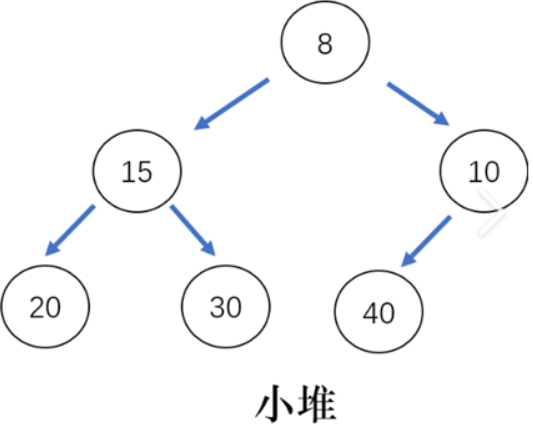
考虑到堆的概念性内容涉及二叉树，这里直接给出堆逻辑结构与物理结构的对照图。
对前因后果感兴趣的读者可点击【数据结构】二叉树①-堆-CSDN博客蓝字跳转学习， 只要理解了下图中堆**逻辑结构与物理结构的关系，**对本文足矣。
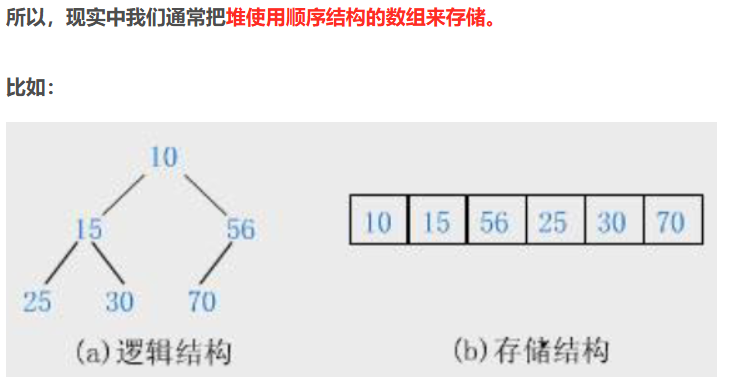
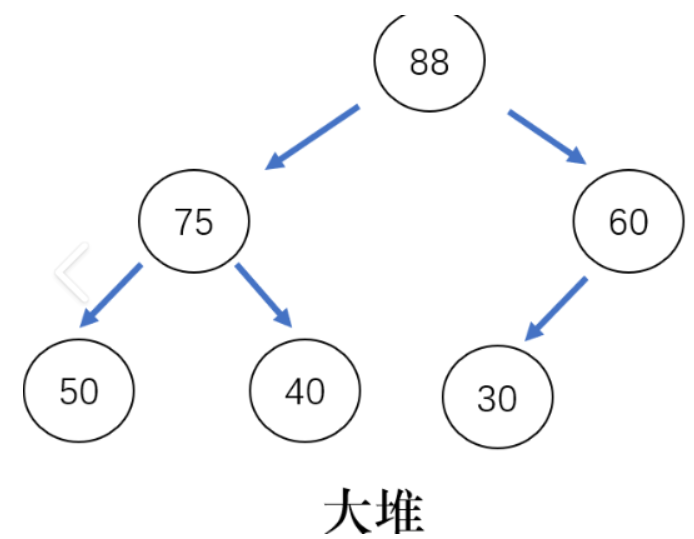
大堆：父必须大于等于子。
小堆：父必须小于等于子。
2.priority_queue的使用
使用priority_queue需要包含头文件#include<queue>，在默认情况下priority_queue是大堆。
priority_queue提供的接口较少，且大多都与其他容器的接口用法类似，在日常使用中常用到如下接口。
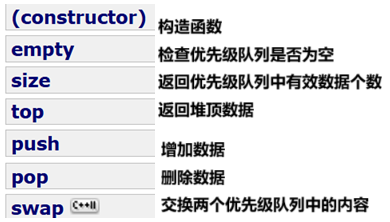
代码示例
cpp
#include<iostream>
#include<queue>
using namespace std;
void test_priority_queue()
{
priority_queue<int> p;
p.push(75);
p.push(60);
p.push(88);
p.push(50);
p.push(30);
p.push(20);
cout << "size():" << p.size() << endl;
while (!p.empty())
{
cout << p.top() << ' ';
p.pop();
}
}
int main()
{
test_priority_queue();
return 0;
}
3.模拟实现priority_queue
priority_queue的底层容器可以是其他类型的容器（如deque）------只需要满足可以通过随机访问迭代器访问，并支持以下操作即可：
本文依旧使用vector为底层模拟实现priority_queue，首先介绍仿函数是什么。
仿函数
如果一个类没有成员变量，且成员函数只重载了operator( )，那么该种类就被称为仿函数。
如：
cpp
template<class T>
class Less
{
public:
bool operator()(const T& a,const T& b)
{
return a < b;
}
};在使用该类时，通过定义一个对象然后调用( )即可。由于类似于函数调用，故又被称为仿函数。
cpp
Less l;
//l(2,3) == l.operator()(2, 3)
l(2, 3);为什么介绍仿函数呢？
因为priority_queue中的大/小堆的区别就是使用不同的仿函数。
有了仿函数的基础就可以实现priority_queue了**，**以下为priority_queue的模拟实现，这里实现的是大堆，小堆类似：
模拟实现代码
cpp
#pragma once
#include<vector>
namespace karsen
{
template<class T>
class Less
{
public:
bool operator()(const T& a,const T& b)
{
return a < b;
}
};
template<class T,class Container = vector<T>,class Compare = Less<T>>
class priority_queue
{
public:
void push(const T& val)
{
_con.push_back(val);
AdjustUP();
}
void AdjustUP()
{
size_t child = _con.size() - 1;
size_t parent = (child - 1) / 2;
Compare com;
//大堆用小于，小堆用大于
//while (parent >= 0 && Compare(parent, child))
while (child>0)
{
//如果父节点小于子节点，交换
if (com(_con[parent], _con[child]))
{
std::swap(_con[parent], _con[child]);
child = parent;
parent = (child - 1) / 2;
}
else
{
//这里默认除去新插入的，其余均为排好的堆；
//从0开始插入，自然是排好的
break;
}
}
}
void pop()
{
if (_con.empty())return;
//将最小的与最大的交换，pop之后若还有数据就调用向下调整算法
std::swap(_con.front(), _con.back());
_con.pop_back();
if (!_con.empty())AdjustDown(0);
}
void AdjustDown(size_t pos)
{
size_t parent = pos;
size_t child = parent * 2 + 1;
size_t n = _con.size();
Compare com;
while (child<n)
{
//这里有一个隐含的问题：我们可能只有一个孩子（即左孩子存在，右孩子不存在）。
//在这种情况下，代码会访问_con[rchild]，即越界访问。
//size_t min_child = _con[lchild] < _con[rchild] ? lchild : rchild;
//选大的上去，建大根堆
if (child + 1 < n && com(_con[child],_con[child + 1]))child += 1;
if (com(_con[parent], _con[child]))
{
std::swap(_con[parent], _con[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//如果直接删front(),那么堆的结构会被破坏，无法再通过AdjustDown调整
//void pop()
//{
// _con.pop_front();
// AdjustDown();
//}
const T& top()const
{
return _con.front();
}
size_t size()
{
return _con.size();
}
bool empty()
{
return _con.empty();
}
void swap(priority_queue& p)
{
std::swap(_con, p._con);
}
private:
Container _con;
};
}为了保持堆的结构 ，在Push或者Pop数据后，需要通过两种算法AdjustUP( )向上调整算法与AdjustDown(size_t pos)向下调整算法调动数据。
解释
①AdjustUP( )向上调整算法
核心思路
①默认数组第一个元素为根节点数据；
②之后每Push进一个数据，便与它的父节点比较，若父节点数据大于子节点数据，则交换，然后将父节点(下标)赋值给子节点，再计算新父节点，重复上述步骤，直至子节点到根结点处（下标为0时）。
③中途若父节点数据小于等于子节点数据（满足小堆要求），则break跳出循环。
计算新父节点： （左孩子或者右孩子的下标-1）/ 2就==他们父节点的下标，比如数组下标1与数组下标2的父节点在数组中就是下标0；
每push进一个数据，先让他做当前位置对应的左或者右孩子，然后通过向上调整算法，若数据大于父节点中的数据，则交换、上升直到第一个数据。
②AdjustDown(size_t pos)向下调整算法
核心思路
①选择该父节点对应的左/右孩子节中值较小的那一个，与父节点的值交换（一开始是根节点，即下标0处数据）；
②将交换的孩子节点当作新一轮的父节点，重复①；
③直到数组末尾，或者中途遇到大于或等于，满足小堆条件退出。
新父节点下标：已知父节点的数组下标，那么该节点的左孩子数组下标=父节点下标*2+1，右孩子数组下标=（父节点下标+1）*2。如父节点数组下标为0，则左孩子为0*2+1，右孩子为（0+1)*2。
总结
本文介绍了C++ STL中的deque和priority_queue两种容器或适配器。
首先介绍了什么是容器适配器，介绍deque的使用方法，之后注重介绍了为什么stack与queue选择deque做底层以及deque的致命缺陷；
然后介绍了优先级队列riority_queue的本质就是数据结构 堆，之后介绍了它的使用以及什么是仿函数，最后通过模拟实现的代码着重介绍了两种堆算法。
读完点赞，手留余香~