
C++专栏:C++_Yupureki的博客-CSDN博客
目录
[1. 二叉搜索树的基本概念](#1. 二叉搜索树的基本概念)
[1.1 什么是二叉搜索树?](#1.1 什么是二叉搜索树?)
[1.2 ⼆叉搜索树的性能分析](#1.2 ⼆叉搜索树的性能分析)
[2. 二叉搜索树的基本操作](#2. 二叉搜索树的基本操作)
[2.1 查找操作](#2.1 查找操作)
[2.2 插入操作](#2.2 插入操作)
[2.3 删除操作](#2.3 删除操作)
[4. 二叉搜索树key和key/value使用场景](#4. 二叉搜索树key和key/value使用场景)
[4.1 key搜索场景:](#4.1 key搜索场景:)
[4.2 key/value搜索场景](#4.2 key/value搜索场景)
[5. 二叉搜索树的性能分析与优化](#5. 二叉搜索树的性能分析与优化)
[5.1 时间复杂度分析](#5.1 时间复杂度分析)
[5.2 二叉搜索树的局限性](#5.2 二叉搜索树的局限性)
[5.3 解决方案:平衡二叉搜索树](#5.3 解决方案:平衡二叉搜索树)
上一篇:从零开始的C++学习生活 10:继承和多态-CSDN博客
前言
在计算机科学中,高效的数据搜索是许多应用的核心需求。
一般的STL如string,vector和list的查找数据的时间复杂度都是O(N),这对于大量的数据检索是完全不够的
二叉搜索树(Binary Search Tree, BST)作为一种基础而重要的数据结构,以其独特的性质在搜索、插入和删除操作中展现出优异的性能。它不仅是理解更复杂树结构(如AVL树、红黑树)的基础,更是许多实际应用场景中的首选解决方案。
我将深入探讨二叉搜索树的原理、实现和应用,帮助你全面掌握这一重要数据结构,为学习更高级的树形结构打下坚实基础。

1. 二叉搜索树的基本概念
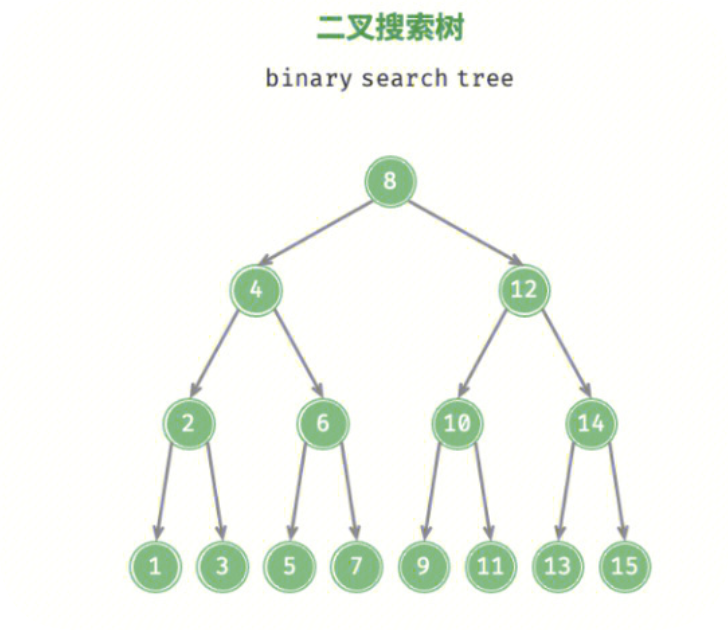
1.1 什么是二叉搜索树?
二叉搜索树(Binary Search Tree)是一种特殊的二叉树,它具有以下性质:
-
若左子树不为空,则左子树上所有节点的值都小于等于根节点的值
-
若右子树不为空,则右子树上所有节点的值都大于等于根节点的值
-
左右子树也都是二叉搜索树
这种有序性使得我们能够高效地进行查找、插入和删除操作。
1.2 ⼆叉搜索树的性能分析
最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其高度为: log2 N 最差情况下,二叉搜索树退化为单支树(或者类似单支),其高度为: N 所以综合而言二叉搜索树增删查改时间复杂度为: O(N)
另外需要说明的是,二分查找也可以实现级别的查找效率,但是二分查找有两大缺陷:
-
需要存储在支持下标随机访问的结构中,并且有序。
-
插入和删除数据效率很低,因为存储在下标随机访问的结构中,插入和删除数据⼀般需要挪动数 据。
这里也就体现出了平衡二叉搜索树的价值。
-
动态性能:支持高效的动态插入和删除
-
有序存储:数据自然有序,便于范围查询
-
灵活扩展:可以轻松扩展为更复杂的平衡树结构
2. 二叉搜索树的基本操作
2.1 查找操作
查找是二叉搜索树最基本的操作
-
从根开始比较,查找x,x比根的值大则往右边走查找,x比根值小则往左边走查找
-
最多查找高度次,走到到空,还没找到,这个值不存在
-
如果不支持插入相等的值,找到x即可返回
-
如果支持插入相等的值,意味着有多个x存在,一般要求查找中序的第一个x
cpp
bool Find(const K& key) {
Node* cur = _root;
while (cur) {
if (cur->_key < key) {
cur = cur->_right; // 在右子树中查找
} else if (cur->_key > key) {
cur = cur->_left; // 在左子树中查找
} else {
return true; // 找到目标
}
}
return false; // 未找到
}cur有两种情况:
-
没有找到,cur为空指针->退出循环,返回false
-
找到了,返回true
时间复杂度:
-
最好情况:O(log n) - 树完全平衡时
-
最坏情况:O(n) - 树退化为链表时
2.2 插入操作
插入操作需要保持二叉搜索树的性质:
-
若左子树不为空,则左子树上所有节点的值都小于等于根节点的值
-
若右子树不为空,则右子树上所有节点的值都大于等于根节点的值
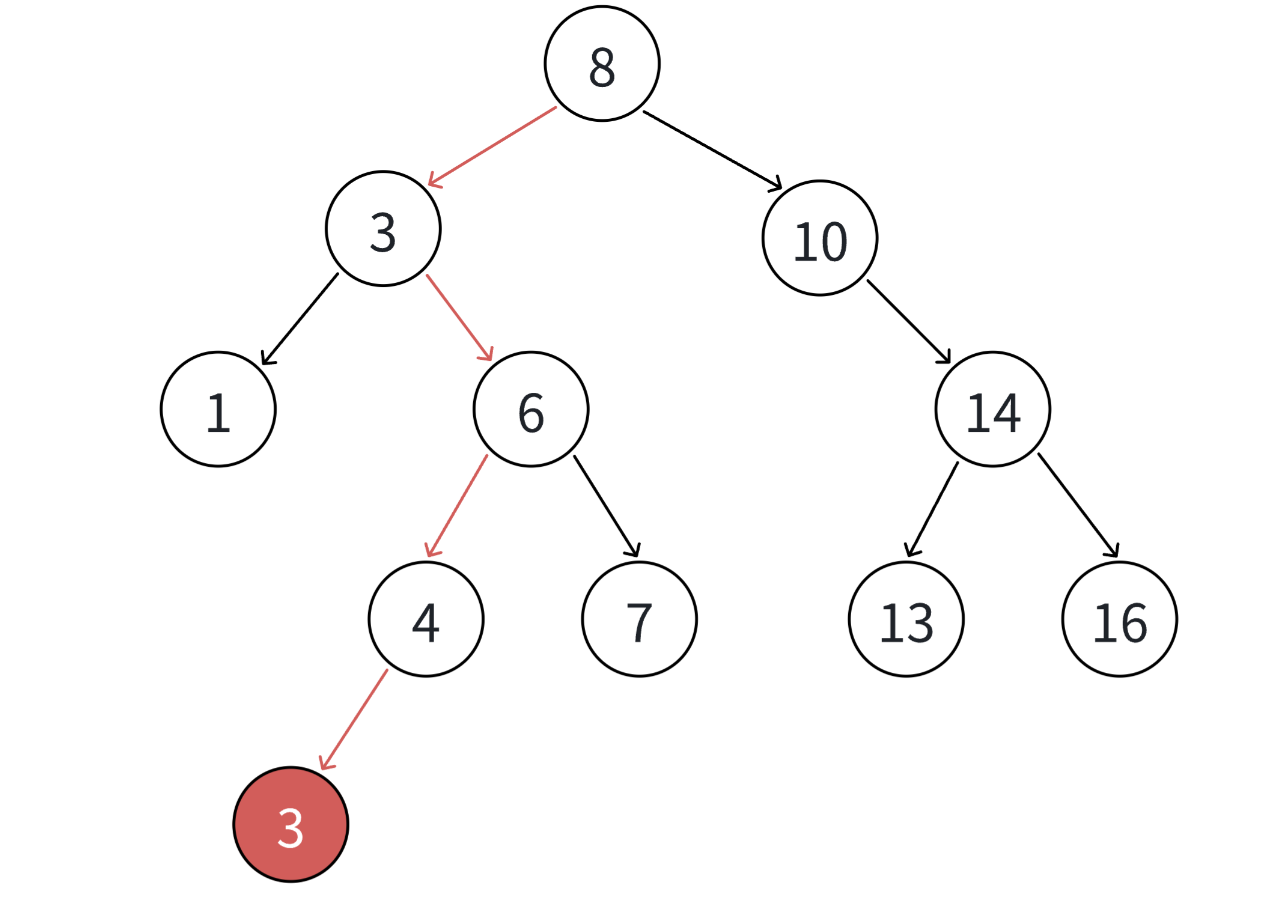
因此我们分以下情况:
- 树为空,即根节点都不存在,那么直接把插入的节点当作根节点
- 树不空,按二叉搜索树性质,插入值比当前结点大往右走,插入值比当前结点小往左走,找到空位置,插入新结点。
- 如果支持插入相等的值,插入值跟当前结点相等的值可以往右走,也可以往左走,找到空位置,插入新结点
cpp
bool Insert(const K& key) {
if (_root == nullptr) {//树为空
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
// 寻找插入位置
while (cur) {
parent = cur;
if (cur->_key <= key) {
cur = cur->_right;
}
else{
cur = cur->_left;
}
}
// 创建新节点并插入
cur = new Node(key);
if (parent->_key < key) {
parent->_right = cur;
} else {
parent->_left = cur;
}
return true;
}2.3 删除操作
首先查找元素是否在二叉搜索树中,如果不存在,则返回false。
如果查找元素存在则分以下四种情况分别处理:(假设要删除的结点为N)
- 要删除结点N左右孩子均为空
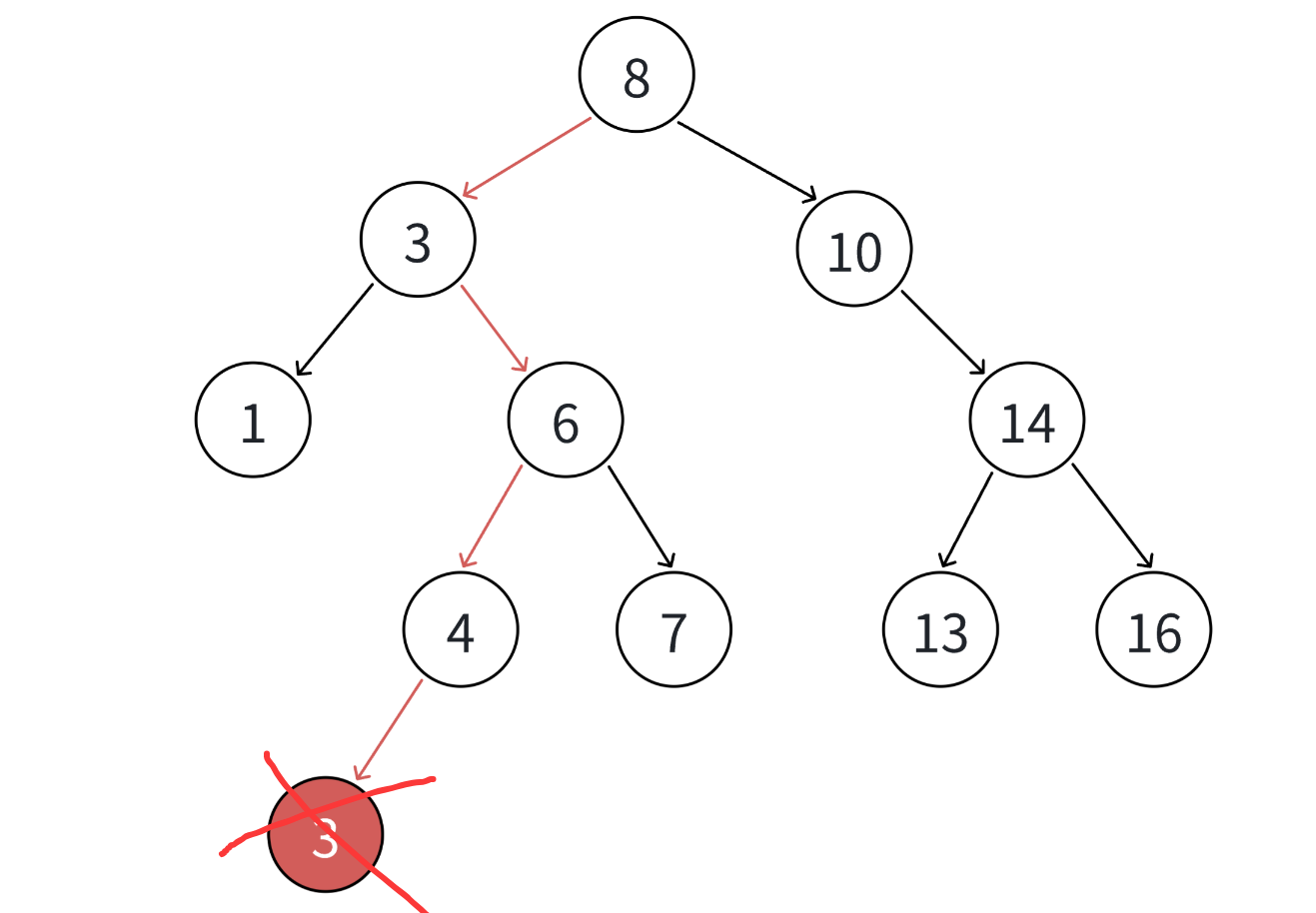
- 要删除的结点N左孩子位空,右孩子结点不为空,那么删除节点的父节点则应该指向删除节点的右孩子
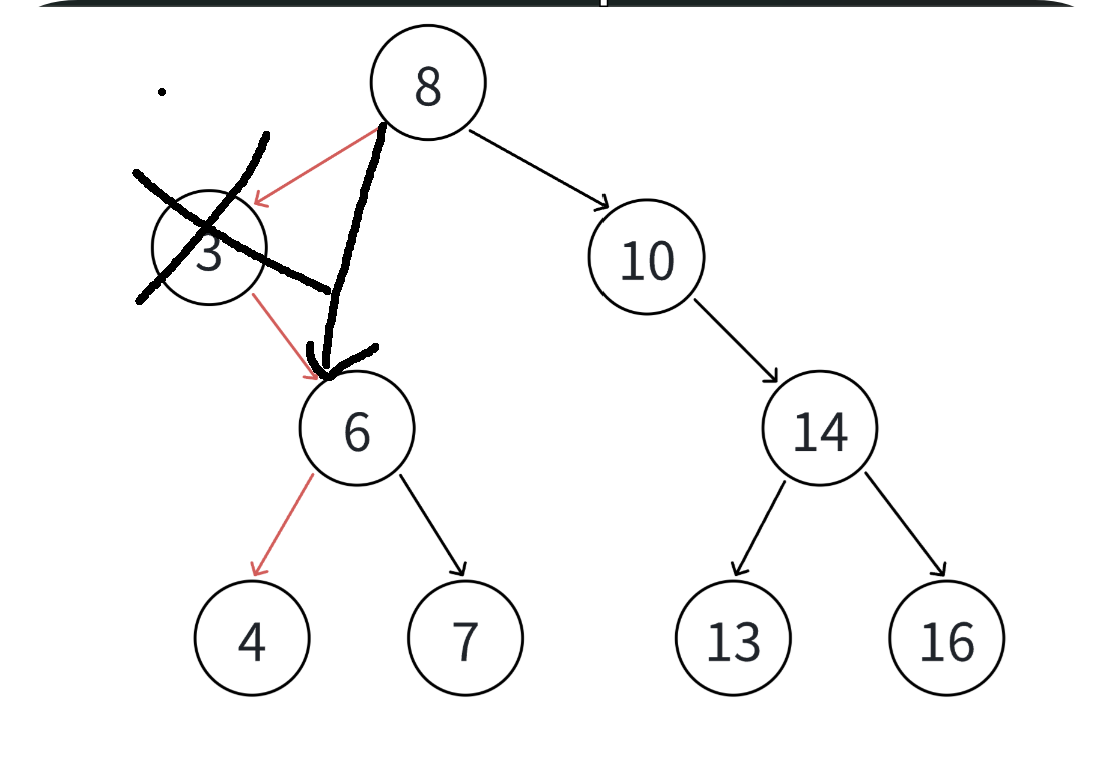
- 要删除的结点N右孩子位空,左孩子结点不为空,那么删除节点的父节点则应该指向删除节点的左孩子
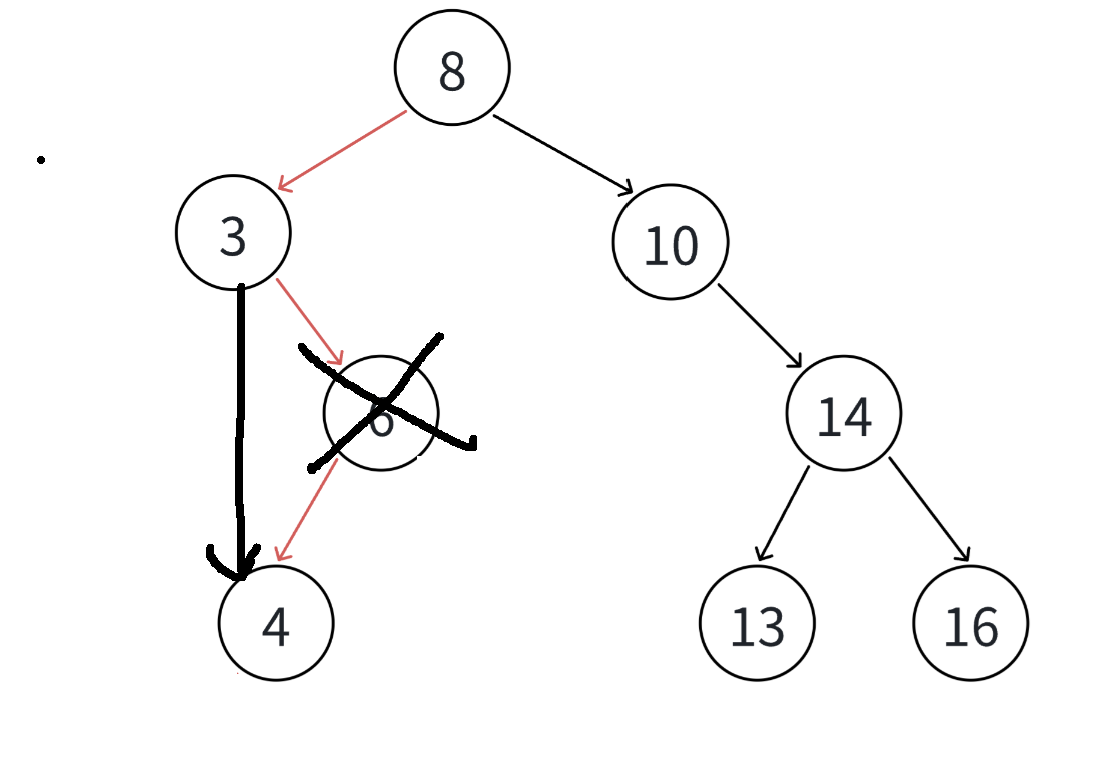
- 要删除的结点N左右孩子结点均不为空,那么这也是最复杂的情况
如果直接删除该节点,其父节点该指向哪里?左孩子还是右孩子?无法判断
因此我们使用替代法
对于要删除的节点N
-
我们在N的左子树中找到最大的节点,然后把值替换给N,随后删除该节点
-
我们也可以在N的右子树中找到最小的节点,然后把值替换给N,随后删除该节点
上面两种方法任意一个都可以
假设是方法2,如何在右子树中找到最小的节点?因为搜索二叉树一一定保证左子树的任意节点的值都小于自己,右子树的任意节点的值都大于自己,因此对于右子树我们一直往左孩子遍历,知道下个为空,那么该节点就是最小的
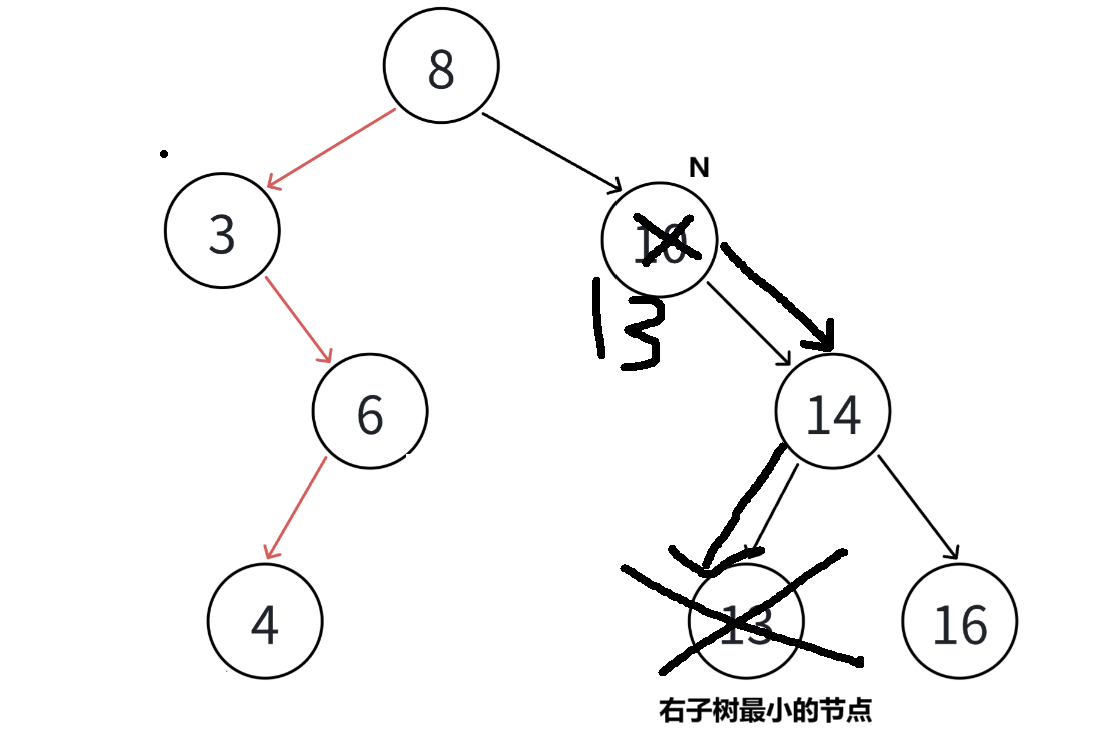
简单替换也不行,如果按这种方式找到了最小的节点,发现该节点还有右孩子,那么则要把其父节点指向右孩子
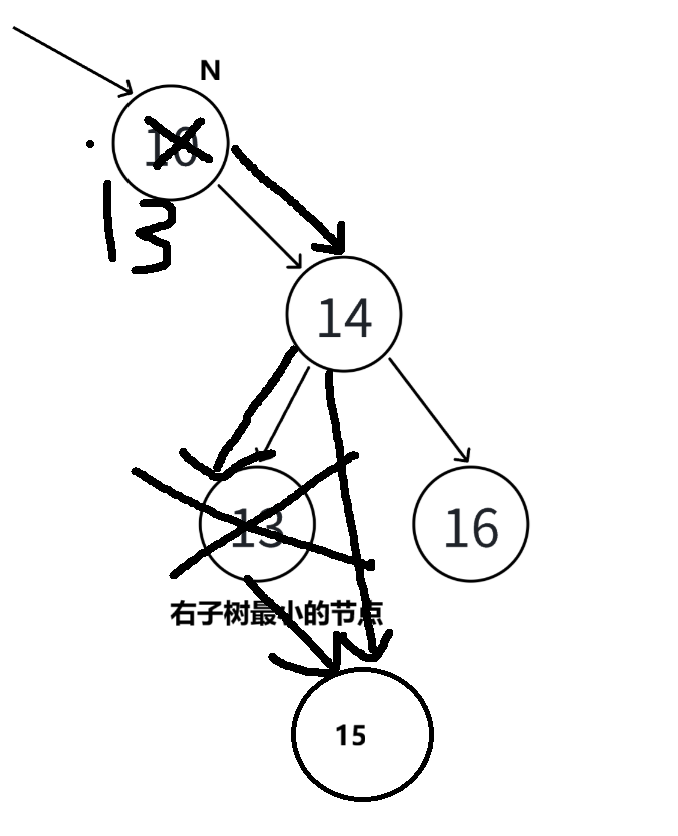
cpp
bool Erase(const K& key) {
Node* parent = nullptr;
Node* cur = _root;
// 查找要删除的节点
while (cur) {
if (cur->_key < key) {
parent = cur;
cur = cur->_right;
} else if (cur->_key > key) {
parent = cur;
cur = cur->_left;
} else {
// 找到要删除的节点,分情况处理
if (cur->_left == nullptr) {
// 情况1&2:左子树为空或左右子树均为空
if (parent == nullptr) {
_root = cur->_right;
} else {
if (parent->_left == cur) {
parent->_left = cur->_right;
} else {
parent->_right = cur->_right;
}
}
delete cur;
} else if (cur->_right == nullptr) {
// 情况3:右子树为空
if (parent == nullptr) {
_root = cur->_left;
} else {
if (parent->_left == cur) {
parent->_left = cur->_left;
} else {
parent->_right = cur->_left;
}
}
delete cur;
} else {
// 情况4:左右子树均不为空 - 替换法删除
// 寻找右子树的最小节点
Node* minParent = cur;
Node* minRight = cur->_right;
while (minRight->_left) {
minParent = minRight;
minRight = minRight->_left;
}
// 替换值
cur->_key = minRight->_key;
// 删除最小节点
if (minParent->_left == minRight) {
minParent->_left = minRight->_right;
} else {
minParent->_right = minRight->_right;
}
delete minRight;
}
return true;
}
}
return false; // 未找到要删除的节点
}4. 二叉搜索树key和key/value使用场景
4.1 key搜索场景:
key即为关键字,我们对于二叉树平衡的判断就是用key来判断的。
假设key为整型,那么很简单,直接整数之间的比较,例如4<5<6,4为5的左孩子,6为5的右孩子
假设key为string,那么就利用字符串的比较方式
总之不管key是什么,反正只需要对应的比较方式就可以
key的搜索场景实现的二叉树搜索树支持增删查,但是不支持修改,修改key破坏搜索树结构了
场景:小区无人值守车库,小区车库买了车位的业主车才能进⼩区,那么物业会把买了车位的业主的车牌号录入后台系统,车辆进入时扫描车牌在不在系统中,在则抬杆,不在则提示非本小区车辆,无法进入。
cpp
// 车牌识别系统示例
class LicensePlateSystem {
private:
BSTree<string> _plates;
public:
// 添加车牌
bool addPlate(const string& plate) {
return _plates.Insert(plate);
}
// 检查车牌是否存在
bool checkPlate(const string& plate) {
return _plates.Find(plate);
}
// 移除车牌
bool removePlate(const string& plate) {
return _plates.Erase(plate);
}
};4.2 key/value搜索场景
每⼀个关键码key ,都有与之对应的值**value,**value可以任意类型对象
这类似于函数中的映射,也可以把key理解为编号,按照编号的大小排序,查找也是查编号
但是修改的则是key所对应的value
场景:简单中英互译字典,树的结构中(结点)存储key(英文)和vlaue(中文),搜索时输入英文,则同时查找到了英文对应的中文。
cpp
void demoDictionary() {
BSTree<string, string> dict;
// 添加单词翻译
dict.Insert("apple", "苹果");
dict.Insert("banana", "香蕉");
dict.Insert("computer", "计算机");
dict.Insert("programming", "编程");
// 查询翻译
string word;
while (cout << "请输入单词: " && cin >> word) {
auto node = dict.Find(word);
if (node) {
cout << "翻译: " << node->_value << endl;
} else {
cout << "未找到该单词" << endl;
}
}
}5. 二叉搜索树的性能分析与优化
5.1 时间复杂度分析
| 操作 | 最佳情况 | 平均情况 | 最坏情况 |
|---|---|---|---|
| 查找 | O(log n) | O(log n) | O(n) |
| 插入 | O(log n) | O(log n) | O(n) |
| 删除 | O(log n) | O(log n) | O(n) |
说明:
-
最佳情况:树完全平衡时
-
最坏情况:树退化为链表时(输入有序数据)
5.2 二叉搜索树的局限性
普通二叉搜索树的主要问题:
-
性能不稳定:依赖于输入数据的顺序
-
可能退化为链表:当输入有序数据时
-
不平衡:不保证树的平衡性
5.3 解决方案:平衡二叉搜索树
为了解决上述问题,发展出了多种平衡二叉搜索树:
-
AVL树:严格的平衡,旋转操作较多
-
红黑树:近似平衡,实践中性能优秀
-
B树/B+树:适用于磁盘存储的多路搜索树
至于这些更高级的搜索树,我们后面再讲
结语
二叉搜索树作为基础数据结构,在计算机科学中具有重要地位:
-
✅ 二叉搜索树的基本概念和性质
-
✅ 查找、插入、删除操作的原理与实现
-
✅ 键值对模式的实际应用
-
✅ 性能分析和优化方向
虽然普通二叉搜索树在某些情况下会退化为O(n)时间复杂度,但理解它的原理是学习更复杂平衡树(AVL树、红黑树)的基础。在实际项目中,我们通常会使用标准库中基于红黑树实现的map和set,但理解底层原理对于解决复杂问题和性能优化至关重要。