文章目录
- 思维导图
- 前言
-
- 一、希尔排序
-
- [1. 核心原理](#1. 核心原理)
- [2. Python实现代码](#2. Python实现代码)
- [3. 特点总结](#3. 特点总结)
- 二、快速排序
-
- [1. 核心原理](#1. 核心原理)
- [2. Python实现代码](#2. Python实现代码)
- [3. 特点总结](#3. 特点总结)
- 三、归并排序
-
- [1. 核心原理](#1. 核心原理)
- [2. Python实现代码](#2. Python实现代码)
- [3. 特点总结](#3. 特点总结)
- 四、三种高级排序算法对比
- 总结
思维导图
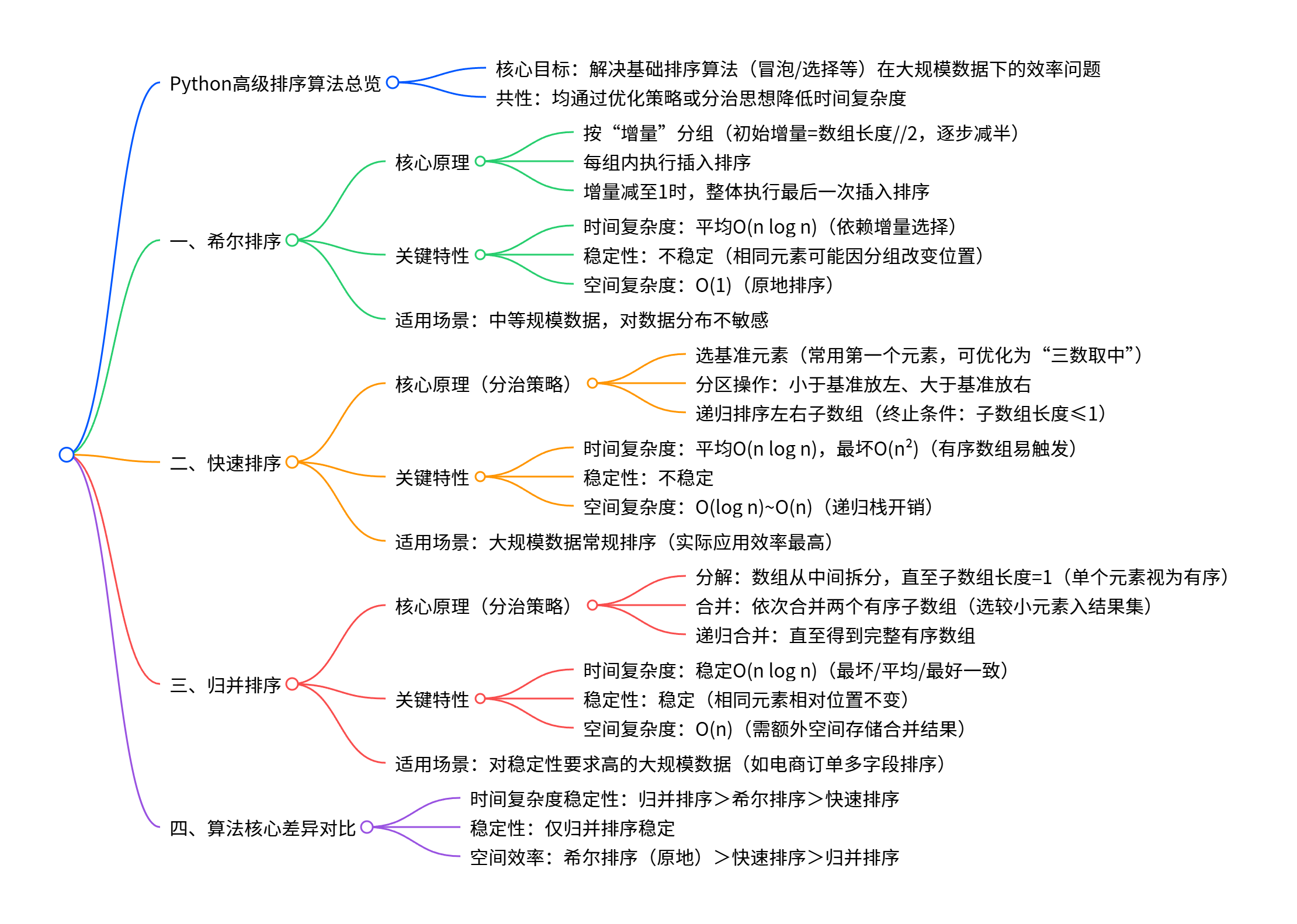
前言
在处理小规模数据时,冒泡排序、选择排序等基础排序算法足以应对,但面对大规模数据,它们较高的时间复杂度会导致效率大幅下降。本文将详细拆解希尔排序、快速排序和归并排序三种高级排序算法,结合Python实现代码,帮助你理解其核心逻辑与应用场景。
一、希尔排序
希尔排序又称"缩小增量排序",是插入排序的优化版本。它通过将待排序数组按一定"增量"分组,对每组执行插入排序,逐步缩小增量直至为1,最终完成整个数组的排序。
1. 核心原理
- 选取小于数组长度的正整数作为初始增量
d1,将数组中距离为d1的元素分为一组,每组内执行插入排序。 - 选取更小的增量
d2(d2 < d1),重复分组与组内插入排序操作。 - 不断缩小增量,直到增量
d = 1,此时数组整体执行一次插入排序,排序完成。
2. Python实现代码
python
def shell_sort(arr):
n = len(arr)
# 初始增量设为数组长度的一半,之后逐步减半
gap = n // 2
while gap > 0:
# 对每组执行插入排序
for i in range(gap, n):
temp = arr[i]
j = i
# 组内元素比较与移动
while j >= gap and arr[j - gap] > temp:
arr[j] = arr[j - gap]
j -= gap
arr[j] = temp
# 缩小增量
gap //= 2
return arr
# 测试示例
test_arr = [8, 9, 1, 7, 2, 3, 5, 4, 6, 0]
sorted_arr = shell_sort(test_arr)
print("希尔排序结果:", sorted_arr)3. 特点总结
- 时间复杂度 :平均时间复杂度约为
O(n log n),具体取决于增量选择。 - 稳定性:非稳定排序(相同元素可能因分组而改变相对位置)。
- 适用场景:适用于中等规模数据,对数据分布不敏感。
二、快速排序
快速排序基于分治策略,通过选取一个"基准元素",将数组分割为"小于基准"和"大于基准"的两部分,再递归对两部分排序,最终实现整体有序。
1. 核心原理
- 从数组中选取一个元素作为"基准"(通常选第一个元素)。
- 重新排列数组:将小于基准的元素放在基准左侧,大于基准的元素放在右侧,基准处于数组中间位置(此过程称为"分区")。
- 递归地对基准左侧的子数组和右侧的子数组执行上述操作,直到子数组长度为1(无需排序)。
2. Python实现代码
python
def quick_sort(arr):
# 递归终止条件:数组长度小于等于1
if len(arr) <= 1:
return arr
# 选取基准元素(此处选第一个元素)
pivot = arr[0]
# 分区:小于基准的元素、等于基准的元素、大于基准的元素
left = [x for x in arr[1:] if x < pivot]
middle = [pivot]
right = [x for x in arr[1:] if x >= pivot]
# 递归排序左右子数组,再合并结果
return quick_sort(left) + middle + quick_sort(right)
# 测试示例
test_arr = [64, 34, 25, 12, 22, 11, 90]
sorted_arr = quick_sort(test_arr)
print("快速排序结果:", sorted_arr)3. 特点总结
- 时间复杂度 :平均时间复杂度为
O(n log n),最坏情况下为O(n²)(如数组已有序,可通过优化基准选择避免)。 - 稳定性:非稳定排序。
- 适用场景:大规模数据排序的首选算法之一,实际应用中效率极高。
三、归并排序
归并排序完全遵循分治思想,将数组不断拆分为两个等大的子数组,直到子数组长度为1,再将排序后的子数组逐步合并,最终得到有序数组。
1. 核心原理
- 分解:将数组从中间拆分为两个子数组,重复拆分操作,直到每个子数组只包含一个元素(单个元素视为有序)。
- 合并:将两个有序子数组合并为一个有序数组,从两个子数组的起始位置开始,依次选取较小的元素放入结果数组,直到所有元素合并完成。
- 递归:重复分解与合并步骤,直到合并为一个完整的有序数组。
2. Python实现代码
python
def merge_sort(arr):
# 递归终止条件:数组长度小于等于1
if len(arr) <= 1:
return arr
# 分解:找到数组中间位置
mid = len(arr) // 2
left = merge_sort(arr[:mid]) # 递归排序左子数组
right = merge_sort(arr[mid:]) # 递归排序右子数组
# 合并:将两个有序子数组合并
return merge(left, right)
def merge(left, right):
result = []
i = j = 0
# 依次选取左右子数组中较小的元素
while i < len(left) and j < len(right):
if left[i] < right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
# 添加剩余元素(左子数组或右子数组中未遍历的元素)
result.extend(left[i:])
result.extend(right[j:])
return result
# 测试示例
test_arr = [34, 64, 25, 55, 12, 22, 11, 90]
sorted_arr = merge_sort(test_arr)
print("归并排序结果:", sorted_arr)3. 特点总结
- 时间复杂度 :最坏、平均、最好时间复杂度均为
O(n log n),性能稳定。 - 稳定性:稳定排序(相同元素的相对位置保持不变)。
- 适用场景:对稳定性要求高的大规模数据排序,如电商订单排序(按价格排序时保持下单时间顺序)。
四、三种高级排序算法对比
| 算法 | 时间复杂度(平均) | 稳定性 | 核心优势 | 适用场景 |
|---|---|---|---|---|
| 希尔排序 | O(n log n) | 不稳定 | 改进插入排序,效率高于基础算法 | 中等规模数据 |
| 快速排序 | O(n log n) | 不稳定 | 实际应用中效率最高 | 大规模数据常规排序 |
| 归并排序 | O(n log n) | 稳定 | 时间复杂度稳定,稳定性强 | 对稳定性要求高的大规模数据 |
总结
希尔排序 是插入排序的优化版,通过 "分组插入 + 增量缩减" 的策略减少元素移动次数,适合中等规模数据。其实现简单,但稳定性和极致效率略逊于后两者。
快速排序 凭借分治思想和高效的分区操作,成为实际应用中平均效率最高的排序算法,是大规模无序数据排序的首选。需注意通过优化基准选择(如随机基准、三数取中)避免最坏情况。
归并排序以稳定的O(n log n)时间复杂度和稳定性著称,适合对排序稳定性有严格要求的场景(如多字段排序)。但其额外的空间开销是需要权衡的因素。