1.前言介绍:
大型语言模型(LLMs)经历了快速的发展,并展现出令人印象深刻的语言理解能力。值得注意的是,LLMs表现出涌现能力,使它们能够解决类似人类的复杂推理任务,如数学计算、思维链推理、少样本提示等。尽管具有这些令人印象深刻的特征,但由于密集连接层内复杂而精细的非线性相互作用,LLMs功能的复杂内部过程尚未得到充分阐明。理解这些潜在机制有助于预测LLMs在训练数据之外的行为,深入了解某些行为的涌现,以及识别和纠正特定模型中存在的错误。
与典型的语言理解任务不同,数学计算任务涉及简洁的问题陈述和明确的正确答案,需要推理和计算过程而不是直接复制来推导解决方案。这些特征使我们能够在不受无关因素干扰的情况下深入了解模型的推理能力。具体而言,需要专注于涉及两个操作数的算术计算任务,即加法、减法、乘法和除法,这些是数学计算的基础。为此,我们创建了涉及计算逻辑的各种类型句子的数据集,如图1中的"3和5的加法等于"。LLMs能够以平均超过80%的高置信度分数提供答案。
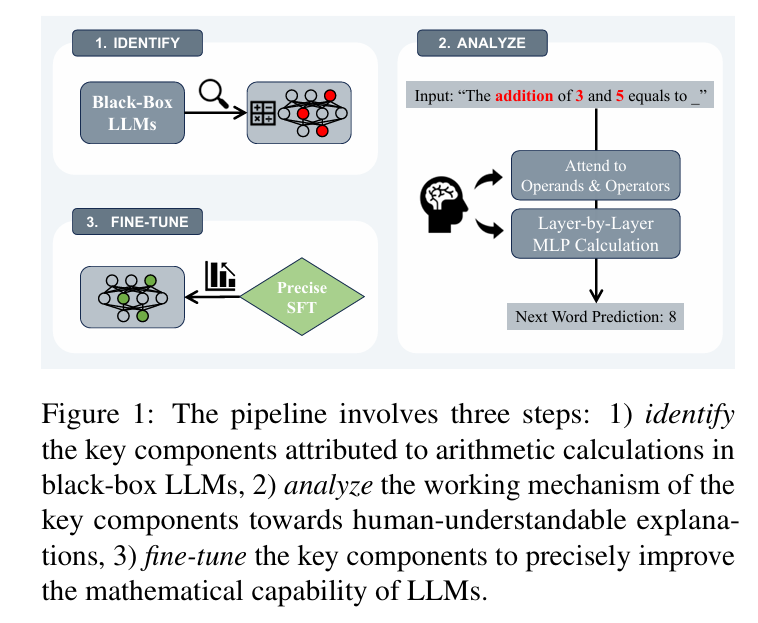
为了揭示这些模型如何正确完成任务(例如"3 + 5 = 8"),我们首先识别LLMs中与任务相关的内部组件。我们对transformer注意力头和多层感知机(MLPs)进行硬干预(Pearl, 2009),以观察它们对预测logits的影响。我们的发现揭示,只有一小部分(< 5%)的注意力头和这些头部之后的MLPs显著影响模型的性能。即,LLMs在完成计算时经常涉及这些注意力头和随后的MLPs。随后,我们敲除这些经常涉及的头部/MLPs来验证它们的忠实性。我们发现,当这些关键的头部/MLPs被敲除时,模型性能急剧下降,导致准确率下降约70%。
为了将已识别的头部/MLPs的工作机制解释为人类可理解的解释,我们对它们的操作"行为"进行了更深入的分析。具体而言,我们调查了关键头部的注意力模式,发现这些注意力头部对数学句子中表示操作数和运算符的tokens表现出强烈的关注 ,对其他非相关tokens表现出相对不敏感。对于MLPs的分析,我们比较了MLPs输入/输出嵌入与数字tokens(即操作数和答案)嵌入之间的相关性。它揭示了MLPs在这些数字关注头部的指导下,将操作数作为输入,并更紧密地反映对应于正确答案的tokens的属性。**这些观察使我们假设LLMs可能最初使用一组头部来从文本中定位算术操作数,随后让MLPs计算出答案。**此外,这些头部/MLPs观察到的行为表现出高度的可迁移性,类似于涉及多位数整数、有理数等的对抗样本。这一实证观察强调了关键头部/MLPs在数学计算中的关键作用。
除了揭示内部机制外,我们还设计了一种有效的策略,涉及**对与数学计算密切相关的特定注意力头和MLPs进行有针对性的微调,从而增强模型的数学能力。**实验结果令人信服:通过微调仅32个注意力头(总共1024个头),我们观察到模型数学能力的显著改善。这种精确的调优方法不仅匹配而且可以超越通过全模型微调实现的增强。
这项工作旨在通过数学计算任务深入探讨LLMs的内部机制,沿着图1所示的"识别-分析-微调"管道。我们的发现揭示了LLMs注意力头的稀疏性,**只有不到5%的头部表现出密切的相关性。这些头部特别关注操作数和运算符,而随后的MLPs逐渐推导出正确答案。**发现的机制显示出强大的跨数据集可迁移性,并激励我们精确微调与计算相关的头部/MLPs以获得更好的数学能力。我们通过实验发现,在改善LLMs的目标能力时,精确调优对非数学任务的影响要小得多。
2.相关工作:
可解释性方法Interpretability Methods
解释大型语言模型(LLMs)的内部机制近年来变得越来越紧迫),特别是当LLMs应用于高风险决策领域如医疗保健、刑事司法和金融时将因果中介分析(CMA)方法应用于解释深度语言模型 ,并已被应用于各种任务,如主谓一致、自然语言推理、事实关联的保持。此外,路径修补通过测量治疗效应如何通过个体神经元或特征之间的节点到节点连接进行中介,扩展了CMA的概念。最近的工作使用路径修补从电路角度解释神经网络,识别了不同能力,包括间接宾语识别、大于计算以及将答案文本映射到答案标签。
数学任务的可解释性Interpretability for Mathematical Tasks
数学能力长期以来一直是自然语言处理领域的研究主题。一些研究调查了LLMs的数学能力,但它们主要关注解释这些模型能做什么,而不是它们如何做。相比之下,其他一些研究更深入地研究了LLM结构,而不将LLM视为不可理解的黑盒。 识别了与算术问题相关的关键注意力层,但缺乏对关键层行为的深入解释和验证。 将因果抽象的方法扩展到理解如何在比较两个数字时遵循指令。提供了关于GPT2-small (0.1B)如何实现"大于"任务的因果解释,但只揭示了受模型小尺寸和数据集缺乏多样性限制的简单现象。
为数学任务微调LLMsFine-tune LLMs for Mathematical Tasks
许多研究通过在微调或推理过程中聚合各种采样推理路径来改善LLMs的数学推理能力。训练并设计了一个推理路径验证器,在推理过程中选择正确的结果。提出在推理过程中采样各种推理路径,然后通过对答案的多数投票或通过验证器得出最终结果。(类似随机森林?Thinking about) 探索使用强化学习方法改善LLMs的数学推理能力。几项工作将拒绝采样的思想与其他技术结合,用于过滤多样化的采样推理路径进行微调数据增强。也存在相关工作定位关键参数以更新以获得更好的任务特定能力。从已经微调的模型中定位一个微小的参数子集到预训练模型上,无需进一步调优。这个子集的选择过程通过优化与任务相关的目标函数和L1范数来确保子集的稀疏性。在我们的工作中,我们通过测量每个组件的因果效应来定位预训练模型的与任务相关的参数,然后精确微调数学任务的关键组件。
3.相关背景知识
大型语言模型(LLMs) 本工作中使用的LLMs包括LLaMA2-7B和LLaMA2-13B。这些是从HuggingFace²免费提供的预训练语言模型。所有这些模型都是仅解码器的transformer,配备多头注意力(MHA)和单个MLP在一个transformer层中。例如,LLaMA2-7B由32个transformer层组成,每层MHA中有32个注意力头。
Transformer架构 Transformer的输入是位置和token嵌入在R^(N×d)中的组合,其中N是输入中token的数量,d是模型维度。遵循(Elhage et al., 2021)中的定义,输入嵌入作为残差流的初始值,所有注意力头和MLPs都从中读取和写入。专注于单个头部,第i层第j个头部由四个矩阵参数化:W^(i,j)_Q, W^(i,j)_K, W^(i,j)_V ∈ R(d×d_H),和W(i,j)_O ∈ R(d_H×d)。为了简化这些参数,我们可以将它们表示为R(d×d)中的低秩矩阵:W^(i,j)_OV = W^(i,j)_O W(i,j)_V和W(i,j)_QK = W^(i,j)_Q (W(i,j)_K)T。QK矩阵用于计算头部(i,j)的注意力模式A^(i,j) ∈ R^(N×N),而OV矩阵确定写入残差流的信息。在前向传播结束时,在未嵌入矩阵W_U将残差流投影到logits之前应用层归一化。
任务和数据集。 我们专注于经典和广泛遇到的数学运算,例如加法、减法、乘法、除法。以加法为例,加法的算术逻辑({A} + {B} = {C})可能自然地出现在句子中。受到GSM8K(Cobbe et al., 2021)和SVAMP(Patel et al., 2021)数学基准中存在的句子风格和形式的启发,我们为加法任务创建了一个数据集,包含基于36个模板的10,000个样本,使用随机的单token名称、对象和数字。为了评估LLMs在计算任务上的性能,我们测量{C} token的预测概率。模型正确预测的平均概率为82%。在本研究中,我们选择语言模型能够正确预测的样本。我们将此过程生成的句子表示为参考数据,使用X_r的符号。
此外,为了满足扰动组件激活的需求,我们创建了另一个数据集,包含反事实句子而不包含计算逻辑,使用X_c的符号。样本的生成遵循两个核心原则:(1)保持从X_r模板派生的语法结构;(2)将负责计算逻辑的几个关键词替换为无关词。例如,来自X_r的句子"42 plus 34 is equal to"被替换为反事实句子"42 nothing 34 is equal to"。这样,它允许直接反映模型对算术计算任务的影响,而不受句子结构或语法的影响。
4.算法:
4.1 关键部分
LLM的计算可以被重组为一个有向无环图(DAG) 。在该图中,每个节点是一个计算组件,包括注意力头、MLP层、残差连接,每条边代表数据流,即前一个节点的输出将被转置到后一个节点的输入 。为了揭示模型预测答案的根本原因,我们采用了称为**路径修补(path patching)**的因果干预技术。通过使用反事实数据X_c扰动目标激活,并使用参考数据X_r冻结其他激活,我们通过比较输出logits来衡量反事实效应。整个过程在算法1中进行了说明。在这项工作中,我们逐一扫描所有节点N,并测量真实标记{C}的输出logit的变化,记录在E_N中。值得注意的是,由于残差操作和MLP分别计算每个标记,因此在END位置(即输入句子中的最后一个标记)修补头部输出足以测量对下一个标记预测的影响。
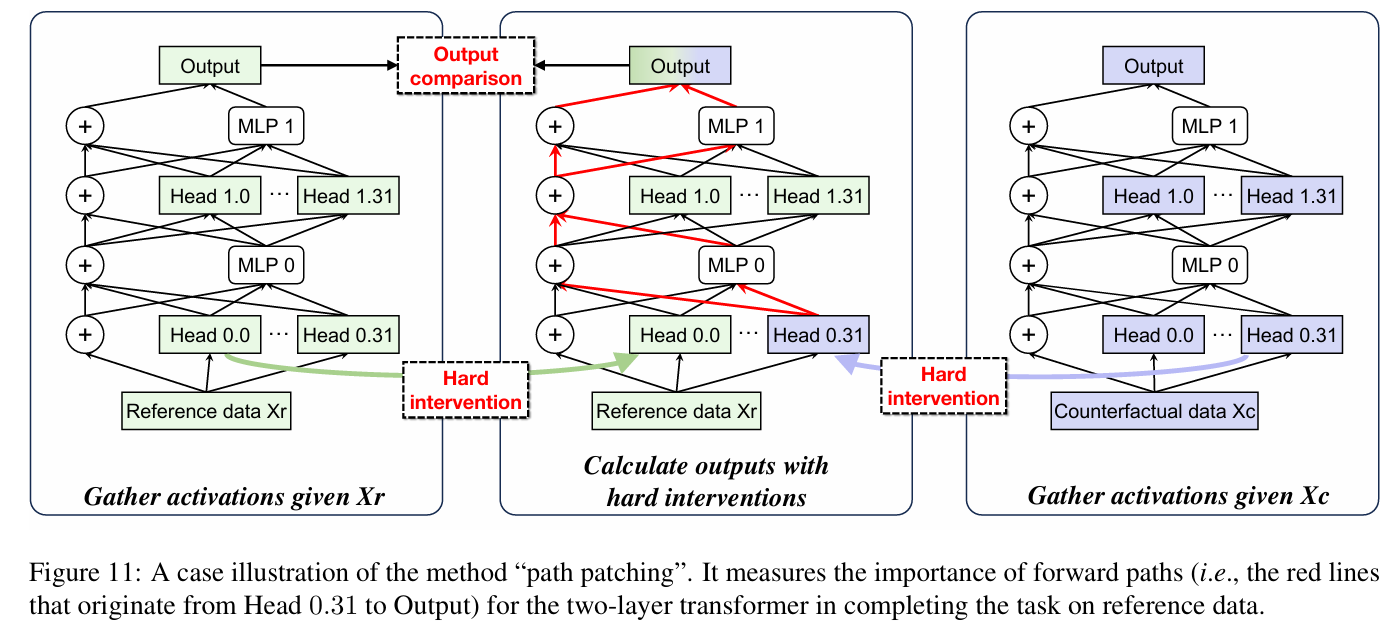
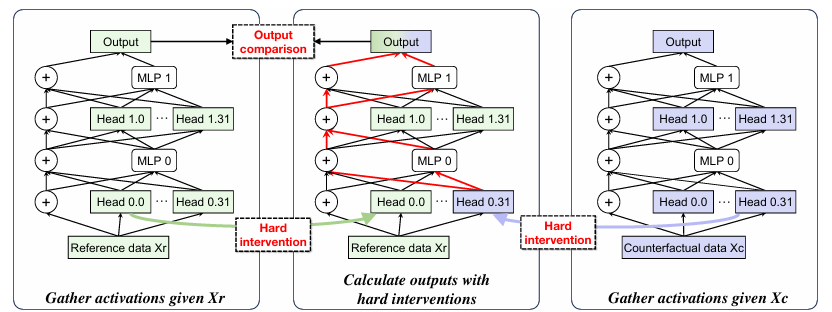
路径修复在分析两个计算节点(发送者→接收者)之间的因果关系方面非常有效。这帮助我们确定发送者是否是接收者的原因,以及它们之间的连接对模型完成任务是否重要。
具体来说,路径修补的整个过程如图所示,其中节点对发送者→接收者被设置为Head 0.31→Output。首先,给定参考数据X_r和反事实数据X_c,收集所有头部的激活以为后续的扰动做准备。然后,我们对Head 0.31进行硬干预,将其扰动为其在X_c上的激活,其中效果将沿着路径集合P进一步传播到输出节点。为了确保对Head 0.31影响的独立观察,P包括通过残差连接和MLPs的前向路径,但不包括其他注意力头部(例如,Head 0.0,...,0.30,1.0,...,1.31)。因此,我们通过对其他头部进行硬干预,将其激活冻结在X_r上。最后,我们获得最终输出logits来测量这种扰动的影响。如果最终logits有显著变化,那么修补的路径:发送者→接收者对模型完成任务是必不可少的。
在这项工作中,为了识别对计算任务有贡献的重要头部,我们扫描所有头部作为发送者节点h,将接收者节点设置为输出logits,并测量真实token {C}的输出logit变化。对模型计算至关重要的路径h→logits应该在修补后导致token {C}的logit大幅下降。值得注意的是,由于残差操作和MLPs分别计算每个token,修补END位置(即输入句子中最后一个token的位置)的头部输出足以测量对下一个token预测的影响。
工作流程WorkFlow:
阶段1:收集参考数据激活
目的: 获取模型在参考数据(X_r)上的标准激活和输出,作为基线。
过程:
- 输入:参考数据 X_r(绿色标识)
- 执行完整的前向传播
- 数据流:X_r → Head 0.0...0.31 → MLP 0 → Head 1.0...1.31 → MLP 1 → Output
- 收集所有组件的激活值
- 记录Head 0.31的激活(绿色箭头指向中间面板)
输出: 基线输出和所有组件的激活值
阶段2:收集反事实数据激活
目的: 获取模型在反事实数据(X_c)上的激活,用于后续干预。
过程:
- 输入:反事实数据 X_c(紫色/蓝色标识)
- 执行完整的前向传播
- 数据流:X_c → Head 0.0...0.31 → MLP 0 → Head 1.0...1.31 → MLP 1 → Output
- 收集所有组件的激活值
- 记录Head 0.31的激活(紫色箭头指向中间面板)
输出: 反事实输出和所有组件的激活值
执行硬干预并计算输出
目的: 通过选择性替换激活来测量特定前向路径的重要性。
过程:
- 输入:参考数据 X_r(绿色标识)
- 硬干预机制:
- 接收来自X_r和X_c的Head 0.31激活
- 选择性地将X_r的激活注入到特定路径
- 路径追踪: 红色线条标记从Head 0.31到输出的关键路径
- 计算干预后的输出
关键路径包括:
- Head 0.31 → MLP 0
- MLP 0 → 求和节点
- 求和节点 → Head 1.0...1.31
- Head 1.0...1.31 → MLP 1
- MLP 1 → 最终输出
模型行为的解释很容易产生误导或不严谨。为了解决这个问题,我们进一步评估了已识别的头部/MLP的重要性,同时确认了其他组件的不重要性。为此,我们采用了一种称为平均消融(mean ablation)的剔除技术来停用单个头部/MLP,并观察它们对模型性能的影响。具体来说,我们将其激活替换为反事实数据X_c上的平均激活,以去除与任务相关的信息。通过观察模型性能的变化,我们可以验证这些关键头部/MLP的作用。
4.2 模式分析 / Pattern Analysis
对于注意力头,我们检查注意力模式A_{i,j} ∈ R^{N×N}来理解哪些tokens被优先考虑。N是输入tokens的数量。具体来说,我们首先收集关键头部在参考数据X_r上的相应注意力模式A_{i,j} 。我们为每个样本提取A_{i,j}的最后一行,分析END位置的Query token与每个Key token之间的注意力分数A_{i,j}^{END} ∈ R^{1×N},并获得相对于样本的平均分数。一般来说,具有最高注意力分数的token类型代表该头部的特征,如数字、数学符号等。
对于MLPs,我们使用未嵌入矩阵作为探针来测量MLPs输入和输出中包含的token内容,特别是数值tokens 。先前的研究,如(Elhage et al., 2021)中报告的那些,已经说明MLP层最初从残差流(即MLP_{in})接收其输入,随后将其输出添加回该流(即MLP_{out}) 。让W_U表示未嵌入矩阵,W_U[*]表示对应于特定token的未嵌入向量。我们计算MLP_{in}、MLP_{out}与W_U[{A}]、W_U[{B}]、W_U[{C}]之间的余弦相似度,以反映MLP接收和生成的信息。为了隔离MLP对特定数值tokens的具体贡献,我们进一步评估MLP输出和输入的减法,即(MLP_{out}-MLP_{in})/||MLP_{out}-MLP_{in}|| · W_U[{A}]/||W_U[{A}]||。(Geva et al., 2022)的研究表明,每个MLP层的输出token表示可以被表征为影响跨词汇表演化表示的加法更新。
4.3. 精确微调 / Precise Fine-tuning
监督微调(SFT)被广泛用于增强模型的数学能力。精确SFT是一种仅更新与数学能力密切相关的组件而保持其他参数不变的方法。算法2说明了整个过程。对于第i个注意力层,输出矩阵W_O^i 被分割为每个头部的等大小块,表示为[W_O^{i,1}, W_O^{i,2}, ..., W_O^{i,H}]。
算法2 精确微调
输入: 模型M,输入X,关键头部索引Φ,迭代次数I,学习率η,W_θ = W_{Q/K/V/O}(表示查询、键、值和输出权重)
过程:
for (i, j) ∈ Φ do
W_θ^(i,j).requires_grad = True
end for
▷ 激活关键头部
loop I times
L = M.forward(X) ▷ 执行模型前向传播
L.backward() ▷ 计算梯度
for w ∈ W_θ do
w = w - η * w.grad ▷ 使用梯度下降更新参数
end for
end loop根据(Elhage et al., 2021),这个过程等价于独立运行头部,每个头部乘以其自己的输出矩阵,然后将它们添加到残差流中。对于选定的单个头部,精确SFT更新四个矩阵的参数:W_Q^{i,j}, W_K^{i,j}, W_V^{i,j} ∈ R{d×d/H},和W_O{i,j} ∈ R^{d×d}。对于选定的MLP层,精确SFT更新该层内的所有参数。由于只调整一小部分参数,精确SFT提供了更短的训练时间和对模型原始能力的最小影响等好处。
5. 实验
实验组织为三个部分:
(1)通过路径修补识别与计算相关的关键组件,并通过剔除验证它们在实现算术计算中的重要性;
(2)通过检查第已识别组件的注意力模式和嵌入来理解它们的行为;
(3)通过数学基准上的精确监督微调来改善数学能力。
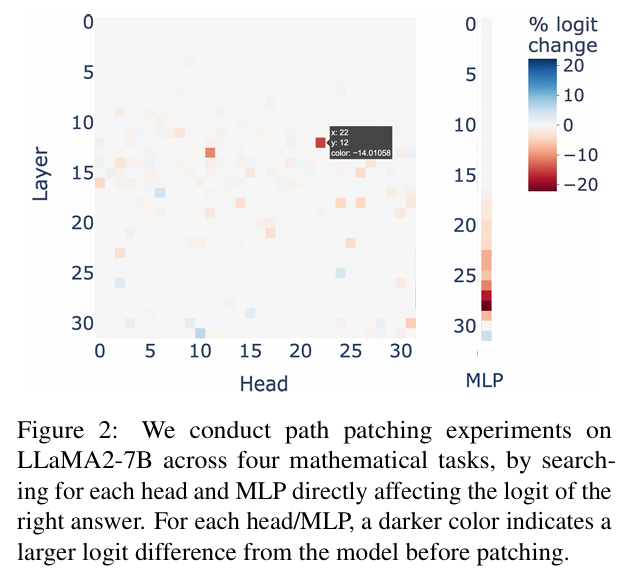
5.1. 识别与计算相关的组件 / Identifying Calculation-related Components
关键头部的位置。 图2可视化了每个头部的影响。红色方块表示对输出有显著积极影响的头部,而蓝色方块表示有负面影响的头部。我们观察到:(i)只有少数头部对输出有值得注意的影响。例如,当修补头部12.22³时,token {C}的logit有14.0%的显著下降。logit变化超过-5%的头部被分类为"关键头部"。(ii)发现的关键头部主要位于中间层。具体来说,对于LLaMA2-7B,关键头部从第12层开始出现,主要集中在第12层和第17层之间。其他LLMs中关键头部的更多分析可以在附录C中找到。
关键MLPs的位置。 图2的最后一列可视化了每个MLP层对真实token {C}的logit的影响。我们观察到,在已识别头部之前的MLPs(0-16)对输出几乎没有影响(约±0.0%)。 相比之下,在第17层之后,MLPs表现出更大的影响(约±10.0%)。这表明MLPs参与了计算。 我们假设这些组件在语言模型完成计算任务的能力中发挥重要作用。
精确SFT改善数学能力Precise SFT improves mathematical ability
监督微调(SFT)是一种通过微调LLMs内的所有参数来增强数学能力的有效方法,为清晰起见,我们称之为"全SFT"。我们采用与全SFT相同的训练设置进行精确SFT。精确SFT有效地增强了数学能力,在四个不同的数学数据集上平均提高了15%。它匹配或超越了全SFT的改进。例如,精确SFT在SVAMP数据集上比全SFT高出5.5%,在GSM8K上高出2.8%,突出了其改善LLMs数学能力的卓越能力。全SFT在数学和通用能力之间存在权衡,导致MMLU和CSQA上约5%的下降。相比之下,精确SFT有效地保持了模型的原始性能。精确SFT的进一步优势是训练时间的显著减少,这是由于需要调整的参数大幅减少(少于1%)。这导致LLaMA2-7B和LLaMA2-13B上的时间减少至少三倍。总体而言,精确SFT为提升LLMs的数学能力提供了有效方向。
消融研究Ablative studies
精确SFT的核心挑战是确定要调整的最佳数量和特定组件。我们进行了改变头部和MLPs数量的实验。我们发现微调32个头部在不同数量的涉及头部中产生最佳平均改进。我们还比较了MLPs的引入。我们观察到,随着**更多MLPs的添加,数学能力提高了2.1%,但通用性能将下降1.5%。前3个MLPs产生了最佳综合结果。**然而,即使引入单个MLP也可能将计算效率降低15%。未来的工作将探索如何更精确地微调MLPs。
6. 结论 / Conclusion
在本文中,我们识别、分析并微调了负责LLMs数学计算能力的内部组件。语言模型经常涉及稀疏头部来特别关注操作数和运算符,以及随后的MLPs来计算出答案。我们对与计算相关的头部/MLPs应用精确调优以获得更好的数学能力,与调优所有参数相比,对非数学任务的影响更小。这些发现有助于更好地理解LLMs的内部机制。
LLaMA2-7B在加法任务上的注意力模式可视化
-
注意力分布模式: 图中显示了不同层和头部之间的注意力权重分布,颜色深浅表示注意力强度。
-
关键头部识别: 通过可视化可以清楚地看到哪些头部对数学计算任务最为重要,这些头部通常表现出对操作数和运算符的强烈关注。
-
层次化处理: 不同层级的注意力模式反映了模型从低层特征提取到高层语义理解的层次化处理过程。
-
计算流程: 注意力模式揭示了模型如何逐步关注输入中的关键信息(如数字、运算符)来完成计算任务。
本文内容参考于Zhang W, Wan C, Zhang Y, et al. Interpreting and improving large language models in arithmetic calculation[J]. arXiv preprint arXiv:2409.01659, 2024.