此分类用于记录吴恩达深度学习课程的学习笔记。
课程相关信息链接如下:
- 原课程视频链接:[双语字幕]吴恩达深度学习deeplearning.ai
- github课程资料,含课件与笔记:吴恩达深度学习教学资料
- 课程配套练习(中英)与答案:吴恩达深度学习课后习题与答案
本篇为第一课第四周的内容,即4.1到4.7的内容。
4.8 这和大脑有什么关系?是吴恩达老师的一个3分钟拓展,不涉及具体知识,因此就不在笔记里出现了。
本周为第一课的最后一周内容,就像标题一样,我们从第二周的逻辑回归,到第三周的浅层神经网络, 再到本周的深度神经网络的概念层层递进,第一课内容主要还是对神经网络框架的基本介绍,因此本周实际上的主要内容还是对深层神经网络传播过程的梳理。
但对于公式的推导,我们在之前的部分已经重复过不止一次了,因此,针对本周的深层神经网络,我会结合课程内容,尽量少列公式计算,多做概念的推导和理解,并在相关部分附上之前对公式详细推导内容的链接。
本篇即是本周的全部理论内容。
1. 深层神经网络
1.1深层神经网络长什么样?
说实话,当进行到这一部分,想必大家也已经猜到深层神经网络的形状了,我们直接用课程里的图:
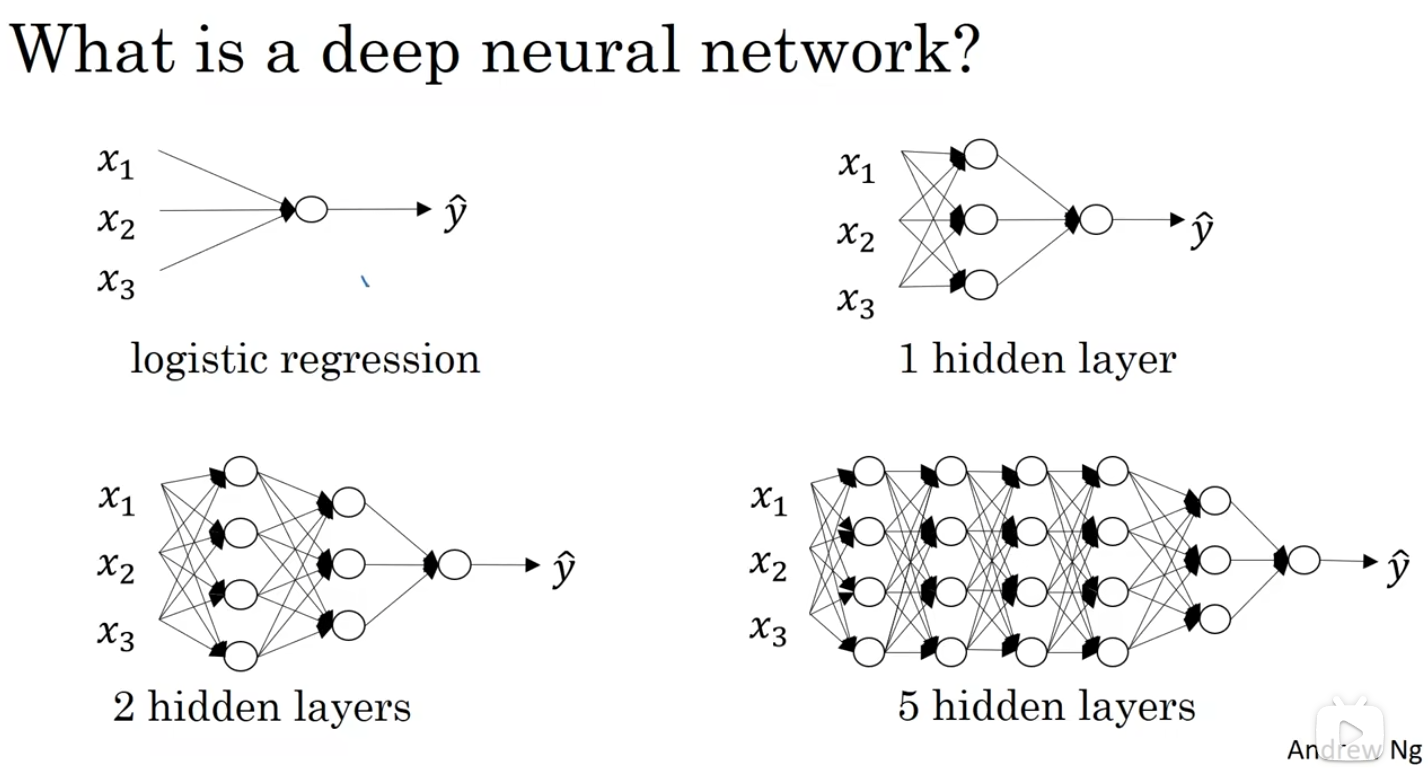
简单来说,相比浅层神经网络,深层神经网络就是神经元更多,隐藏层更复杂的神经网络。
1.2 直观理解深层网络的效果
依旧看课程里的一张图:

图下方的三幅图可以比较好的表现深层网络的效果,我们在浅层提取低级特征,而低级特征经过线性组合和激活后有作为下一层的输入提取更高级些的特征,就像图里的从边缘到整张脸。
要说明的一点是图里的图像处理实际上更常出现在卷积神经网络中,这是后面吴恩达老师在这个系列里单独作为一门的内容。
这里我们只要理解到,随着网络规模的增加,更深的层数能让我们提取更高级的特征即可。
1.3 符号规范
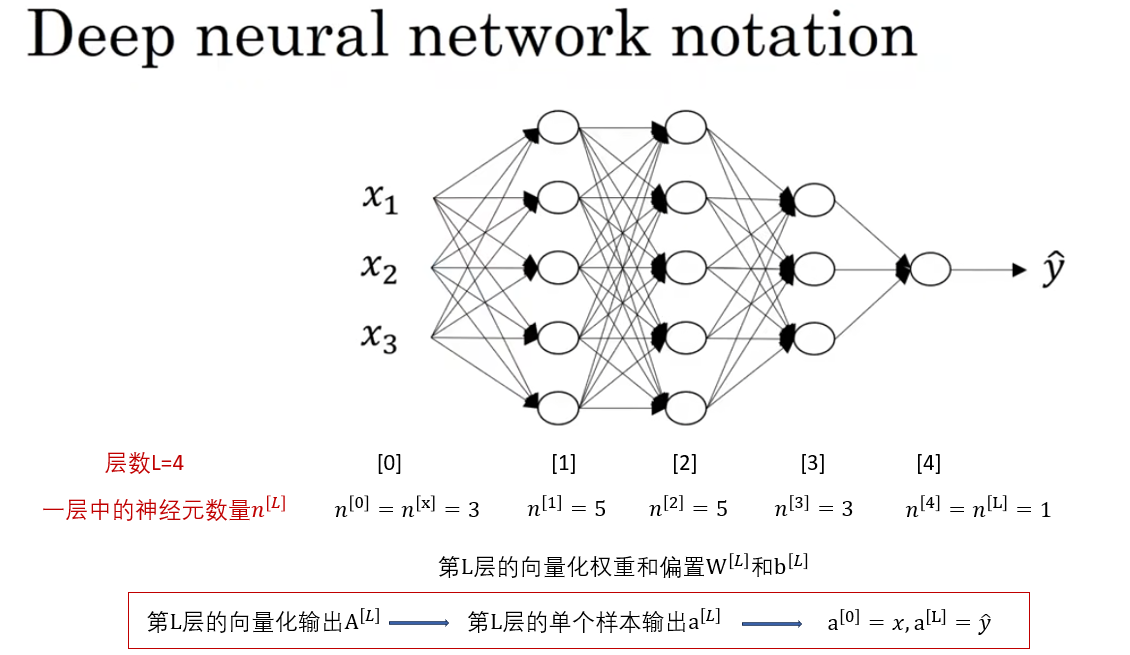
同样如图所示,这些符号我们也在之前使用过很多次了,并不陌生,就不再重复描述了。
1.4 深层神经网络的正向传播
我们用刚刚的网络为例:
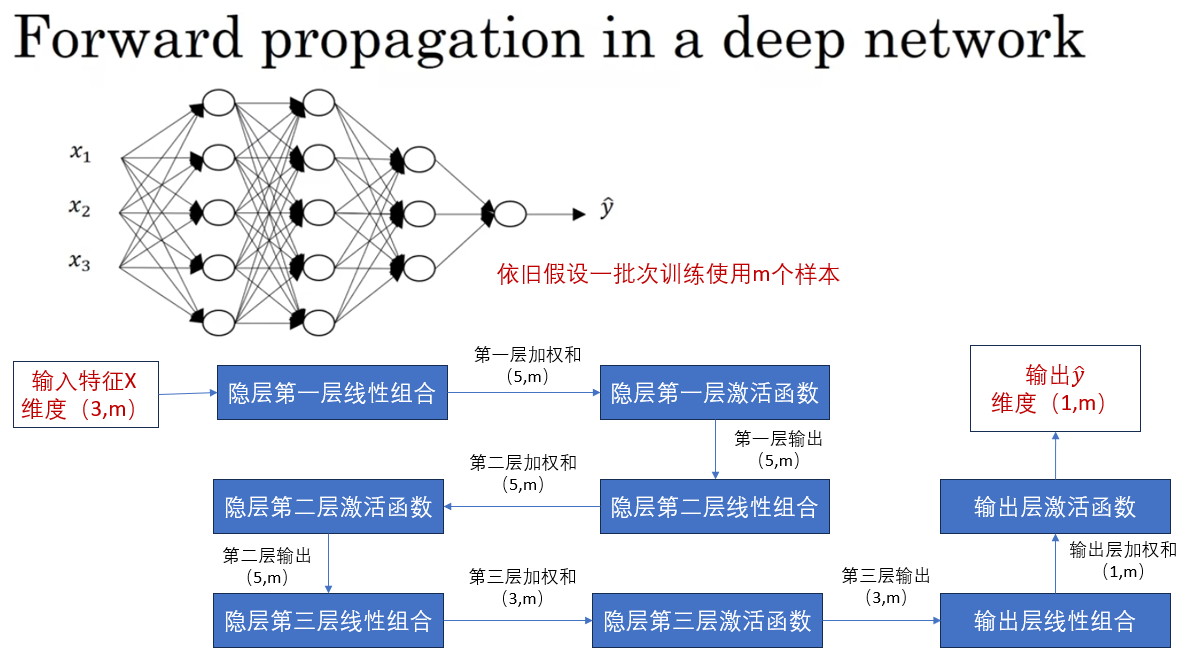
我在图中绘制了这个网络从输入到最终输出的向量化正向传播过程,待会我们会再补充上反向部分。
不难发现,这只是之前的浅层神经网络中又增加了两个隐藏层传播。
我们之前在浅层神经网络中已经推导过这部分的公式计算了,就不再展开了。
正向传播的详细公式推导在这里
1.5 向量化神经网络中的维度变化
我们已经计算过不少次输入在神经网络里的传播,在向量化的计算过程中往往使用矩阵乘法来实现并行计算,这也就伴随着维度的变化。
这里便总结一下维度变化的规律 :
先看贯穿始终的两个公式:
\[\mathbf{Z^{[L]}} = \mathbf{W^{[L]}} \mathbf{A^{[L-1]}} + \mathbf{b^{[L]}} \]
\[ \mathbf{A^{[L]}} = g(\mathbf{Z^{[L]}}) \]
首先,这里的 \(\mathbf{W^{[L]}}\) 的维度应该是\((该层的神经元数量,输入该层样本的特征数)\)
这是因为\(W\)每行的元素个数应和输入的特征数相等,作为每一个特征的权重。
而每多一个神经元就会多一次这样的行为。
推广起来,用符号表示就是:
\[\mathbf{W^{[L]}}: (n^{[L]},n^{[L-1]}) \]
于此同时,每有一组权重,就会有与之配合的一个偏置,因此:
\[\mathbf{b^{[L]}}: (n^{[L]},1) \]
现在,我们通过矩阵乘法即可计算得到:
\[\mathbf{Z^{[L]}}: (n^{[L]},m) \]
而激活函数和求导都不会改变输入维度,所以:
\[\mathbf{A^{[L]}}: (n^{[L]},m) \]
我们总结一下:
| 量 | 维度 |
|---|---|
| \(\mathbf{W^{[L]}}\) | \((n^{[L]},n^{[L-1]})\) |
| \(\mathbf{b^{[L]}}\) | \((n^{[L]},1)\) |
| \(\mathbf{Z^{[L]}}\) | \((n^{[L]},m)\) |
| \(\mathbf{A^{[L]}}\) | \((n^{[L]},m)\) |
| 导数 | 与求导量维度相同 |
2.模块化网络传播
我们通常在代码里才说模块化,这代表着我们对一些需要重复使用的函数进行了一定程度的封装,或者干脆定义了一些对象。
那么当网络深度不断增加,那层级之间的正向传播和反向传播也在不断重复,因此进行模块化也就十分必要,我们来简单看一看这个框架。
2.1.文字传播
我们先补充完刚刚的传播过程,用文字理顺一下各个量的传递。
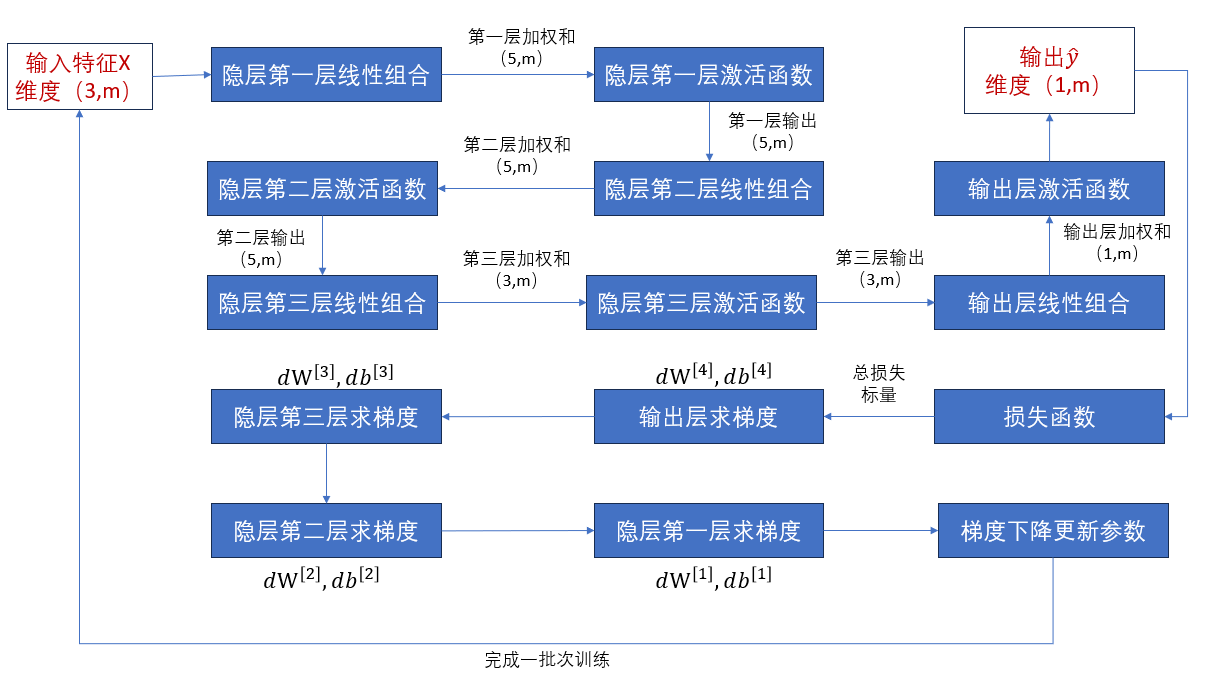
这便是上面的网络结构一批次训练的完整传播过程。
反向传播的详细推导过程在这里
理顺逻辑后,我们把这个过程模块化,用函数,函数的参数,函数的输出的格式再来看一看。
2.2 模块化函数
我们定义层间的正向传播函数forward和反向传播函数backward如下:
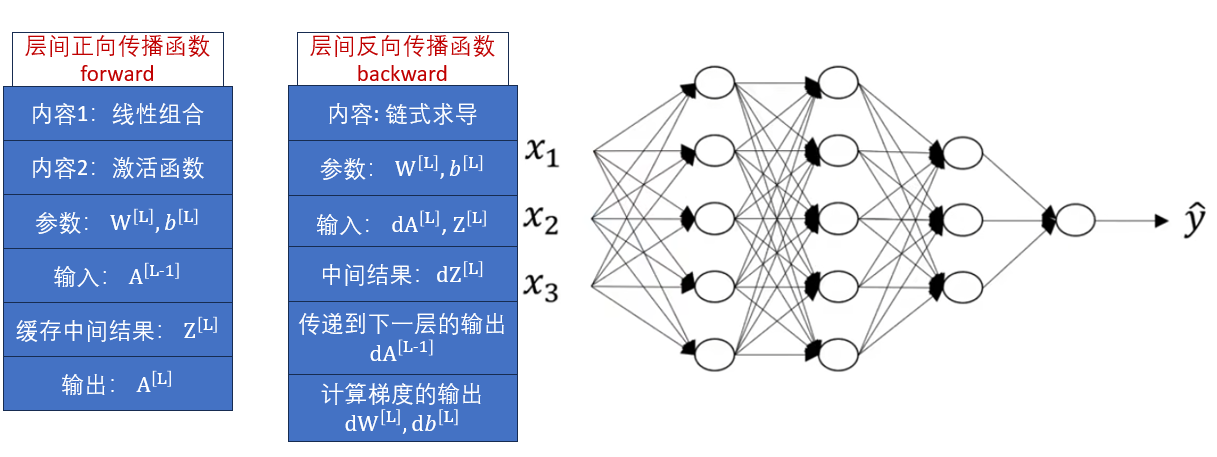
直接解释两个函数的各个属性可能不太清晰,我们直接用右侧的网络来演示这两个函数的使用。
2.3 模块化传播流程
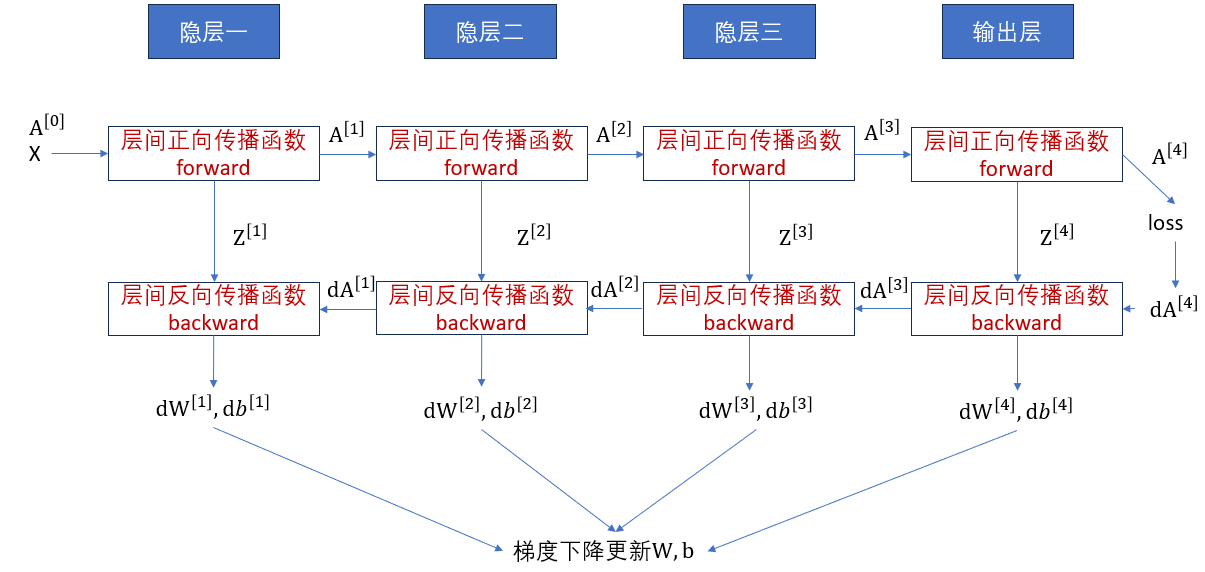
对比图中的过程,我们就可以比较容易的理顺模块化后的传播。
2.4 总结
以上便是第四周课程的全部内容,课程里还提到了超参数的概念,我们在第二周的习题实践部分就已经对其进行了介绍,就不再重复了。
总的来说,经过较多的基础补充,第四周的内容并不多,我们从浅层神经网络再拓展到深层一些的神经网络,并对传播过程中的计算变化进行了总结,给编码实现提供了思路。
下一篇就是本周课程的习题和编码,同时也是课程一的最后一篇。