


文章目录
[3.1.1向零取整 相除](#3.1.1向零取整 相除)
[3.2.1向下取整 相除](#3.2.1向下取整 相除)
上篇:【算法】前缀和(一)原理
一、问题直化前缀和
238. 除自身以外数组的乘积 - 力扣(LeetCode)
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法, 且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]提示:
2 <= nums.length <= 105-30 <= nums[i] <= 30- 输入 保证 数组
answer[i]在 32 位 整数范围内
1.拆拼
整体 拆分成能同类累积部分 拼合成
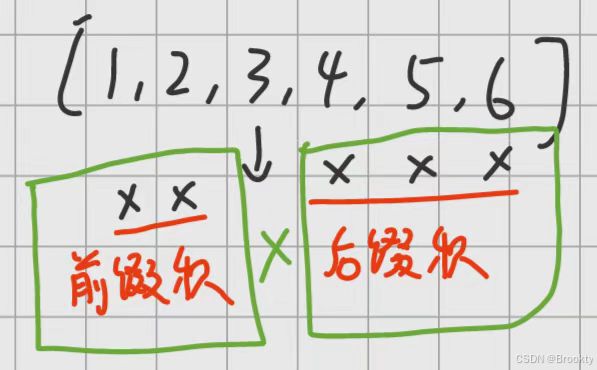
java
public int[] productExceptSelf(int[] nums) {
int n = nums.length;
int[] f = new int[n], g = new int[n], ret = new int[n];
f[0] = g[n - 1] = 1;
for (int i = 1; i < n; i++)
f[i] = f[i - 1] * nums[i - 1];
for (int i = n - 2; i >= 0; i--)
g[i] = g[i + 1] * nums[i + 1];
for (int i = 0; i < n; i++)
ret[i] = f[i] * g[i];
return ret;
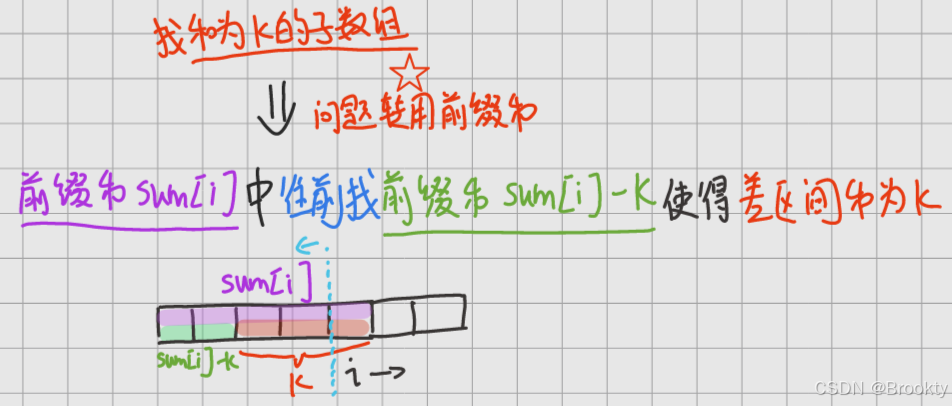
}二、问题转用前缀和
974. 和可被 K 整除的子数组 - 力扣(LeetCode)
给定一个整数数组 nums 和一个整数 k ,返回其中元素之和可被 k 整除的非空 子数组 的数目。
子数组 是数组中 连续 的部分。
示例 1:
输入:nums = [4,5,0,-2,-3,1], k = 5
输出:7
解释:
有 7 个子数组满足其元素之和可被 k = 5 整除:
[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]示例 2:
输入: nums = [5], k = 9
输出: 0提示:
1 <= nums.length <= 3 * 104-104 <= nums[i] <= 1042 <= k <= 104
1.模减消实质
(a + p*k) % p = a % p
2.同余定理
差被++整++除 ++(a - b) % p = 0++ or (a - b) / p = k
=> 减数 模 除数 ++相等++ ++a % p = b % p++
2.1证明
(a - b) / p = k
-> a - b = p*k
-> a = b + p*k
-> a % p = (b + p*k) % p
-> a % p = b % p
3.取模%
3.1计算机

3.1.1向零取整 相除
余数绝对值 最接近0 地相除
3.1.2符号
同被除数
3.2数学

3.2.1向下取整 相除
余数正值 最接近0 地相除
3.2.2符号
正数
3.3两者关系
3.3.1差异
只有 负 % 正 的负数取模 时 结果会不同 (计算机为负、数学为正)
3.3.2转化
计算机 相同等效、不同转化 为 数学 的模结果:(a % p + p) / p
java
public int subarraysDivByK(int[] nums, int k) {
Map<Integer,Integer> map = new HashMap<>();
int sum = 0, ret = 0;
map.put(0,1); // sum = k,sum % k = 0,自己整的区间可以被k整除的是结果,自己整的就是结果,但往前减区间来得 是得不到的,得特判为就是结果地 就开始累积
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
int r = (sum % k + k) % k;
// 找满足的前缀和:
ret += map.getOrDefault(r,0); // (sum - x) % k = 0 => sum % k = x % k,往前找 已存进哈希表里的 前缀和x % k的模 有多少个 等于 当前总区间前缀和sum % k的模
// 存前缀和:
map.put(r, map.getOrDefault(r,0) + 1);
}
return ret;
}