【算法】【动态规划】斐波那契数模型

目录

• 一、动态规划解题模版
• 二、第N个泰波那契数
• [三、⾯试题 08.01. 三步问题](#三、⾯试题 08.01. 三步问题)
• [四、746. 使⽤最⼩花费爬楼梯（easy）](#四、746. 使⽤最⼩花费爬楼梯（easy）)
• 五、91.解码⽅法

一、动态规划解题模版

1. 状态表示：我们一般创建一个一维数组dp，把dp表填满，其中的某一个值就是结果。而状态表示就是指这个dp表中元素的含义；
   1.1. 来源：题目要求，经验+题目要求 ，分析问题的过程中的重复子问题
2. 状态转移方程：dp[ i ] = ?
3. 初始化：保证根据状态转移方程填表时不越界
4. 填表顺序：为了填写当前状态的时候，所需要的状态已经计算过了
5. 返回值：题目要求 + 状态表示

二、第N个泰波那契数

题目链接：第N个泰波那契数

题目描述：

• 
  题目解析：
• 第四个数是钱三个数的和，第一二三个数定下位0 1 1，返回第n个数

解题思路：

1. 状态表示：dp[ i ] 表示的 i 个泰波那锲数
2. 状态转移方程：dp[ i ] = dp[ i - 1] + dp[ i - 2] + dp[ i - 3]
3. 初始化：dp[ 0 ] = 0, dp[ 1 ]= 1, dp[ 2 ] = 1
4. 填表顺序：顺序从左向右填表即可
5. 返回值： dp[ n ]

解题代码：

//时间复杂度：O(N)
//空间复杂度：O(N)
class Solution {
    public int tribonacci(int n) {
        
        if(n < 3) return n == 0 ? 0 : 1;
        //创建dp表
        int[] dp = new int[n + 1];
        //初始化
        dp[0] = 0;
        dp[1] = dp[2] = 1;
        //填表
        for(int i = 3; i <= n; i++) {
            dp[i] = dp[i-1] + dp[i-2] + dp[i-3]; 
        }
        //返回值
        return dp[n];
    }
}

空间优化：只创建长度为三的数组即可：

//时间复杂度：O(N)
//空间复杂度：O(1)
class Solution {
    public int tribonacci(int n) {

        if(n < 3) return n == 0 ? 0 : 1;
        //创建dp表
        int[] dp = new int[]{0,1,1};
        //填表
        for(int i = 3; i <= n; i++) {
            int tmp = dp[0];
            dp[0] = dp[1];
            dp[1] = dp[2];
            dp[2] = tmp + dp[0] + dp[1];
        }
        //返回值
        return dp[2];
    }
}

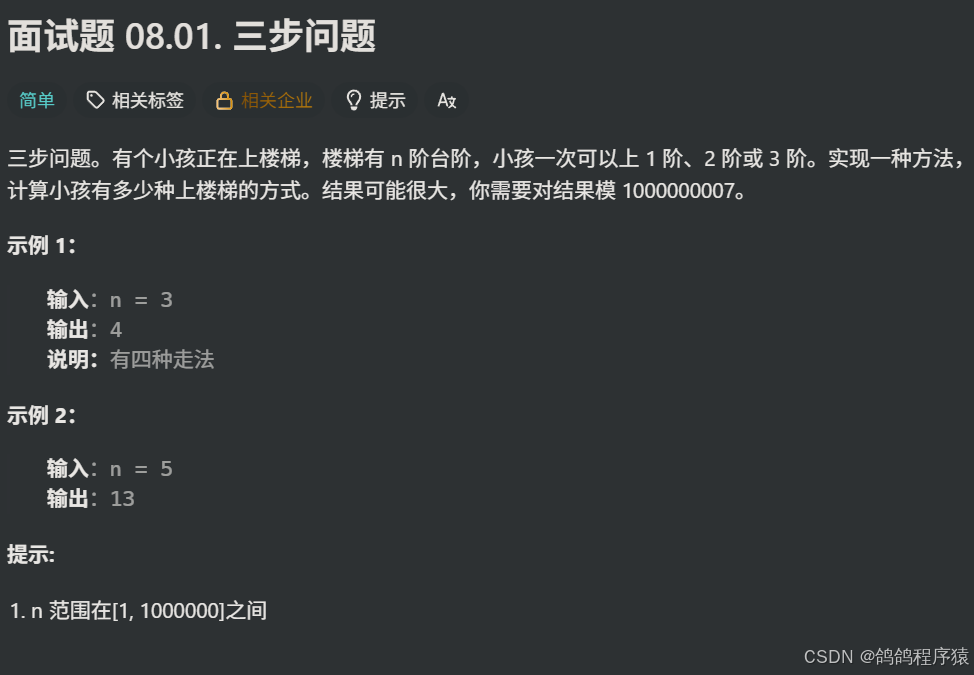
三、⾯试题 08.01. 三步问题

题目链接：⾯试题 08.01. 三步问题](https://leetcode.cn/problems/three-steps-problem-lcci/description/)

题目描述：

• 

题目解析：

• 每一次上楼梯有三个选择： 1 2 3 ，返回走 到第n阶梯 步有多少种走法

解题思路:

1. 状态表示：dp[ i ] 表示第 i 阶的上楼方式种类数
2. 状态转移方程：dp[ i ] = dp[ i - 1] + dp[ i - 2] + dp[ i - 3]
3. 初始化：dp[ 0 ] = 1, dp[ 1 ]= 1, dp[ 2 ] = 2 （小孩有3种走法，那么小孩的上一个台阶的可能就是 i-1， i-2， i-3 ）
4. 填表顺序：顺序从左向右填表即可
5. 返回值： dp[ n ]

解题代码：

//时间复杂度：O(N)
//空间复杂度：O(N)
class Solution {
    public int waysToStep(int n) {
        if(n < 3) return n;
        //建立dp表
        int[] dp = new int[n+1];
        //初始化
        dp[0] = dp[1] = 1;
        dp[2] = 2;
        //填表
        for(int i = 3; i <= n; i++) {
            dp[i] = ( (dp[i-1]  + dp[i-2] ) % 1000000007 + dp[i-3]) % 1000000007;
        }
        //返回值
        return dp[n] ;
        
    }
}

四、746. 使⽤最⼩花费爬楼梯（easy）

题目链接：746. 使⽤最⼩花费爬楼梯（easy）

题目描述：

• 

题目解析：

• 给我们一个cost数组，表示走出这一个台阶需要的花费，
• 可以选择第一步从cost[ 0 ] 还是 cost [ 1 ]开始。
• 让我们返回到达楼顶的最小总花费。

解题思路:

1. 状态表示：dp[ i ] 表示走到第 i 阶的最小花费
2. 状态转移方程：dp[ i ] = dp[i-1]+cost[i-1] 和 dp[i-2]+cost[i-2] 的较小值
3. 初始化：表的长度要比cost大1，表示楼顶
4. 填表顺序：顺序从左向右填表即可
5. 返回值： dp[ n ]
   解题代码：

//时间复杂度：O(N)
//空间复杂度：O(N)
class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int n = cost.length;
        if(n == 2) return Math.min(cost[0],cost[1]);
        //状态转移表
        int[] dp = new int[n+1];
        //状态转移方程
        for(int i = 2; i <= n; i++) {
            dp[i] = Math.min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2]);
        }
        return dp[n];
        
    }
}

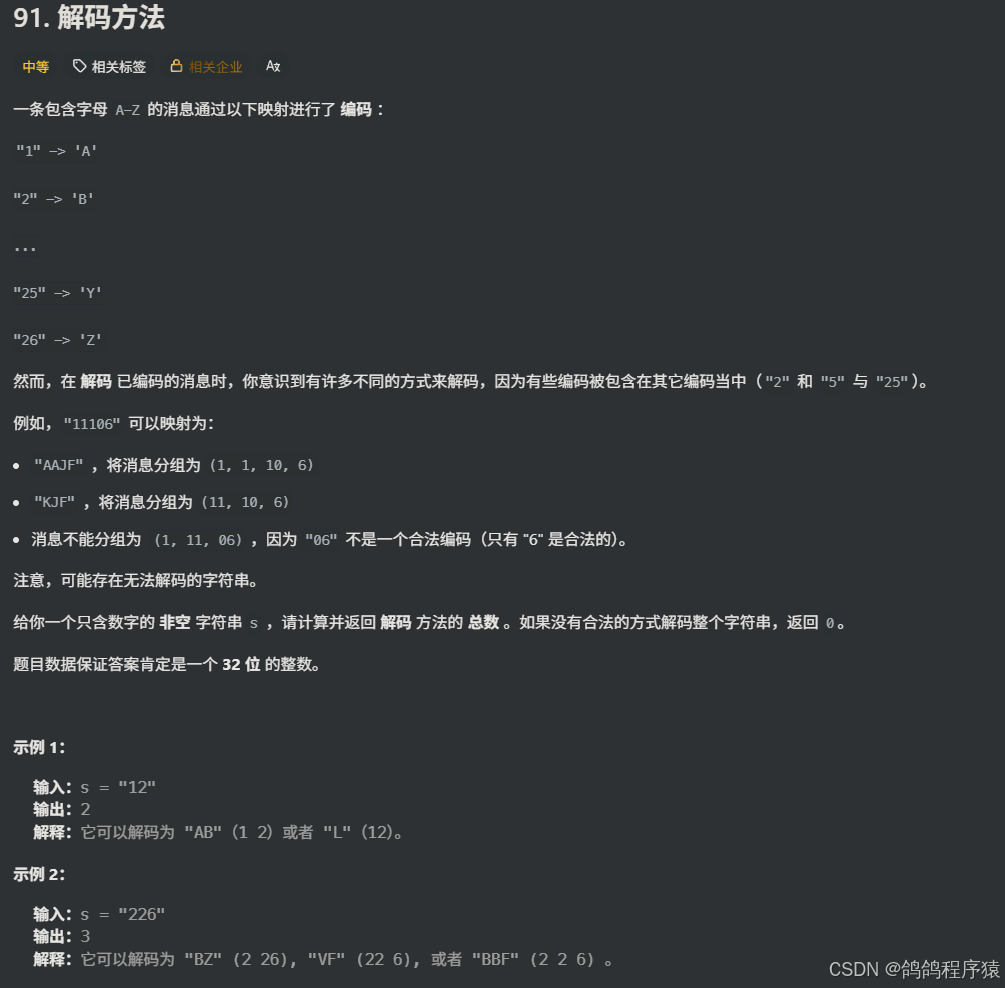
五、91.解码⽅法

题目链接：91.解码⽅法

题目描述：

• 

题目解析：

• 给我们一个编码规则，数字1 - 26 对应表示字母A - Z
• 给我们一个纯数字的字符串，让我们将字符串进行拆分，拆分后的字符串，对应的所有子串都可以对应表示成字母
• 求可以拆分的种数

解题思路:

1. 状态表示：dp[ i ] 表示字符串中 0 到 i 字符的合法拆分结果
2. 状态转移方程：
   2.1. i 位置上字符为 1 到 9 的字符 单独解码成功 dp[ i ] += dp[ i - 1]
   2.2. i 与 i-1位置上的字符组合是 10 到 26 的合法编码 dp[ i ] += dp[ i-2 ]
3. 初始化：
   3.1. dp[ 0 ] ：第一个字符不为0，就dp[ 0] = 1，为0就返回0
   3.2. dp[ 1 ]：该字符不为0，dp[ 1 ] += dp[ 0 ]，与第0个字符组成合法编码10 - 26 ，dp[ 1 ] += 1;

填表顺序：从左到右

返回值：dp[ n-1 ]

解题代码：

class Solution {
    public int numDecodings(String s) {
        //前导0
        if(s.charAt(0) == '0') return 0;

        int n = s.length();
        char[] ch = s.toCharArray();

        //只有一个字符
        if(n == 1) {
            if(ch[0] >= '1' && ch[0] <= '9') {
                return 1;
            } else {
                return 0;
            }
        }
        int[] dp = new int[n];

        //初始化
        dp[0] = 1;
        //初始化第二个元素
        if(ch[1] != '0' && ch[0] != '0') dp[1] += 1;
        int t = (ch[1] - '0') + (ch[0] - '0') * 10 ;
        if(t >= 10 && t <= 26 ) dp[1] += 1;
         
        //填表
        for(int i = 2; i < n; i++) {
            //该字符单独组
            if(ch[i] != '0' ) dp[i] += dp[i-1];
            //与前一个字符组
            t = (ch[i] - '0') + (ch[i-1] - '0') * 10 ;
            if(t >= 10 && t <= 26) dp[i] += dp[i-2];
        }

        return dp[n-1];
    }
}