大模型基础：Rotary Position Embedding(RoPE)

🎯 为什么需要位置编码？

Transformer 模型本身是 排列不变的（permutation-equivariant），也就是说：

❗ 它不知道"词的顺序"！

所以我们必须显式告诉它：

"这个 token 是第几个？"

这就是**位置编码（Positional Encoding）**的作用。

---

📚 传统方法 vs RoPE

方法	代表模型	缺点
绝对位置编码	BERT、原始 Transformer	无法外推，长度受限
相对位置编码	DeBERTa、T5	实现复杂
RoPE（旋转式）	LLaMA、Qwen、Mistral、Phi	✅ 可外推、数学优雅、支持长上下文

📌 RoPE 已成为当前开源大模型的事实标准。

---

🔍 RoPE 的核心思想

RoPE的核心思想，如下图所示：

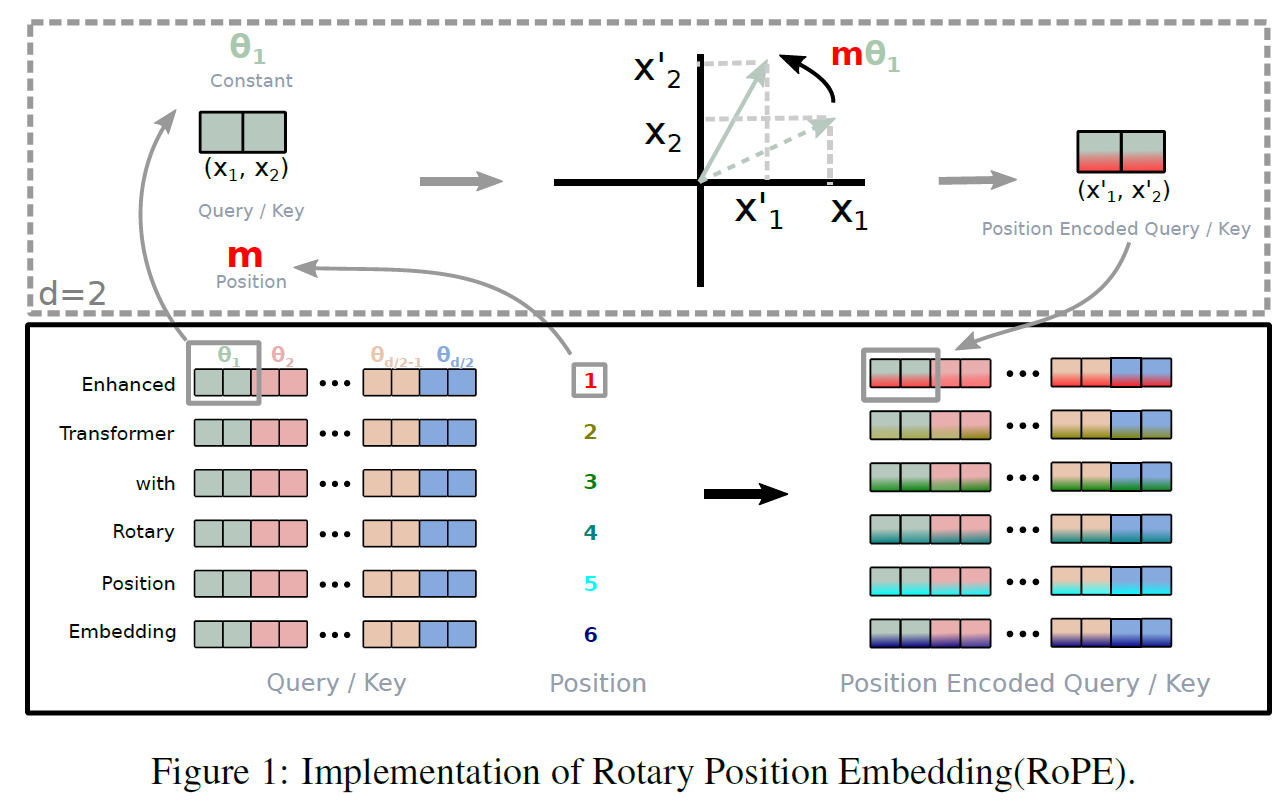
❝ 用 二维向量的旋转 来建模 token 之间的相对位置关系，并通过 Q 和 K 的点积自然体现出"距离越远，影响越小"。 ❞

---

🧮 数学原理

Step 1：基本形式（单个维度）

假设我们有一个向量 x ∈ R d x \in \mathbb{R}^d x∈Rd，我们想给它加上位置信息。

RoPE 对每一对相邻维度进行"旋转"操作：

f m ( x ) = R ( θ m ) x f_m(x) = R(\theta^m) x fm(x)=R(θm)x

其中：

• m m m：token 的位置索引（如第 5 个 token → m = 5 m=5 m=5）
• θ m \theta^m θm：旋转角度，与位置相关
• R ( θ ) R(\theta) R(θ)：二维旋转矩阵：

R ( θ ) = [ cos ⁡ θ − sin ⁡ θ sin ⁡ θ cos ⁡ θ ] R(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} R(θ)=[cosθsinθ−sinθcosθ]

---

Step 2：角度如何定义？

RoPE 使用 频率递减的正弦波 来设置角度：

θ i = 1000 0 − 2 i / d , i = 0 , 1 , ... , d / 2 − 1 \theta_i = 10000^{-2i/d}, \quad i = 0,1,\dots,d/2-1 θi=10000−2i/d,i=0,1,...,d/2−1

然后对于位置 m m m，第 i i i 维的旋转角为：

θ i m = m ⋅ θ i = m ⋅ 1000 0 − 2 i / d \theta_i^m = m \cdot \theta_i = m \cdot 10000^{-2i/d} θim=m⋅θi=m⋅10000−2i/d

📌 这样做的好处：

• 高频部分编码短距离差异
• 低频部分编码长距离趋势
• 支持插值和外推

---

Step 3：应用到 Q 和 K

在 attention 中，我们对 Query 和 Key 应用 RoPE：

Q m = RoPE ( W q x m , m ) K n = RoPE ( W k x n , n ) Q_m = \text{RoPE}(W_q x_m, m) \quad K_n = \text{RoPE}(W_k x_n, n) Qm=RoPE(Wqxm,m)Kn=RoPE(Wkxn,n)

然后计算点积：

Q m T K n = Func ( m − n ) Q_m^T K_n = \text{Func}(m - n) QmTKn=Func(m−n)

👉 关键结论：

点积结果只依赖于 m - n（相对位置），而不是绝对位置 m 或 n！

这就是 RoPE 能捕捉相对位置信息的数学基础。

---

🖼️ 图解：二维旋转示意

      y
      ^
      |     P = (x, y)
      |    /
      |   / 
      |  /   θ = m * θ₀
      | /     
      |/__________> x

位置 m m m 的向量被旋转了 m ⋅ θ m \cdot \theta m⋅θ 角度。

不同位置的向量旋转角度不同，但它们之间的夹角反映了相对距离。

---

💡 为什么叫"旋转"？

因为：

• 每个 token 的 embedding 被看作一组 2D 向量
• 位置信息通过"旋转"这些向量来注入
• 解码时，新 token 继续按规则旋转

就像钟表指针一样，每一步"走一格"。

---

🧱 在 Transformer 中的实际实现

输入：

• x: [B, S, H] → batch, seq_len, hidden_size
• position_ids: [B, S] → 每个 token 的位置索引（如 [0,1,2,...,31]）

输出：

• q_rotated, k_rotated: 注入位置信息后的 Q/K

PyTorch 伪代码：

def rotate_half(x):
    """将 x 拆成两半，在最后维度上做旋转"""
    x1 = x[..., :x.size(-1)//2]
    x2 = x[..., x.size(-1)//2:]
    return torch.cat([-x2, x1], dim=-1)

def apply_rotary_pos_emb(q, k, cos, sin):
    # q, k: [B, H, S, D]
    q_embed = (q * cos) + (rotate_half(q) * sin)
    k_embed = (k * cos) + (rotate_half(k) * sin)
    return q_embed, k_embed

其中：

• cos, sin 是预计算的 cos ⁡ ( m θ ) , sin ⁡ ( m θ ) \cos(m\theta), \sin(m\theta) cos(mθ),sin(mθ)

---

✅ 优势总结

优点	说明
✅ 显式建模相对位置	attention score 自然体现 m-n 关系
✅ 支持长度外推	只要 \\theta 设置合理，可处理比训练更长的序列
✅ 可逆且正交	旋转是正交变换，不改变向量长度，训练稳定
✅ 高效实现	可预先缓存 cos/sin，无需实时计算
✅ 兼容 KV Cache	推理时可动态扩展

---

⚙️ 扩展变体

名称	说明
ALiBi	不用 embedding，用线性偏置建模相对位置
NTK-aware RoPE	调整 θ \theta θ 分布，支持更长上下文
Dynamic NTK	推理时动态缩放，实现无限外推
YaRN	结合 RoPE 与 MoE，进一步提升长文本性能

📌 Qwen 系列就使用了 NTK-aware RoPE 来支持 32K+ 上下文

---

✅ 总结：

Rotary Embedding（RoPE）是一种通过"旋转"Query 和 Key 向量来注入位置信息的技术，它天然支持相对位置建模、长度外推和高效推理，是当前大语言模型中最先进、最主流的位置编码方式。