LeetCode 74.搜索二维矩阵

给你一个满足下述两条属性的 m x n 整数矩阵：

每行中的整数从左到右按非严格递增顺序排列。

每行的第一个整数大于前一行的最后一个整数。

给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

示例 1：

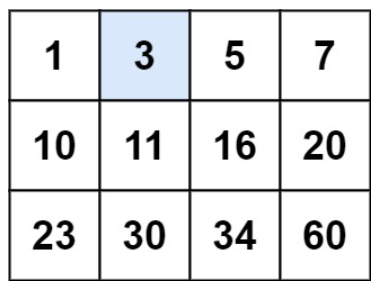
输入：matrix = $\[1,3,5,7$ , $10,11,16,20$ , $23,30,34,60$ ], target = 3

输出：true

示例 2：

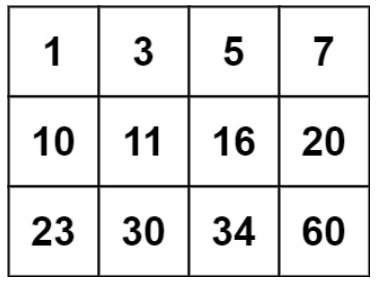
输入：matrix = $\[1,3,5,7$ , $10,11,16,20$ , $23,30,34,60$ ], target = 13

输出：false

提示：

m == matrix.length

n == matrix $i$ .length

1 <= m, n <= 100

-104^44 <= matrix $i$ $j$ , target <= 104^44

法一：先用二分找出目标值所在行，再在行内二分找目标值：

cpp 复制代码

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int l = 0;
        int r = matrix.size() - 1;

        int row = -1;

        while (l <= r) {
            int m = l + (r - l) / 2;
            if (matrix[m][0] > target) {
                r = m - 1;
            } else {
                row = m;
                l = m + 1;
            }
        }

        if (row == -1) {
            return false;
        }

        l = 0;
        r = matrix[0].size() - 1;

        while (l <= r) {
            int m = l + (r - l) / 2;
            if (matrix[row][m] == target) {
                return true;
            } else if (matrix[row][m] > target) {
                r = m - 1;
            } else {
                l = m + 1;
            }
        }

        return false;
    }
};

matrix是m行n列的，此算法时间复杂度为O(logm+logn)，空间复杂度为O(1)。

法二：我们可以从矩阵的右上角开始遍历，如果当前值比目标值小，那么当前值所在行左边的值一定也比目标值小，因此需要到下一行找；如果当前值比目标值大，说明当前值所在列下边的值一定也比目标值大，因此需要到左一列找：

cpp 复制代码

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int row = 0;
        int col = matrix[0].size() - 1;

        while (row < matrix.size() && col >= 0) {
            if (target == matrix[row][col]) {
                return true;
            } else if (target > matrix[row][col]) {
                ++row;
            } else {
                --col;
            }
        }

        return false;
    }
};

matrix是m行n列的，此算法时间复杂度为O(m+n)，空间复杂度为O(1)。