将有序数组转换为二叉搜索树

一、题目内容

给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵平衡二叉搜索树。

示例 1：

复制代码

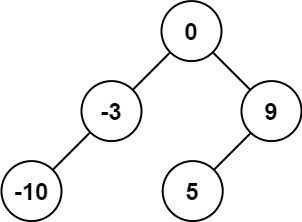
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：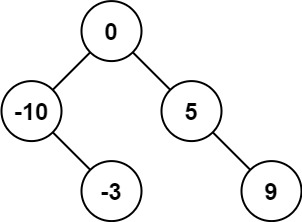

示例 2：

复制代码

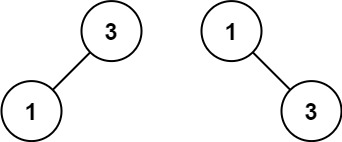
输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

二、源代码（部分)

复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
struct TreeNode* helper(int* nums, int left, int right) {
    if (left > right) {
        return NULL;
    }

    // 总是选择中间位置左边的数字作为根节点
    int mid = (left + right) / 2;

    struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->val = nums[mid];
    root->left = helper(nums, left, mid - 1);
    root->right = helper(nums, mid + 1, right);
    return root;
}

struct TreeNode* sortedArrayToBST(int* nums, int numsSize) {
    return helper(nums, 0, numsSize - 1);
}

三、题目解析

递归边界处理 ：定义辅助函数helper，接收数组nums、左边界left和右边界right。当left > right时（子数组为空），返回NULL，表示当前子树为空。
选择根节点 ：对于非空子数组（left ≤ right），计算中间索引mid = (left + right) / 2，选择nums[mid]作为当前子树的根节点。这一选择保证了左右子树的节点数量尽可能均衡，为构建平衡树奠定基础。
递归构建左右子树：
- 左子树由原数组中[left, mid-1]范围内的元素构成，通过helper(nums, left, mid-1)递归构建。
- 右子树由原数组中[mid+1, right]范围内的元素构成，通过helper(nums, mid+1, right)递归构建。
返回根节点 ：最终构建的树的根节点由helper(nums, 0, numsSize-1)返回，即整个数组对应的平衡 BST。

四、实验总结

算法正确性：
- 满足二叉搜索树性质：由于数组升序，左子树元素（[left, mid-1]）均小于根节点nums[mid]，右子树元素（[mid+1, right]）均大于根节点，符合 BST 的左小右大特性。
- 满足平衡树性质：每次选择中间元素作为根节点，确保左右子树的节点数量差不超过 1，因此整棵树的高度差不会超过 1，是高度平衡的。
时间复杂度：O (n)，其中 n 是数组长度。每个元素会被访问一次（作为根节点），递归过程中没有重复计算，因此时间复杂度与数组长度成正比。
空间复杂度：O (logn)（不考虑输出树的空间）。递归调用的栈深度取决于树的高度，由于是平衡树，高度为 logn，因此栈空间复杂度为 O (logn)。若考虑输出树的存储空间，则为 O (n)（需存储 n 个节点）。
特点与扩展：
- 该实现选择中间偏左的元素作为根节点（mid = (left + right) / 2），若选择中间偏右的元素（如mid = (left + right + 1) / 2），也可构建平衡 BST，结果可能不同但均满足要求。
- 对于升序数组，转换为平衡 BST 的结果不唯一，但该方法是最直接且高效的实现方式。