斯坦福大学 | CS336 | 从零开始构建语言模型 | Spring 2025 | 笔记 | Lecture 6: Kernels，Triton

目录

• • 前言
  • [1. Overview](#1. Overview)
  • [2. Review of gpus](#2. Review of gpus)
  • [3. Benchmarking and profiling](#3. Benchmarking and profiling)
  • • [3.1 Benchmarking](#3.1 Benchmarking)
    • [3.2 Profiling](#3.2 Profiling)
  • [4. Kernel fusion motivation](#4. Kernel fusion motivation)
  • [5. CUDA kernels](#5. CUDA kernels)
  • [6. Triton kernels](#6. Triton kernels)
  • • [6.1 Triton introduction](#6.1 Triton introduction)
    • [6.2 Triton gelu](#6.2 Triton gelu)
  • [7. Pytorch compilation](#7. Pytorch compilation)
  • [8. Triton softmax](#8. Triton softmax)
  • [9. Summary](#9. Summary)
  • 结语
  • 参考

前言

学习斯坦福的 CS336 课程，本篇文章记录课程第六讲：高性能 GPU 代码的编写，记录下个人学习笔记，仅供自己参考😄

website：https://stanford-cs336.github.io/spring2025

video：https://www.youtube.com/playlist?list=PLoROMvodv4rOY23Y0BoGoBGgQ1zmU_MT_

materials：https://github.com/stanford-cs336/spring2025-lectures

course material：https://stanford-cs336.github.io/spring2025-lectures/?trace=var/traces/lecture_06.json

1. Overview

这次课程我们将深入探讨如何编写高性能的 GPU 代码，本次课程安排如下：

我们将先简要回顾 GPU 相关知识，确保大家重新掌握理解后续内容所需的核心概念，接着我们将演示基准测试与性能分析的基础方法，这些技巧不仅对完成作业大有裨益，更能帮助大家编写高性能的 PyTorch 及深度学习代码。

最后我们将实际动手编写几个核心计算内核（kernel），我们将使用 C++ 语言编写 CUDA 计算内核，随后我们将使用 Triton 语言实现相同的功能。最后，我们将采用更简便高效的方式，直接利用 PyTorch 内置的即时编译器（JIT）自动完成优化，随后我们将对这些实现方案进行全面的性能分析和基准测试对比

在整个过程中，我们将深入底层原理展开剖析，我们将深入到底层的 PTX 汇编层面透彻理解这些代码在 GPU 底层实际执行的工作机制，如果时间允许，我们最后会用一个高效的 Triton 版 softmax 实现作为压轴

2. Review of gpus

现在，让我们回顾一下 GPU 的工作原理

当我们使用类似 A100 或 H100 这样的 GPU 时，设备内部会包含多个流式多处理器（SM），每个流式处理器内部都集成有大量可执行运算的计算单元，这些计算单元包括 Int32 整型运算单元和 FP32 单精度浮点运算单元，每个流式多处理器能够同时启动大量线程执行计算任务。

GPU 采用分层存储架构：最外层是容量大但速度较慢的 DRAM（全局显存），而靠近计算核心的多级缓存则具有更快的访问速度。实际上，每个线程都能访问一种名为寄存器文件的超高速存储单元，在编写 GPU 高性能代码时，我们将充分利用这些寄存器来优化程序性能。

GPU 执行模型的基本架构是：多个线程块（blocks）组成计算网格（grid），每个线程块会被调度到单个流式多处理器上，这正是我们编程时需要重点考虑的基本执行单元。特别是在使用 Triton 等框架编写代码时，每个线程块内部包含大量线程，这些线程才是实际执行计算任务的基本单元

因此，当需要对向量元素进行操作时，我们会编写这样的代码：每个线程同时处理该向量中的若干元素，所有线程协同工作，即可完成对整个向量的处理

那么，为什么我们需要这种称为线程块的结构呢？为什么不能直接使用线程和全局大上下文呢？确实，线程块之间可以通过流式多处理器 SM 内的共享内存进行通信，这种交互方式速度极快。在进行矩阵乘法这类运算时，确实需要在不同线程间传递数据，线程块内部，这种数据交换速度极快，但若跨线程块或跨线程组通信，代价就会变得非常高昂

因此，所有需要交互的数据都应尽量保持在同一个线程块或计算单元内部，这样才能确保运算速度达到极致。这样的数据访问速度堪比一级缓存，正是性能最优的理想状态，因此，这种极致可用于线程间的同步操作，但要注意的是，它无法实现跨线程块的全局同步，系统行为实际上不受开发者直接控制

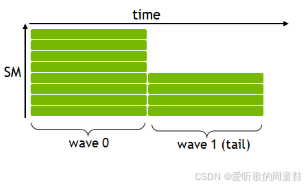
还记得上次课程提到的概念吗？GPU 执行中存在一种称为 "波阵面"（waves）的并行机制，虽然 waves 并非日常编程需要关注的基础概念，但它在性能优化中却扮演着关键角色。在实际运行过程中，线程会被自动分组为连续的 32 线程块（及线程束 /warp），这些线程束就构成了所谓的 "波阵面"，它们会在流式多处理器 SM 中以近乎同步的方式并行执行

因此，我们需要确保所有波阵面的计算负载保持均衡，虽然并非总能实现，但只要条件允许，我们都应尽量做到这一点。因此理想情况下，我们需要精心设计线程块的数量，应当根据流式多处理器 SM 的数量进行合理分配，确保每个波阵面都能获得均等的计算任务。理想情况下，我们设置的线程块数量应当远超过流式多处理器 SM 的数量，这正是我们在编写高性能代码时要着力实现的目标

最后一个概念，或许也是最重要的概念之一，那就是计算强度，我们需要尽可能保持较高的计算强度，我们追求的计算目标是让浮点运算次数（FLOPs）远超内存传输的字节量，这是因为，正如上节课的扩展曲线所示，计算性能的提升速度远远快于内存带宽的提升速度，因此大多数情况下，计算任务往往会受限于内存带宽，导致实际算力无法得到充分发挥

通常来说，矩阵乘法属于计算密集型运算，只要我们优化得当，其他运算基本都会受限于内存带宽，这正是我们需要巧妙优化的重点：要么减少内存受限的操作数量，要么缓解其受制约的程度

OK，以上就是我们对 GPU 架构的简要回顾，希望这些要点大家都还记得

3. Benchmarking and profiling

接下来我们将进入全新内容环节，要编写高性能代码，最关键的是必须养成基准测试和性能剖析的习惯，这道理看似不言自明，经常看到这样的情况：开发者会主观认定某个环节存在性能瓶颈，然后耗费数小时进行优化，结果却发现根本找错了优化方向，虽然这个过程可能充满乐趣，但本质上属于时间资源的错配

因此，只有借助专业级性能剖析工具才能精准定位真正的性能瓶颈，洞悉硬件执行细节，掌握这些关键数据后就能将优化精力精准投放在影响性能的核心代码段上。这里想传达的核心观点是：虽然 GPU 执行机制和手写 softmax 内核等技术细节会不断演进，甚至未来可能直接依赖 PyTorch 编译器的自动即时编译功能，但掌握性能剖析方法论才是根本，性能剖析的必要性永远不会改变

无论工具如何迭代更新，希望大家能深刻理解这个原则：要编写高性能代码，就必须将性能剖析作为常态化开发实践。而理论指导终究有其局限性，其实系统设计是本课程中极具可推导性的核心模块，而硬件架构的推演则更具挑战性。

虽然屋顶模型等理论框架可以提供思考方向，但你的矩阵乘法究竟能跑多快，这往往取决于底层库的版本或硬件配置，不同环节可能因各种原因成为性能瓶颈，其中涉及各种微码技术，存在许多尚未完全掌握的细节，因此归根结底，在开发这类系统时，必须进行端到端的基准测试

下面我们将通过一个具体计算示例来说明，我们要演示的是一个非常简单的多层感知机（MLP），这个模型将采用 128 维的架构，整个网络将包含 16 个隐藏层，模型将采用特定批处理规模，并运行五个不同训练步骤的前向传播和反向传播

具体实现大致如下所示：

class MLP(nn.Module):
    """Simple MLP: linear -> GeLU -> linear -> GeLU -> ... -> linear -> GeLU"""
    def __init__(self, dim: int, num_layers: int):
        super().__init__()
        self.layers = nn.ModuleList([nn.Linear(dim, dim) for _ in range(num_layers)])

    def forward(self, x: torch.Tensor):
        for layer in self.layers:
            x = layer(x)
            x = torch.nn.functional.gelu(x)
        return x

def run_mlp(dim: int, num_layers: int, batch_size: int, num_steps: int) -> Callable:
    # Define a model (with random weights)
    model = MLP(dim, num_layers).to(get_device())

    # Define an input (random)
    x = torch.randn(batch_size, dim, device=get_device())

    def run():
        # Run the model `num_steps` times (note: no optimizer updates)
        for step in range(num_steps):
            # Forward
            y = model(x).mean()

            # Backward
            y.backward()

    return run

上述 run_mlp 函数中首先定义了一个多层感知机（MLP）模型，然后生成一个随机高斯分布输入数据，最后将运行五个训练步骤：先执行前向传播计算，接着进行反向传播，最终将 MLP 输出结果的均值作为返回值，这里甚至没有计算损失函数，这个实现极其简洁，整个过程就是执行 MLP 的前向传播，最后对输出结果做平均池化处理。

其中的多层感知机（MLP）的结构也极其简单，就是多个线性层（linear layers）堆叠在一起，中间还包含了一个数值处理环节，所有结构都清晰易懂

现在我们已经准备好了要运行的这个多层感知机（MLP）代码，接下来我们要做两件事：首先要进行基准测试，也就是做一个耗时统计，知道这个函数的运行耗时是多少；接着要进行性能剖析，也就是深入函数内部找出时间消耗的瓶颈所在

3.1 Benchmarking

那么我们从基准测试开始，基准测试本质上就是测量执行这些操作的实际耗时，在这个案例中，我们仅关注 MLP 函数的端到端执行时间，这其中有些细节需要注意，你可能会纳闷，为什么连调用计时函数这种基础操作都要专门讲解？测试时间确实需要格外谨慎，如果不加以注意，大家在完成第二个作业时很可能会踩到这些坑。

我们为什么要做这些呢？稍后我们将对不同实现方案进行对比，我们将对比 Triton 实现、手写 C++ 代码、PyTorch 原生实现以及 Torch 编译版本，我们想知道费工夫写这个 CUDA 内核到底值不值。

我们还想弄明白，当把矩阵乘法规模扩大时，性能究竟会下降多少，因此我们需要对这些情况进行实际的基准测试，在本次讲座中，我们将全程使用 benchmark 这个基准测试函数，这个函数的具体实现我们会逐步讲解

def benchmark(description: str, run: Callable, num_warmups: int = 1, num_trials: int = 3):
    """Benchmark `func` by running it `num_trials`, and return all the times."""
    # Warmup: first times might be slower due to compilation, things not cached.
    # Since we will run the kernel multiple times, the timing that matters is steady state.
    for _ in range(num_warmups):
        run()
    if torch.cuda.is_available():
        torch.cuda.synchronize()  # Wait for CUDA threads to finish (important!)

    # Time it for real now!
    times: list[float] = [] # @inspect times, @inspect description
    for trial in range(num_trials):  # Do it multiple times to capture variance
        start_time = time.time()

        run()  # Actually perform computation
        if torch.cuda.is_available():
            torch.cuda.synchronize()  # Wait for CUDA threads to finish (important!)

        end_time = time.time()
        times.append((end_time - start_time) * 1000) # @inspect times

    mean_time = mean(times) # @inspect mean_time
    return mean_time

基准测试将执行以下操作：我们将对需要测试性能的 run 函数进行基准测试，首先我们会进行若干次预热迭代，接着会进行多轮正式测试。你可能会好奇：为什么我们要做这个预热环节呢？这是因为当我们首次运行 PyTorch 代码并将其调度到 GPU 时，存在一个关键现象：虽然表面看起来执行速度很快，但实际上首次运行时，系统会在后台编译机器代码，这些编译后的指令才会被发送到 GPU 执行，整个初始化过程涉及诸多底层准备工作，因此必须通过预热迭代来确保基准测试不会受到启动过程的影响。

真正需要测量的是程序达到稳定运行状态后的性能表现，当进行成千上万次迭代测试时，重点在于评估稳定运行阶段的性能表现，而非即时编译 CUDA 代码的瞬时速度，这正是我们需要进行预热操作的根本原因，因此务必预留适当的预热环节

另一个关键要点，稍后使用性能分析工具时会详细说明，那就是必须调用 torch.cuda.synchronize() 这个同步函数，这个函数的作用是什么？GPU 和 CPU 本质上是计算机中两个独立的计算单元，它们基本上可以独立并行运行，执行模型是这样的：我们这里的 Python 代码运行在 CPU 上，当我们运行某些操作时，系统会向 GPU 分派一批 CUDA 内核，它会向 GPU 发出请求："请帮我执行这些运算任务"，GPU 会立即开始执行这些任务，而 CPU 则会继续运行后续指令，CPU 不会等待这些 CUDA 运算完成

这种特性虽然非常适合编写高性能代码，但如果你要进行基准测试，马上就会发现一个明显的问题，在进行基准测试时，如果采用这种 GPU 异步执行而 CPU 同时处理其他任务的模式，实际上你测量的并不是 GPU 的真实执行时间。因此，torch.cuda.synchronize() 的作用就是确保 GPU 和 CPU 达到同步状态，确保所有队列中的任务都已完成执行，使 GPU 和 CPU 在代码执行进度上保持同步

现在，当 GPU 和 CPU 真正达到同步状态时，我们才能准确测量执行时间，我们将对某个操作进行多次计时测量

benchmark("sleep", lambda : time.sleep(50 / 1000))

现在我们要执行计算任务，在这个例子中就是休眠指令，我们将重复执行三次，由于我们设置的休眠时间是 50ms，最终测得的时间应该接近这个数值

当然，在每次运行结束时我们都会调用 torch.cuda.synchronize() 和 CPU 状态同步，这样当 CPU 执行进度领先时，它会在此处等待 GPU 实际完成运算，反之亦然。测试完成后，我们还将计算平均值，由于 GPU 的预热特性等因素可能导致单次测量结果波动，因此需要多次重复测量，取其均值作为最终结果返回

这就是我们的基准测试代码，非常简单，但请记住这里有两个关键点：务必先进行预热运行，务必调用 CUDA 同步操作，只要做到这些，操作就非常简单，如果忘记这些步骤，得到的数据会非常离谱，例如你会看到大型矩阵乘法瞬时完成，这显然是不可能的

现在我们可以对矩阵乘法进行基准测试了

if torch.cuda.is_available():
    dims = (1024, 2048, 4096, 8192, 16384)  # @inspect dims
else:
    dims = (1024, 2048)  # @inspect dims

matmul_results = [] 
for dim in dims:
    # @ inspect dim
    result = benchmark(f"matmul(dim={dim})", run_operation2(dim=dim, operation=lambda a, b: a @ b))
    matmul_results.append((dim, result))  # @inspect matmul_results

我们在 A100 显卡上运行测试，现在我们要针对上面这些不同规模的矩阵进行乘法运算，然后收集每个维度下的运行耗时数据，逐步分析这些基准测试结果

正如预期所见，随着矩阵规模的增大，运行时间呈现出超线性增长的趋势。当然，在较小规模（如 1024 和 2048）时我们发现耗时几乎没有增长，因为执行这些矩阵乘法本身就存在固定的开销成本，数据需要从 CPU 传输到 GPU，内核启动也存在开销

因此超线性增长的趋势并不会一直延续到矩阵尺寸为零的情况，但当矩阵达到足够大的规模后，我们就能清晰地观察到矩阵乘法运算中预期的那种规模增长规律

OK，现在让我们尝试对多层感知机（MLP）进行基准测试，那么我们要如何进行测试呢？

dim = 256  # @inspect dim
num_layers = 4  # @inspect num_layers 
batch_size = 256  # @inspect batch_size
num_steps = 2  # @inspect num_steps

mlp_base = benchmark("run_mlp", run_mlp(dim=dim, num_layers=num_layers, batch_size=batch_size, num_steps=num_steps)) # @inspect mlp_base

我们将扩大上面这个多层感知机的规模，我们将采用 256 维的架构，我们将构建一个四层网络结构，批处理量设为 256，分两步执行，那么完成这个操作需要多少时间呢？

完成该操作需要 6.29 秒。现在我们可以进行一些基础操作，我们可以将步骤数从 2 调整到 5，并对所有配置进行基准测试

step_results = []
for scale in (2, 3, 4, 5):
    result = benchmark(f"run_mlp({scale}x num_steps)", 
                        run_mlp(dim=dim, num_layers=num_layers, 
                            batch_size=batch_size, num_steps=scale * num_steps)) # @inspect result, @inspect scale, @inspect num_steps
    step_results.append((scale, result))  # @inspect step_results

这样就能得到 2 步、3 步、4 步以及 5 步的测试结果。与矩阵乘法的情况不同，当我们调整多层感知机（MLP）的前向传播和反向传播步数时，运行时间会呈现怎样的变换趋势？运行时间应该会呈现线性增长

实际测试结果也确实基本符合这个预期，每个 MLP 运算耗时约 5 秒，从端到端的整体运行时间来看，基本符合 n 乘以 5 秒的线性规律

现在我们可以将网络层数从 2、3、4 层扩展到 5 层，这样调整会带来什么效果？

layer_results = []
for scale in (2, 3, 4, 5):
    result = benchmark(f"run_mlp({scale}x num_layers)", 
                        run_mlp(dim=dim, num_layers=scale * num_layers, 
                            batch_size=batch_size, num_steps=num_steps)) # @inspect result, @inspect scale, @inspect num_layers, @inspect num_steps
    layer_results.append((scale, result))  # @inspect layer_results

这样调整会导致运行时间逐步增加，运行时间依然与网络层数呈线性增长关系。这次同样地，单层网络耗时约五秒，实际约低于这个数值，因此耗时增长幅度基本上是层数的四倍，准确地说，与网络层数呈四倍线性关系，线性增长规律再次显现

显然，无论是计算步骤还是网络层数，都与运行时间呈线性时间关系，这正是我们最终观察到的结果

关于 batch 大小的调整及其结果如下：

batch_results = []
for scale in (2, 3, 4, 5):
    result = benchmark(f"run_mlp({scale}x batch_size)", 
                        run_mlp(dim=dim, num_layers=num_layers, 
                            batch_size=scale * batch_size, num_steps=num_steps)) # @inspect result, @inspect scale, @inspect num_layers, @inspect num_steps
    batch_results.append((scale, result))  # @inspect batch_results

最后模型维度 dim 大小的调整及其结果如下：

dim_results = []
for scale in (2, 3, 4, 5):
    result = benchmark(f"run_mlp({scale}x dim)", 
                        run_mlp(dim=scale * dim, num_layers=num_layers, 
                            batch_size=batch_size, num_steps=num_steps)) # @inspect result, @inspect scale, @inspect num_layers, @inspect num_steps
    dim_results.append((scale, result))  # @inspect dim_results

这里我们就不再做分析了，直接跳过

基准测试部分到此结束，我们可以封装一个实用的函数：先进行预热操作，再调用 CUDA 同步，这样就能精准测量任意代码段的运行时间。在编写代码时，这种规范操作应该始终贯彻，这样就能精准测量你新设计的架构运行所需时长

但要注意的是，当需要定位具体问题时，基准测试这种方法的粒度还是太粗糙了，基准测试只能告诉你代码运行缓慢，却无法精确指出时间消耗在哪些具体环节，因此我们更推荐采用性能剖析的方法

3.2 Profiling

性能剖析能提供更精细粒度的分析结果，这正是我们需要的。性能剖析的优势在于，它不仅能精确显示时间消耗在哪些函数，更重要的是，当你查看调用堆栈时，通常能追溯到与 PyTorch 接口的交互点，定位到实际调用的 PyTorch 组件。

在 PyTorch 底层，还存在着由 CUDA 构成的完整调用体系，通过性能分析工具，你能完整追踪从高层到底层的调用链路，直观看到实际执行的底层指令，这样你就能更直观地理解程序在硬件上的实际执行过程

接下来我们将通过剖析几个简单函数，逐步建立对程序运行机制的直观理解。PyTorch 自带的性能分析工具非常实用，能满足基础的性能剖析需求，这样你无需脱离 Python/PyTorch 环境，就能获得清晰直观的分析结果

首先是休眠函数 sleep 的剖析：

def profile(description: str, run: Callable, num_warmups: int = 1, with_stack: bool = False):
    # Warmup
    for _ in range(num_warmups):
        run()
    if torch.cuda.is_available():
        torch.cuda.synchronize()  # Wait for CUDA threads to finish (important!)

    # Run the code with the profiler
    with torch.profiler.profile(
            activities=[ProfilerActivity.CPU, ProfilerActivity.CUDA],
            # Output stack trace for visualization
            with_stack=with_stack,
            # Needed to export stack trace for visualization
            experimental_config=torch._C._profiler._ExperimentalConfig(verbose=True)) as prof:
        run()
        if torch.cuda.is_available():
            torch.cuda.synchronize()  # Wait for CUDA threads to finish (important!)

    # Print out table
    table = prof.key_averages().table(sort_by="cuda_time_total",
                                      max_name_column_width=80,
                                      row_limit=10)
    #text(f"## {description}")
    #text(table, verbatim=True)

    # Write stack trace visualization
    if with_stack:
        text_path = f"var/stacks_{description}.txt"
        svg_path = f"var/stacks_{description}.svg"
        prof.export_stacks(text_path, "self_cuda_time_total")

    return table

sleep_function = lambda : time.sleep(50 / 1000)
sleep_profile = profile("sleep", sleep_function) 

在 profile 函数中我们再次进行了预热操作，调用 torch.cuda.synchronize() 同步后启动性能分析器同时记录 CPU 和 GPU 的运行时间，接着执行目标运算，再次进行同步操作，最终输出所有运行轮次的平均耗时统计表

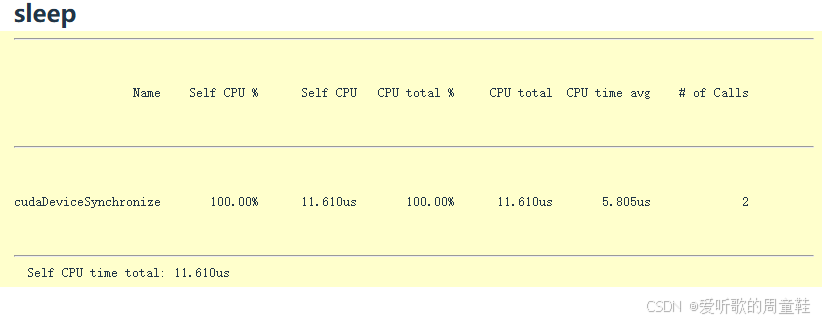
上表展示的是休眠函数性能剖析的结果，我们仔细观察后会发现 100% 的时间都消耗在名为 cudaDeviceSynchronize 同步的操作上，因为当前并没有任何 GPU 计算任务在执行，这实际上是个空操作，剖析这种操作本身就没有实际意义

现在让我们来看一个真正具有计算量的案例：

def run_operation2(dim: int, operation: Callable) -> Callable:
    # Setup: create two random dim x dim matrices
    x = torch.randn(dim, dim, device=get_device())
    y = torch.randn(dim, dim, device=get_device())
    # Return a function to perform the operation
    return lambda : operation(x, y)

add_function = lambda a, b: a + b
add_profile = profile("add", run_operation2(dim=2048, operation=add_function))

现在我们来观察这个基础的矩阵相加运算，这里定义了一个加法函数，接收矩阵 A 和 B 作为输入并将它们相加，run_operation2 是一个辅助函数，它会生成两个随机高斯分布矩阵，然后执行传入的操作参数所定义的运算，这里执行的是两个 2048 维矩阵的加法运算

现在我们对这个运算进行性能分析，得到的结果如上表所示。当我们在 Python 中调用 add 函数时，实际上我们交互的就是 at::native::CUDAFunctor_add... 这个 add 函数，这就是我们需要关心的核心内容。但实际上，就像冰山一样，表面之下还隐藏着更多复杂的工作机制，add 这个操作最终会被被调度到 GPU 上去执行，我们一起来看看这其中到底发生了些什么

首先我们会调用名为 aten 的 PyTorch C 语言接口封装层，这个封装层会确认："好的，我要执行加法运算"，这就是被调用的外层封装逻辑，随后该操作会被分派到一个名为 vectorized_elementwise_kernel 的特定内核，CUDA 向量加法指令实现，CUDAFunctor_add... 才是真正执行加法运算的核心部分。

此外，调用 CUDA 内核启动函数（cudaLaunchKernel） 的过程也耗费了部分时间，这实际上是 CPU 正在接收指令并将其发送至 GPU 的过程，这是内核启动的过程，需要消耗一定时间。最后，CUDA 设备执行同步操作时，我们需要等待 GPU 完成计算并将数据传回，这个阶段同样会耗费时间。仅仅设置同步屏障这个操作本身就会产生时间开销，最终我们得到的总耗时是：CPU 端耗时 1.4ms，而 CUDA 端仅消耗 17us，GPU 端的执行速度确实非常快，相比之下 CPU 端就要慢得多

当我们分析 CPU 耗时时，可以发现 C++ 接口或 C 接口实际上消耗了大量 CPU 时间，这些接口在向 GPU 传输数据时产生了显著的开销。这就是加法函数的执行过程，我们得以窥见其底层运行机制

矩阵乘法的情况也如出一辙：

matmul_function = lambda a, b: a @ b
matmul_profile = profile("matmul", run_operation2(dim=2048, operation=matmul_function))

这里我们正在计算矩阵 A 乘以矩阵 B，即执行矩阵 A 与 B 的乘法运算，这里依然使用 2048 维的方阵进行运算，随后启动性能分析

这次分析结果显示 cutlass_80...，它实际揭示了底层接口执行矩阵乘法的真实调用情况，该操作将调用 NVIDIA 的高性能矩阵乘法 CUDA 库 cutlass 进行运算，随后系统会调度到特定的 cutlass 内核，该内核将采用特定的分块尺寸（tile size）进行计算，此处名称已截断，稍后会展示更详细的版本，它实际上指向一组特定的分块尺寸和线程块数量等参数配置，因此这个模块是参数化的，实际上正是它在执行矩阵乘法运算

我们再次看到底部的两个关键操作：内核启动与 CUDA 设备同步，最后呈现了 CPU 时间与 CUDA 时间的划分，CUDA 计算占据了绝大部分时间，因为矩阵乘法运算本身比简单的向量相加耗时更长

这里再举一个矩阵乘法的例子，这是一个不同维度的案例：

matmul_function_128 = lambda a, b: a @ b
matmul_profile_128 = profile("matmul(dim=128)", run_operation2(dim=128, operation=matmul_function_128))

这里演示的是一个 128 维矩阵的乘法，这个矩阵是 128x128，规模小得多

现在可以看到系统正在直接执行不同的指令，XMMA GMM 运算指令，GMM 是一种矩阵乘法运算类型，表示单精度浮点（float32）运算，从该内核的命名可以看出，这里实际执行的是某种分块矩阵乘法（tiled matrix multiply）的单精度浮点运算，它没有经过 cutlass 框架，而是直接执行了这条特定指令

可以看到，对于小型矩阵乘法运算，系统现在调用了不同的计算内核，由此可见矩阵乘法运算的复杂性。当我们处于这种高度抽象层面时，矩阵乘法运算往往被视为一个整体操作，我们只需调用 A 乘以 B，运算就完成了。但在底层实现中，根据矩阵维度的不同以及硬件配置的差异，系统实际调用的矩阵乘法运算原语可能截然不同，这最终会呈现出天差地别的性能表现

这里分享一个实用技巧：稍后我们会讲到的 Torch compile 工具，它内置了一个选项可以对当前硬件进行矩阵乘法的宏观基准测试，然后自动为你的模型选择性能最优的矩阵乘法子程序，根据实践经验，这个功能往往能带来 10% 的免费性能提升。最妙的是，针对这些细节进行优化确实能在实际应用中带来实实在在的免费性能提升

OK，这又是一个矩阵乘法的经典案例

性能分析工具相比于单纯的基准测试有个绝佳优势，它能让我们直观看到具体调用了哪些 CUDA 内核，通过分析我们可以发现，不同规模的矩阵会触发不同的 CUDA 内核调用，例如 cutlass_80_simt_sgemm_256x128_8x4_nn_align1 来自 cutlass 线性代数库，其命名本身就透露了关键参数，比如计算分块 tile 的尺寸规格

目前来看，这些运算从某种意义上说确实相当基础，无非是些矩阵乘法和加法之类的常规操作，这些运算本质上都是逐元素对应的简单操作。CPU 端的每个运算指令都会直接映射为对应的 GPU 操作，然后被整体调度到显卡执行，因此在整个流程中，真正在 GPU 上执行计算的其实只有单一的核心运算操作

那下面我们来研究两个更复杂的复合运算操作，看看它们的行为模式有何不同

cdist_function = lambda a, b: torch.cdist(a, b)
cdist_profile = profile("cdist", run_operation2(dim=2048, operation=cdist_function))

现在演示的是 torch.cdist 这个运算，它专门用于计算两组矩阵之间的两两欧氏距离，也就是两组词向量的逐对距离度量。它将生成一个庞大的距离矩阵，完整呈现矩阵 A 与矩阵 B 中所有向量对之间的空间关系，这就是 cdist 运算的核心功能。

显然，这个运算的复杂度显著提升了，要计算欧氏距离就必须先处理向量点积运算，再完成平方根计算，我们将在执行 cdist 运算时完整呈现这一计算过程

以下是 cdist 运算的性能剖析结果：

可以看到，这个 PyTorch 的 Python 指令确实通过 C 接口映射到了底层的 cdist 实现，这里显示的是 aten::cdist 函数，其底层实际调用的是 aten::_euclidean_dist 实现，这个运算会分解为一系列基础操作：包括 aten::matmul、aten::mm 等等，因为要计算所有向量间的欧式距离，这些基本运算模块都是必不可少的构建单元。

每当执行这些矩阵乘法、张量拼接和幂运算时，系统都会调用对应的 CUDA 内核指令，这里出现了我们熟悉的 GMM（通用矩阵乘法），也就是矩阵乘法运算，该运算占据了 GPU 78% 的计算时间。这里还涉及数组的拷贝和拼接操作，该操作占用了 6% 的执行时间，而执行幂运算的向量化逐元素内核占用了 5% 的 GPU 时间，求和操作则消耗了 3% 的资源

现在我们得到了 GPU 时间分配的详细底层分析，通过这个分析，我们大致能判断出应该优先优化哪些部分，或许可以考虑优化矩阵乘法运算，这确实是个好主意，因为矩阵乘法占用了 GPU 70% 以上的运算时间

最后要讨论的两个案例是 gelu（高斯误差线性单元）和 softmax 函数，gelu 将作为贯穿本课程的核心案例，这是一种非线性激活函数，这个函数包含双曲正切（tanh）和指数运算的乘积，因此我们将涉及多种运算操作

gelu_function = lambda a, b: torch.nn.functional.gelu(a + b)
gelu_profile = profile("gelu", run_operation2(dim=2048, operation=gelu_function))

我们将执行 A 与 B 相加的运算，随后调用 gelu 函数，以此模拟多层感知机 MLP 中典型的线性与非线性组合结构

可以看到，aten::add 操作对应着 A 加 B 的运算，紧接着是与之对应的 CUDA 运算实现，在代码最后我们实际上已经用 CUDA 实现了一个完整的 gelu 函数，稍后我们会进行分析，这部分计算约占总体运算量的 33%，这个比例相当合理

接下来要讨论的是 softmax 运算：

softmax_function = lambda a, b: torch.nn.functional.softmax(a + b, dim=-1)
softmax_profile = profile("softmax", run_operation2(dim=2048, operation=softmax_function))

这些代码的实现细节我们就不逐一赘述了，毕竟它们都大同小异，但真正值得关注的是，像 softmax 和 gelu 这些核心算子都已经有了专门编写的内核，因此 GPU 并非在执行基础运算单元，而是通过融合算子一次性完成整个计算过程，这样就避免了 CPU 和 GPU 之间的反复数据传输

现在让我们来考虑一个更复杂的情况，之前我们用 MLP 示例作为基准测试的起点，现在我们想优化这个 MLP 让它运行得更快，我们该如何实现这个目标呢？

if torch.cuda.is_available():
    mlp_profile = profile("mlp", run_mlp(dim=2048, num_layers=64, batch_size=1024, num_steps=2), with_stack=True)
else:
    mlp_profile = profile("mlp", run_mlp(dim=128, num_layers=16, batch_size=128, num_steps=2), with_stack=True)

理想情况下，我们需要进行精细化的性能剖析，使用 Torch 性能分析器时，我们会得到类似下面这样的结果

希望你还记得之前提到的那个 MLP 模型，它由多个堆叠的线性层构成，整个流程包含前向传播和反向传播两个阶段。可以看到上表中有在进行反向传播的计算过程，有执行矩阵乘法运算，前向传播执行线性运算，反向传播则对应梯度累加操作。

分析结果表明，大部分计算时间都消耗在矩阵乘法运算上，但你可能会好奇，其余的时间究竟消耗在哪些环节，为何仅有 31% 的时间停留在核心计算环节？另外 60% 的时间消耗在何处呢？虽然显示为 aten::mm 运算，但系统并未捕获到对应的内核执行记录，这确实有些蹊跷。对于如此复杂的模块结构，当前的性能可视化呈现确实不够直观，因此针对这种情况，必须启用专业级的性能分析工具才能准确诊断

这就需要，或者说我们会要求你使用 NVIDIA 的专业工具 Nsight Systems 来进行分析，这正是 NVIDIA 提供的用于深度分析 GPU 行为与性能的专业工具，通过这个工具，我们能够精确观测多层感知机运行时的实际执行情况

从上面的 Nsight Systems 分析图中我们可以看到几个不同的部分，左侧栏中有显示 CUDA 硬件部分，下边是线程信息，上半部分的 CUDA 区域展示的正是 GPU 正在执行的任务，而线程部分则对应着 CPU 的执行情况

下面是分析时添加了注释的代码：

import torch
import torch.nn as nn
import torch.cuda.nvtx as nvtx

def get_device(index: int = 0) -> torch.device:
    """Try to use the GPU if possible, otherwise, use CPU."""
    if torch.cuda.is_available():
        return torch.device(f"cuda:{index}")
    else:
        return torch.device("cpu")

class MLP(nn.Module):
    """Simple MLP: linear -> GeLU -> linear -> GeLU -> ... -> linear -> GeLU"""
    def __init__(self, dim: int, num_layers: int):
        super().__init__()
        self.layers = nn.ModuleList([nn.Linear(dim, dim) for _ in range(num_layers)])

    def forward(self, x: torch.Tensor):
        # Mark the entire forward pass
        for i, layer in enumerate(self.layers):
            # Mark each layer's computation separately
            with nvtx.range(f"layer_{i}"):
                x = layer(x)
                x = torch.nn.functional.gelu(x)
        
        return x

def run_mlp(dim: int, num_layers: int, batch_size: int, num_steps: int, use_optimizer: bool = False):
    """Run forward and backward passes through an MLP.
    
    Args:
        dim: Dimension of each layer
        num_layers: Number of linear+GeLU layers
        batch_size: Number of samples to process at once
        num_steps: Number of forward/backward iterations
        use_optimizer: Whether to use Adam optimizer for weight updates
    """
    # Define a model (with random weights)
    with nvtx.range("define_model"):
        model = MLP(dim, num_layers).to(get_device())
    
    # Initialize optimizer if requested
    optimizer = torch.optim.Adam(model.parameters()) if use_optimizer else None

    # Define an input (random)
    with nvtx.range("define_input"):
        x = torch.randn(batch_size, dim, device=get_device())

    # Run the model `num_steps` times
    for step in range(num_steps):
        if step > 10:
            # start profiling after 10 warmup iterations
            torch.cuda.cudart().cudaProfilerStart()

        nvtx.range_push(f"step_{step}")
        
        # Zero gradients
        if use_optimizer:
            optimizer.zero_grad()
        else:
            model.zero_grad(set_to_none=True)

        # Forward
        with nvtx.range("forward"):
            y = model(x).mean()

        # Backward
        with nvtx.range("backward"):
            y.backward()

        # Optimizer step if enabled
        if use_optimizer:
            with nvtx.range("optimizer_step"):
                #print(f"Step {step}, loss: {y.item():.6f}")
                optimizer.step()
        
        nvtx.range_pop()

def main():
    # Run a larger model if GPU is available
    if torch.cuda.is_available():
        print("Running on GPU")
        run_mlp(dim=4096, num_layers=64, batch_size=1024, num_steps=15, use_optimizer=True)
    else:
        print("Running on CPU")
        run_mlp(dim=128, num_layers=16, batch_size=128, num_steps=15, use_optimizer=True)

if __name__ == "__main__":
    main()

代码中添加了 NVTX 标记，简单来说就是用这些标记来标注代码的关键节点，这样性能分析工具运行时，就能识别这段代码属于 define model 功能块。比如代码中用 range_push 和 range_pop 标记的这段代码，只有在代码中添加了所有这些标注，才能调用性能分析工具

现在看这行标有 NVTX 的代码，可以看到 define model，这是封装好的模型构建调用，接着是 step0、step1、step2、step3、step4、step5 这些标记节点，现在每个步骤都在性能分析工具中清晰地标注出来了，这样我们就能清楚看到模型运行时的每个操作细节

我们从这边开始看，可以看到这段代码的实际计算量其实很小，仅耗时 14s，实际上，性能分析工具的大部分时间都消耗在开销上了，前面这部分时间基本都花在加载库文件上了，耗时相当长，光是初始化环节就耗费了 7.5s

而在 GPU 端，程序运行约 7.5s 后，才真正开始构建模型，注意看上图中的内存占用曲线，7.63s 这个节点正是内存开始分配的时点，此时 GPU 显存占用开始攀升，模型构建在 9.58s 完成，随后 step0 标志着实际运算启动

Note：Nsight Systems 的性能分析请对照着课程视频讲解来看

CPU 和 GPU 之间究竟是如何协同工作的呢？让我们梳理一下当前的执行流程，正如我们之前提到的，当你首次调用 PyTorch 中的某段代码时，系统并不会直接执行它，实际上，系统会实时进行动态编译等操作，这种运行时触发的模块加载属于初始化开销

系统需要完成这些准备工作才能初始化网络层和计算流程，并将相关代码段载入 GPU，这个过程相当耗时，当 step0 初始化完成后，我们放大任意时间片段观察就会发现，这里的每个网络层执行速度都变得极快，

注意这个现象：当我们高亮显示 CPU 端的第一层时，GPU 端对应的第一层执行位置其实并不在此处，正如我们之前强调的，CPU 和 GPU 是两种独立的执行设备。

我们从第零层开始，第零层处理完毕开始处理第一层，此时 CPU 实际上正在将所有 CUDA 命令（即 CUDA 内核）全部发送至 GPU，并已开始启动这些 CUDA 内核。当 CPU 显示 "正在处理第一层" 时，其实际执行的操作是向 GPU 的任务队列提交指令，它发出指令：先执行这个任务，接着执行下一个任务，然后继续执行后续任务，因此 CPU 的运行进度远超 GPU

当 GPU 刚开始执行第一层运算时，CPU 实际上已经处理到第九层了，CPU 的处理进度遥遥领先，它通过维护一个指令队列，持续向 GPU 发送固定数量的 CUDA 内核，因此当达到队列容量上限时，CPU 就会停止继续超前调度任务。当在触及这个临界点之前，CPU 会持续不断地向前推进任务调度，直到达到其极限处理能力

当我们缩小视图范围时可以看到这些计算步骤地进度差异非常大：第零步还在执行，第二步的运算却已经推进了，第一步的计算几乎瞬间就完成了。实际上 CPU 已经领先 GPU 整整一个完整的前向和反向计算步骤了

有个值得注意的现象，在编写语言模型训练代码时，常规操作是这样的：

# Optimizer step if enabled
if use_optimizer:
    with nvtx.range("optimizer_step"):
        print(f"Step {step}, loss: {y.item():.6f}")
        optimizer.step()

我们通常会在迭代过程中打印损失值，表面看来这应该不会影响 GPU 的运行，你可能会想：这不就是个打印语句嘛，能有多大影响呢？仔细想想，这其实会对 GPU 的执行布局产生重大影响，因为要正确执行这个打印语句（CPU 端的操作），CPU 必须先获取损失值，这意味着 CPU 必须等待 GPU 完成损失值计算

接下来我们看看实际会发生什么，正如我们之前提到的，CPU 端的第四步执行时间远早于 GPU 端的对应操作，那现在我们来看看进行性能分析时带有打印语句的版本

现在可以看到第一步和第二步基本实现了同步执行，因为必须等待损失值计算完成后才能继续。现在让我们重新聚焦，看看 CPU 上第一步究竟发生了什么，简单来说，CPU 上第一步的结束点其实也差不多就是优化器步骤开始的地方，首先需要同步 CUDA 流

这个 CPU 端的 CUDA 流同步指令，本质上就是在说：我得等 GPU 完成当前任务，因为 CPU 不能抢在 GPU 前面执行，我正在等待这个损失值计算完成并传回给我，图中的空转操作就是让 CPU 不断等待，直到反向传播步骤完成，才能最终打印出损失值。

损失值打印完毕，现在 CPU 可以继续执行后续操作了，于是 CPU 继续推进，开始发送第二步的运算指令，但当执行到这里时，所有指令都已处理完毕，它又在等待损失值的返回

持续等待反向步骤完成，完成后可以输出损失值了，现在 CPU 又可以继续向前执行了。因此在这种情况下，无论哪种场景，GPU 实际上都保持着满载运行状态，但在极端情况下，比如持续大量打印输出时，实际上会引发 CPU 瓶颈，因为 CPU 必须不断等待 GPU 完成操作，导致无法提前启动后续计算内核

这正是性能分析工具最精妙之处，你能直观看到 CPU 与 GPU 这两个独立设备间的通信状态，这并非一个统一整体，若不借助这些高级性能分析工具，你根本无法观察到这种交互细节

另外想给大家展示之前调试的性能分析工具界面，在 Nsight Systems 中同样可以生成类似的视图界面，只需选定需要分析的操作范围即可，我们将从第三步开始测量若干步骤的性能数据，在这个分析区间内，我们可以聚焦计算核心---实际执行运算的部分

可以看到这里存在多种不同类型的矩阵乘法运算，此外还存在经过向量化处理的元素级运算核函数，这些核函数各自消耗的计算资源也各不相同，我们可以调出事件视图完整展示当前所有正在执行的计算任务，同时还能在统计视图中查看各环节耗时

我们需要统计所有内核的总执行时长，这样我们就能通过这些视图综合分析哪些内核在整体耗时中占比最高。这确实是一款极其强大的工具，它既能从宏观层面展示整体性能瓶颈与优势模块，又能精确跟踪每个内核的启动时序及其对应的 CPU 指令来源

最后补充一点：这正是为什么我们使用 Python 编程无关紧要的原因之一。尽管 Python 本身并非高性能语言，因为 CPU 从来不会成为性能瓶颈，它总能提前运行并将指令队列推送给 GPU 处理，正是这种 GPU 与 CPU 之间的解耦特性成为我们既能使用优雅的高级编程语言，又能充分发挥 GPU 性能的关键所在

OK，以上就是基准测试与性能分析的全部内容

4. Kernel fusion motivation

现在大家已经掌握了性能优化的全套工具，接下来我们将动手编写几个内核程序

记住 内核融合 这个概念，上图正是我们在上次讲座中展示的那张示意图。想象有个小工厂，每次执行运算时都需要把数据从仓库运到工厂，处理完再运回去，因此，如果我们不加思索地顺序执行一系列操作，就会反复支付数据在仓库与工厂之间来回搬运的高昂代价

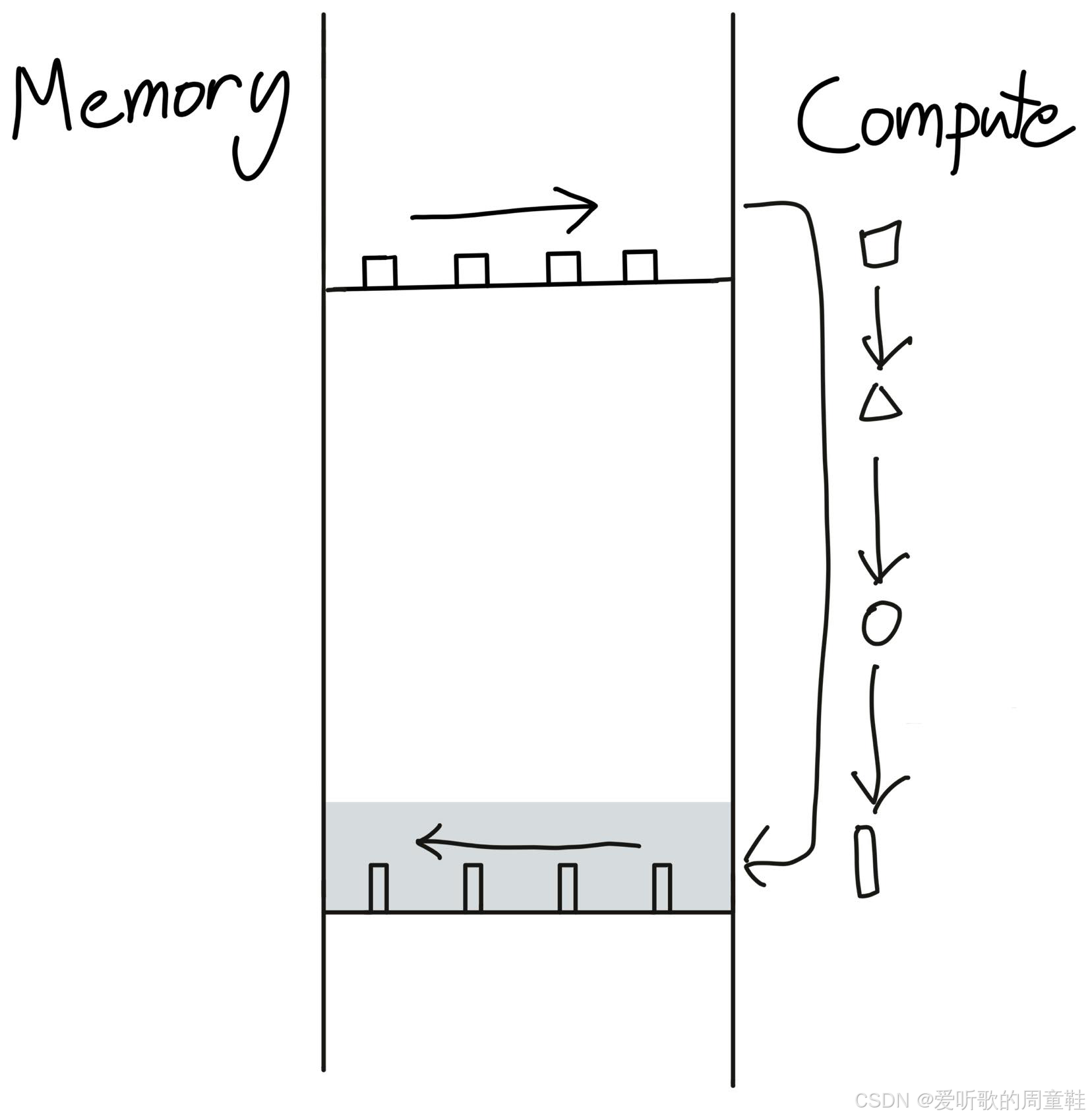
正确的做法是建立一个能一次性完成所有工序的工厂，这样就能避免重复支付这些搬运成本，这一点至关重要。

现在我们要实现 gelu 函数，并为其编写一个内核程序，我们将用几种不同的方式编写这个内核程序，然后观察不同实现方式对性能的影响。

PyTorch 实现的 gelu 函数代码如下所示：

def pytorch_gelu(x: torch.Tensor):
    # Use the tanh approximation to match our implementation
    return torch.nn.functional.gelu(x, approximate="tanh")

x = torch.tensor([1.])  # @inspect x
y1 = pytorch_gelu(x)  # @inspect y1

调用 torch.nn.functional.gelu 函数时，我们启用了 approximate="tanh" 参数，这是为了确保与接下来要实现的原始版本完全一致。这里我们不会直接乘以高斯分布的累积分布函数，而是采用了一个更易计算的近似公式，这就是 PyTorch 中的 gelu 实现

接下来，我们要用最原始的方法来实现它：

def manual_gelu(x: torch.Tensor):
    return 0.5 * x * (1 + torch.tanh(0.79788456 * (x + 0.044715 * x * x * x)))

y2 = manual_gelu(x)  # @inspect y2

当你看到这段代码时，肯定会说：这性能绝对高不了，手写实现的 gelu 函数中的魔法公式虽不精确，却是 gelu 的一个优秀近似，你可以查看相关资料或自行验证其正确性。

但实际操作时，你会发现其中涉及大量运算步骤，包括 tanh 双曲正切函数、输入值的幂运算、乘以常数系数、加减运算以及 0.5 与 x 的乘积操作，若将这些运算分散在多个不同的 CUDA 内核中执行，很可能会导致性能下降，根据内核融合（Fusion）的经验，此时我们理应形成这样的直觉判断，让我们验证这个判断是否成立

由此可见，这两者实际上是等效的，左上角显示二者的计算结果完全一致，我们可以通过随机高斯分布进行系统性验证

现在，让我们对两者进行基准测试

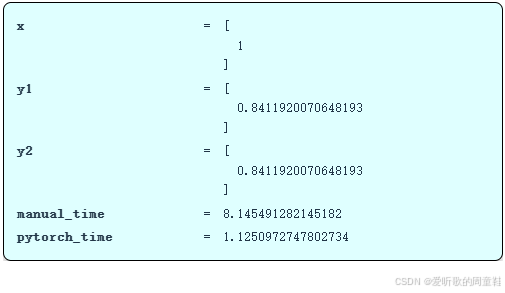
手动计算耗时 8.1 秒，这个数值确实非常庞大，而 PyTorch 的运算时间仅为 1.1 秒，经过内核融合的版本速度将显著提升，实际上快了八倍，这与编写简单内核相比差异巨大。当然，矩阵乘法运算可能仍是性能瓶颈，但如果能把耗时从 8 秒压缩到 1 秒，那可就太棒了，在接下来的课程环节中，我们将努力向 1.1 秒这个目标逼近

现在让我们深入底层看看实际运行情况，我们不需要查看 Nsight Systems 工具，因为真正需要了解的只是最核心的运行指标

正如我们之前提到的，手动实现的 gelu 会执行大量运算操作，这里会执行大量乘法运算，虽然运算已经向量化处理，但这里仍会触发多个 CUDA 内核的启动，注意右侧区域，at::native::BinaryFunctor<f... 这个 CUDA 内核被调用了三次，因为我们在此处进行了大量浮点乘法运算。此外还包含加法运算，还涉及双曲正切函数运算，而其中每一项运算都可能存在性能瓶颈，最终，这种操作方式会产生相当大的性能开销

现在，让我们用 PyTorch 的 gelu 实现同样的功能：

从上表可以看出，这样的实现确实非常理想，仅需启动单个 CUDA 内核，整个过程只需执行一次就能完全全部数据处理，这正是我们期望达到的效果，当然，这样的处理速度极快，因为仅需运行单个 CUDA 内核

这种实现方式非常理想，我们希望能深入理解这个 CUDA 内核的实现原理，根据你对编写高效 GPU 代码的了解程度，首先你可能会想到这个思路可行，PyTorch 团队肯定已经用最底层的语言实现了这个功能，我们也要采用同样的实现方式，我们不会采用最底层的实现方式，而是选择 C++ API，用 C++ 来编写这个 CUDA 内核

5. CUDA kernels

现在让我们开始动手编写自己的 CUDA 内核。那么具体要如何实现呢？我们要深入底层，用 C++ 重写整个实现

所谓 CUDA 实际上是指用于连接和编程 GPU 的 C 语言接口，基于我们描述的 GPU 逻辑模型，现在要编写其中的核心函数 f。当我们调用这个 CUDA 内核时，它会自动对向量或矩阵的所有元素执行函数 f，这样就能并行计算所有需要的运算

按照术语规范，我们将使用网格（grid）这一概念，它本质上是线程块（blocks）的集合体，可以这样理解：面对一个计算任务时，我们会将其分解为若干个子任务块，这些子任务块会被分配到多个计算块中执行。

以二维网格为例，每个计算块都拥有行坐标和列坐标两个维度标识，这种坐标体系在处理矩阵运算时尤为实用。每个计算块还具备特定的尺寸参数，表明这些计算块所包含的线程块数量具体是多少，因此这实际上定义了计算块的维度规模，而每个计算块内部又包含若干线程的集合，这个坐标体系确定了线程块的定位坐标，而每个线程又隶属于特定的线程块内部，这里存在一个层级化的结构体系，网格构成顶层结构，而线程则分布在网格内部运行

接下来，每个函数都将接收三个核心参数作为输入，分别是线程 threadIdx（标识所属线程块），线程块维度规格以及线程索引（标识线程在块内的具体位置），通过这些参数，我们就能确定当前线程在矩阵或向量中的具体坐标位置，从而执行相应的计算逻辑

在进入实际的 C++ 代码之前还有最后一点需要注意，调试 CUDA 时，务必设置环境变量 os.environ["CUDA_LAUNCH_BLOCKING"] = "1"，这样你才能正常调试 CUDA 内核，不过这会以牺牲运行时性能为代价，系统将能够返回详细的错误信息，若不启用该设置，在编写和调试 CUDA 代码时将会遇到极大困难

OK，下面是我们编写的 gelu 激活函数代码：

#include <math.h>
#include <torch/extension.h>
#include <c10/cuda/CUDAException.h>

__global__ void gelu_kernel(float* in, float* out, int num_elements) {
    // Get the index into the tensor
    int i = blockIdx.x * blockDim.x + threadIdx.x;

    if (i < num_elements) {  // To handle the case when n < numBlocks * blockDim
        // Do the actual computation
        out[i] = 0.5 * in[i] * (1.0 + tanh(0.79788456 * (in[i] + 0.044715 * in[i] * in[i] * in[i])));
    }
}

inline unsigned int cdiv(unsigned int a, unsigned int b) {
    // Compute ceil(a / b)
    return (a + b - 1) / b;
}

torch::Tensor gelu(torch::Tensor x) {
    TORCH_CHECK(x.device().is_cuda());
    TORCH_CHECK(x.is_contiguous());

    // Allocate empty tensor
    torch::Tensor y = torch::empty_like(x);

    // Determine grid (elements divided into blocks)
    int num_elements = x.numel();
    int block_size = 1024;  // Number of threads
    int num_blocks = cdiv(num_elements, block_size);

    // Launch the kernel
    gelu_kernel<<<num_blocks, block_size>>>(x.data_ptr<float>(), y.data_ptr<float>(), num_elements);
    C10_CUDA_KERNEL_LAUNCH_CHECK();  // Catch errors immediately

    return y;
}

现在让我们逐段解析，我们会详细解释每个部分的具体功能，这段代码的解析可能会成为我们整个讲解过程中最耗时的部分。当然，机器码分析除外，只要理解了这部分代码，其他所有模块的原理你都能触类旁通，那我们就放慢节奏，仔细梳理这段代码

这段代码主要包含两个核心部分，首先是 gelu_kernel 这段代码，这才是真正的核心计算内核：这部分负责具体的数学运算实现，这段代码会被发送到 GPU 执行计算任务，完成后将结果返回。而后面的 gelu 函数则是个封装层，这个封装层运行在 CPU 上，负责调度内核的启动，真正执行计算的内核则会被派到 GPU 上运行

那我们就从这个封装层开始，先看这个 gelu 函数：

torch::Tensor gelu(torch::Tensor x) {
    TORCH_CHECK(x.device().is_cuda());
    TORCH_CHECK(x.is_contiguous());

    // Allocate empty tensor
    torch::Tensor y = torch::empty_like(x);

    // Determine grid (elements divided into blocks)
    int num_elements = x.numel();
    int block_size = 1024;  // Number of threads
    int num_blocks = cdiv(num_elements, block_size);

    // Launch the kernel
    gelu_kernel<<<num_blocks, block_size>>>(x.data_ptr<float>(), y.data_ptr<float>(), num_elements);
    C10_CUDA_KERNEL_LAUNCH_CHECK();  // Catch errors immediately

    return y;
}

以 gelu 函数为起点，在 Triton 或 CUDA 代码中我们始终需要检查两个关键点：首先需要确保数据存放在 GPU 设备上，比如转换为 CUDA 张量，否则就会出问题，我们就无法在 GPU 上进行任何运算。其次（这点可能不太明显），我们需要检查确保数据在内存中是连续的，这意味着数据必须存储在连续的内存块中，因为当我们对数据进行索引操作时，会执行大量索引计算，而这些计算都基于数据存储在连续内存块这个前提，如果内存不连续，基本上就无法实现通用性的操作了

当我们计算 gelu 激活函数时，输入 x 经过处理后输出 y，因此我们需要分配输出空间，我们使用 torch::empty_like(x) 来创建与 x 形状相同的空张量，这样代码的意思是：请给我一个与 x 维度相同的输出张量空间，或者说指向该输出张量的指针，注意我们这里没有调用 zeros 初始化方法，这样可以省去额外的初始化操作，反正后续都会重新写入数据，这是个虽小但值得做的优化

接下来，在我们编写的所有代码中，都需要先确定网格 grid 的配置，那么总共有多少个元素呢？每个线程块的尺寸是多少？总共需要多少个线程块呢？当需要确定线程块数量时，我们会调用 cdiv 函数：

inline unsigned int cdiv(unsigned int a, unsigned int b) {
    // Compute ceil(a / b)
    return (a + b - 1) / b;
}

其核心计算逻辑是：用元素总数除以线程块尺寸，然后向上取整，因为只有向上取整才能确保那些无法被线程块尺寸整除的剩余元素也能被计算处理，因此我们选择向上取整而非向下取整，这些其实都是非常基础的线程管理操作

接着我们就可以直接启动内核了，于是 gelu 激活函数的内核便启动了

// Launch the kernel
gelu_kernel<<<num_blocks, block_size>>>(x.data_ptr<float>(), y.data_ptr<float>(), num_elements);

这里的尖括号 <<<...>>> 表示，前者是线程块数量，后者是每个线程块的尺寸，这些参数将被传入内核启动命令。接着我们会传入 x 和 y 的指针参数，实际上我们并不会直接传递 x 和 y 的数值，而是传入元素总数这个参数，这个参数用于计算内核的边界条件

现在让我们来看实际的内核代码：

__global__ void gelu_kernel(float* in, float* out, int num_elements) {
    // Get the index into the tensor
    int i = blockIdx.x * blockDim.x + threadIdx.x;

    if (i < num_elements) {  // To handle the case when n < numBlocks * blockDim
        // Do the actual computation
        out[i] = 0.5 * in[i] * (1.0 + tanh(0.79788456 * (in[i] + 0.044715 * in[i] * in[i] * in[i])));
    }
}

这里定义了一个全局内核函数 gelu_kernel，它接收输入输出指针参数以及元素总数 num_elements，其中 __global__ 是标识 CUDA 内核函数的关键字，那么这段代码具体在做什么呢？

没错，这个线程实际上只需要处理单个元素 i，但当前代码并没有将 i 作为输入参数传入，也没有明确告知 "你正在处理向量中第 i 个位置的元素"，因此需要自行计算当前线程所处理的位置索引

// Get the index into the tensor
int i = blockIdx.x * blockDim.x + threadIdx.x;

具体实现方式是：我们将获取当前线程块的索引，我们只有一个维度，所以是 blockIdx.x，也就是第一个坐标，然后乘以每个线程块的尺寸，也就是 blockDim.x，这样就得到了当前线程块内的起始位置，接着加上 threadIdx.x，这样既知道当前线程块的起始位置，又加上块内偏移量，最终得到全局坐标 i，这就是为了确定坐标所做的一些计算

if (i < num_elements) {  // To handle the case when n < numBlocks * blockDim

接下来的 if 判断代码也很关键，这种模式基本上在所有 CUDA 代码中都会出现，当然，这里没有做任何越界检查，所以实际操作是这样的：先获取当前坐标，然后检查这个坐标是否在有效范围内，确保只处理边界内的数据，而位于线程块末尾的部分线程会访问到内存越界区域，必须阻止这种操作。因此这里有个条件判断：当线程索引 i 小于元素总数 num_elements 时才执行计算，否则直接跳过。

现在我们有输入数据 in，我们会索引到第 i 个元素，然后像之前那样计算 gelu 激活值，最后将结果赋给 out 数据的第 i 个位置，这样就搞定了

由于这里处理的都是指针操作，我们其实不需要太关心底层的具体实现细节，核心逻辑就这么简单。这样我们就把现有的 CUDA 版 gelu 代码直接嵌入到 C++ 代码中，在 Python 环境里一站式编译成可调用模块，整个过程简洁又省心，完全不需要切换到命令行手动操作

现在我们已经完成了 CUDA 部分的定义，这样处理非常便捷，本质上这就是个编译过程，而且我们能在 Python 里直接调用它，我们将通过 C 语言绑定来调用这个模块

cuda_gelu = create_cuda_gelu() # @inspect cuda_gelu
x = manual_gelu # @inspect x

OK，CUDA 版 gelu 函数调用已完成，我们可以验证手动实现的 gelu 与 CUDA 版 gelu 是否一致，现在我们来对两者进行性能测试

if cuda_gelu is not None:
    check_equal(cuda_gelu, manual_gelu)

pytorch_time = benchmark("pytorch_gelu", run_operation1(dim=16384, operation=pytorch_gelu)) # @inspect pytorch_time
manual_time = benchmark("manual_gelu", run_operation1(dim=16384, operation=manual_gelu)) # @inspect manual_time
if cuda_gelu is not None:
    cuda_time = benchmark("cuda_gelu", run_operation1(dim=16384, operation=cuda_gelu)) # @inspect cuda_time 
    cuda_gelu_profile = profile("cuda_gelu", run_operation1(dim=16384, operation=cuda_gelu))

这里记录了 PyTorch 版本的运行耗时，和上次测试结果一致，耗时约为 1.1 秒，手动实现版本的耗时是 8.1 秒，和之前记录一样，现在重点来了，我们 CUDA 版本的耗时成功降低到了 1.8 秒，虽然还比不上 PyTorch 原生的实现速度，但已经非常接近 PyTorch 的运行耗时了，耗时从 8 秒优化到 1.8 秒，这个提升相当不错，毕竟刚才那段 C 语言代码写起来并不复杂

现在我们也开始进行性能分析：

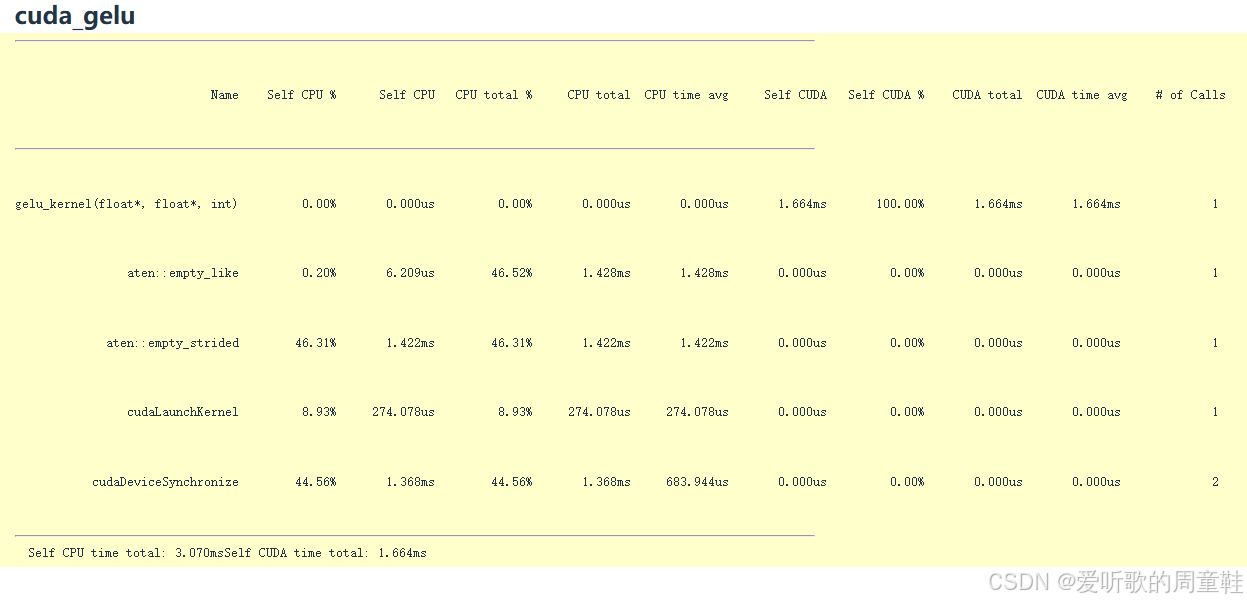
现在我们可以清楚地看到运行时的具体情况，这个内核函数名为 gelu_kernel，这段代码已被发送至 GPU 执行，接着它调用 empty_like 函数，这是初始化阶段，然后调用 empty_strided 函数，接着执行 CUDA 内核启动与设备同步操作，整个过程大致就是如此

注意看，这又是一个典型的 CUDA 内核独占 GPU 算力的场景，正如我们期望的那样，单个内核就能吃满 100% 的 GPU 运算时间，虽然还有进一步优化的空间，但至此我们已经彻底解决了内核融合的核心难题，我们成功将所有算子融合为一体，效果相当不错

这类逐元素运算用 CUDA 实现起来非常简单，如果你想实现某种新型非线性函数（比如自定义激活函数），完全可以自己动手写个 CUDA 内核。但更复杂的运算，比如规约操作就需要读取多个数值了，这类操作的实现会稍微复杂一些，例如 Flash Attention 的实现会稍微复杂些，但在作业中完成这个任务时，难度其实也没那么夸张

6. Triton kernels

OK，现在我们已经看到编写 CUDA kernels 的这个过程其实并不复杂，要是能用更优雅的 Python 抽象来编写 CUDA 内核就完美了，这正是 Triton 的用武之地，Triton 确实非常出色，它在这一点上做得恰到好处，你无需事无巨细地管理 GPU 的每个细节

6.1 Triton introduction

Triton 是 OpenAI 于 2021 年推出的领域专用语言，它显著降低了 GPU 编程的门槛，你可以用类 Python 的方式编写所有代码，完全无需再操心线程管理的问题，你只需专注于线程块的设计，而 Triton 能自动处理许多繁琐但可优化的底层细节

它能自动处理内存合并访问，请注意 DRAM 的突发传输模式（burst mode）会一次性读取四个相邻的存储单元值，因此务必确保内存访问模式以四个或更多相邻元素为单位进行连续读取，这些优化它会自动完成，它会自动合并这些访问

当需要管理多线程在流式多处理器 SM 内的共享内存写入时，系统会自动进行共享内存管理，在每个 SM 内部，线程的启停由系统自动管理，但跨 SM 的调度以及不同 SM 间的任务分配，仍需手动控制

编程模型要求开发者以 SM 为核心进行思考，而编译器会处理更多底层实现细节，Triton 的优势在于其性能表现，它往往能大幅超越许多 PyTorch 原生实现，这种方案几乎等同于直接编写 CUDA 代码，却仍保留着 Python 熟悉的开发环境

6.2 Triton gelu

另外一个被严重低估的优势是，正如下面要提到的 Triton 版本的 gelu 实现，整套系统完全基于 Python 实现，开发者可以逐行调试代码，整个过程异常顺畅

现在让我们逐步剖析一个 Triton 内核的实现，这次我们将使用 Triton 重新实现 gelu 激活函数：

def triton_gelu(x: torch.Tensor):
    assert x.is_cuda
    assert x.is_contiguous()

    # Allocate output tensor
    y = torch.empty_like(x)

    # Determine grid (elements divided into blocks)
    num_elements = x.numel()
    block_size = 1024  # Number of threads
    num_blocks = triton.cdiv(num_elements, block_size)

    triton_gelu_kernel[(num_blocks,)](x, y, num_elements, BLOCK_SIZE=block_size)

    return y

这段代码的结构设计尽可能与我们之前的实现保持了一致，这部分代码属于所谓的 CPU 端逻辑，这是封装 Triton 版 gelu 的包装代码。

该函数接收一个 PyTorch 张量 x 作为输入，并在开头设置了两条断言校验，这里我们再次使用 empty_like 方法分配了一个与输入尺寸相同的输出张量 y，其坐标计算模块与之前版本完全一致，甚至连内核启动的代码结构也如出一辙

这里通过 num_blocks 指定的线程块数量，而块大小参数则位于末尾，虽然没有直接放在方括号内，但本质上仍是将相同的信息传递给了内核

而下面的这段代码就是 Triton 版 gelu 内核的实现：

@triton.jit
def triton_gelu_kernel(x_ptr, y_ptr, num_elements, BLOCK_SIZE: tl.constexpr):
    # Input is at `x_ptr` and output is at `y_ptr`
    #     |        Block 0            |          Block 1          |      ...      |
    #                            BLOCK_SIZE                                 num_elements

    pid = tl.program_id(axis=0)
    block_start = pid * BLOCK_SIZE

    # Indices where this thread block should operate
    offsets = block_start + tl.arange(0, BLOCK_SIZE)

    # Handle boundary
    mask = offsets < num_elements

    # Read
    x = tl.load(x_ptr + offsets, mask=mask)

    # Approx gelu is 0.5 * x * (1 + tanh(sqrt(2/pi) * (x + 0.044715 * x^3)))
    # Compute (tl.tanh doesn't exist, use tanh(a) = (exp(2a) - 1) / (exp(2a) + 1)
    a = 0.79788456 * (x + 0.044715 * x * x * x)
    exp = tl.exp(2 * a)
    tanh = (exp - 1) / (exp + 1)
    y = 0.5 * x * (1 + tanh)

    # Store
    tl.store(y_ptr + offsets, y, mask=mask)

这段代码的功能与之前完全一致，只不过现在是用 Python 优雅地实现了，这里的核心逻辑时：所有输入数据都将通过 x 指针进行传递，y 指针指向输出向量，表示起始坐标，其中的 BLOCK_SIZE 参数决定了每个线程块的大小，而 num_elements 参数则决定了数组的终止边界

现在我们需要关注下面这段代码：

# Input is at `x_ptr` and output is at `y_ptr`
#     |        Block 0            |          Block 1          |      ...      |
#                            BLOCK_SIZE                                 num_elements

pid = tl.program_id(axis=0)
block_start = pid * BLOCK_SIZE

# Indices where this thread block should operate
offsets = block_start + tl.arange(0, BLOCK_SIZE)

这里正在计算索引值，我们之前用公式计算过 i 值，这里执行的其实是相同的索引计算，当前线程块的起始位置等于块 ID 乘以块大小，这样就能确定块起始索引，例如我们的线程块位于第一个块（Block 1）中，这样计算就会指向 Block 0 与 Block 1 的中间这个位置

接下来还需要确定我们在当前块内的具体位置，这就是偏移量 offset 的作用，现在请注意一个关键区别，由于不需要直接操作线程，这里不需要计算偏移量，我们现在是对计算块 Block 进行编程

这意味什么？实际上，我们的偏移量是一个向量值，而非单一数值，因为这本质上是要进行向量化运算，这些向量化操作将由不同的线程来并行处理。因此在这里，我们的偏移量是块的起始位置加上一个向量，即这个块大小范围内的偏移量，因此，我的偏移量是块内所有这些坐标点的集合，可以一次性处理

当然，如果处理到数据末尾时可能会越界，因此还需要一个掩码（mask）来处理向量边界外的数据。现在，我们将通过单次向量化操作一次性加载所有数据：

# Handle boundary
mask = offsets < num_elements

# Read
x = tl.load(x_ptr + offsets, mask=mask)

因此，x 指针加上偏移量就是我们要处理的数值范围，经过掩码处理后，这些值会被加载到 x 中，这是我们内部计算所需的临时向量存储空间

接下来，我们将用这个临时向量执行标准的 gelu 激活函数计算：

# Approx gelu is 0.5 * x * (1 + tanh(sqrt(2/pi) * (x + 0.044715 * x^3)))
# Compute (tl.tanh doesn't exist, use tanh(a) = (exp(2a) - 1) / (exp(2a) + 1)
a = 0.79788456 * (x + 0.044715 * x * x * x)
exp = tl.exp(2 * a)
tanh = (exp - 1) / (exp + 1)
y = 0.5 * x * (1 + tanh)

# Store
tl.store(y_ptr + offsets, y, mask=mask)

由于不涉及 tanh 函数，这部分需要手动计算实现，但这个公式经过验证，与当前使用的计算方式完全等效。最终，y 将按照上方公式计算得出，计算完成后，需要将结果写回到输出缓冲区（即输出向量）中

于是我们开始计算目标值，我们将临时计算得到的 y 值进行存储，这与之前的实现极其相似，但当前采用的是向量化版本，现在我们可以对整个数据块进行批量操作。因此，我们不再从单个线程的视角出发，而是切换到线程块的维度来思考，虽然视角不同，但核心逻辑并无本质差异，这些操作本质上大同小异

现在我们已经用 Triton 写好了 gelu 函数，最后还有一点需要注意，Triton 最厉害的地方在于它可以直接编译成 GPU 的底层机器码，当 Triton 编译器处理完成后，我们可以查看这种接近硬件的底层代码，也就是 PTX 汇编代码

    //// Generated by LLVM NVPTX Back-End//.version 8.4.target sm_90a.address_size 64
// .globl	triton_gelu_kernel      // -- Begin function triton_gelu_kernel
                                    // @triton_gelu_kernel
.visible .entry triton_gelu_kernel(
.param .u64 .ptr .global .align 1 triton_gelu_kernel_param_0,
.param .u64 .ptr .global .align 1 triton_gelu_kernel_param_1,
.param .u32 triton_gelu_kernel_param_2
).reqntid 128, 1, 1{
.reg .pred 	%p<5>;
.reg .b32 	%r<49>;
.reg .f32 	%f<113>;
.reg .b64 	%rd<8>;
.loc	1 552 0                         // lecture_06.py:552:0
$L__func_begin0:
.loc	1 552 0                         // lecture_06.py:552:0
// %bb.0:
ld.param.u64 	%rd5, [triton_gelu_kernel_param_0];
ld.param.u64 	%rd6, [triton_gelu_kernel_param_1];
$L__tmp0:
.loc	1 557 24                        // lecture_06.py:557:24
// begin inline asm
mov.u32 %r1, %ctaid.x;
// end inline asm
.loc	1 558 24                        // lecture_06.py:558:24
shl.b32 	%r42, %r1, 10;
ld.param.u32 	%r43, [triton_gelu_kernel_param_2];
.loc	1 561 41                        // lecture_06.py:561:41
mov.u32 	%r44, %tid.x;
shl.b32 	%r45, %r44, 2;
and.b32  	%r46, %r45, 508;
.loc	1 561 28                        // lecture_06.py:561:28
or.b32  	%r47, %r42, %r46;
or.b32  	%r48, %r47, 512;
.loc	1 564 21                        // lecture_06.py:564:21
setp.lt.s32 	%p1, %r47, %r43;
setp.lt.s32 	%p2, %r48, %r43;
.loc	1 567 24                        // lecture_06.py:567:24
mul.wide.s32 	%rd7, %r47, 4;
add.s64 	%rd1, %rd5, %rd7;
add.s64 	%rd2, %rd1, 2048;
.loc	1 567 16                        // lecture_06.py:567:16
// begin inline asm
mov.u32 %r2, 0x0;
mov.u32 %r3, 0x0;
mov.u32 %r4, 0x0;
mov.u32 %r5, 0x0;
@%p1 ld.global.v4.b32 { %r2, %r3, %r4, %r5 }, [ %rd1 + 0 ];
// end inline asm
mov.b32 	%f17, %r2;
mov.b32 	%f18, %r3;
mov.b32 	%f19, %r4;
mov.b32 	%f20, %r5;
// begin inline asm
mov.u32 %r6, 0x0;
mov.u32 %r7, 0x0;
mov.u32 %r8, 0x0;
mov.u32 %r9, 0x0;
@%p2 ld.global.v4.b32 { %r6, %r7, %r8, %r9 }, [ %rd2 + 0 ];
// end inline asm
mov.b32 	%f21, %r6;
mov.b32 	%f22, %r7;
mov.b32 	%f23, %r8;
mov.b32 	%f24, %r9;
.loc	1 571 37                        // lecture_06.py:571:37
mul.f32 	%f25, %f17, 0f3D372713;
mul.f32 	%f26, %f18, 0f3D372713;
mul.f32 	%f27, %f19, 0f3D372713;
mul.f32 	%f28, %f20, 0f3D372713;
mul.f32 	%f29, %f21, 0f3D372713;
mul.f32 	%f30, %f22, 0f3D372713;
mul.f32 	%f31, %f23, 0f3D372713;
mul.f32 	%f32, %f24, 0f3D372713;
.loc	1 571 41                        // lecture_06.py:571:41
mul.f32 	%f33, %f25, %f17;
mul.f32 	%f34, %f26, %f18;
mul.f32 	%f35, %f27, %f19;
mul.f32 	%f36, %f28, %f20;
mul.f32 	%f37, %f29, %f21;
mul.f32 	%f38, %f30, %f22;
mul.f32 	%f39, %f31, %f23;
mul.f32 	%f40, %f32, %f24;
.loc	1 571 26                        // lecture_06.py:571:26
fma.rn.f32 	%f41, %f33, %f17, %f17;
fma.rn.f32 	%f42, %f34, %f18, %f18;
fma.rn.f32 	%f43, %f35, %f19, %f19;
fma.rn.f32 	%f44, %f36, %f20, %f20;
fma.rn.f32 	%f45, %f37, %f21, %f21;
fma.rn.f32 	%f46, %f38, %f22, %f22;
fma.rn.f32 	%f47, %f39, %f23, %f23;
fma.rn.f32 	%f48, %f40, %f24, %f24;
.loc	1 571 22                        // lecture_06.py:571:22
mul.f32 	%f49, %f41, 0f3F4C422A;
mul.f32 	%f50, %f42, 0f3F4C422A;
mul.f32 	%f51, %f43, 0f3F4C422A;
mul.f32 	%f52, %f44, 0f3F4C422A;
mul.f32 	%f53, %f45, 0f3F4C422A;
mul.f32 	%f54, %f46, 0f3F4C422A;
mul.f32 	%f55, %f47, 0f3F4C422A;
mul.f32 	%f56, %f48, 0f3F4C422A;
.loc	1 572 21                        // lecture_06.py:572:21
fma.rn.f32 	%f57, %f41, 0f3F4C422A, %f49;
fma.rn.f32 	%f58, %f42, 0f3F4C422A, %f50;
fma.rn.f32 	%f59, %f43, 0f3F4C422A, %f51;
fma.rn.f32 	%f60, %f44, 0f3F4C422A, %f52;
fma.rn.f32 	%f61, %f45, 0f3F4C422A, %f53;
fma.rn.f32 	%f62, %f46, 0f3F4C422A, %f54;
fma.rn.f32 	%f63, %f47, 0f3F4C422A, %f55;
fma.rn.f32 	%f64, %f48, 0f3F4C422A, %f56;
.loc	1 572 17                        // lecture_06.py:572:17
mul.f32 	%f2, %f57, 0f3FB8AA3B;
// begin inline asm
ex2.approx.f32 %f1, %f2;
// end inline asm
mul.f32 	%f4, %f58, 0f3FB8AA3B;
// begin inline asm
ex2.approx.f32 %f3, %f4;
// end inline asm
mul.f32 	%f6, %f59, 0f3FB8AA3B;
// begin inline asm
ex2.approx.f32 %f5, %f6;
// end inline asm
mul.f32 	%f8, %f60, 0f3FB8AA3B;
// begin inline asm
ex2.approx.f32 %f7, %f8;
// end inline asm
mul.f32 	%f10, %f61, 0f3FB8AA3B;
// begin inline asm
ex2.approx.f32 %f9, %f10;
// end inline asm
mul.f32 	%f12, %f62, 0f3FB8AA3B;
// begin inline asm
ex2.approx.f32 %f11, %f12;
// end inline asm
mul.f32 	%f14, %f63, 0f3FB8AA3B;
// begin inline asm
ex2.approx.f32 %f13, %f14;
// end inline asm
mul.f32 	%f16, %f64, 0f3FB8AA3B;
// begin inline asm
ex2.approx.f32 %f15, %f16;
// end inline asm
.loc	1 573 18                        // lecture_06.py:573:18
add.f32 	%f65, %f1, 0fBF800000;
add.f32 	%f66, %f3, 0fBF800000;
add.f32 	%f67, %f5, 0fBF800000;
add.f32 	%f68, %f7, 0fBF800000;
add.f32 	%f69, %f9, 0fBF800000;
add.f32 	%f70, %f11, 0fBF800000;
add.f32 	%f71, %f13, 0fBF800000;
add.f32 	%f72, %f15, 0fBF800000;
.loc	1 573 30                        // lecture_06.py:573:30
add.f32 	%f73, %f1, 0f3F800000;
add.f32 	%f74, %f3, 0f3F800000;
add.f32 	%f75, %f5, 0f3F800000;
add.f32 	%f76, %f7, 0f3F800000;
add.f32 	%f77, %f9, 0f3F800000;
add.f32 	%f78, %f11, 0f3F800000;
add.f32 	%f79, %f13, 0f3F800000;
add.f32 	%f80, %f15, 0f3F800000;
.loc	1 573 24                        // lecture_06.py:573:24
mov.b32 	%r11, %f65;
mov.b32 	%r12, %f73;
// begin inline asm
div.full.f32 %r10, %r11, %r12;
// end inline asm
mov.b32 	%f81, %r10;
mov.b32 	%r14, %f66;
mov.b32 	%r15, %f74;
// begin inline asm
div.full.f32 %r13, %r14, %r15;
// end inline asm
mov.b32 	%f82, %r13;
mov.b32 	%r17, %f67;
mov.b32 	%r18, %f75;
// begin inline asm
div.full.f32 %r16, %r17, %r18;
// end inline asm
mov.b32 	%f83, %r16;
mov.b32 	%r20, %f68;
mov.b32 	%r21, %f76;
// begin inline asm
div.full.f32 %r19, %r20, %r21;
// end inline asm
mov.b32 	%f84, %r19;
mov.b32 	%r23, %f69;
mov.b32 	%r24, %f77;
// begin inline asm
div.full.f32 %r22, %r23, %r24;
// end inline asm
mov.b32 	%f85, %r22;
mov.b32 	%r26, %f70;
mov.b32 	%r27, %f78;
// begin inline asm
div.full.f32 %r25, %r26, %r27;
// end inline asm
mov.b32 	%f86, %r25;
mov.b32 	%r29, %f71;
mov.b32 	%r30, %f79;
// begin inline asm
div.full.f32 %r28, %r29, %r30;
// end inline asm
mov.b32 	%f87, %r28;
mov.b32 	%r32, %f72;
mov.b32 	%r33, %f80;
// begin inline asm
div.full.f32 %r31, %r32, %r33;
// end inline asm
mov.b32 	%f88, %r31;
.loc	1 574 14                        // lecture_06.py:574:14
mul.f32 	%f89, %f17, 0f3F000000;
mul.f32 	%f90, %f18, 0f3F000000;
mul.f32 	%f91, %f19, 0f3F000000;
mul.f32 	%f92, %f20, 0f3F000000;
mul.f32 	%f93, %f21, 0f3F000000;
mul.f32 	%f94, %f22, 0f3F000000;
mul.f32 	%f95, %f23, 0f3F000000;
mul.f32 	%f96, %f24, 0f3F000000;
.loc	1 574 23                        // lecture_06.py:574:23
add.f32 	%f97, %f81, 0f3F800000;
add.f32 	%f98, %f82, 0f3F800000;
add.f32 	%f99, %f83, 0f3F800000;
add.f32 	%f100, %f84, 0f3F800000;
add.f32 	%f101, %f85, 0f3F800000;
add.f32 	%f102, %f86, 0f3F800000;
add.f32 	%f103, %f87, 0f3F800000;
add.f32 	%f104, %f88, 0f3F800000;
.loc	1 574 19                        // lecture_06.py:574:19
mul.f32 	%f105, %f89, %f97;
mul.f32 	%f106, %f90, %f98;
mul.f32 	%f107, %f91, %f99;
mul.f32 	%f108, %f92, %f100;
mul.f32 	%f109, %f93, %f101;
mul.f32 	%f110, %f94, %f102;
mul.f32 	%f111, %f95, %f103;
mul.f32 	%f112, %f96, %f104;
.loc	1 577 21                        // lecture_06.py:577:21
add.s64 	%rd3, %rd6, %rd7;
add.s64 	%rd4, %rd3, 2048;
.loc	1 577 30                        // lecture_06.py:577:30
mov.b32 	%r34, %f105;
mov.b32 	%r35, %f106;
mov.b32 	%r36, %f107;
mov.b32 	%r37, %f108;
// begin inline asm
@%p1 st.global.v4.b32 [ %rd3 + 0 ], { %r34, %r35, %r36, %r37 };
// end inline asm
mov.b32 	%r38, %f109;
mov.b32 	%r39, %f110;
mov.b32 	%r40, %f111;
mov.b32 	%r41, %f112;
// begin inline asm
@%p2 st.global.v4.b32 [ %rd4 + 0 ], { %r38, %r39, %r40, %r41 };
// end inline asm
.loc	1 577 4                         // lecture_06.py:577:4
ret;
$L__tmp1:$L__func_end0:
                                    // -- End function
}
.file	1 "/home/c-thashim/2025/spring2025-lectures/lecture_06.py"
.section	.debug_abbrev
{
.b8 1                                   // Abbreviation Code.b8 17                                  // DW_TAG_compile_unit.b8 0                                   // DW_CHILDREN_no.b8 37                                  // DW_AT_producer.b8 8                                   // DW_FORM_string.b8 19                                  // DW_AT_language.b8 5                                   // DW_FORM_data2.b8 3                                   // DW_AT_name.b8 8                                   // DW_FORM_string.b8 16                                  // DW_AT_stmt_list.b8 6                                   // DW_FORM_data4.b8 27                                  // DW_AT_comp_dir.b8 8                                   // DW_FORM_string.b8 0                                   // EOM(1).b8 0                                   // EOM(2).b8 0                                   // EOM(3)
}
.section	.debug_info
{
.b32 76                                 // Length of Unit.b8 2                                   // DWARF version number.b8 0.b32 .debug_abbrev                      // Offset Into Abbrev. Section.b8 8                                   // Address Size (in bytes).b8 1                                   // Abbrev [1] 0xb:0x45 DW_TAG_compile_unit.b8 116                                 // DW_AT_producer.b8 114.b8 105.b8 116.b8 111.b8 110.b8 0.b8 2                                   // DW_AT_language.b8 0.b8 108                                 // DW_AT_name.b8 101.b8 99.b8 116.b8 117.b8 114.b8 101.b8 95.b8 48.b8 54.b8 46.b8 112.b8 121.b8 0.b32 .debug_line                        // DW_AT_stmt_list.b8 47                                  // DW_AT_comp_dir.b8 104.b8 111.b8 109.b8 101.b8 47.b8 99.b8 45.b8 116.b8 104.b8 97.b8 115.b8 104.b8 105.b8 109.b8 47.b8 50.b8 48.b8 50.b8 53.b8 47.b8 115.b8 112.b8 114.b8 105.b8 110.b8 103.b8 50.b8 48.b8 50.b8 53.b8 45.b8 108.b8 101.b8 99.b8 116.b8 117.b8 114.b8 101.b8 115.b8 0
}
.section	.debug_macinfo	{	}

你能直观看到 GPU 在单个线程层面的实际工作机制，上面就是用 Triton 实现的 gelu 激活函数内核，这段代码是由 Triton 编译器自动生成的

首先它会执行一些最基础的操作：

.reg .pred 	%p<5>;
.reg .b32 	%r<49>;
.reg .f32 	%f<113>;
.reg .b64 	%rd<8>;

那么它在这里具体执行什么操作呢？代码正在声明需要存储一些中间值，这里需要存储中间计算结果，其中的 .b 实际上表示无类型数据，本质上相当于字节（byte）类型，我们需要 32 位长度的比特数据，需要用于计算的浮点数，记为 f，此外还需要另一种 64 位的寄存器，这属于另一套寄存器组，我们需要所有这些寄存器来存储临时计算结果

.loc	1 552 0                         // lecture_06.py:552:0
$L__func_begin0:
.loc	1 552 0                         // lecture_06.py:552:0
// %bb.0:
ld.param.u64 	%rd5, [triton_gelu_kernel_param_0];
ld.param.u64 	%rd6, [triton_gelu_kernel_param_1];

这部分代码负责加载函数的各个参数，像 x 指针和 y 指针这样的参数就是在这里加载的

$L__tmp0:
.loc	1 557 24                        // lecture_06.py:557:24
// begin inline asm
mov.u32 %r1, %ctaid.x;
// end inline asm
.loc	1 558 24                        // lecture_06.py:558:24
shl.b32 	%r42, %r1, 10;
ld.param.u32 	%r43, [triton_gelu_kernel_param_2];
.loc	1 561 41                        // lecture_06.py:561:41
mov.u32 	%r44, %tid.x;
shl.b32 	%r45, %r44, 2;
and.b32  	%r46, %r45, 508;
.loc	1 561 28                        // lecture_06.py:561:28
or.b32  	%r47, %r42, %r46;
or.b32  	%r48, %r47, 512;
.loc	1 564 21                        // lecture_06.py:564:21
setp.lt.s32 	%p1, %r47, %r43;
setp.lt.s32 	%p2, %r48, %r43;
.loc	1 567 24                        // lecture_06.py:567:24
mul.wide.s32 	%rd7, %r47, 4;
add.s64 	%rd1, %rd5, %rd7;
add.s64 	%rd2, %rd1, 2048;
.loc	1 567 16                        // lecture_06.py:567:16
// begin inline asm
mov.u32 %r2, 0x0;
mov.u32 %r3, 0x0;
mov.u32 %r4, 0x0;
mov.u32 %r5, 0x0;
@%p1 ld.global.v4.b32 { %r2, %r3, %r4, %r5 }, [ %rd1 + 0 ];

从上面这里开始，我们将计算 Triton 内核的坐标偏移量，接着往下执行，直到遇到 ld.global.v4,b32 这个全局加载指令，这段代码的作用是从 x 指针加载数据到临时寄存器中，这段代码的意思是通过 rd1 寄存器中的内存地址，将数据加载到 r2、r3、r4、r5 寄存器中，一次性加载了四个数据，这种设计巧妙地实现了内存访问的合并操作，既然能免费获取四个数值，我们就一次性处理这四个值，毕竟已经拿到手了

接着往下看，你会看到完全相同的操作又重复了一次：

mov.b32 	%f17, %r2;
mov.b32 	%f18, %r3;
mov.b32 	%f19, %r4;
mov.b32 	%f20, %r5;
// begin inline asm
mov.u32 %r6, 0x0;
mov.u32 %r7, 0x0;
mov.u32 %r8, 0x0;
mov.u32 %r9, 0x0;
@%p2 ld.global.v4.b32 { %r6, %r7, %r8, %r9 }, [ %rd2 + 0 ];

接下来你会看到浮点运算指令 mul.f32 开始执行：

mul.f32 	%f25, %f17, 0f3D372713;
mul.f32 	%f26, %f18, 0f3D372713;
mul.f32 	%f27, %f19, 0f3D372713;
mul.f32 	%f28, %f20, 0f3D372713;
mul.f32 	%f29, %f21, 0f3D372713;
mul.f32 	%f30, %f22, 0f3D372713;
mul.f32 	%f31, %f23, 0f3D372713;
mul.f32 	%f32, %f24, 0f3D372713;

这些指令逐步完成 tanh 函数的计算过程，这里我们就不逐项解释了，可以看到它在乘以一个常数，并通过多次自乘实现了 x 的三次方运算

接下来程序会计算 2^x，但我们需要的是 e^x，于是它会乘以 log 2 来转换指数底数：

mul.f32 	%f2, %f57, 0f3FB8AA3B;
// begin inline asm
ex2.approx.f32 %f1, %f2;
// end inline asm

你能清晰看到 GPU 为获得最终结果所执行的所有具体操作步骤，每个环节都明明白白地展现出来，我们就直接跳到最终部分，中间的全都是必须执行的浮点运算操作

// begin inline asm
@%p2 st.global.v4.b32 [ %rd4 + 0 ], { %r38, %r39, %r40, %r41 };
// end inline asm

最后阶段，程序会将寄存器 r38 到 r41 中的计算结果存入到 rd4 中，这个内存地址正好是我们输出数据的存储位置，这就是底层实际发生的运行过程

可以看到，每个线程都在同时处理四个数值，这些运算的临时存储都放在寄存器里，这种超高速存储单元就紧邻着运算核心，显然，光是看这段代码的结构就能判断，它的执行速度应该相当快

OK，以上就是 PTX 代码的分析过程，我们可以逐步查看它在各类运算中的具体行为

不过现在，让我们回到正题，实际跑个性能测试：

manual_time = benchmark("manual_gelu", run_operation1(dim=16384, operation=manual_gelu)) # @inspect manual_time
pytorch_time = benchmark("pytorch_gelu", run_operation1(dim=16384, operation=pytorch_gelu)) # @inspect pytorch_time
cuda_time = benchmark("cuda_gelu", run_operation1(dim=16384, operation=create_cuda_gelu())) # @inspect cuda_time
triton_time = benchmark("triton_gelu", run_operation1(dim=16384, operation=triton_gelu)) # @inspect triton_time

triton_gelu_profile = profile("triton_gelu", run_operation1(dim=16384, operation=triton_gelu))

测试结果显示，手动实现的 gelu 耗时 8.1 秒，PyTorch 原生实现仅需 1.1 秒，CUDA 版本 1.84 秒，而 Triton 实现则为 1.848 秒，虽然性能没有提升，但用 Triton 编写代码确实轻松多了

我们用 Python 编写代码，只需考虑线程块划分，还能实现向量化加法运算，当处理更复杂的运算时，Triton 能自动帮你搞定大部分内存管理的工作，确实相当好用

性能分析再次显示：整个 GPU 运算时间都被单个内核启动所占用，这非常理想，而且正好适用于 Triton 内核

7. Pytorch compilation

接下来要重点讨论的是 torch.compile 这个功能，当然，手写 CUDA 内核很酷也很有成就感，但我们或许不必如此大费周章，我们当前实现的功能其实相当基础，我们只是将 x^3 和指数运算这些操作全部塞进同一个 CUDA 内核，或许我们不用大动干戈就能实现这个效果

我们已经展示了多种优化方法，但最后要介绍的是 torch.compile，它能将未优化的 PyTorch 代码自动转换为更高效的版本，这个工具会自动尝试进行内核融合等优化操作

compiled_gelu = torch.compile(manual_gelu)

这个经过编译的 gelu 函数在实际输出结果上与原版完全等效，现在让我们来看看运行时间的对比：

虽然运行时间存在些许波动，但整体性能数据基本持平，手动实现耗时 8.1 秒，PyTorch 耗时 1.1 秒，CUDA 版本 1.8 秒，而 torch.compile 则取得了 1.47 秒的成绩。由此可见，现代即时编译器的性能已经相当出色，它能自动实现算子融合等优化，开发者几乎无需手动干预

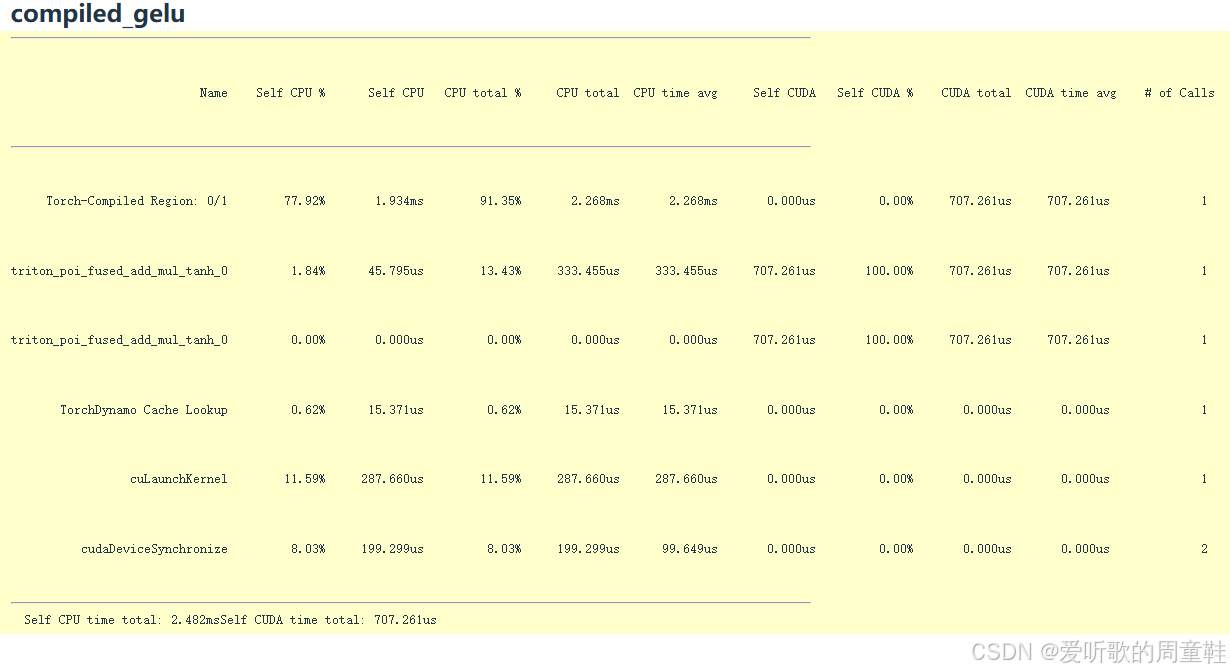
深入底层观察就会发现，核心优化机制其实万变不离其宗，这段代码实现了加法、乘法和 tanh 激活函数融合的 Triton 内核，实际上系统在底层自动生成的 Triton 代码，其优化效果比我们手动编写的版本还要略胜一筹，因此 torch.compile 确实是个非常实用的工具

8. Triton softmax

最后，我们快速过下最后一个 Triton 的示例，这个示例或许对大家完成作业二中的 softmax 实现会有所启发

与之前单纯处理逐元素运算不同，这次我们要实现更复杂的操作，这种逐元素运算确实简单，因为只需独立处理每个数据点，完全不需要考虑运算间的复杂关联

现在让我们实现 softmax 函数，这个运算需要执行归约操作，即对所有元素进行求和运算，具体该如何实现呢？我们的目标是对矩阵中的每一行进行归一化处理，而我们希望以更高效的方法实现这一目标

显然，直接实现的原始版本运行效率会非常低下，现在我们将着手编写 Triton 内核代码：

def triton_softmax(x: torch.Tensor):
    # Allocate output tensor
    y = torch.empty_like(x)

    # Determine grid
    M, N = x.shape                          # Number of rows x number of columns
    block_size = triton.next_power_of_2(N)  # Each block contains all the columns
    num_blocks = M                          # Each block is a row

    # Launch kernel
    triton_softmax_kernel[(M,)](
        x_ptr=x, y_ptr=y,
        x_row_stride=x.stride(0), y_row_stride=y.stride(0),
        num_cols=N, BLOCK_SIZE=block_size
    )

    return y

现在我们需要实现一个 softmax 函数，我们需要对矩阵的每一行进行归一化处理，假设这些矩阵的规模都比较小，我们只需针对小规模矩阵编写内核，在这种情况下，应该如何设计线程块结构呢？

或许我们可以考虑将网格的维度直接设置为行数，这样每个流式多处理器 SM 将负责处理单独一行数据，这确实是最优的实现方案，因为当整行数据能完整载入单个 SM 时，我们就能在 SM 内部完成行内求和运算，最后再进行除法操作，这样非常理想

因此，这将作为我们当前这个最基础版 softmax 核函数的简单设计方案，我们将把每行数据分配给一个线程块处理，因此块大小应该设置为列数，并预留少量缓冲空间以确保能容纳所有列数据

这里使用 triton.next_power_of_2(N) 函数处理列数 n，这种取二次幂的填充方式非常实用。接下来，我们会将每行数据分配给一个线程块来处理，因此，线程块的总数就等于数据的行数

然后我们实现了标准的 Triton softmax 核函数，其编写方式完全符合常规实现规范：

@triton.jit
def triton_softmax_kernel(x_ptr, y_ptr, x_row_stride, y_row_stride, num_cols, BLOCK_SIZE: tl.constexpr):
    assert num_cols <= BLOCK_SIZE

    # Process each row independently
    row_idx = tl.program_id(0)
    col_offsets = tl.arange(0, BLOCK_SIZE)

    # Read from global memory
    x_start_ptr = x_ptr + row_idx * x_row_stride
    x_ptrs = x_start_ptr + col_offsets
    x_row = tl.load(x_ptrs, mask=col_offsets < num_cols, other=float("-inf"))

    # Compute
    x_row = x_row - tl.max(x_row, axis=0)
    numerator = tl.exp(x_row)
    denominator = tl.sum(numerator, axis=0)
    y_row = numerator / denominator

    # Write back to global memory
    y_start_ptr = y_ptr + row_idx * y_row_stride
    y_ptrs = y_start_ptr + col_offsets
    tl.store(y_ptrs, y_row, mask=col_offsets < num_cols)

现在我们要处理的是矩阵而非向量，我们持有 x 和 y 指针，需要获取矩阵的步长 strides，这样就能确定当前处理的是哪一行数据，可以获取列偏移量，这段代码的实现逻辑与之前保持一致。实际上，获取行偏移量更简单，因为每个线程块正好对应一行数据，接下来要做的，本质上还是同样的处理逻辑，我们会将每行数据加载到流式多处理器 SM 的本地内存中，然后执行计算

整个过程与实现 softmax 函数的处理方式完全一致，获取当前行数据后，先减去最大值，再做指数运算，求和后执行除法，这样就能得到经过 softmax 归一化的行数据，最后将其写回全局内存，整个过程简洁明了

当计算任务恰好适配 SM 的处理能力时，编写 Triton 代码的感觉就像写普通 Python 代码一样自然，只需额外处理数据加载/存储操作，并注意线程块的分布情况，这样操作起来其实很简单

回到 Triton 的话题上来，这样我们就能直观比较各段代码的执行效率了：

manual_time = benchmark("manual_softmax", run_operation1(dim=16384, operation=manual_softmax)) # @inspect manual_time
compiled_time = benchmark("compiled_softmax", run_operation1(dim=16384, operation=compiled_softmax)) # @inspect compiled_time
pytorch_time = benchmark("pytorch_softmax", run_operation1(dim=16384, operation=pytorch_softmax)) # @inspect pytorch_time
triton_time = benchmark("triton_softmax", run_operation1(dim=16384, operation=triton_softmax)) # @inspect triton_time

我们再整体梳理一下确保大家理解，各方案耗时分别为：手动实现 3.7 秒，torch.compile 编译耗时 1.3 秒，PyTorch 执行 1.5 秒，Triton 实现 1.9 秒，可见 Triton 版本仍有优化空间，torch.compile 在某些情况下能超越原生 PyTorch 实现的性能，特别是当它掌握了运算张量的具体形状和尺寸信息时

最后我们可以通过性能分析工具查看具体数据：

手动实现的 softmax 在这里表现相当糟糕，可以看到各种混乱的操作在四处发生，可以看到各种运算操作正在执行，当前代码中存在 x、最大值计算和求和运算，由于我们采用了最基础的实现方式，导致内存读写操作遍布各处

编译后的 softmax 将融合为单个高效运算单元，执行速度显著提升

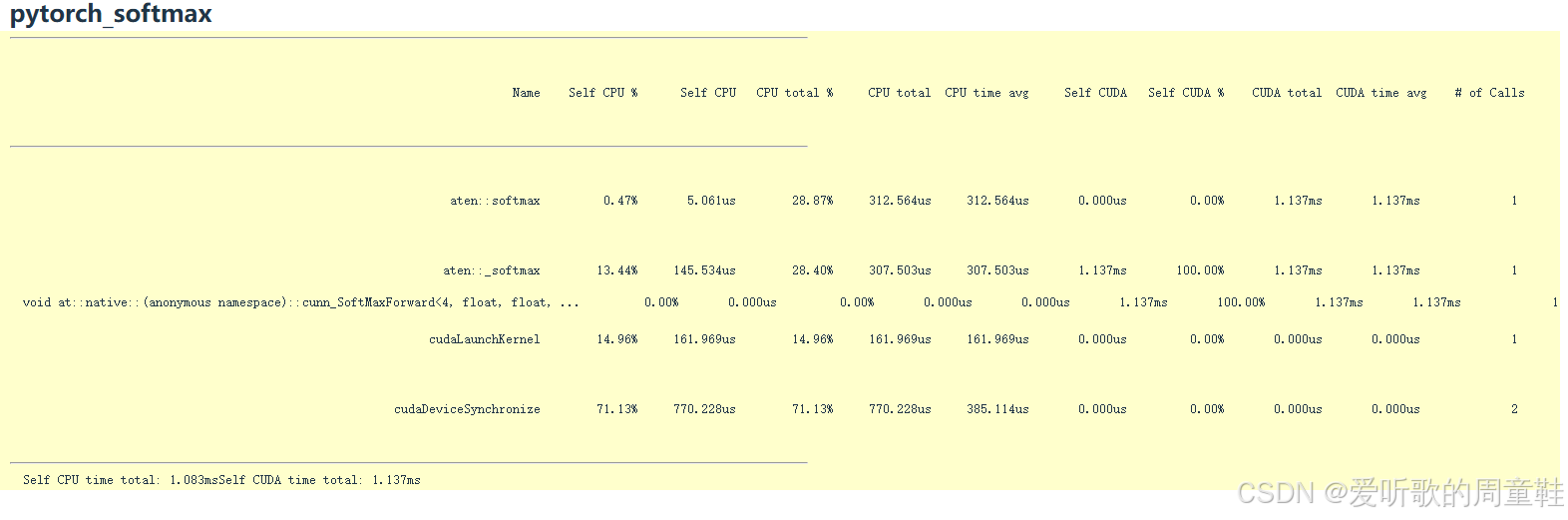
PyTorch 的 softmax 同样只需调用一个 CUDA 内核

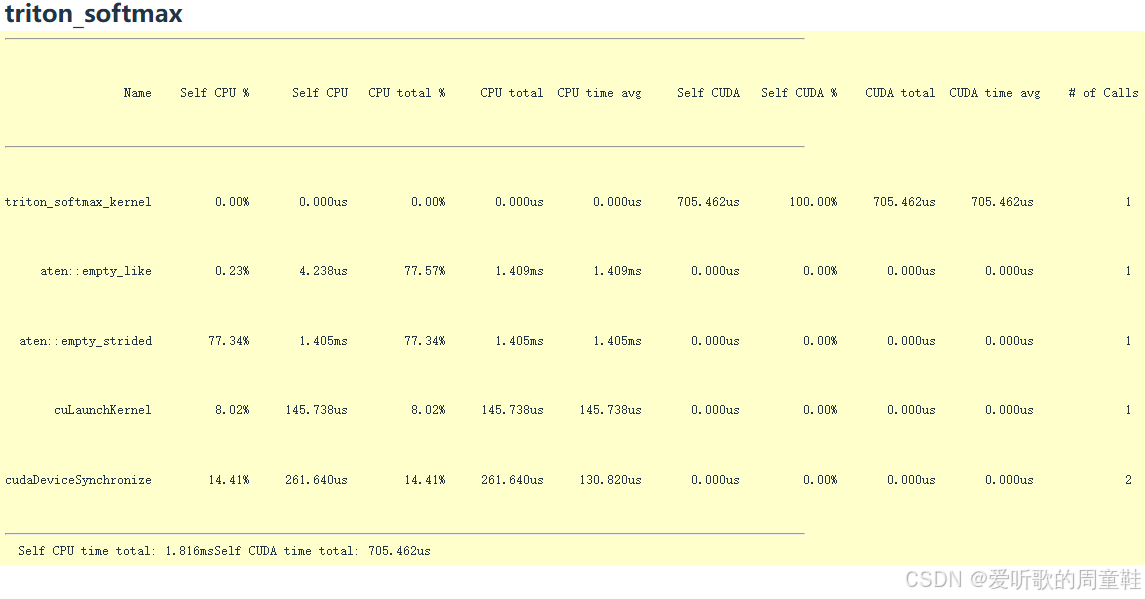
我们的 Triton 版 softmax 实现也是如此，我们实现了优雅的 Triton 版 softmax 内核，它将所有运算融合为单个高效内核

OK，后面的 PTX 代码我们就不展开讲解了，希望通过上面这些内容，大家能对加速语言模型的底层 GPU 编程有直观认识

9. Summary

最后，我们来对本次课程所讲的内容做一个回顾，希望大家能够掌握到其中的要点

本次课程我们主要探讨了编写高效 GPU 代码时，编程模型与硬件实现之间的鸿沟。虽然我们通常使用 PyTorch、Triton 或 PTX 这样的高级抽象来开发 GPU 程序，但这些抽象层往往掩盖了底层的执行机制---包括线程调度、内存层次结构、以及 warp 执行等细节。正是这种抽象与硬件之间的差距，导致了许多"性能之谜"：代码逻辑正确但性能却远低于预期。

为了理解这些性能现象，本次课程分别从以下三个层次入手：

• 1. Benchmarking --- 通过实验观察代码在不同规模下的扩展行为；
• 2. Profiling --- 利用工具分析 PyTorch 或 CUDA 内部的 kernel 调度与内存瓶颈；
• 3. PTX 级分析 ------ 通过查看汇编理解编译器如何生成底层指令。

我们还实现了同一函数（以 gelu、softmax 为例）的五种方式：从最原始的 Python 手写实现，到 PyTorch 自带算子、torch.compile 编译优化、CUDA 原生内核，再到 Triton DSL。

以典型算子为例：

• GeLU 属于逐元素计算，瓶颈在内存访问；
• Softmax 需要行内归一化，受同步与带宽限制；
• MatMul 则是计算密集型操作，主要受限于共享内存和寄存器复用。

整节课的核心原则是：组织计算以最小化读写开销，这背后延伸出两个关键优化思想：

• Kernel Fusion：将多个计算阶段融合为一个内核，减少中间结果的存取；
• Tiling（分块）：通过在共享内存中复用数据提升局部性与吞吐率。

最后，我们还聊到了自动化编译器的发展，如 Triton 与 torch.compile，它们正不断缩小高层框架与底层硬件性能之间的差距。未来，更多的性能优化将由编译器自动完成，而我们需要保留的是对 GPU 硬件和计算组织的深刻理解

如果大家还想进一步深入了解如何编写 GPU 高性能代码，下面有一些资料你可能会用到

• Horace He's Blog: Brrr --- An Intuitive Intro to GPU Programming
• CUDA MODE Lecture Series:
  • Lecture 1: How to Profile CUDA Kernels in PyTorch
  • Lecture 2: Chapters 1--3 of Programming Massively Parallel Processors
  • Lecture 3: Getting Started with CUDA for Python Programmers
  • Lecture 4: Compute and Memory Basics
  • Lecture 8: CUDA Performance Checklist
• HetSys GPU Programming Course:
  • Lecture 1: Programming Heterogeneous Computing Systems with GPUs
  • Lecture 2: SIMD Processing and GPUs
  • Lecture 3: GPU Software Hierarchy
  • Lecture 4: GPU Memory Hierarchy
  • Lecture 5: GPU Performance Considerations
• More Resources:
  • A100 GPU with NVIDIA Ampere Architecture
  • NVIDIA Deep Learning Performance Guide
  • GPU Puzzles (Interactive Learning)
  • Triton: A Language for Efficient Deep Learning
  • PyTorch 2.0 Acceleration: Operator Fusion & Code Generation

OK，以上就是本次讲座的全部内容了

结语

本讲我们主要讲解了如何编写高性能 GPU 代码，涵盖执行/存储模型回顾、基准测试与性能剖析方法、内核融合思想，以及用 CUDA、Triton 与 torch.compile 落地优化的完整路径。

在 GPU 基础回顾 小节中，我们从 SM/warp 的并行执行机制与分层内存结构出发，强调"高算术强度"与"同块内数据交互"的重要性：线程块内可用共享内存与寄存器实现高速协同，而跨块通信代价高，应尽量将需要交互的数据约束在同一块中；同时指出 waves/warp 负载均衡 与 块数远大于 SM 数 的配置对吞吐至关重要。

在 基准测试与性能剖析 小节，我们给出了可复用的基准测试规范（预热 + torch.cuda.synchronize()），并用 MLP、矩阵乘法等示例展示了规模与耗时的线性关系。随后通过 PyTorch Profiler 与 Nsight Systems 深入到内核级时间线，直观呈现 CPU 负责排队投递 CUDA 内核、GPU 异步执行的流水化关系，以及日志打印等 CPU 同步点如何"拉低"并行效率的真实场景。

在 内核融合动机 小节，我们以 gelu 为载体对比了"手写逐元素算子（多核多次访存）"与"融合后单核一次访存"的巨大差异，得到关键原则：减少全局内存读写、合并访存回合数 。随后我们分别 手写 CUDA 内核 与 Triton 内核 实现 gelu，说明索引计算、边界掩码与块粒度向量化读取的通用模式，并下潜到 PTX 观察寄存器分配、ld.global.v4 合并加载与指数/乘加序列

在后面我们还系统对比了三种实现：

• CUDA：控制力最强、性能可逼近库内核；
• Triton：以"块"为编程单元，自动做合并访存与部分内存管理，保持高可读性与可调优空间；
• torch.compile：对原生 PyTorch 自动做算子融合与形状专门化，很多场景可"零改动"获得与手写内核相近甚至更优的性能。

结论是：先用基准与剖析找瓶颈 → 优先尝试 torch.compile → 再用 Triton/CUDA 针对性攻克重核或特殊算子

在最后的 Triton 版 softmax 小节，我们给出了"一行一个块 、块内完成行内归约（max/sum）与归一化"的高效设计，对比了手写/编译/PyTorch/Triton 各方案的耗时与剖析视图，再次印证了将数据就地留在 SM 内完成复合计算是吞吐最优解。

整个讲解非常通俗易懂，大家感兴趣的可以看看

下节课我们将详细讨论跨设备并行化，敬请期待🤗

参考

• https://stanford-cs336.github.io/spring2025
• https://www.youtube.com/playlist?list=PLoROMvodv4rOY23Y0BoGoBGgQ1zmU_MT_
• https://github.com/stanford-cs336/spring2025-lectures
• https://stanford-cs336.github.io/spring2025-lectures/?trace=var/traces/lecture_06.json