在图论、网络分析乃至图神经网络(GNN)中,邻接矩阵(Adjacency Matrix) 是描述图结构最基础也最强大的工具之一。但你是否曾好奇:邻接矩阵的平方、立方,甚至 k 次幂,到底代表了什么?
今天,我们就来揭开这个看似抽象的数学操作背后的直观含义 ------它其实是在"数路径"!
📌 一、什么是邻接矩阵?
假设我们有一个包含 n 个节点的图 G = (V, E) ,其邻接矩阵 A 是一个 n x n 的矩阵,定义如下:

如果是带权图,A_{ij} 可以是边的权重;如果是无向图,A 是对称矩阵。
例如,一个简单的有向图:
1 → 2 → 3其邻接矩阵为:
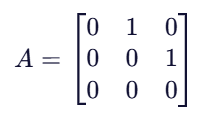
🔢 二、邻接矩阵的平方:长度为 2 的路径数量
现在,我们计算 A^2 = A * A 。
矩阵乘法告诉我们:
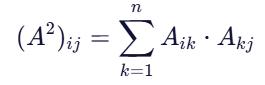
这个求和项只有在 存在某个中间节点 k,使得 i -> k 和 k -> j 都有边时,才会为 1。
换句话说:
(A^2)_{ij} 表示从节点 i 到节点 j 的长度为 2 的路径数量!
✅ 举例验证
用上面的例子:
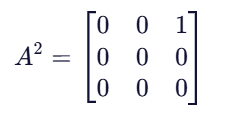
- (A^2)_{13} = 1 :确实存在路径 1 -> 2 -> 3
- 其他位置为 0:没有其他长度为 2 的路径
完美吻合!
🧮 三、推广:邻接矩阵的 k 次幂
通过数学归纳法可以证明:
定理 :邻接矩阵 A 的 k 次幂 A^k 中,元素 (A^k)_{ij} 等于从节点 i 到节点 j 的长度为 k的路径数量。
📌 注意:
- 这里的"路径"允许重复节点(即 walk,而非 simple path)
- 如果图是无权的,结果是整数(路径条数)
- 如果图是带权的,结果是所有长度为 k 的路径的权重乘积之和
🌐 四、直观理解:信息如何在图上传播?
邻接矩阵的幂次还有一个非常重要的动态视角:
- A^1:一步能到达哪里?
- A^2:两步能到达哪里?
- A^k:k 步能到达哪里?
这正是图神经网络(GNN) 中"消息传递"的数学基础!
例如,在 GCN 中,节点通过聚合邻居信息来更新自身表示。经过 k 层 GCN,每个节点实际上"看到"了距离它 k 跳以内的所有邻居------这与 A^k 的作用高度一致。
💡 邻接矩阵的幂 = 信息在图上扩散的范围
🧪 五、实际应用举例
1. 社交网络中的影响力传播
- A^3_{ij} > 0 表示用户 i 的信息可以在 3 步内传到用户 j
2. 推荐系统
- 如果用户 A 和商品 B 在 A^2 中有连接,可能意味着"用户 A 买了某商品,该商品被用户 C 也买了,而用户 C 买了商品 B"------形成间接推荐路径
3. 图同构检测
- 比较两个图的 A^k 是否相似,可作为图结构相似性的指标
4. PageRank 与随机游走
- 随机游走的概率转移矩阵本质上是归一化后的邻接矩阵,其幂次描述了长期访问概率
⚠️ 六、注意事项
| 问题 | 说明 |
|---|---|
| 路径 vs 简单路径 | A^k 统计的是 walk(可重复节点),不是 simple path |
| 计算复杂度 | 直接计算 A^k 复杂度高(O(n^3 \log k)),大图需稀疏矩阵优化 |
| 数值溢出 | 当 k 很大时,路径数量可能指数增长,导致数值爆炸 |
🧠 七、总结
| 操作 | 含义 |
|---|---|
| A | 长度为 1 的路径(直接连接) |
| A^2 | 长度为 2 的路径数量 |
| A^k | 长度为 k 的路径数量 |
| 所有长度 ≤ K 的路径总数(常用于图核、图相似性) |
邻接矩阵的幂,是图结构中"可达性"和"连接强度"的数学语言。
理解这一点,不仅能帮你掌握图论基础,还能为学习 GNN、知识图谱、复杂网络分析打下坚实基础。
📚 延伸阅读
- Godsil, C., & Royle, G. (2001). Algebraic Graph Theory
- Kipf, T. N., & Welling, M. (2017). Semi-Supervised Classification with Graph Convolutional Networks
- "Walks and paths in graphs" -- MIT OpenCourseWare
📌 欢迎关注我的博客,获取更多图机器学习与数学直观解释!