leetcode2826.将三个组排序

class Solution {
    public int minimumOperations(List<Integer> nums) {
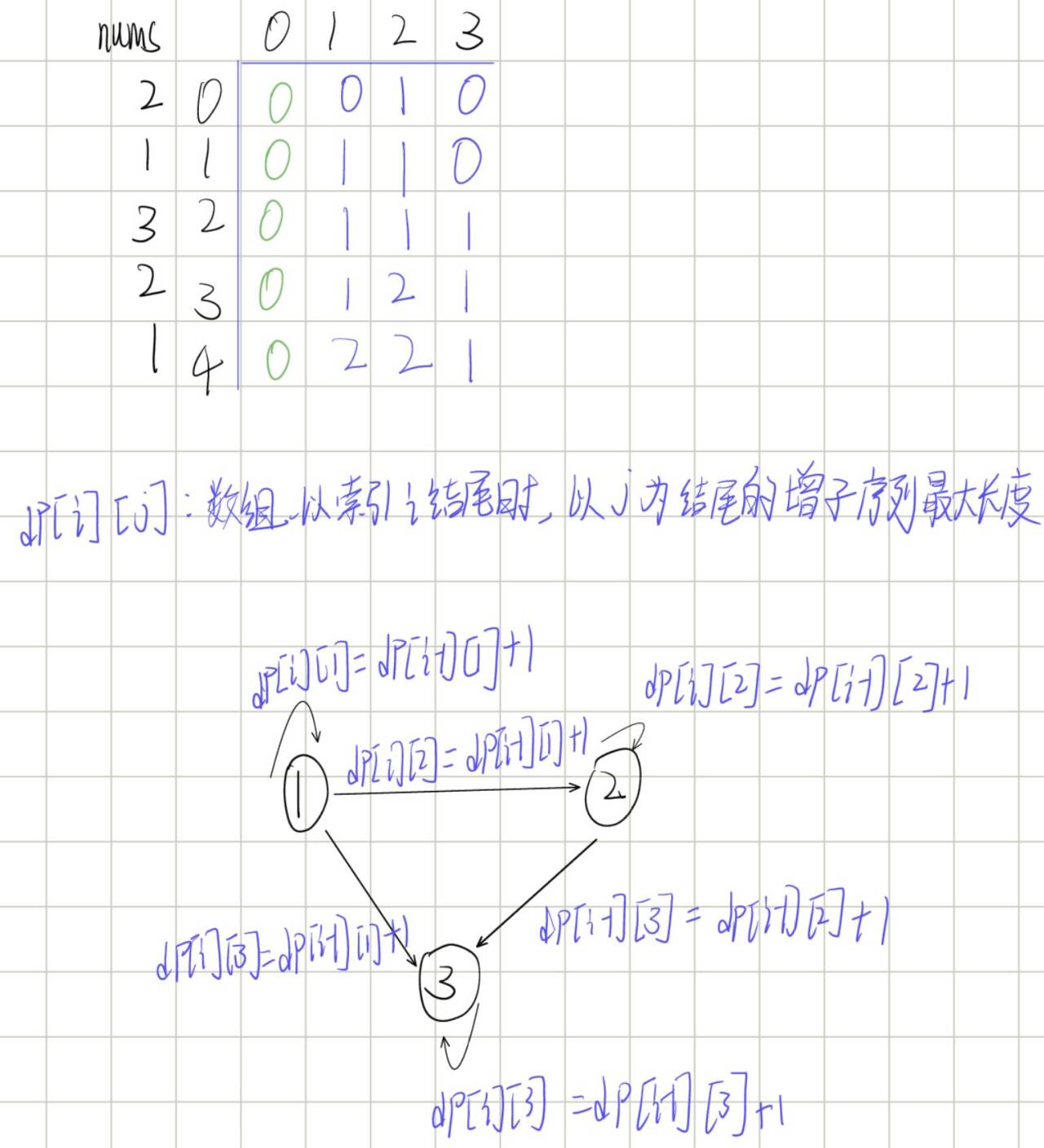
        int[][] dp = new int[nums.size()][3 + 1];
        dp[0][nums.get(0)]=1;
        for (int i = 1; i < nums.size(); i++) {
            dp[i][1]=dp[i-1][1];
            dp[i][2]=dp[i-1][2];
            dp[i][3]=dp[i-1][3];
            switch (nums.get(i)){
                case 1 -> dp[i][1] = Math.max(dp[i - 1][1] + 1, dp[i - 1][0] + 1);
                case 2 -> dp[i][2] = Math.max(dp[i - 1][2] + 1, dp[i - 1][1] + 1);
                case 3-> dp[i][3] = Math.max(dp[i - 1][3] + 1, Math.max(dp[i - 1][2] + 1, dp[i - 1][1] + 1));
            }
        }
        int n = nums.size();
        return n - Math.max(dp[n - 1][1], Math.max(dp[n - 1][2], dp[n - 1][3]));
    }
}

优化版本

class Solution {
    public int minimumOperations(List<Integer> nums) {
        //1.定义状态
        int _1 = 0, _2 = 0, _3 = 0;//分别表示以1、2、3结尾的子序列长度
        //2.状态转移
        for (int num : nums) {
            switch (num){
                case 1-> _1 = Math.max(_1 + 1, 1);
                case 2-> _2 = Math.max(_2 + 1, _1 + 1);
                case 3-> _3 = Math.max(_3 + 1, Math.max(_2 + 1, _1 + 1));
            }
        }
        //3.返回结果
        return nums.size() - Math.max(_1, Math.max(_2, _3));
    }
}