
Sage Husa自适应粒子滤波,用于克服初始Q和R不准确而带来的滤波误差较大的问题,使用一维非线性的状态和观测,方便学习和修改相似的模型。
文章目录
程序介绍
代码概述
本文介绍的代码是基于 MATLAB 的一维非线性系统自适应粒子滤波算法实现,包含了 Sage-Husa 自适应噪声估计和经典粒子滤波的对比。
- 实现了非线性状态方程 和非线性观测方程的粒子滤波
- 使用 Sage-Husa 自适应算法在线估计系统噪声 Q 和观测噪声 R
- 与经典粒子滤波进行性能对比
- 提供了完整的性能评估和可视化
算法特点
系统模型
- 状态方程 :
X(k) = X(k-1)^0.5 + X(k-1) + w(k)(非线性) - 观测方程 :
Z(k) = X(k)^0.5 + v(k)(非线性) - 系统噪声:
w(k) ~ N(0, Q_true) - 观测噪声:
v(k) ~ N(0, R_true)
自适应机制
matlab
% Sage-Husa 自适应估计
R_new = max(V_measured - V_predicted, 0.01); % 防止负值
R = b * R + (1 - b) * R_new; % 指数平滑更新
Q_new = max(var(x_err), 0.01);
Q = b * Q + (1 - b) * Q_new;代码结构
- 参数初始化 (采样率、粒子数、噪声参数等)
- 数据生成 (真实状态和观测值)
- 经典粒子滤波 (固定噪声参数)
- 自适应粒子滤波 (在线估计 Q, R)
- 结果可视化 (状态估计、误差、噪声估计)
- 性能评估 (RMSE, MAE, 最大值, 标准差)
输出结果
- 状态估计对比图
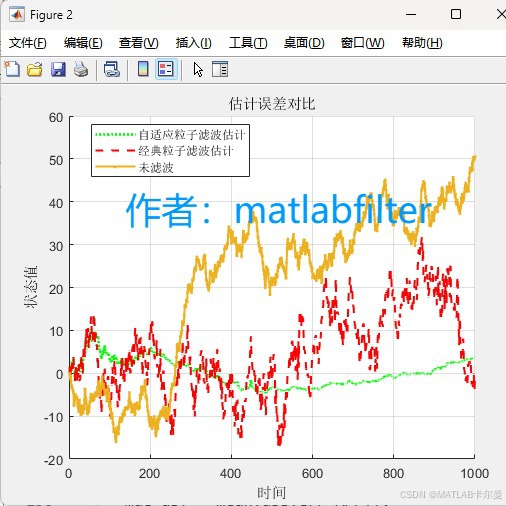
- 估计误差对比图
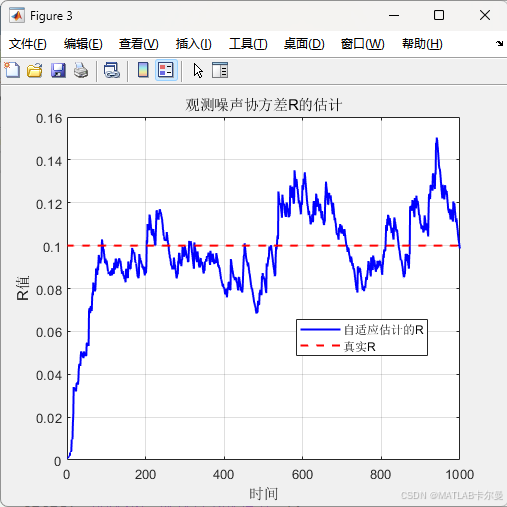
- 观测噪声 R 的估计过程图
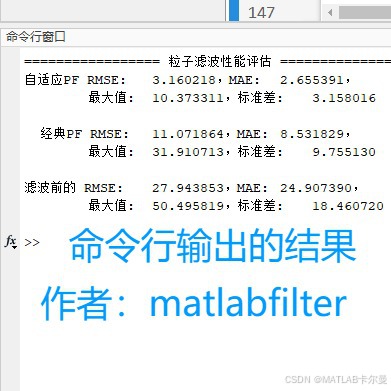
- 详细的性能指标表格
运行结果
状态曲线:
状态误差曲线:
观测噪声协方差矩阵R的估计曲线:
命令行截图:
MATLAB源代码
部分代码如下:
matlab
% 一维非线性状态、非线性观测的Sage Husa自适应PF(粒子滤波)例程
% 作者:matlabfilter
% 2025-09-28/Ver1
clear; %清空工作区变量
clc; %清空命令行内容
close all; %关闭所有窗口(主窗口除外)
rng(0); % 设置固定的随机数种子
%% 初始化参数
T = 1; % 采样率
t = T:T:1000; % 时间序列
N = 1000; % 粒子数量
Q_true = 1; % 真实系统噪声协方差
R_true = 0.1; % 真实观测噪声协方差
Q = 0.5; % 初始系统噪声协方差估计值
R = 0.001; % 初始观测噪声协方差估计值
b = 0.98; % 遗忘因子
d = 1 - b; % 辅助参数
X = zeros(1, length(t)); % 真实状态
X_ = zeros(1, length(t)); % 未滤波状态状态
Z = zeros(1, length(t)); % 观测值
X(1) = 3; % 状态初值
X_(1) = 3; % 状态初值
Z(1) = sqrt(X(1)) + sqrt(R_true) * randn; % 初始观测值
particles = X(1) + sqrt(Q) * randn(N, 1); % 初始化粒子
% 存储结果
% 系统噪声和观测噪声
%% 生成真实状态和观测值
figure;
plot(t, R_num, 'b-', 'LineWidth', 1.5);
hold on;
plot(t, ones(size(t)) * R_true, 'r--', 'LineWidth', 1.5);
title('观测噪声协方差R的估计');
legend('自适应估计的R', '真实R', 'Location', 'best');
xlabel('时间');
ylabel('R值');
grid on;
%% 性能评估
fprintf('================= 粒子滤波性能评估 =================\n');
% 计算误差
rmse_apf = sqrt(mean(err_APF.^2));
rmse_pf = sqrt(mean(err_PF.^2));
rmse_ = sqrt(mean(err_X_.^2));
mae_apf = mean(abs(err_APF));
mae_pf = mean(abs(err_PF));
mae_ = mean(abs(err_X_));
% 计算最大值和标准差
max_apf = max(abs(err_APF));
max_pf = max(abs(err_PF));
max_ = max(abs(err_X_));
std_apf = std(err_APF);
std_pf = std(err_PF);
std_ = std(err_X_);
% 输出结果
fprintf('自适应PF RMSE:\t%.6f,MAE:\t%.6f,\n\t\t最大值:\t%.6f,标准差:\t%.6f\n\n', rmse_apf, mae_apf, max_apf, std_apf);
fprintf(' 经典PF RMSE:\t%.6f,MAE:\t%.6f,\n\t\t最大值:\t%.6f,标准差:\t%.6f\n\n', rmse_pf, mae_pf, max_pf, std_pf);
fprintf('滤波前的 RMSE:\t%.6f,MAE:\t%.6f,\n\t\t最大值:\t%.6f,标准差:\t%.6f\n\n', rmse_, mae_, max_, std_);更多代码可在专栏文章查看:
https://blog.csdn.net/callmeup/article/details/153532639?spm=1011.2415.3001.5331
或通过下方链接单独下载:
https://download.csdn.net/download/callmeup/92163513
如需帮助,或有导航、定位滤波相关的代码定制需求,请点击下方卡片联系作者