力扣面试经典150题打卡

题目链接:55. 跳跃游戏 - 力扣（LeetCode）

大致思路

举例:nums=3,2,1,0,4

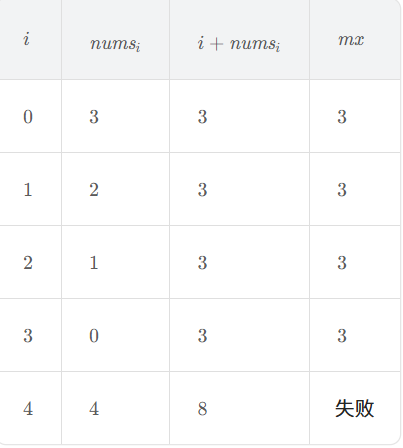
看图理解代码的意思,当i的值小于mx的值的时候,这个地方就到不了

1从左到右遍历数组nums,同时查看可以跳的最远距离,初始值设置为0(最远距离),

2:遍历过程中,如果i>maxNum,说明没有办法跳到i这个地方,就直接返回false,既然i的这个位置都到不了了,所以最后的位置也到达不了

3如果没有,就将maxNum的值进行更新,更新为maxNum和i+numsi之间的最大值即可

4没有返回false就是true了

代码体现:

class Solution {
    public boolean canJump(int[] nums) {
        int maxNum =0;
        for(int i=0;i<nums.length;i++){
            if(i>maxNum){
                return false;
            }
            maxNum = Math.max(maxNum,i+nums[i]);
        }
        return true;
    }
}

题目链接:45. 跳跃游戏 II - 力扣（LeetCode）

思路一:

第二道题看的是力扣官方的题解

1逆向思维,首先找到可以跳到最后一个位置,而且距离最后一个位置最远的地方,

2将这个最远的地方的i赋值给position,步数(step++)

3紧接着找现在i=position位置,前面可以跳到的,而且距离最远的一个地方,在进行步骤二的操作

误区:

这里可能会有人有误区,i++,i一直在变大,怎么退出循环呢,请注意break,它结束的是内层循环,break一次后,内层循环仍然要从0开始循环,所以,只有当position逆向到达起点的时候,循环结束,得到结果.

下面给出一个举例说明:

举例说明（数组 [2,3,1,1,4]）

• 初始 position = 4（终点），step = 0。
• 内层循环找 i：
  • i=0：2+0=2 < 4 → 不满足。
  • i=1：3+1=4 ≥ 4 → 满足，更新 position = 1，step = 1。
• 再次进入 while 循环（position=1 > 0）：
  • 内层循环找 i：
    • i=0：2+0=2 ≥ 1 → 满足，更新 position = 0，step = 2。
• position=0，循环结束，返回 step=2（与最优解一致）。

代码体现:

class Solution {
    public int jump(int[] nums) {
        int position =nums.length-1;
        int step=0;
        while(position>0){
            for(int i=0;i<position;i++){
                if(nums[i]+i>=position){
                    position=i;
                    step++;
                    break;
                }
            }
        }
        return step;
    }
}

思路二:

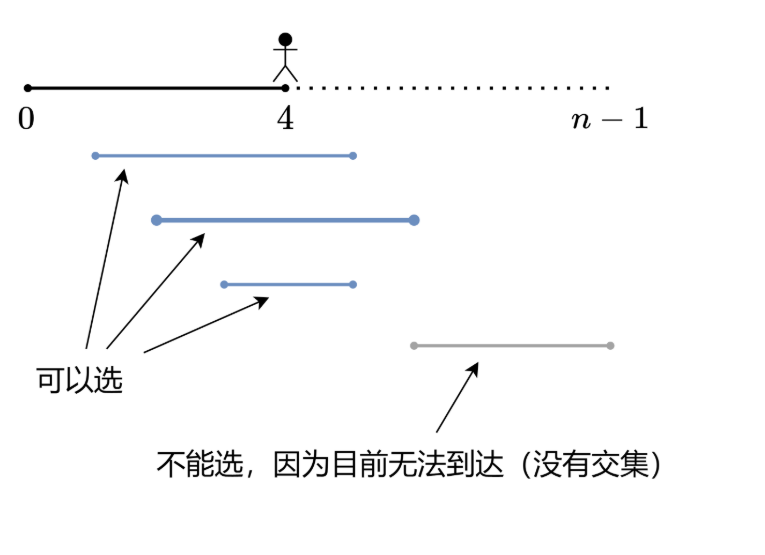
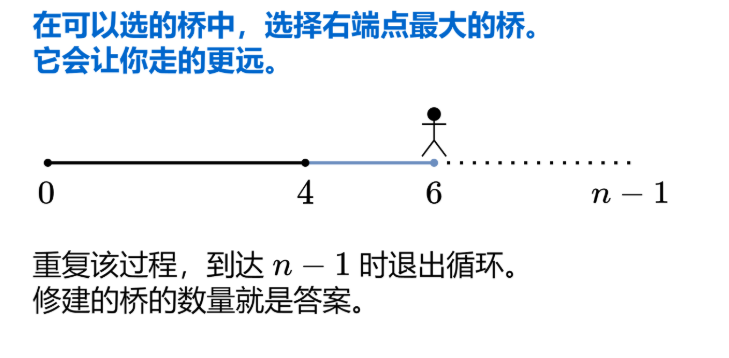
1正向思维,这里借助灵神的建桥思想,通过循环数组,获取可以建造的最大长度的桥段

2循环进行,当循环到i==目前建造桥段的最右端的时候,这时候必须要建造新桥

3新桥的长度已经获取,取得是nextLength和i+numsi的较大值,新桥的长度确定了,那么目前建造桥段的最右端距离也确定了,赋值给curRight(已经建造桥段的最右端距离)

4当必须建桥的时候,计数器也要做一次++操作,最后返回计数器即可

题目的隐含意思:数组一定可以到达最后一个位置,所以我们的循环添加为len-1,是因为curRight后边肯定会大大覆盖最后一个位置,下面是灵神的问答

代码如下:

class Solution {
    public int jump(int[] nums) {
        int len = nums.length;
        int curRight= 0;
        int nextLength=0;
        int ans=0;

        for(int i=0;i<len-1;i++){
            nextLength = Math.max(nextLength,i+nums[i]);
            if(i==curRight){
                curRight = nextLength;
                ans++;
            }
        }
        return ans;
    }
}