问题描述:
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k的子数组的个数。
子数组是数组中元素的连续非空序列。
示例1:
**输入:**nums = [1,1,1], k = 2
**输出:**2
**解释:**和为 2 的子数组有 [1,1] (索引 0-1) 和 [1,1] (索引 1-2)
示例2:
输入: nums = [1,2,3], k = 3
输出: 2
**解释:**和为 3 的子数组有 [1,2] (索引 0-1) 和 [3] (索引 2-2)
解决方法:
方法一:暴力枚举
思路:枚举所有的子数组,计算它们的和,统计等于k的个数。
python
def subarraySum_brute_force(nums, k):
count = 0
n = len(nums)
# 枚举所有子数组的起始位置
for start in range(n):
current_sum = 0
# 枚举所有子数组的结束位置
for end in range(start, n):
# 计算子数组 nums[start..end] 的和
current_sum += nums[end]
# 如果和等于 k,计数加 1
if current_sum == k:
count += 1
return count复杂度分析:
- 时间复杂度:O(n²) 双层循环枚举所有子数组
- 空间复杂度:O(1) 只使用了常数空间
评价:数据量小时可以使用,对于数据规模过大时不高效。
方法二:前缀和+哈希表
思路:利用前缀和技巧(sum[ i : j ] = sum[ j ] - sum[ i - 1 ]),通过哈希表记录之前出现过的前缀和及其次数,从而在 O(1) 时间内判断是否存在满足条件的子数组。
python
class Solution:
def subarraySum(self, nums: List[int], k: int) -> int:
from collections import defaultdict
#创建前缀和计数字典 记录每个前缀和出现的次数 sum[i:j] = sum[j] - sum[i-1]
prefix_count = defaultdict(int)
#初始化
prefix_count[0] = 1
current_sum = 0
count = 0
#遍历数组元素
for num in nums:
#更新当前前缀和
current_sum += num
#检查是否存在某个前缀和等于 current_sum - k
#若存在 从那个位置到当前位置子数组和为k
if current_sum - k in prefix_count:
#更新计数 增加的数量等于该前缀和出现的次数
count += prefix_count[current_sum - k]
#将当前前缀和计数加1 记录到字典
prefix_count[current_sum] += 1
return count 复杂度分析:
- 时间复杂度:O(n) 只需遍历数组一次
- 空间复杂度:O(n) 最坏情况下需要存储 n 个不同的前缀和
评价:最优解。
问题详解:
1、前缀和+哈希表算法步骤:
-
使用哈希表记录每个前缀和出现的次数;
-
初始化前缀和为 0 出现 1 次(对应空数组);
-
遍历数组,累计当前前缀和;
-
检查 current_sum - k 是否在哈希表中;
-
更新哈希表中当前前缀和的计数。
2、为什么初始化 prefix_count [0] = 1:
当数组的第一个元素就是所找的k时,此时 current_sum - k = 0;若没有初始化 prefix_count [0] = 1,就会错过这个子数组。
3、为什么 count += prefix_count[current_sum - k]而不是count += 1:
因为同一前缀和的结果可能出现多次,每次所对应的位置不同。
例如 nums = [4,1,2,3,0,6,2,4] k = 6。
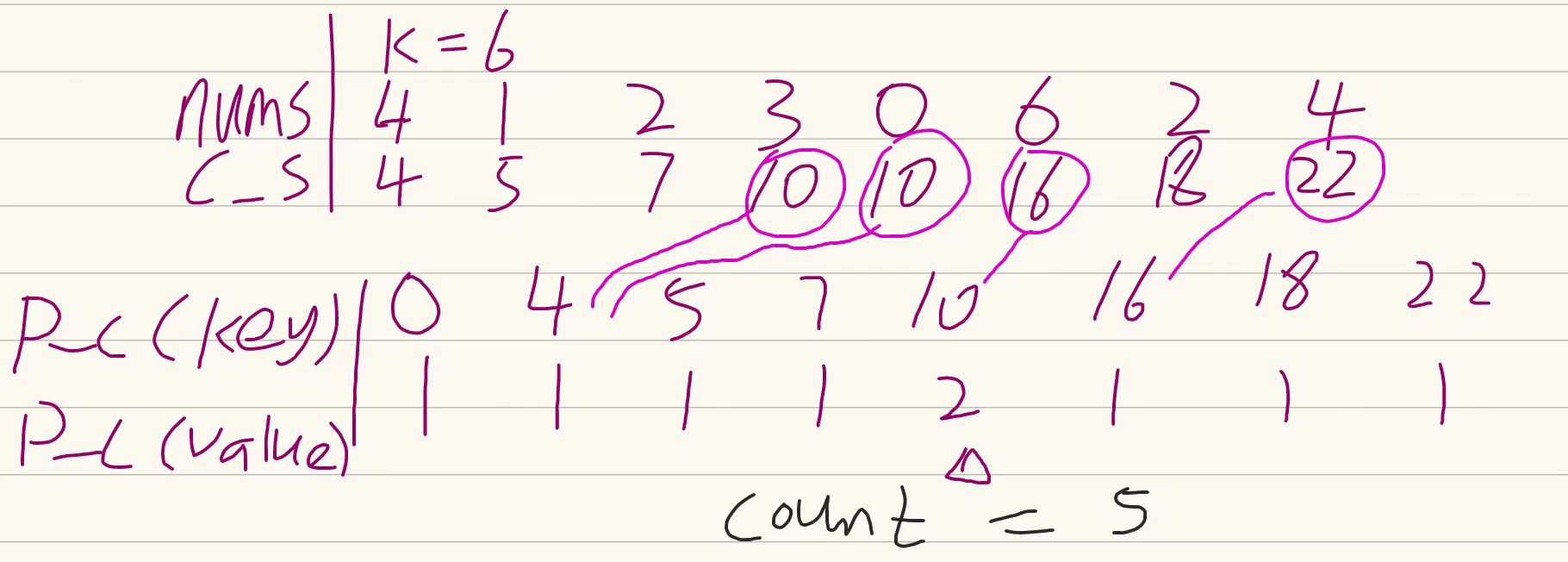
总结:
| 方法 | 时间复杂度 | 空间复杂度 | 优点 | 缺点 |
| 暴力枚举 | O(n²) | O(1) | 实现简单 | 数据量大时效率低 |
| 前缀和+哈希表 | O(n) | O(n) | 最优解,效率高 | 需要额外空间 |
|---|
-
前缀和技巧可以将子数组和问题转化为两数之差问题;
-
初始化 prefix_count [0] = 1 是处理边界情况的关键。