题目
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
数据范围
k == lists.length
0 <= k <= 104
0 <= lists[i].length <= 500
-104<= lists[i][j] <= 104
lists[i] 按 升序 排列
lists[i].length 的总和不超过 104
测试用例
示例1
java
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6示例2
java
输入:lists = []
输出:[]示例3
java
输入:lists = [[]]
输出:[]题解1(博主思路,把这些链表链接起来,然后用上一套题的方法排序,时间nlogn,空间o1)
java
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
int length = lists.length;
// 边界检查:如果是空数组,或者只有一个空链表,直接返回 null
if (length == 0 || (lists[0] == null && length == 1)) {
return null;
}
ListNode head = null;
boolean flag = true; // 用于标记是否找到了第一个非空的链表头
// --- 阶段一:暴力拼接 ---
// 遍历整个链表数组,将所有非空链表首尾相连
for (int i = 0; i < length; i++) {
if (lists[i] != null) {
// 如果是第一个遇到的非空链表,记录它为最终大链表的头节点
if (flag) {
head = lists[i];
flag = false;
}
// 找到当前链表 lists[i] 的尾节点 (tail)
ListNode tnode = lists[i];
while (tnode.next != null) {
tnode = tnode.next;
}
// 寻找数组中下一个非空的链表
int pos = i + 1;
while (pos < length && lists[pos] == null)
pos = pos + 1;
// 如果找到了下一个非空链表,将当前尾节点指向它
// 实现:List_A_Tail -> List_B_Head
if (pos < length) {
tnode.next = lists[pos];
// 更新索引 i,跳过中间那些 null,直接跳到刚刚接上的那个链表的前一个位置
// (循环体会执行 i++,所以这里设为 pos-1)
i = pos - 1;
}
} else {
continue;
}
}
// --- 阶段二:全局排序 ---
// 将拼接好的巨型链表扔进去进行排序
ListNode res = sortList(head);
return res;
}
// 这是一个标准的【链表归并排序】实现(迭代版/自底向上)
// 时间复杂度 O(N log N),空间复杂度 O(1)
public static ListNode sortList(ListNode head) {
if (head == null) {
return head;
}
// 1. 计算链表总长度
int length = 0;
ListNode tnode = head;
while (tnode != null) {
length++;
tnode = tnode.next;
}
// 引入哑节点,方便操作头部的变化
ListNode dummyHead = new ListNode(0, head);
// 2. 自底向上归并
// tlen 是子链表的长度,从 1 开始,每次翻倍:1 -> 2 -> 4 -> 8 ...
for (int tlen = 1; tlen < length; tlen *= 2) {
ListNode cur = dummyHead.next; // cur 用来遍历链表
ListNode pre = dummyHead题解2(顺序合并,时间k²n,空间O1)
java
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
ListNode ans = null;
for (int i = 0; i < lists.length; ++i) {
ans = mergeTwoLists(ans, lists[i]);
}
return ans;
}
public ListNode mergeTwoLists(ListNode a, ListNode b) {
if (a == null || b == null) {
return a != null ? a : b;
}
ListNode head = new ListNode(0);
ListNode tail = head, aPtr = a, bPtr = b;
while (aPtr != null && bPtr != null) {
if (aPtr.val < bPtr.val) {
tail.next = aPtr;
aPtr = aPtr.next;
} else {
tail.next = bPtr;
bPtr = bPtr.next;
}
tail = tail.next;
}
tail.next = (aPtr != null ? aPtr : bPtr);
return head.next;
}
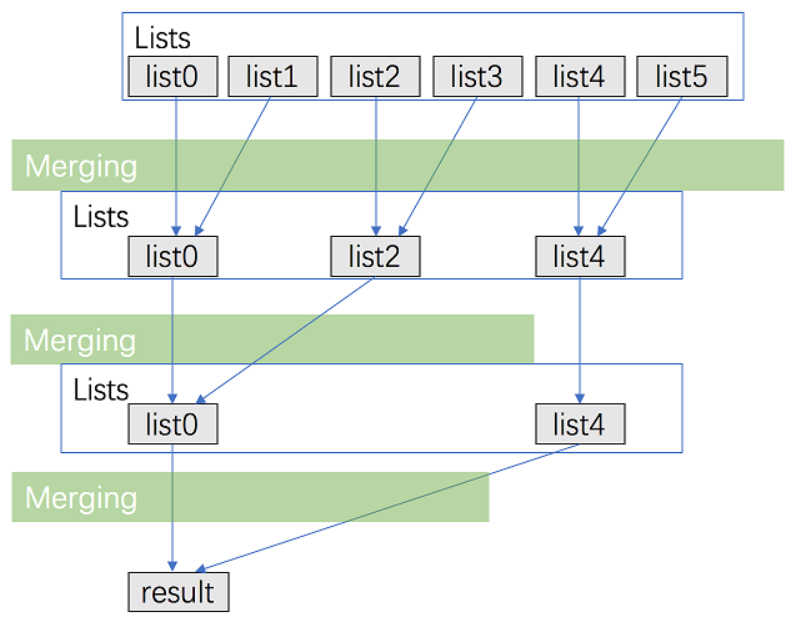
}题解3(分治合并,时间Oknlogk,空间Ologk)
java
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
// 主函数:入口
public ListNode mergeKLists(ListNode[] lists) {
// 调用分治合并函数,范围是从第一个链表(0)到最后一个链表(length - 1)
return merge(lists, 0, lists.length - 1);
}
/**
* 核心分治方法
* 作用:将 lists[l] 到 lists[r] 这一段的链表合并成一个有序链表
*/
public ListNode merge(ListNode[] lists, int l, int r) {
// 1. 递归基准条件(Base Case):
// 当左边界等于右边界时,说明只剩下一个链表了,直接返回它,不需要合并。
if (l == r) {
return lists[l];
}
// 边界处理:防止数组为空的情况 (l > r)
if (l > r) {
return null;
}
// 2. 「分」(Divide):
// 找出中间位置。 (l + r) >> 1 等同于 (l + r) / 2,位运算效率更高
int mid = (l + r) >> 1;
// 3. 「治」(Conquer):
// 递归调用:
// - merge(lists, l, mid): 负责合并左半部分,返回左边合并好的大链表
// - merge(lists, mid + 1, r): 负责合并右半部分,返回右边合并好的大链表
// 最后调用 mergeTwoLists 将左右两个大链表合并成最终结果
return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));
}
/**
* 双链表合并方法
* 作用:合并两个有序链表 a 和 b
*/
public ListNode mergeTwoLists(ListNode a, ListNode b) {
// 判空处理:如果其中一个为空,直接返回另一个
if (a == null || b == null) {
return a != null ? a : b;
}
// 创建哑节点(dummy head),作为结果链表的头部占位符
ListNode head = new ListNode(0);
// tail 用于指向当前结果链表的尾部
// aPtr 和 bPtr 作为游标,分别在 a 和 b 链表上移动
ListNode tail = head, aPtr = a, bPtr = b;
// 当两个链表都还有节点时,进行比较
while (aPtr != null && bPtr != null) {
// 谁小选谁,并将对应的指针后移
if (aPtr.val < bPtr.val) {
tail.next = aPtr;
aPtr = aPtr.next;
} else {
tail.next = bPtr;
bPtr = bPtr.next;
}
// 尾指针永远指向最新的节点
tail = tail.next;
}
// 收尾工作:
// 循环结束后,肯定有一个链表先走完。
// 将 tail 直接指向剩下的那个链表(因为剩下的肯定是有序的,直接接上即可)
tail.next = (aPtr != null ? aPtr : bPtr);
// 返回哑节点的下一个节点,即真正的头节点
return head.next;
}
}题解4(优先队列,时间Oknlogk,空间Ok)
java
class Solution {
// 定义一个包装类 Status,用于放入优先队列中
// 实现了 Comparable 接口,以便优先队列能自动根据 val 值进行排序
class Status implements Comparable<Status> {
int val;
ListNode ptr;
Status(int val, ListNode ptr) {
this.val = val;
this.ptr = ptr;
}
// 定义比较规则:从小到大排序(最小堆)
public int compareTo(Status status2) {
return this.val - status2.val;
}
}
// 创建一个小顶堆(PriorityQueue),队列头部永远是 val 最小的节点
PriorityQueue<Status> queue = new PriorityQueue<Status>();
public ListNode mergeKLists(ListNode[] lists) {
// 1. 初始化阶段:
// 遍历所有链表的头节点。只要链表非空,就把它放入队列。
// 这样队列里就包含了所有链表当前的"领头羊"。
for (ListNode node: lists) {
if (node != null) {
queue.offer(new Status(node.val, node));
}
}
// 创建一个哑节点(dummy head),用于方便地构建结果链表
ListNode head = new ListNode(0);
ListNode tail = head;
// 2. 循环合并阶段:
// 只要队列不为空,就说明还有节点没处理完
while (!queue.isEmpty()) {
// A. 从队列中取出当前最小的节点 f (poll操作)
Status f = queue.poll();
// B. 将这个最小节点接到结果链表的末尾
tail.next = f.ptr;
tail = tail.next;
// C. 关键步骤(补充弹药):
// 如果刚刚取出的那个节点所在的链表后面还有节点,
// 就把那个链表的"下一个节点"入队。
// 这样能保证队列里始终维护着 k 个链表当前的头部候选人。
if (f.ptr.next != null) {
queue.offer(new Status(f.ptr.next.val, f.ptr.next));
}
}
// 返回哑节点的下一个节点,即真正的结果链表头
return head.next;
}
}思路
这道题虽然整体看起来代码量大,其实思路不难,如果100题的链表是一道一道写过来的,这道题都能较为轻松的解决,唯一需要住的是,链表中可能存在空链表,用有些方法的时候,需要对其进行一个判定。
因为博主刚做了排序,就直接干脆用排序做了,当然时间复杂度肯定是不优的,但空间复杂度能做到O1。当然大家还是看其他几个方法比较好,写起来更方便,效果还更优。
追求时间复杂度的话使用优先队列与分治法,这两者都不难,能想起来有这个方法就是成功。
追求空间复杂度就顺序合并,我连备注都不想加,太简单了。