Leetcode 279. 完全平方数

Greedy Alg2025-10-30 12:59

题目描述

给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例

示例 1：

复制代码

输入：n = 12
输出：3 
解释：12 = 4 + 4 + 4

示例 2：

复制代码

输入：n = 13
输出：2
解释：13 = 4 + 9

解法

动态规划

解题思路

可以依据题目的要求写出状态表达式：f $i$ 表示最少需要多少个数的平方来表示整数 i。

这些数必然落在区间 $1, sqrt(i)$ 。我们可以枚举这些数，假设当前枚举到 j，那么我们还需要取若干数的平方，构成 i−j*j。此时我们发现该子问题和原问题类似，只是规模变小了。这符合了动态规划的要求，于是我们可以写出状态转移方程。

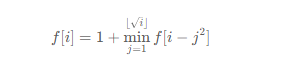
其中 f $0$ =0 为边界条件，实际上我们无法表示数字 0，只是为了保证状态转移过程中遇到 j 恰为 sqrt(i)的情况合法。

同时因为计算 f $i$ 时所需要用到的状态仅有 f $i−j\*j$ ，必然小于 i，因此我们只需要从小到大地枚举 i 来计算 f $i$ 即可。

cpp 复制代码

class Solution {
public:
    int numSquares(int n) {
        vector<int> f(n + 1);
        for(int i = 1;i <= n;i ++){
            int minn = INT_MAX;
            for(int j = 1;j * j <= i;j ++){
                minn = min(minn,f[i - j * j]);
            }
            f[i] = minn + 1;
        }
        return f[n];

    }
};

时间复杂度O（N^2），空间复杂度O（N）