算法刷题--螺旋矩阵II+区间和+开发商购买土地

文章目录

• • [1、59 螺旋矩阵II](#1、59 螺旋矩阵II)
  • • [1. 观察切入点：螺旋的本质是什么？](#1. 观察切入点：螺旋的本质是什么？)
    • [2. 核心原理：四边边界法](#2. 核心原理：四边边界法)
    • [3. 思路推演：逻辑四部曲](#3. 思路推演：逻辑四部曲)
    • [5. 避坑指南](#5. 避坑指南)
    • 总结：这种解法的精髓
    • 第一部分：告知总行数
    • 第二部分：创建"列数清单"
    • 第三部分：创建矩阵主体
    • • [1. 分配"行指针"数组](#1. 分配“行指针”数组)
      • [2. 循环分配每一行的空间](#2. 循环分配每一行的空间)
    • 总结：内存全景图
    • [为什么不能直接定义 `int arr[n][n]`？](#为什么不能直接定义 int arr[n][n]？)
  • [2、54 螺旋矩阵](#2、54 螺旋矩阵)
  • [3、48 旋转图像](#3、48 旋转图像)
  • • [1. 核心观察：旋转 90 度的坐标规律](#1. 核心观察：旋转 90 度的坐标规律)
    • [2. 思路一：几何分解法（最推荐，最直观）](#2. 思路一：几何分解法（最推荐，最直观）)
    • • 第一步：主对角线翻转 (Transpose)
      • 第二步：左右镜像翻转 (Mirror Flip)
    • [3. 思路二：分层环状替换](#3. 思路二：分层环状替换)
    • [4. 避坑指南](#4. 避坑指南)
    • 总结
    • [1. 核心逻辑：四角循环倒手](#1. 核心逻辑：四角循环倒手)
    • • 坐标对应关系推导
    • [2. 代码逐行详解](#2. 代码逐行详解)
    • [3. 两种解法对比：哪个更好？](#3. 两种解法对比：哪个更好？)
    • • 总结建议：
  • [4、58 区间和](#4、58 区间和)
  • • [1. 语法层面的拆解](#1. 语法层面的拆解)
    • [2. 逻辑层面的含义：只要有输入，就一直跑](#2. 逻辑层面的含义：只要有输入，就一直跑)
    • [3. 为什么在"前缀和"题目中这么写？](#3. 为什么在“前缀和”题目中这么写？)
    • [4. 避坑小贴士](#4. 避坑小贴士)
    • 总结
  • [5、44 开发商购买土地](#5、44 开发商购买土地)

1、59 螺旋矩阵II

题目

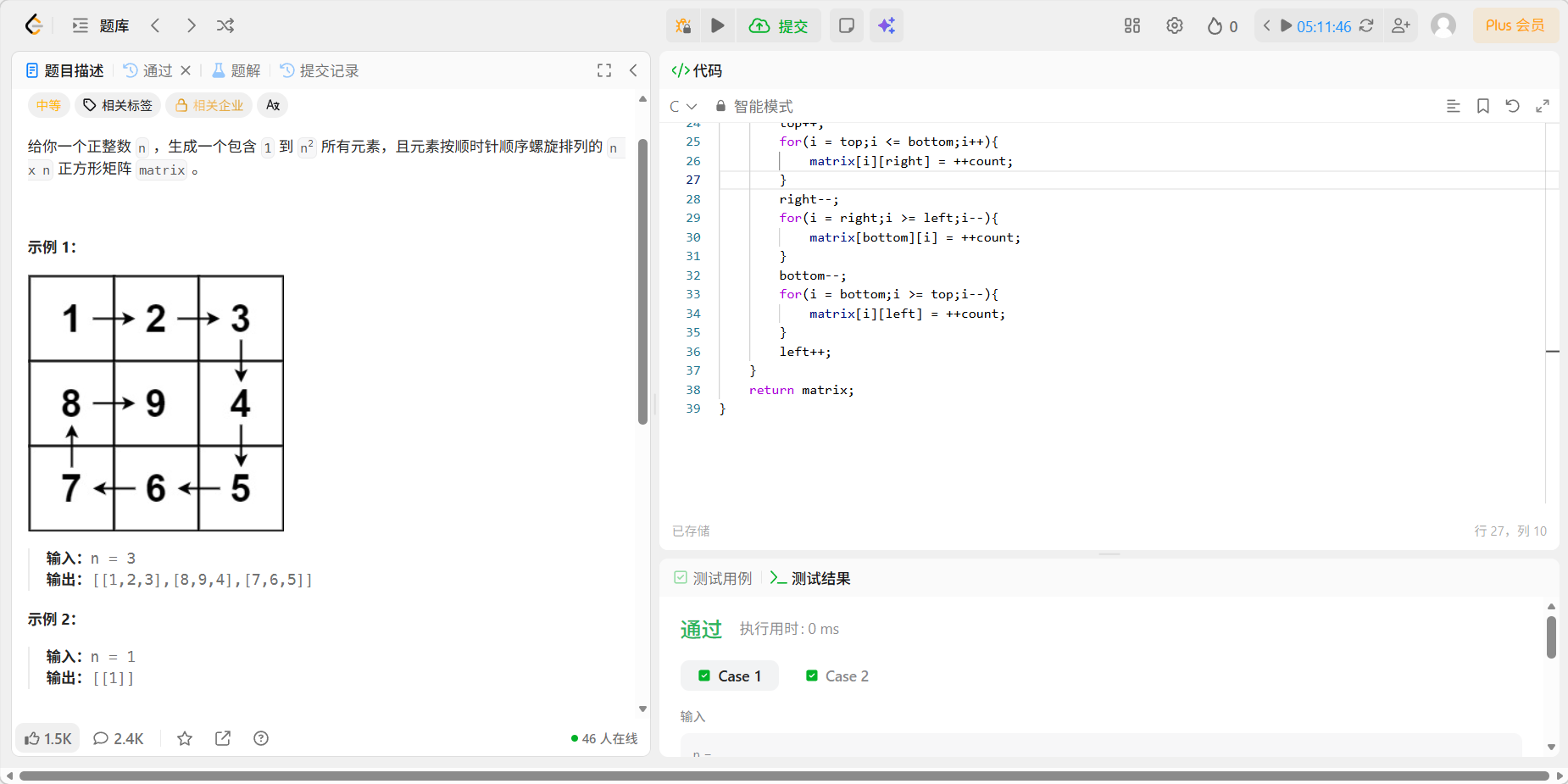
"螺旋矩阵 II" (Spiral Matrix II) 是一道非常经典的模拟题 。它不涉及复杂的数据结构或高级算法，考察的是你对边界控制的细心程度和逻辑严密性。

1. 观察切入点：螺旋的本质是什么？

螺旋矩阵的生成过程就像是在一个正方形广场上"绕圈圈"。

• 方向规律 ：总是按照 从左到右 从上到下 从右到左 从下到上 的顺序循环。
• 边界递减：每当我们填满一行或一列，这一行或一列就"失效"了，剩下的可活动范围（边界）就会缩小。

---

2. 核心原理：四边边界法

我们可以定义四个变量来代表当前的"活动墙壁"：

• top：当前未填充的最上行
• bottom：当前未填充的最下行
• left：当前未填充的最左列
• right：当前未填充的最右列

---

3. 思路推演：逻辑四部曲

我们要填入 1 1 1 到 n 2 n^2 n2 的数字，每填满一边，就收缩对应的边界：

1. 从左到右 ：在 top 行，从 left 列填到 right 列。

• 填完后，第一行就满了，top++（最上边界下移）。

2. 从上到下 ：在 right 列，从 top 行填到 bottom 行。

• 填完后，最右列就满了，right--（最右边界左移）。

3. 从右到左 ：在 bottom 行，从 right 列填到 left 列。

• 填完后，最下行就满了，bottom--（最下边界上移）。

4. 从下到上 ：在 left 列，从 bottom 行填到 top 行。

• 填完后，最左列就满了，left++（最左边界右移）。

重复以上四个步骤，直到填满 n 2 n^2 n2 个数字为止。

---

5. 避坑指南

• 边界相等判断 ：在 for 循环中，一定要用 i <= right 或 i >= left，因为边界上的那个点也是需要填写的。
• 循环结束条件 ：最稳妥的办法是使用 num <= n * n。
• 内存分配 ：在 C 语言中，returnColumnSizes 必须分配一个长度为 n 的数组，且每个元素都赋值为 n。

总结：这种解法的精髓

这种"四边界收缩法"的精髓在于自动处理边界更新。你不需要去纠结每一圈的长度是多少，只需要机械地执行"填一边，缩一格"，逻辑非常清晰，不容易写出死循环或越界。

代码

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
int** generateMatrix(int n, int* returnSize, int** returnColumnSizes) {
    *returnSize = n;
    *returnColumnSizes = (int*)malloc(sizeof(int) * n);
    int** matrix = (int**)malloc(sizeof(int*)*n);
    for(int i = 0;i < n;i++){
        matrix[i] = (int*)malloc(sizeof(int) * n);
        (*returnColumnSizes)[i] = n;
    }
    int count = 0;
    int top = 0;
    int bottom = n-1;
    int left = 0;
    int right = n-1;
    int i = 0;
    while(count < n*n){
        for(i = left;i <= right;i++){
            matrix[top][i] = ++count;
        }
        top++;
        for(i = top;i <= bottom;i++){
            matrix[i][right] = ++count;
        }
        right--;
        for(i = right;i >= left;i--){
            matrix[bottom][i] = ++count;
        }
        bottom--;
        for(i = bottom;i >= top;i--){
            matrix[i][left] = ++count;
        }
        left++;
    }
    return matrix;
}

时间复杂度：O( n 2 n^2 n2)

空间复杂度：O( n 2 n^2 n2)

详细解释这段代码的每一行

returnSize = n;
returnColumnSizes = (int )malloc(sizeof(int) * n);

int** matrix = (int**)malloc(sizeof(int*)n);
for(int i = 0;i < n;i++){
matrix[i] = (int )malloc(sizeof(int) * n);

(*returnColumnSizes)[i] = n;

}

这段代码是 C 语言在处理动态二维数组 时的"标准模版"。在 LeetCode 中，系统需要知道你返回的矩阵有多少行 、每行有多少列 ，以及矩阵的具体内容。

我们把这段代码拆解为三个部分：行数说明 、列数说明表 、矩阵主体分配。

---

第一部分：告知总行数

*returnSize = n;

• 含义 ：returnSize 是一个传址参数（指针）。这行代码的意思是：把外部变量的值改写为 n 。
• 目的：告诉调用者："我为你准备的这个矩阵一共有 n 行。"

---

第二部分：创建"列数清单"

为了知道每一行有多少列，LeetCode 要求你返回一个数组，记录每一行的长度。

*returnColumnSizes = (int*)malloc(sizeof(int) * n);

• 含义：申请一个能存放 n 个整数的内存空间。
• 注意 ：returnColumnSizes 是一个二级指针（int**）。这行代码是让原本悬空的指针指向一块真实的数组空间。
• 目的：准备一个"记事本"，用来登记每一行的宽度。

---

第三部分：创建矩阵主体

这是最核心的内存分配，分两步走。

1. 分配"行指针"数组

int** matrix = (int**)malloc(sizeof(int*) * n);

• 含义 ：申请 n个空间，每个空间存的是一个指针 （int*）。
• 比喻：这就像是买了 n 个挂钩。每一个挂钩将来都要挂住一整行的数据。

2. 循环分配每一行的空间

for (int i = 0; i < n; i++) {
    matrix[i] = (int*)malloc(sizeof(int) * n); // 为第 i 行分配 n 个整数空间
    (*returnColumnSizes)[i] = n;              // 在"清单"里记录第 i 行有 n 列
}

• matrix[i] = ...：在每个挂钩上，挂上一串能存 n 个整数的盒子。
• (*returnColumnSizes)[i] = n：这是关键！它在刚才准备好的"记事本"上写下：第 i 行有 n 个元素。
• 注：加括号是因为 [] 优先级比 * 高，必须先解引用找到记事本，再写下标。

---

总结：内存全景图

如果你调用 generateMatrix(3, ...)，内存中会呈现出这样的布局：

变量名	存储的内容	指向哪里
*returnSize	3	告知行数为 3
*returnColumnSizes	[3, 3, 3]	告知每一行都是 3 列
matrix	[ptr0, ptr1, ptr2]	存放 3 个行指针
matrix[0]	[?, ?, ?]	存放第一行的 3 个数字

---

为什么不能直接定义 int arr[n][n]？

1. 栈 vs 堆 ：int arr[n][n] 是局部变量，存在栈上，函数结束内存就销毁了，外部程序会读到乱码。
2. 动态性 ：使用 malloc 是在堆 上申请内存，函数结束后内存依然存在，直到手动 free。

**理解了这段代码，你就掌握了 C 语言操作内存的灵魂。

2、54 螺旋矩阵

题目

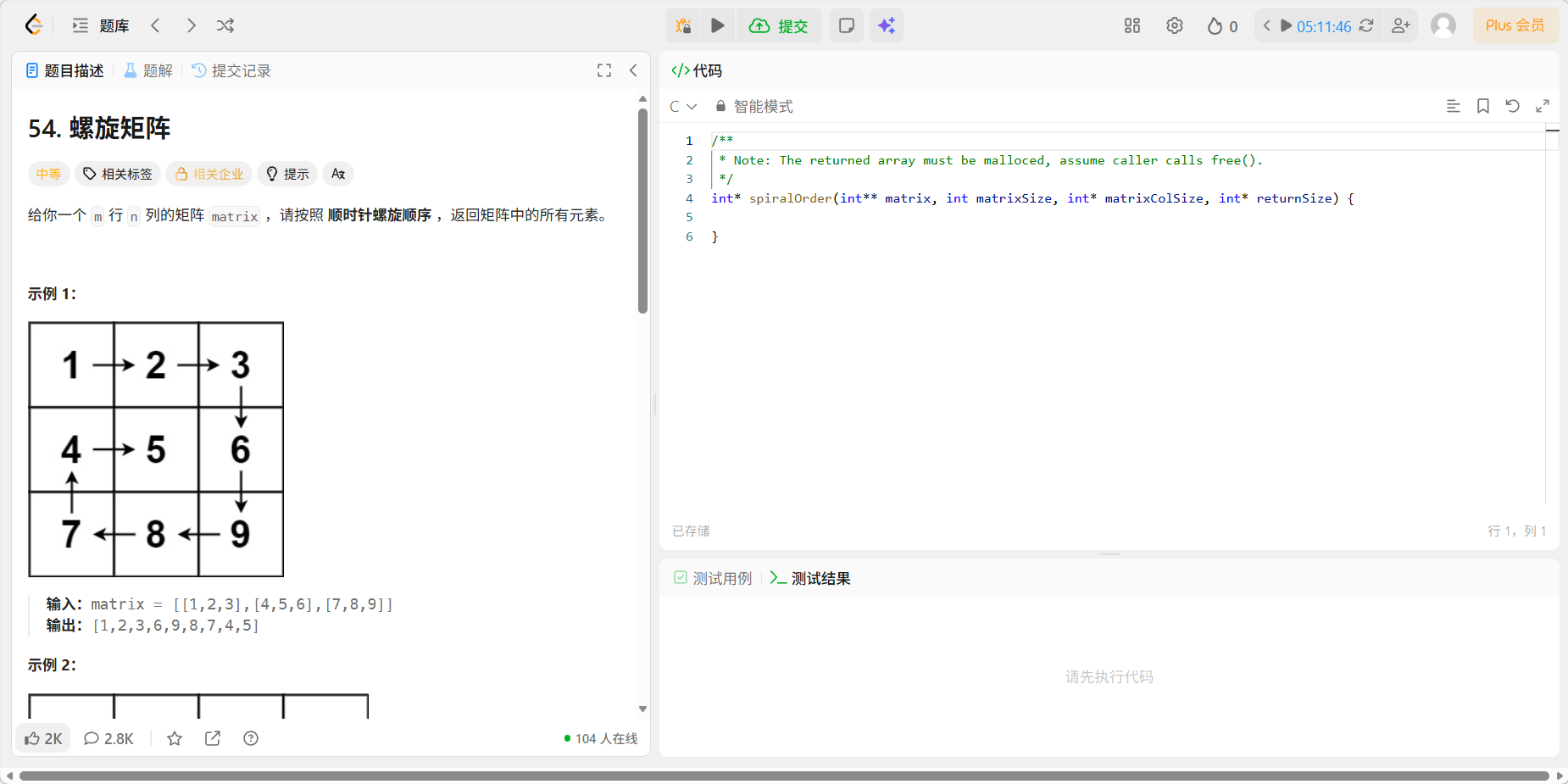
代码

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* spiralOrder(int** matrix, int matrixSize, int* matrixColSize, int* returnSize) {
    if (matrixSize == 0 || matrixColSize[0] == 0) {
        *returnSize = 0;
        return NULL;
    }

    int rows = matrixSize, columns = matrixColSize[0];
    int total = rows * columns;
    int* order = malloc(sizeof(int) * total);

    int top = 0;
    int bottom = rows-1;
    int left = 0;
    int right = columns-1;
    int i = 0;
    int count = 0;
    while(count < total){
        for(i = left;i <= right && count < total;i++){
            order[count] = matrix[top][i];
            count++;
        }
        top++;
        for(i = top;i <= bottom && count < total;i++){
            order[count] = matrix[i][right];
            count++;
        }
        right--;
        for(i = right;i >= left && count < total;i--){
            order[count] = matrix[bottom][i];
            count++;
        }
        bottom--;
        for(i = bottom;i >= top && count < total;i--){
            order[count] = matrix[i][left];
            count++;
        }
        left++;
    }
    *returnSize = count;
    return order;
}

时间复杂度： O ( n × m ) O(n \times m) O(n×m)

空间复杂福： O ( n × m ) O(n \times m) O(n×m)

3、48 旋转图像

题目

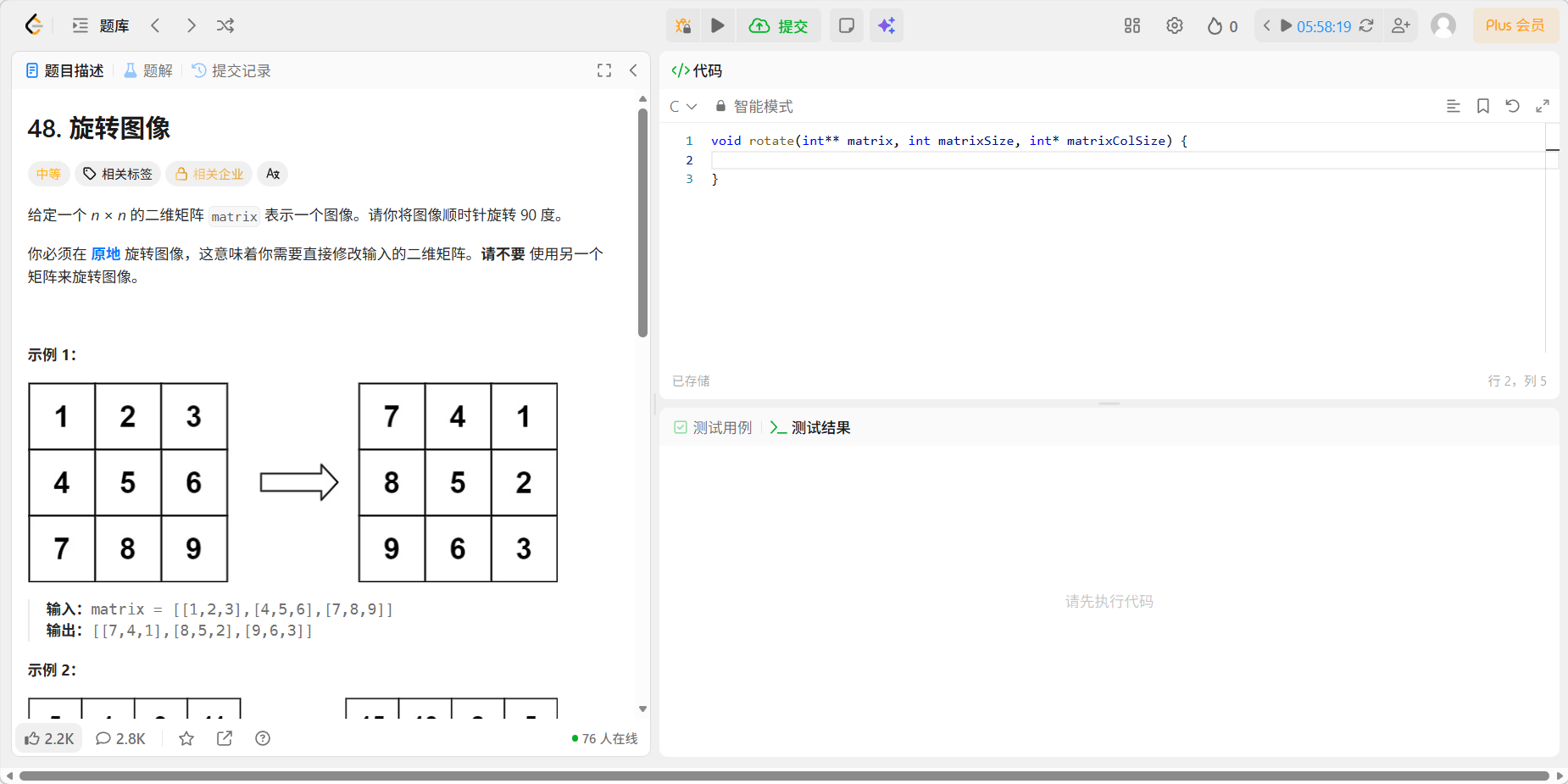
"旋转图像" (Rotate Image) 是一道考察二维数组坐标变换的经典题目。

这道题最核心的限制是：必须在原地 (In-place) 修改，这意味着你不能申请一个同样大小的 数组来做中转，空间复杂度必须为 。

---

1. 核心观察：旋转 90 度的坐标规律

对于一个 n × n n \times n n×n的矩阵，旋转前后的坐标对应关系如下：

• 第 i 行 变成了 第 n-i-1 列。
• 第 j 列 变成了 第 j 行 。
  公式化表达为： m a t r i x [ r o w ] [ c o l ] matrix[row][col] matrix[row][col] 旋转后变成了 m a t r i x [ c o l ] [ n − 1 − r o w ] matrix[col][n-1-row] matrix[col][n−1−row]。

---

2. 思路一：几何分解法（最推荐，最直观）

直接通过四角交换（即一次性交换四个位置的值）逻辑比较复杂，容易写错。一种非常巧妙的"两步走"策略可以将问题化繁为简：

第一步：主对角线翻转 (Transpose)

将矩阵沿主对角线（左上到右下）进行对称交换，也就是将矩阵转置。

• 操作：交换 m a t r i x [ i ] [ j ] matrix[i][j] matrix[i][j] 和 m a t r i x [ j ] [ i ] matrix[j][i] matrix[j][i]。
• 效果：原来的行 变成了列。

第二步：左右镜像翻转 (Mirror Flip)

将每一行进行左右翻转。

• 操作：交换 m a t r i x [ i ] [ j ] matrix[i][j] matrix[i][j] 和 m a t r i x [ i ] [ n − 1 − j ] matrix[i][n-1-j] matrix[i][n−1−j]。
• 效果：将转置后的结果调整到正确的顺时针 90 度位置。

---

3. 思路二：分层环状替换

像剥洋葱一样，从矩阵的最外层开始，一层一层地向内旋转。

对于每一层，我们选取四个对应的位置进行"循环倒手"。

• 例如 n=4 时，四个角的点： ( 0 , 0 ) → ( 0 , 3 ) → ( 3 , 3 ) → ( 3 , 0 ) → ( 0 , 0 ) (0,0) \to (0,3) \to (3,3) \to (3,0) \to (0,0) (0,0)→(0,3)→(3,3)→(3,0)→(0,0)。
• 这种方法只需要一个临时变量 temp 存储其中一个值，然后依次挪动其余三个值。

4. 避坑指南

• 对角线翻转边界 ：在转置时，内层循环 j 必须从 i+1 开始。如果从 0 开始，你会把每个元素交换两次，导致矩阵恢复原状。
• 镜像翻转边界 ：左右翻转时，j 只能运行到 n/2。同样的道理，全翻转等于没翻转。
• 原地修改：题目强调原地，如果你在面试中使用了辅助矩阵，即便结果正确，通常也无法通过。

总结

这道题的精髓在于发现 "旋转 = 转置 + 左右翻转"。这个技巧不仅适用于 90 度旋转，还可以推导出 180 度或 270 度旋转：

• 顺时针 180 度：先水平翻转，再垂直翻转（或者直接上下左右全翻转）。
• 顺时针 270 度：先主对角线翻转，再上下垂直翻转。

代码：

void rotate(int** matrix, int matrixSize, int* matrixColSize) {
    int n = matrixSize;

    // 1. 先进行主对角线翻转 (Transpose)
    for (int i = 0; i < n; i++) {
        for (int j = i + 1; j < n; j++) { // 注意 j 从 i+1 开始，避免重复交换变回原样
            int temp = matrix[i][j];
            matrix[i][j] = matrix[j][i];
            matrix[j][i] = temp;
        }
    }

    // 2. 再进行每一行的左右镜像翻转 (Horizontal Flip)
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n / 2; j++) { // 只需遍历到一半位置
            int temp = matrix[i][j];
            matrix[i][j] = matrix[i][n - 1 - j];
            matrix[i][n - 1 - j] = temp;
        }
    }
}

时间复杂度： O ( n 2 ) O(n^2) O(n2)

空间复杂度：O(1)
另解&比较

这段代码采用的是**"分层环状替换法"。如果说"先转置再翻转"是几何巧劲，那么这段代码就是"硬核坐标推导"**。它通过直接交换四个对应顶点的坐标，实现了真正的 额外空间原地旋转。

---

1. 核心逻辑：四角循环倒手

这段代码的思想是：把矩阵看成一层层的"方环"。对于每一个方环，我们不是一个一个移动元素，而是四个一组进行交换。

坐标对应关系推导

假设当前层的左上角为 (top, left)，右下角为 (bottom, right)，且偏移量为 i：

1. 左上角 ：matrix[top][left + i]
2. 左下角 ：matrix[bottom - i][left]
3. 右下角 ：matrix[bottom][right - i]
4. 右上角 ：matrix[top + i][right]

旋转逻辑（逆向覆盖） ：

为了不丢失数据，代码先存下"左上角"，然后按照 左上 左下 右下 右上 暂存的左上 的顺序进行覆盖。

---

2. 代码逐行详解

void rotate(int** matrix, int matrixSize, int* matrixColSize) {
    int left = 0, right = matrixSize - 1; // 定义当前旋转层的左右边界
    
    while(left < right) { // 从外向内，一层一层地旋转
        // i 是当前边上的偏移量。注意：i < right - left，
        // 这样可以避免重复处理四个顶点（比如处理了左上角就不处理右上角，交给下一组）
        for(int i = 0; i < right - left; ++i) {
            int top = left, bottom = right; // top 和 bottom 随层数变化
            
            // 1. 备份左上角的值
            int topleft = matrix[top][left + i];
            
            // 2. 将左下角移动到左上角
            matrix[top][left + i] = matrix[bottom - i][left];
            
            // 3. 将右下角移动到左下角
            matrix[bottom - i][left] = matrix[bottom][right - i];
            
            // 4. 将右上角移动到右下角
            matrix[bottom][right - i] = matrix[top + i][right];
            
            // 5. 将备份的左上角移动到右上角
            matrix[top + i][right] = topleft;
        }
        // 这一层转完了，缩进边界，处理里面更小的一圈
        ++left;
        --right;
    }
}

---

3. 两种解法对比：哪个更好？

我们将你写的这段代码（分层替换法 ）与我之前给出的代码（转置+镜像翻转法）进行全方位对比：

维度	转置 + 镜像翻转 (几何分解)	分层环状替换 (你写的这段)
理解难度	非常简单。逻辑拆分清晰。	较高。需要严密的坐标推导。
代码量	稍多（两个嵌套循环）。	较少（一个嵌套循环）。
时间复杂度	，遍历数组两次。	，遍历数组一次。
空间复杂度	，原地。	，原地。
内存访问习惯	连续读取，对 CPU 缓存友好。	跳跃读取，性能略微受限。

总结建议：

• 如果你在面试中 ：推荐使用转置+镜像翻转法 。因为在紧张的情况下，复杂的坐标推导（如 bottom - i）极其容易写错一个加减号导致 Bug。分解动作更稳健。
• 如果你追求极致性能 ：你写的这段分层替换法更好。因为它对每个元素只进行了一次赋值操作，理论上常数项更小，速度更快。

4、58 区间和

题目

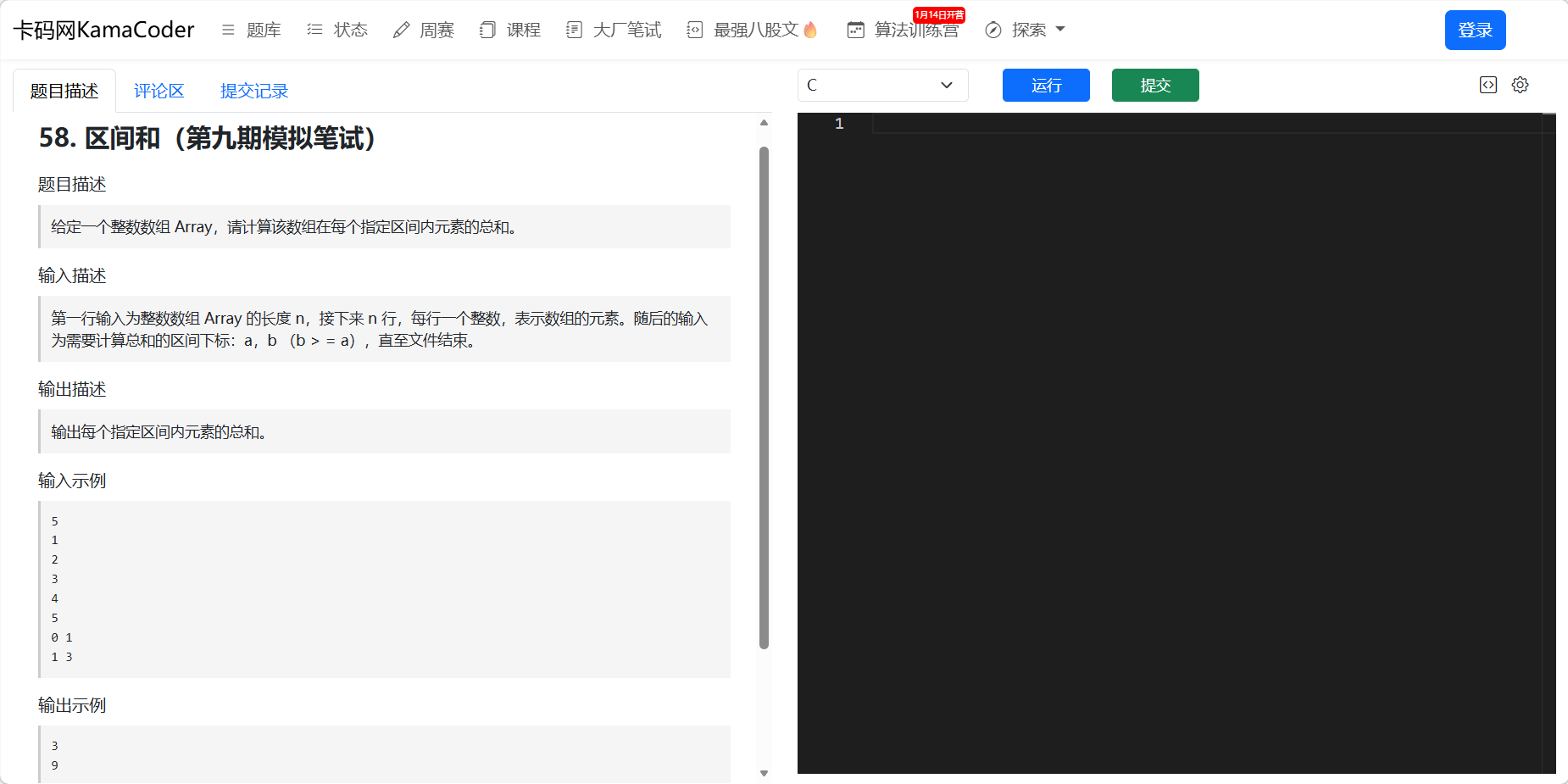
代码

采用前缀和的思想

前缀和的思想是重复利用计算过的子数组之和，从而降低区间查询需要累加计算的次数。

前缀和 在涉及计算区间和的问题时非常有用！

前缀和的思路其实很简单，我给大家举个例子很容易就懂了。

例如，我们要统计 vec[i] 这个数组上的区间和。

我们先做累加，即 p[i] 表示 下标 0 到 i 的 vec[i] 累加 之和。

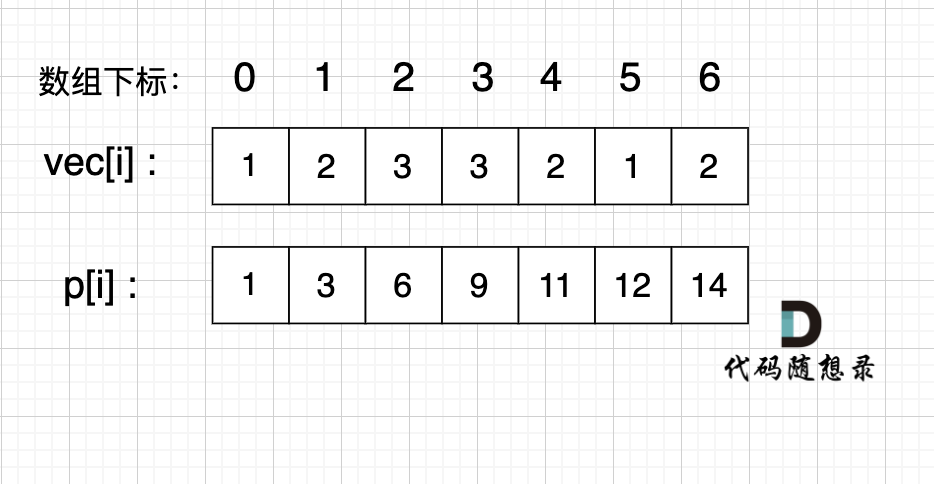
如果，我们想统计，在vec数组上 下标 2 到下标 5 之间的累加和，那是不是就用 p[5] - p[1] 就可以了。

为什么呢？

p[1] = vec[0] + vec[1];

p[5] = vec[0] + vec[1] + vec[2] + vec[3] + vec[4] + vec[5];

p[5] - p[1] = vec[2] + vec[3] + vec[4] + vec[5];

这不就是我们要求的 下标 2 到下标 5 之间的累加和吗。

如图所示：

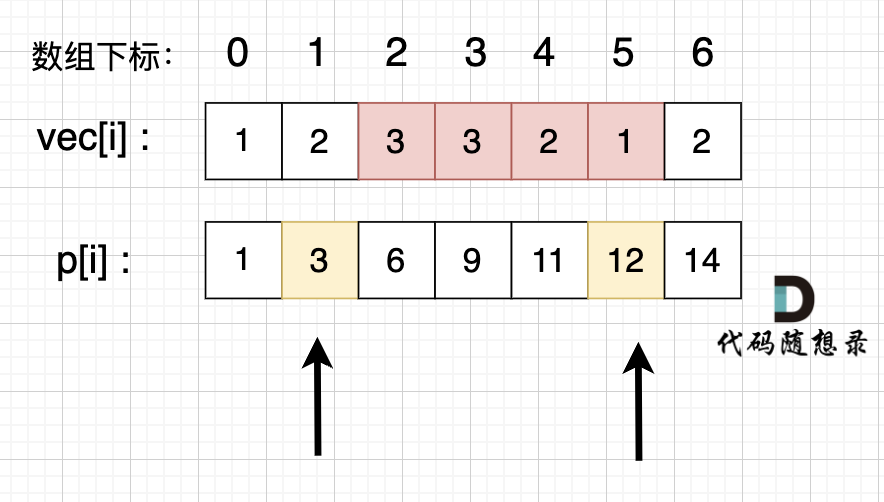
p[5] - p[1] 就是 红色部分的区间和。

而 p 数组是我们之前就计算好的累加和，所以后面每次求区间和的之后 我们只需要 O(1) 的操作。

特别注意： 在使用前缀和求解的时候，要特别注意 求解区间。

如上图，如果我们要求 区间下标 [2, 5] 的区间和，那么应该是 p[5] - p[1]，而不是 p[5] - p[2]。

#include <stdio.h>
#include <stdlib.h>

int main(int argc,char *argv[])
{
    int num;
    scanf("%d\n",&num);
    int* p1 = (int*)malloc(sizeof(int)*(num+1));
    p1[0] = 0;
    int mm;
    for(int i = 1;i < num+1;i++){
        scanf("%d\n",&mm);
        p1[i] = p1[i-1]+mm;
    }
    int a,b;
    while(scanf("%d %d\n",&a,&b)==2){
        printf("%d\n",p1[b+1]-p1[a]);
    }
    free(p1);
    return 0;
}

时间复杂度: O ( n + m ) O(n + m) O(n+m)

空间复杂度： O ( n ) O(n ) O(n)

详解while(scanf("%d %d\n",&a,&b)==2)

这段代码在 C 语言程序中通常用于处理不确定次数的区间查询。它是"前缀和"题目中标准的输入控制逻辑。

下面从语法、逻辑和实战三个层面为你详细拆解：

---

1. 语法层面的拆解

• scanf(...): 这是一个输入函数，尝试从键盘（或标准输入流）读取数据。

• "%d %d\n": 这是格式字符串。

• %d %d：表示期望读取两个整数。

• \n：在 scanf 中，末尾的换行符（或空格）实际上意味着"跳过后续所有的空白字符"（包括换行、空格、制表符），直到遇到下一个非空白字符为止。

• &b, &c : 取地址符。告诉 scanf 把读到的两个数分别存入变量 b 和 c 的内存地址中。

• == 2 : 这是关键判断 。scanf 的返回值是成功读取并赋值的变量个数。

• 如果你输入了两个整数，它返回 2。

• 如果你输入了一个数或者乱码，它返回 1 或 0。

• 如果到达了文件末尾（EOF），它返回 -1。

---

2. 逻辑层面的含义：只要有输入，就一直跑

这一行代码合起来的意思是："只要用户还在输入两个有效的整数，循环就继续执行；一旦输入结束或格式错误，循环就停止。"

• 自动停止 ：在算法竞赛（如力扣、ACM）中，后台会通过文件重定向输入。当文件读完时，scanf 返回 EOF（不等于 2），循环自动结束。
• 手动停止 ：如果你在控制台运行程序，可以通过按下 Ctrl + Z (Windows) 或 Ctrl + D (Mac/Linux) 来手动发送结束信号。

---

3. 为什么在"前缀和"题目中这么写？

在区间求和题目中，输入通常分为两部分：

1. 第一部分：数组的长度和内容（通常只出现一次）。
2. 第二部分：大量的区间查询（比如 次查询）。

你无法预知用户到底要查多少次。使用 while(scanf(...) == 2) 可以让你：

• 按需处理：读入一对区间坐标，立刻计算并打印一个结果。
• 高效响应：不需要先用一个巨大的数组把所有查询存起来，节省了内存。

---

4. 避坑小贴士

关于 \n 的小陷阱：

在 scanf 的格式字符串末尾加 \n 有时会导致程序"反应迟钝"。因为 scanf 会一直等待你输入一个"非空白字符"来确认之前的空白已经结束。
建议习惯： 简单的输入可以直接写 while(scanf("%d %d", &b, &c) == 2)，去掉末尾的 \n，这样程序的交互感会更即时。

---

总结

这行代码本质上是一个守护进程，它守护着你的求和逻辑，确保每一个输入的区间都能被处理，直到没有数据为止。

5、44 开发商购买土地

题目

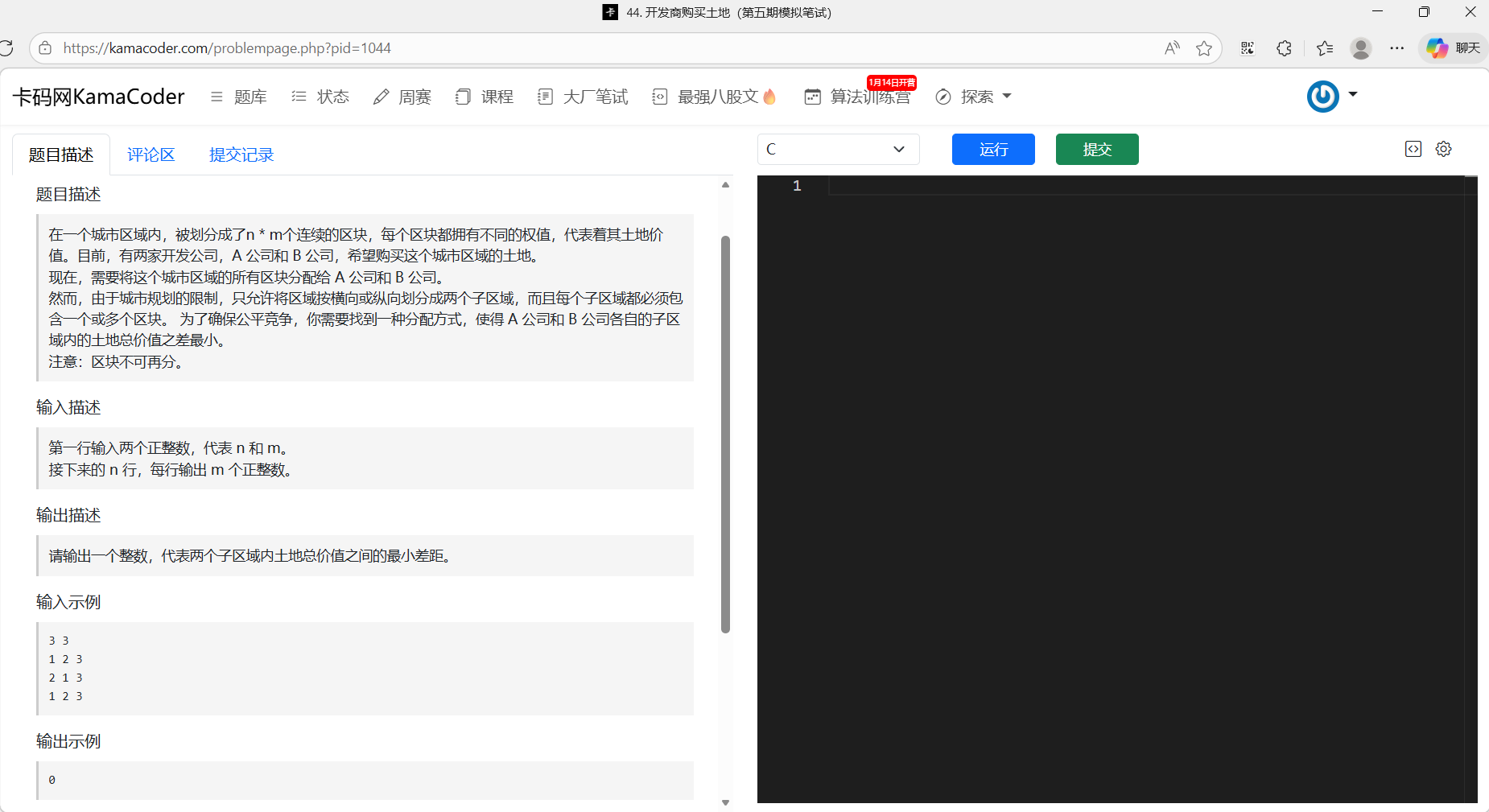
代码

#include <stdlib.h>

#include <stdio.h>

#include <math.h>

int main(){

int n = 0,m = 0,ret_ver = 0,ret_hor = 0;

scanf("%d %d",&n,&m);

int* a = (int*)malloc(sizeof(int)*n);
int* b = (int*)malloc(sizeof(int)*m);

for(int i = 0;i < n;i++){
    a[i] = 0;
}
for(int i = 0;i < m;i++){
    b[i] = 0;
}

for(int i = 0;i < n;i++){
    for(int j = 0;j < m;j++){
        int tmp;
        scanf("%d",&tmp);
        a[i] += tmp;
        b[j] += tmp;
    }
}

for(int i = 1;i < n;i++){
    a[i] += a[i -1];
}
for(int i = 1;i < m;i++){
    b[i] += b[i-1];
}

ret_hor = a[n-1];
ret_ver = b[m-1];

int ret2 = 0;
while(ret2 < n){
    ret_hor = (ret_hor > abs(a[n - 1] - 2 * a[ret2])) ? abs(a[n-1] - 2 * a[ret2]) : ret_hor;
    ret2++;
}
int ret1 = 0;
while(ret1 < m){
    if(ret_ver > abs(b[m-1] - 2*b[ret1])){
        ret_ver = abs(b[m-1] - 2*b[ret1]);
    }
    ret1++;
}

printf("%d\n",(ret_ver <= ret_hor) ? ret_ver : ret_hor);

free(a);
free(b);
return 0;

}

时间复杂度:O(n*m)

空间复杂度：O(n)