目录
[1. 正则化](#1. 正则化)
[2. 分类](#2. 分类)
[1. Logistic regression](#1. Logistic regression)
[2. softmax 多分类](#2. softmax 多分类)
[3. 评估指标](#3. 评估指标)
[3.1 Accuracy、Precision、Recall、F-score](#3.1 Accuracy、Precision、Recall、F-score)
[3.2 AUC-ROC](#3.2 AUC-ROC)
[4. iris实践](#4. iris实践)
[5. SVM](#5. SVM)
[5.1 凸优化复习](#5.1 凸优化复习)
[5.2 对偶问题 & KKT](#5.2 对偶问题 & KKT)
[5.3 非线性可分 - 核函数](#5.3 非线性可分 - 核函数)
[5.4 软间隔 hinge loss](#5.4 软间隔 hinge loss)
1. 正则化

求解lasso时,|w| 在0点处不可微,不可直接用梯度下降法。
法1:次梯度 subgradient
对于凸函数 f 在点 x 处的次梯度 g 是一个支撑超平面对应向量:
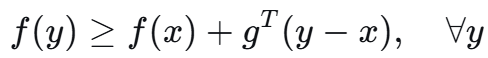
一个 x 可以有多个这样的 g,比如在零点处,-1到1之间的梯度都可以:
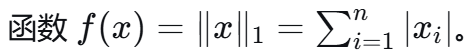
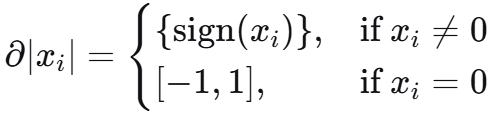
沿着次梯度方向 走一些,如果比之前的最优解好 ,那就更新最优解。
法2:Proximal-GD 近端梯度下降
对光滑部分 g(x) 做梯度下降 ,然后对非光滑部分 h(x) 应用一个特殊的"映射"------近端算子。

法3:Accelerated Proximal Gradient Descent 加速近端梯度下降
在前瞻点 计算梯度,类似于给优化过程增加动量。
2. 分类
1. Logistic regression

损失函数:
(两个反面教材)若 y = kx,y会出现超出 [0, 1];若0-1阶跃函数,不连续
为了很好的近似,使用 sigmoid 函数 1 / 1+exp(-x)
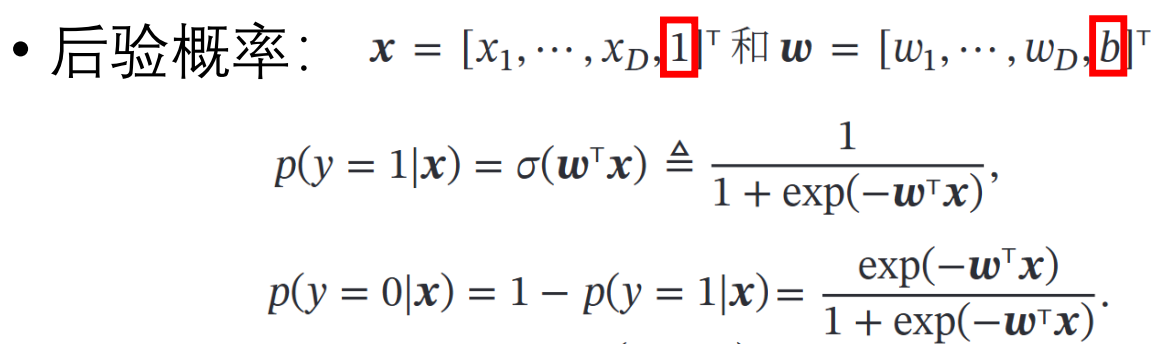
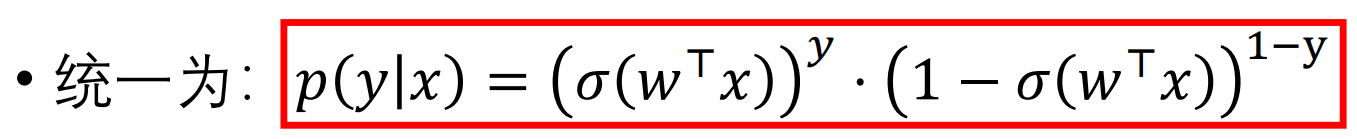
对上面这个 p(y|x) 的乘积,做极大似然估计,再取对数。
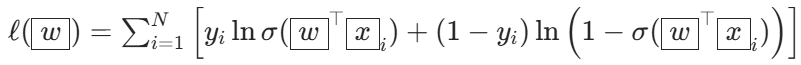
上面可以看做两个二项分布,p(x) = yi,q(x)=σ(w*xi) 的 CrossEntropy 交叉熵。
(下为交叉熵公式)
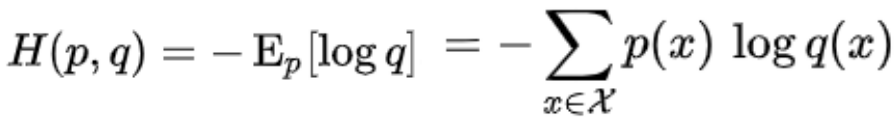
虽然是分类问题,上面是用逻辑"回归" 进行一个 0-1概率预测,概率大的(argmax)即分类为那个。
2. softmax 多分类
作为深度学习分类的输出层。
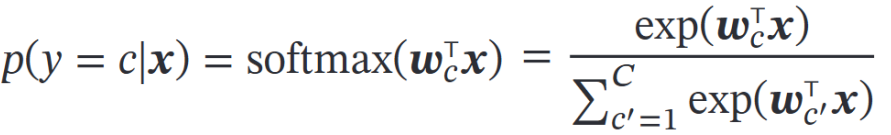
python
def softmax_stable(z):
"""稳定版本:减去最大值"""
z_shift = z - np.max(z)
exp_z = np.exp(z_shift)
return exp_z / np.sum(exp_z)logistic 可看做 softmax 类别为 2 的特例。
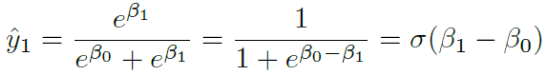
3. 评估指标
不同的评估指标适用于不同的业务场景,核心取决于我们更关注 "避免误判" 还是 "避免漏判"。
以及样本是否存在不平衡问题。
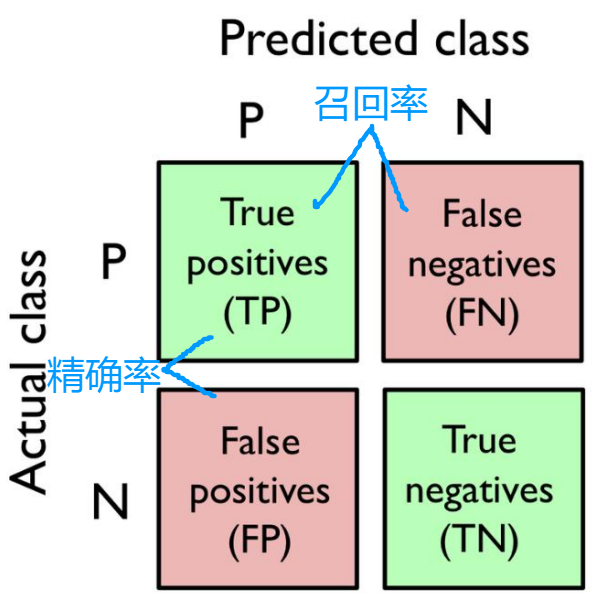
3.1 Accuracy、Precision、Recall、F-score
Accuracy 正确率 TP+TN / 总 ; Error 错误率 FN+FP / 总
Precision 精确率(查准率) -- 预测P的,多少是真P;TP /(TP+FP)
Recall 召回率(查全率) -- 有多少P被找出来了; TP / (TP+FN)
F-score 对 精确率和召回率综合考量。
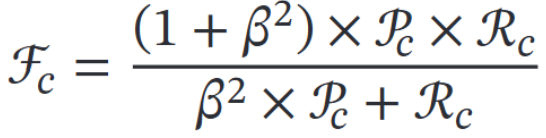
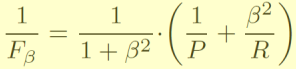
特殊的,β=1时为 F1-score。β越大,召回率 R对结果的影响更大(找罪犯)
β越小,精确率 P对结果的影响更大(商品推荐系统)
例:99%正常;1%病 类别不均匀
如果我所有样本都输出正常,正确率达到99%,对于病例的召回率 0%(啥都没找出来)。
quiz :疾病的诊断系统,判断为肿瘤的阈值提高则:
使得预测为 P 的下降 ,预测为 N 的上升。
对于 Recall 分母是真实标签不变,分子减小,所以减小。
对于 Precision,P整体变少了 ,但是 TP在 P中的比例不能确定。
3.2 AUC-ROC
ROC 为以 ** 假阳性率(FPR)= FP / N**负例中被错误预测为阳性 为横轴,
** 真阳性率(TPR)= TP / P** 正例中被正确预测为阳性 为纵轴绘制的曲线。
AUC(Area Under the Curve) 为 ROC曲线下方的面积。
如下例:统计正例和负例总数(此例均为10)
将 20 个样本按 "模型输出概率" 降序排列,得到如下顺序
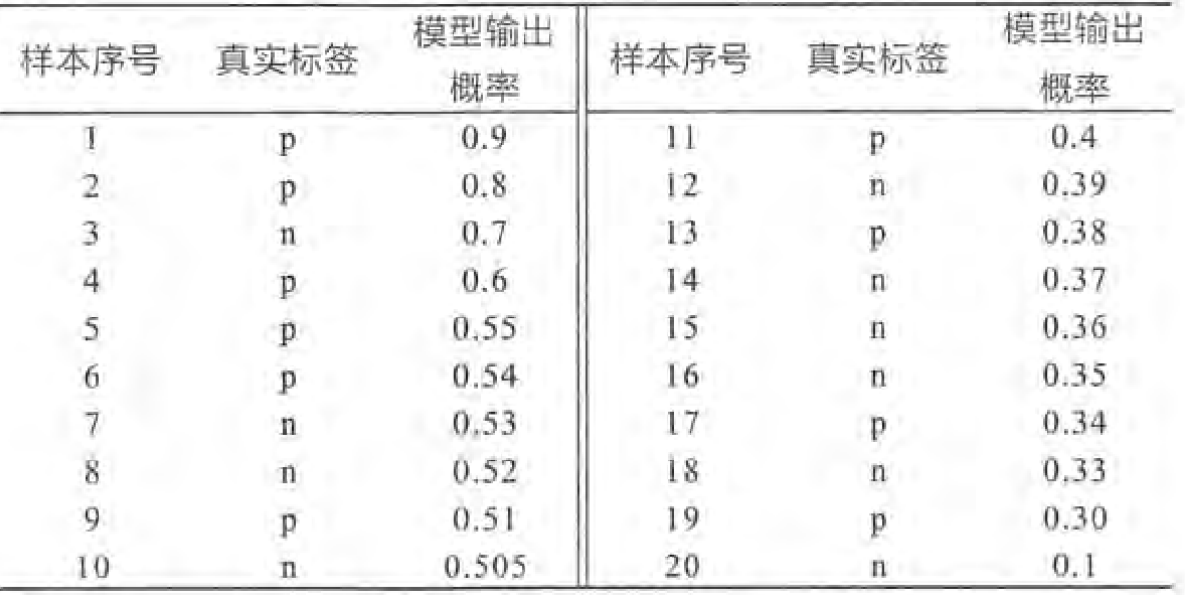
刻画不同的阳性阈值:实现上来讲,真实标签 p :TP++;真实标签 n:FN ++
(每次往上 往右走一小格)都从(0,0)到(1,1)
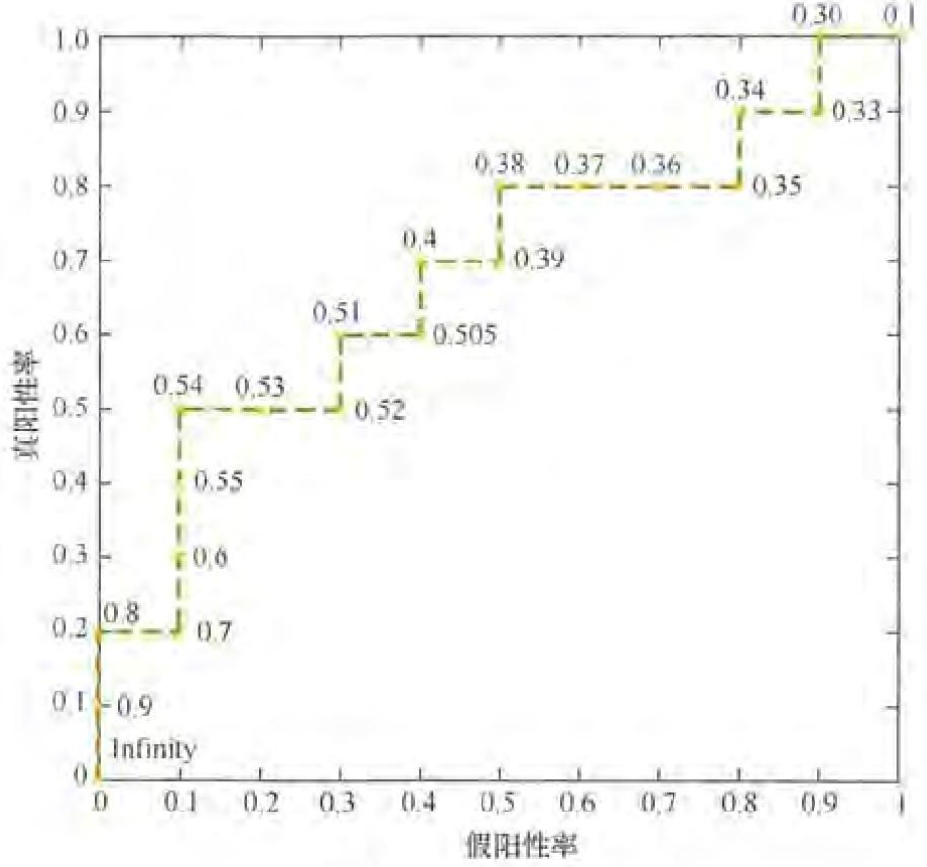
曲线越靠近左上角(0,1),模型性能越好;(最理想情况 先一直往上 再一直往右)
若曲线在对角线(y=x)下方,说明模型性能不如随机猜测,可将预测反转。
AUC本质关心样本预测的排序质量 (正类排在负类前面即可)
python
from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib.pyplot as plt
逻辑回归得到数据
'''
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
# 生成模拟数据
X, y = make_classification(n_samples=1000, n_classes=2, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 训练模型
model = LogisticRegression()
model.fit(X_train, y_train)
'''
y_pred_proba = model.predict_proba(X_test)[:, 1] # 正类的预测概率
# 计算ROC曲线和AUC
fpr, tpr, thresholds = roc_curve(y_test, y_pred_proba)
auc = roc_auc_score(y_test, y_pred_proba)
# 绘制ROC曲线
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, label=f'ROC曲线 (AUC = {auc:.2f})')
plt.plot([0, 1], [0, 1], 'r--', label='随机猜测')
plt.xlabel('假阳性率 (FPR)')
plt.ylabel('真阳性率 (TPR)')
plt.title('ROC曲线与AUC')
plt.legend()
plt.show()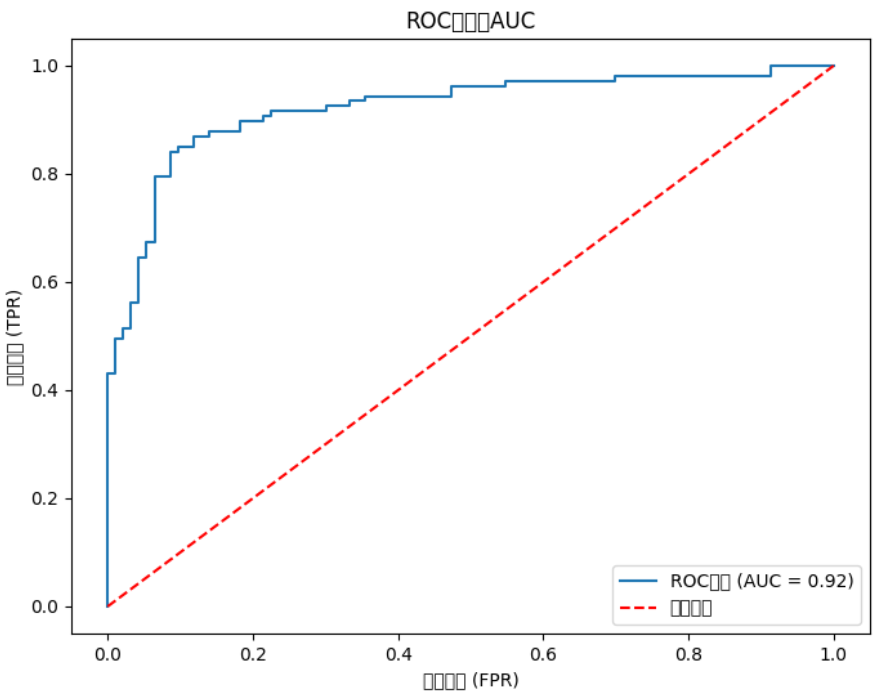
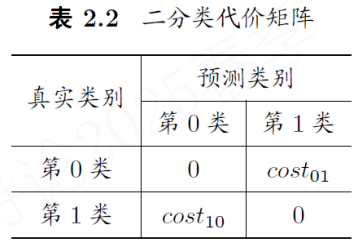
非均等代价犯不同的错误往往会造成不同的损失
4. iris实践
(1)加载数据集
python
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data # 4 个特征:sepal/petal 长度与宽度
y = iris.target # 3 个类别:setosa, versicolor, virginica
print("特征维度:", X.shape)
print("类别名称:", iris.target_names)
# 特征维度: (150, 4)
# 类别名称: ['setosa' 'versicolor' 'virginica'](2)fit + predict + 分类报告 classification_report
python
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report, accuracy_score
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)
clf = LogisticRegression(max_iter=300)
clf.fit(X_train, y_train)
# === 模型预测与评估 ===
y_pred = clf.predict(X_test)
acc = accuracy_score(y_test, y_pred)
print(f"测试集准确率: {acc:.4f}\n")
# 测试集准确率: 0.9333
print("分类报告:\n", classification_report(y_test, y_pred, target_names=iris.target_names))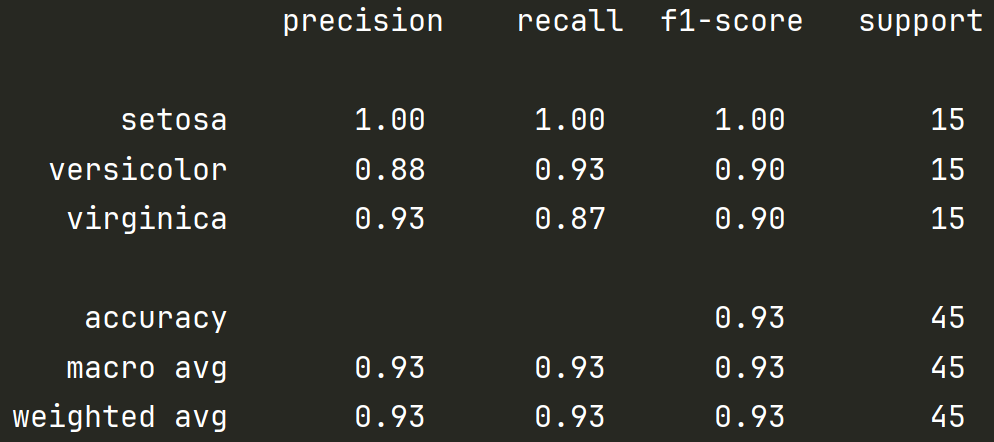
最右边 support 代表每类样本个数。
前三行是三个种类的花,分别预测的 精确率 / 召回率 / f1-score
macro avg,每列的直接平均;weighted avg,每列对样本数的加权平均。
(3)混淆矩阵可视化
python
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import confusion_matrix
# === 混淆矩阵可视化 ===
cm = confusion_matrix(y_test, y_pred)
sns.heatmap(cm, annot=True, cmap="Blues", fmt="d",
xticklabels=iris.target_names, yticklabels=iris.target_names)
plt.xlabel("Prediction")
plt.ylabel("True Label")
plt.title("Iris Confusion Matrix")
plt.show()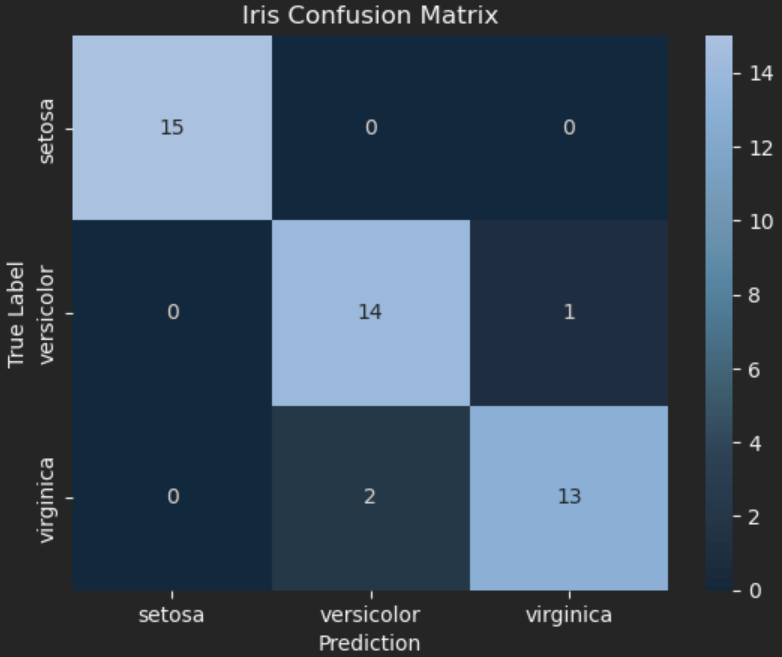
可见两个 2类 被错误分类为了 3类;一个 3类被错误分类为了2类。
(4)softmax 参数矩阵 W ;每个类别的每个特征对应权重。
python
import pandas as pd
coef_df = pd.DataFrame(clf.coef_, columns=iris.feature_names, index=iris.target_names)
print("\n每个类别对应的权重(Softmax回归参数矩阵W):")
display(coef_df.round(3))
5. SVM
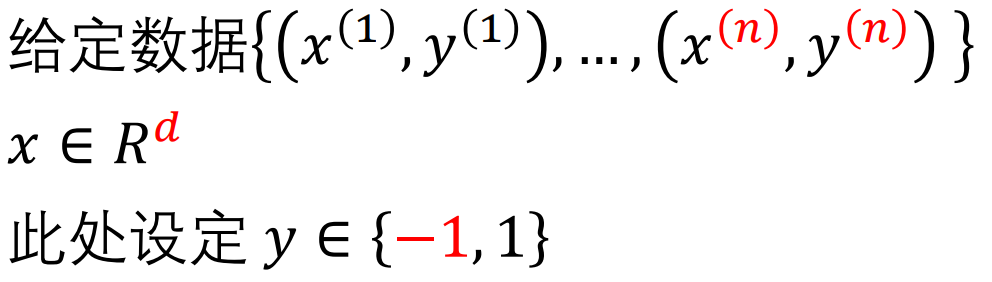
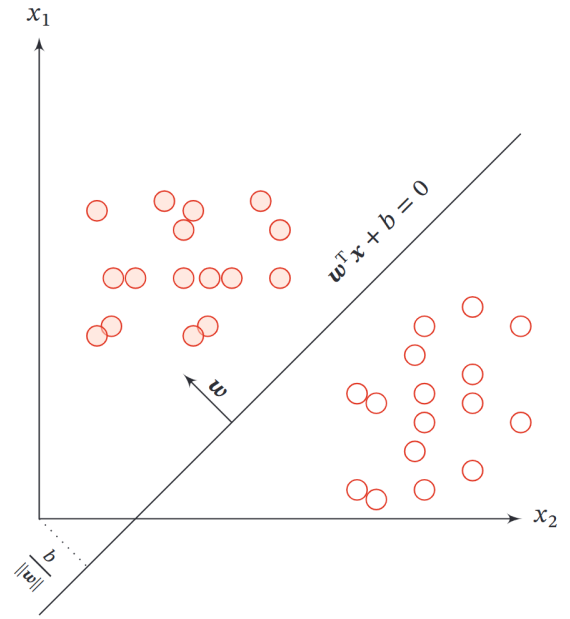
找一个平面把两类点分开,间隔最大。
关于"间隔" margin -> 点到直线的距离推导
令距离为 d,找投影点。 w^T x + b = 0 对应垂直方向为 w。


由于超平面 wx+b = 0;对 w和b 同时乘以一个系数,超平面不变。
所以可令 |w| = γ 问题可转换为
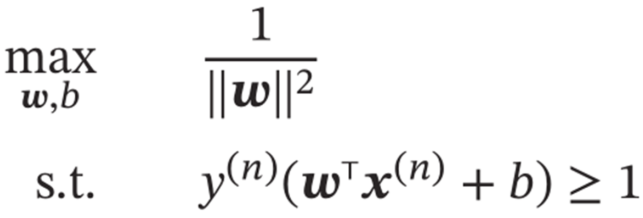 =>
=> 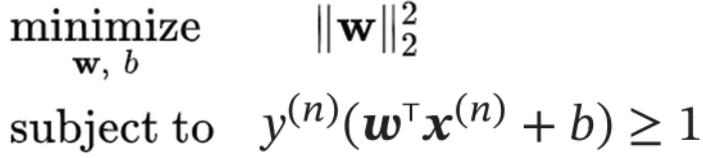
5.1 凸优化复习
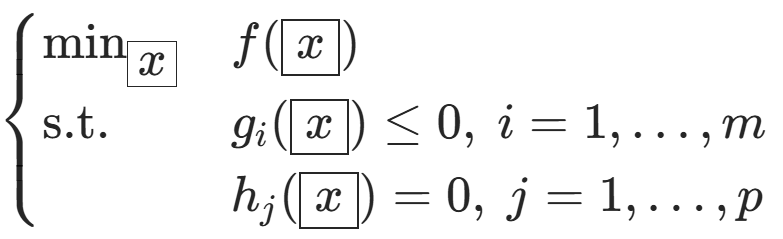
其中\(f, g_i\)是凸函数,\(h_j\)是仿射函数),其拉格朗日函数为:
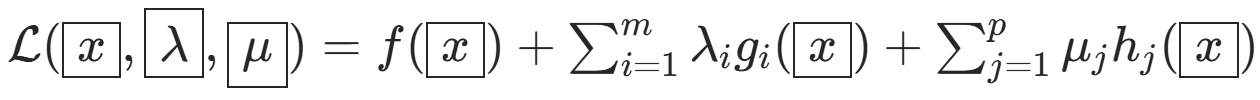
对偶问题定义为
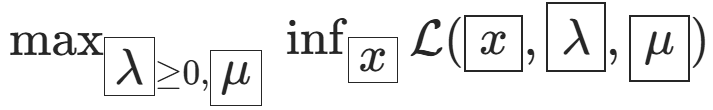
弱对偶性:对偶问题的最优值 ≤ 原问题的最优值(凸优化问题都满足)
强对偶性:+ Slater 条件,对偶间隙 = 0;即 对偶问题的最优值 = 原问题的最优值
Slater 条件:存在 x :仿射约束可行,非线性约束严格满足,等式约束自然满足。
对应到 SVM中:
满足 目标函数凸函数&仿射约束。
存在 w,b 满足所有的约束,即点是线性可分的情况下,满足强对偶性。
KKT条件的直观理解:
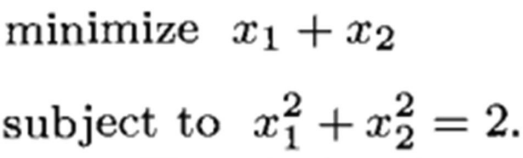
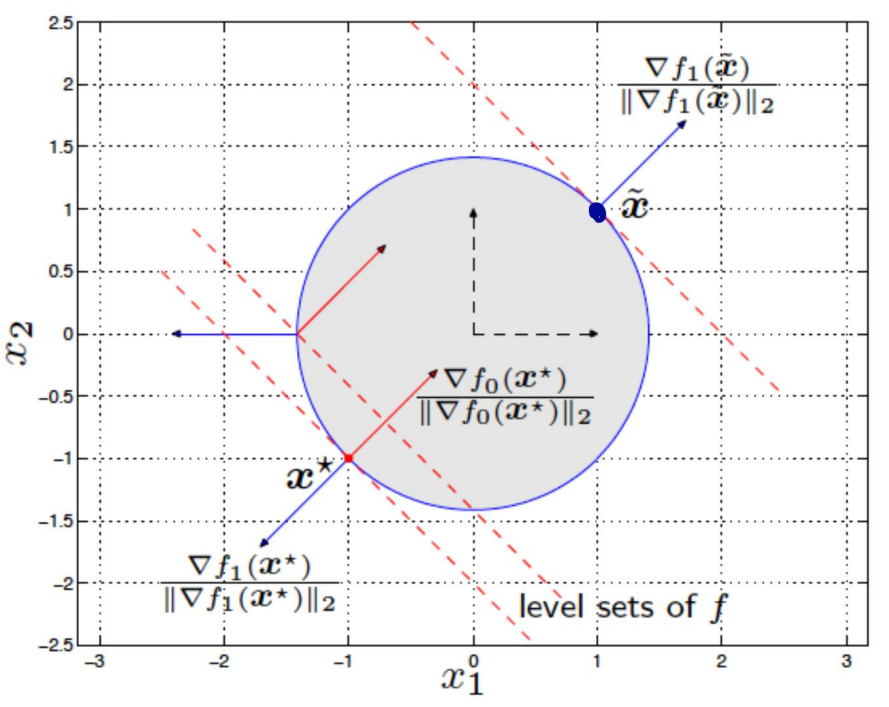
最优点相切,条件约束方向 与 目标函数梯度方向 同向。

5.2 对偶问题 & KKT
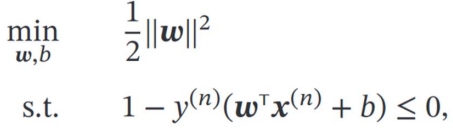
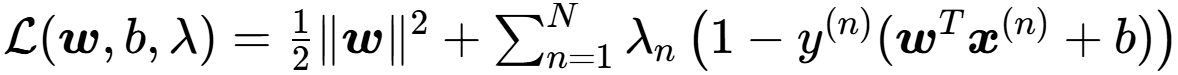
拉格朗日乘子分别对 w和b 求导得:
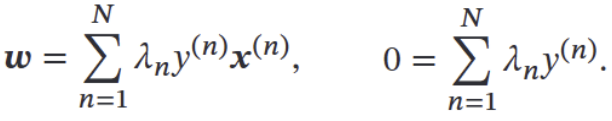
代入得拉格朗日对偶问题:
两个和式相乘,等于所有项两两相乘后的和
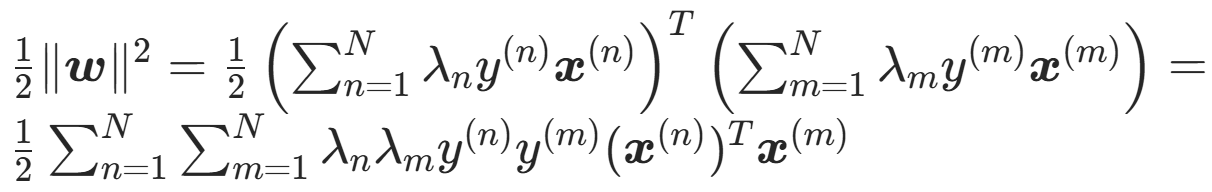
b 前的系数为 0;消掉
后一项,因为 w 也是一个累加,合并之后即为一个二维求和。
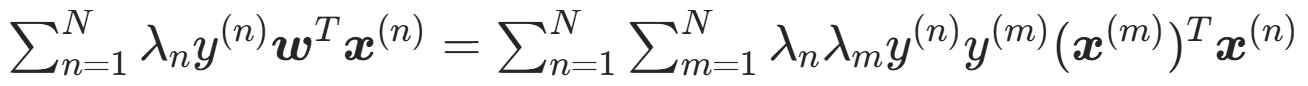
最终的对偶问题为
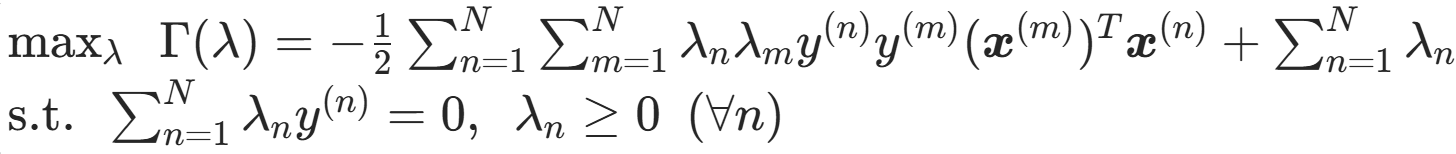
反证存在 λ ≠ 0:(所有 λ=0 则 w* = 0。要分正负 b * y ≥ 1;y有±1 ,b不能都满足)
算出 λ后代入得 w*;再找一个支持向量(离决策平面最近的点)
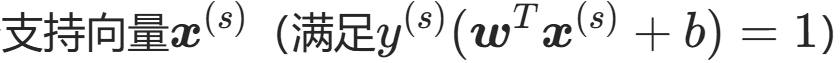 代入求得 b。
代入求得 b。
新数据点分类:看符号正负。
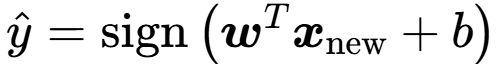
5.3 非线性可分 - 核函数
通过映射 φ,在新空间中线性可分。
对偶问题中,只需要知道映射的内积是多少。
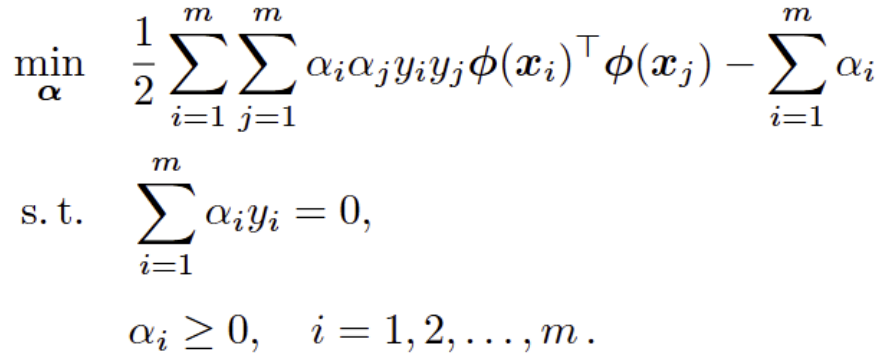
假设存在一个低维函数,执行先映射再内积。
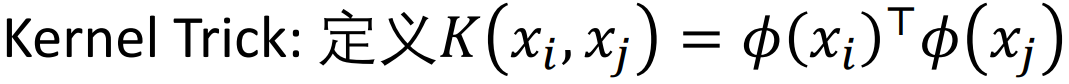

常用高斯核 RBF:Radial basis function
(但是对核需要调参)
5.4 软间隔 hinge loss
允许部分分类错误,并给损失。
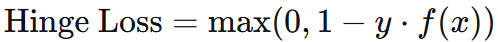
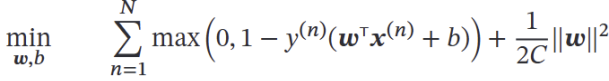
类似正则化:前者为误差项,后者为模型复杂度正则化项。
https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html
sklearn.svm 参数
-
C (float): 正则化参数,与正则化强度成反比,必须为正数
-
kernel (str/callable): 核函数类型
-
degree (int): 多项式核的阶数(仅对 'poly' 核有效)
-
gamma (str/float): 核系数 单个训练样本的影响范围,用于 'rbf', 'poly', 'sigmoid'
-
'scale': 使用 1/(n_features * X.var())
-
'auto': 使用 1/n_features
-
浮点数:必须非负
-
python
from sklearn.svm import SVC
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
# 创建数据
X, y = make_classification(n_samples=100, n_features=4, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
# 创建 SVC 模型
svc = SVC(
C=1.0,
kernel='rbf',
gamma='scale',
probability=True,
random_state=42
)
# 训练模型
svc.fit(X_train, y_train)
# 访问输出属性
print("支持向量数量:", svc.support_vectors_.shape[0])
print("类别标签:", svc.classes_)