目录
前言
从本篇开始,将进入一个大模型的专栏系列,本系列将涵盖以下方向的内容:
人工智能的理论基础、模型的预训练、模型的微调、模型的优化、模型的部署、实战场景等等。从小白的视角出发,从0开始系统性的养成一个大模型工程师。一起加油!
人工智能的本质是函数
"Functions describe the world"
函数是用来描述整个世界的语言,因为整个世界万物的协作都是相互动作之间的反馈,反馈就是应对不同输入给出的输出,所以我们可以用函数来描述世界万物。只是根据场景的不同,这个函数或简单或复杂。
所谓的人工智能其实就是函数,一个复杂函数,一个用来解决具体问题的复杂函数。比如用来视图的AI,输入是图片,输出是识别结果,图片和结果之间的函数关系就是这个视图AI;再比如对话AI,输入是问题,输出是回答,问题和回答之间的函数关系就是这个对话AI。
如何找到这个函数?
人工智能本质上就是用来解决某一个问题的函数,这个函数该如何找到?其实主要是靠猜,这也是整个人工智能的训练过程。
举个例子:
输入和输出的关系是一个一元函数的关系,假设这个一元函数y=wx+b,如何知道这个w和b的值是多少喃?很多人一看,这太简单了,把值带进去解一个二元一次函数嘛,超简单对吧。但是不能这样做,只能通过不停的去试w和b的值,从而找到w和b的值,如下图所示。
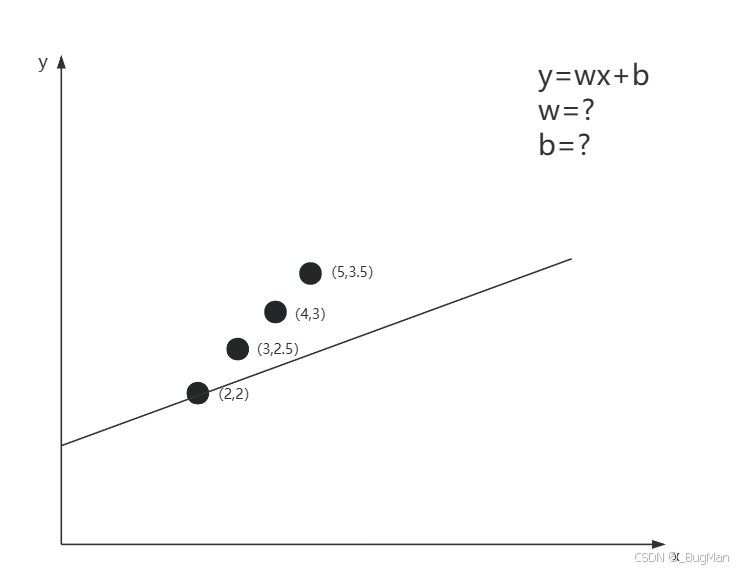
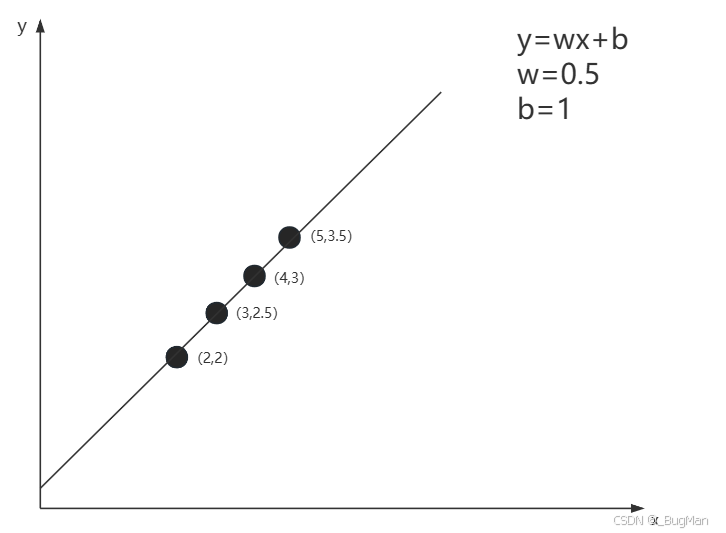
这时候大多数人就有个疑问:
【question】为什么不直接列方程求解?要快的多啊
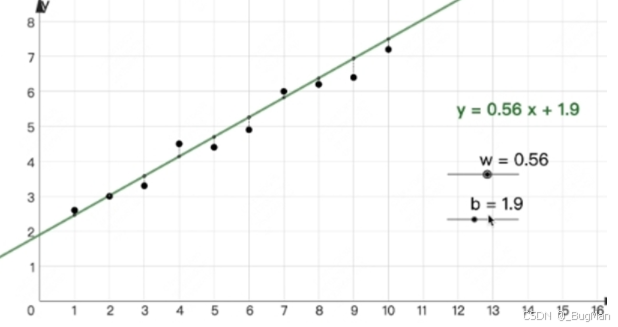
【answer】因为绝大多数情况下,现实中的输入输出受很多"噪音"的影响,没办法找出一个绝对精准的函数来,只能找出一个近似值,比如下面这种:
函数和神经网络的关系
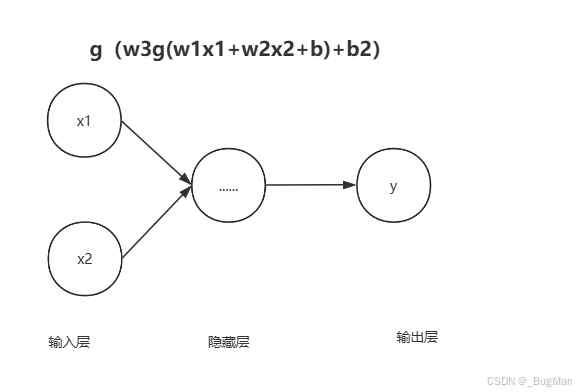
前面我们说了这个函数可能不是百分之百准确的这个问题,除了这个问题外,还有一个问题就是这条函数的线段绝大多数时候都不是直的。因为现实世界中输入和输出绝大多数时候不是简单的线性关系,这个时候就没办法用简单的线性函数来描述,怎么办?这个时候就要引入激活函数,当输入和输出不是线性关系的时候,需要在外层套一个非线性的函数作为激活函数,让这条线弯曲起来,比如在外层套一个sin,cos,平方等等。
f(x)=g(wx+b)
上面的g就是激活函数。
理论上可以在外面套无数层激活函数使得函数呈现出任意的非线性变换:
f(x)=g2(g1(wx+b)+w1)+w2

这种线性变换外面不停套激活函数,每一层激活函数就可以抽象成一个神经元,其输入是来自上一层的输出,这也就是神经网络,非输入输出的中间过程的层叫做隐藏层: