目的:
对来自两个总体的独立样本,推断两个总体的均值是否存在显著差异。
前提:
-
独立:两组数据相互独立,互不相关。比如抽取样本为某校男生和女生平均上网时间
-
正态:即两组样本来自的总体符合正态分布
-
方差齐性:即两组方差相等(不是指严格相等)
例子:
评价两位老师的教学质量,试比较其分别任教的一班和二班(设一班和二班的原成绩相近,不存在差别)考试后的成绩是否存在差异?
数据如下:
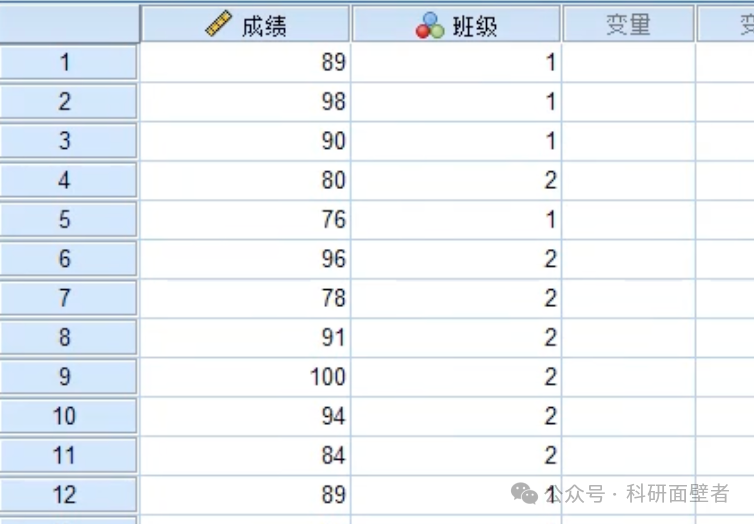
变量属性:
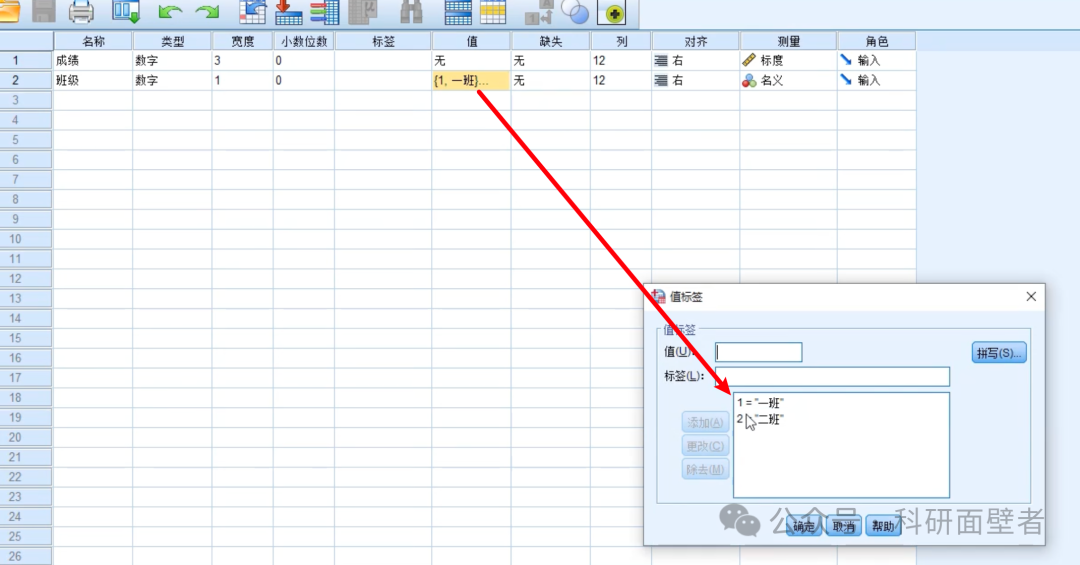
进行独立样本T检验
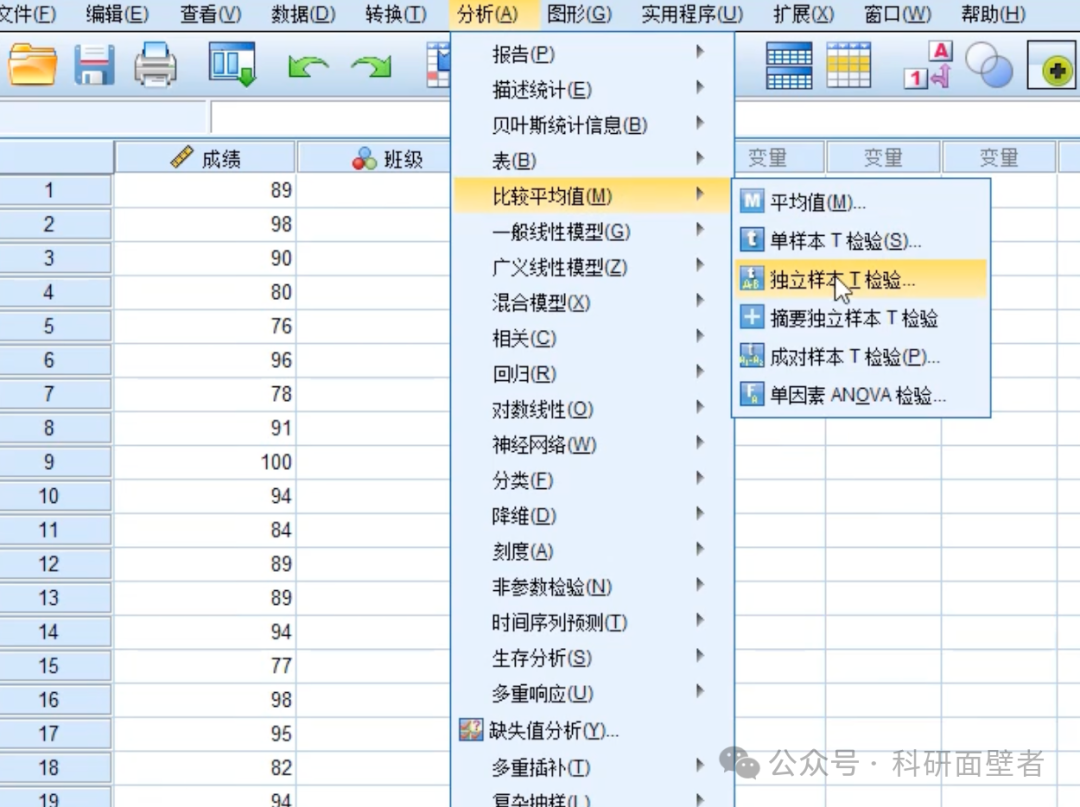
设置:
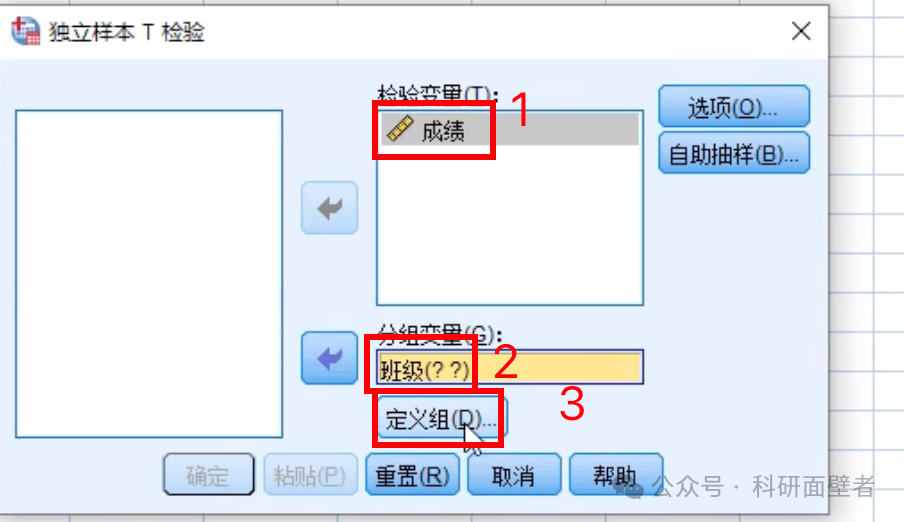
定义组:
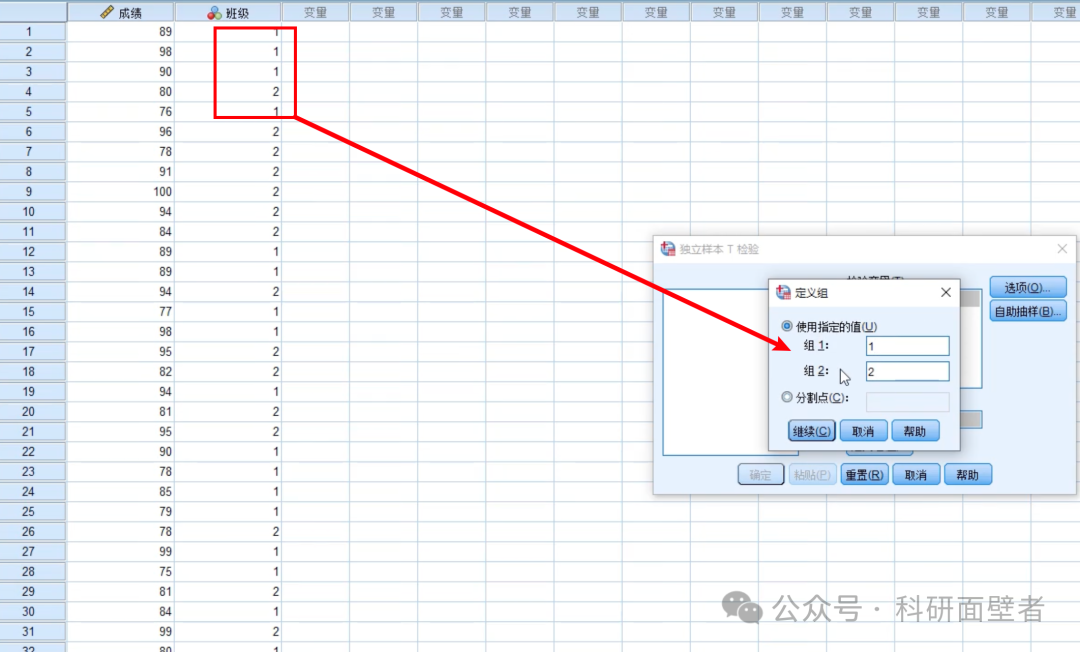
如果班级比较多,则可以选择如下方式,进行分割,令小于分割点的是一部分,大于分割点的是另一部分:
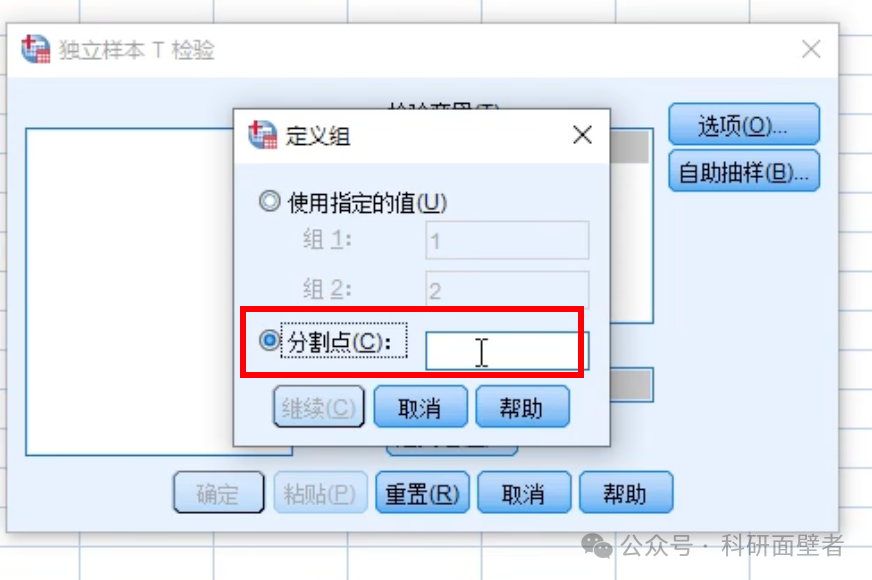
点击继续:
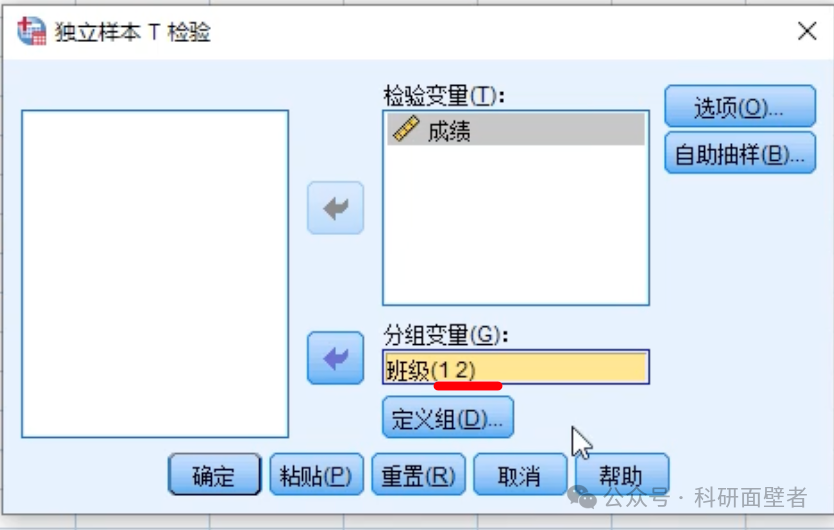
选项菜单,置信区间保持默认就行:
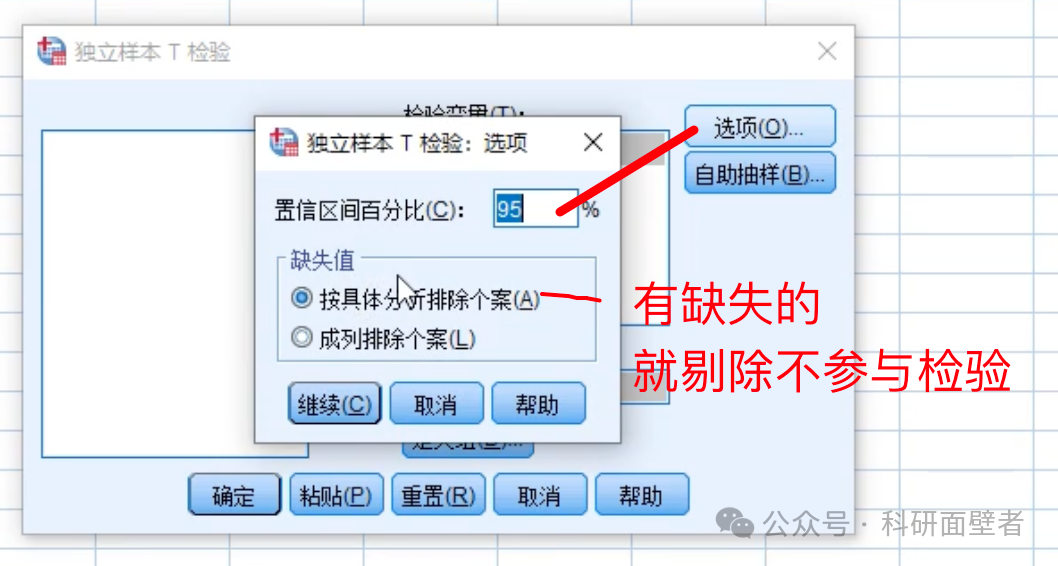
点确定:
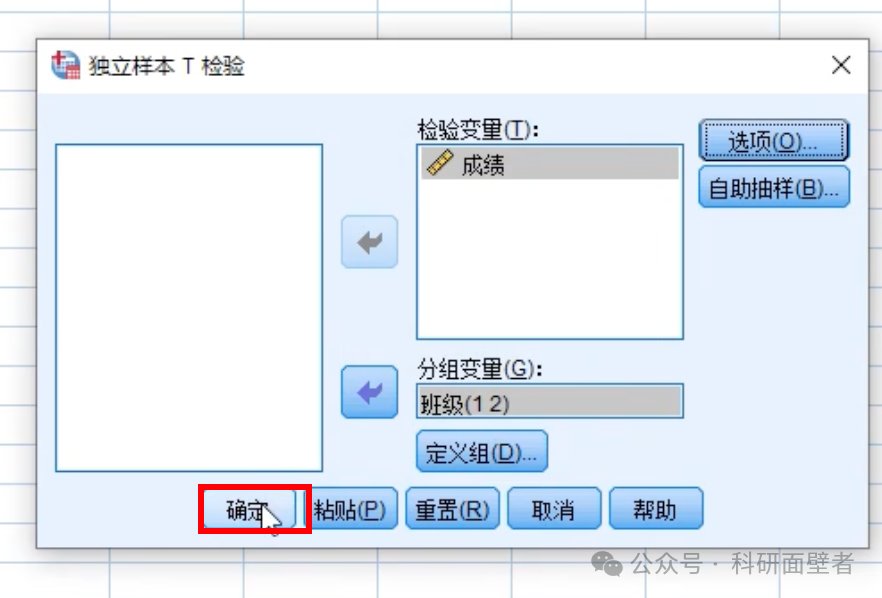
检验结果如下:
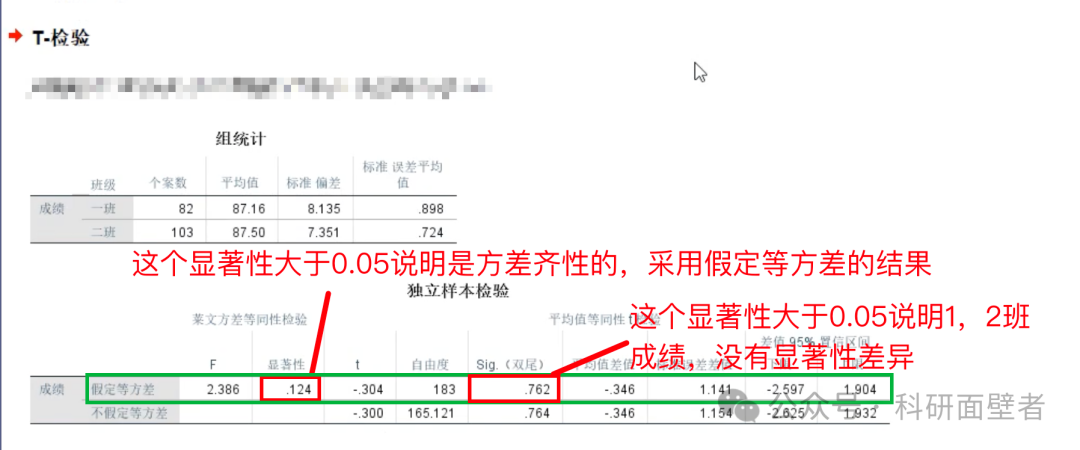
结论
从组统计 中可以看到一班和二班的统计个案数、平均成绩、标准偏差等。从独立样本检验 中看到有有假定等方差和不假定等方差两行。我们首先看方差齐性检验的显著性,发现是大于0.05的,说明是保留假设检验,因此看假定等方差 这行统计结果。平均值等同性t检验中t的值是-0.304,自由度是183,显著性值是0.762大于0.05,说明一班和二班的成绩不存在显著差异,两位老师的教学水平差不多。
至此,本期教程就结束啦,希望对同学有帮助~
后续会持续分享Origin/Matlab/Python绘图教程和配色,SPSS数据分析等
更多免费教程和软件,【SPSS 27安装过程】: