【0基础学算法】前缀和刷题日志（三）：连续数组、矩阵区域和

文章目录

连续数组（medium）

题目链接

525. 连续数组

题目描述

解法

本题解题关键在于将原数组的0转化-1

此时问题就简化为：求最长和为0的子数组的长度

该题与求和为k的子数组就非常类似了

此题的算法原理上篇文章有讲解：0基础学算法】前缀和刷题日志（二）：前缀和与子数组的心动瞬间

但还是有很多细节需要注意

前缀和+哈希表

设i 为数组中的任意位置，⽤sum[i] 表⽰[0, i] 区间内所有元素的和（前缀和）
在区间[0, i-1]中，有多少个前缀和为sum[i]，那么就有多少个符合条件的以i为结尾的子数组。
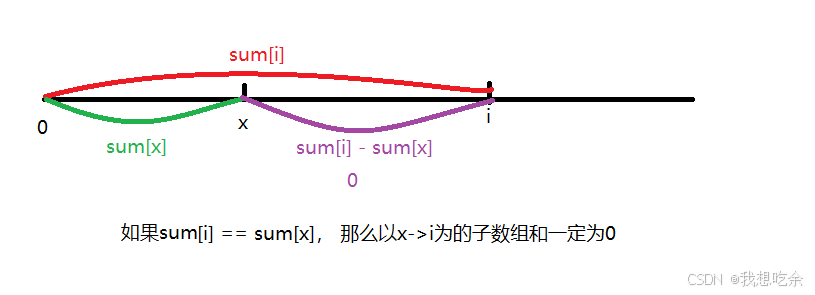
这里哈希表中存什么？
key存前缀和，value存下标（用于求子数组长度）

细节问题：

前缀和存入哈希表的时机
前缀和使用完后，再存入哈希表
如果有重复的（等值的）前缀和需要存入哈希表，如何选取？
选择先存入的前缀和，因为遍历数组从左往右，前缀和越靠左，得到的目标子数组就越长。
边界情况：如果前缀和为0，该如何？
预先存入哈希表，下标设置为-1。即hash[0] = -1
长度如何计算？

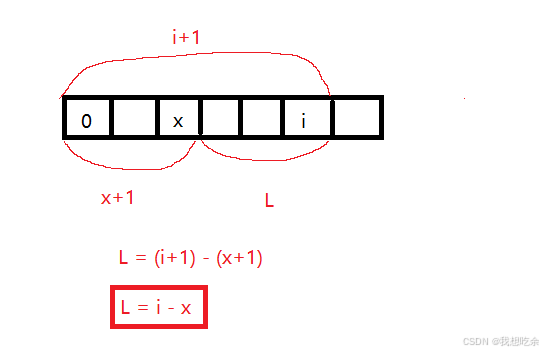
代码（C++）：

cpp 复制代码

class Solution {
public:
    int findMaxLength(vector<int>& nums) {
        //问题转化：求最长和为0的子数组
        int sum = 0, ret = 0;
        unordered_map<int, int> hash;
        //边界情况：sum == 0
        hash[0] = -1;
        for(int i = 0; i < nums.size(); ++i)
        {
            //0->-1
            sum += nums[i] == 0 ? -1 : 1;//当前前缀和
            if(hash.count(sum)) ret = max(ret, i - hash[sum]);
            else hash[sum] = i;
        }
        return ret;
    }
};

矩阵区域和（medium）

题目链接

1314. 矩阵区域和

题目描述

解法

二维前缀和

二维数组前缀和递推公式：

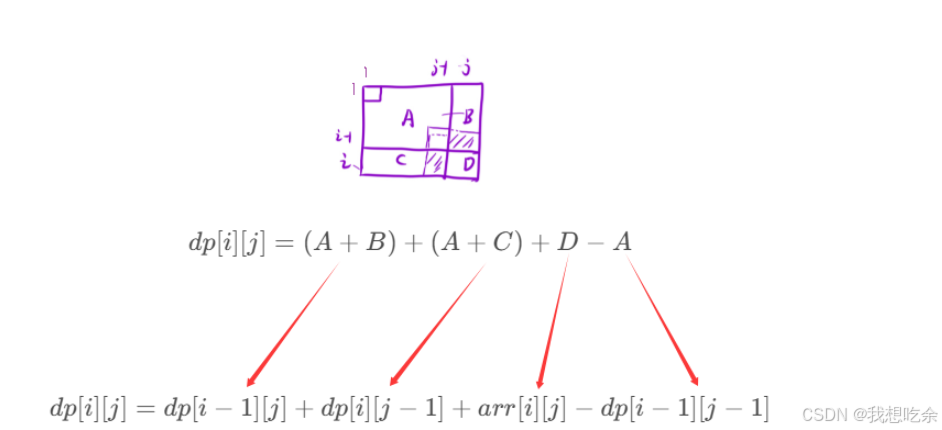
算法原理：

使用前缀和求区域和方式如下：
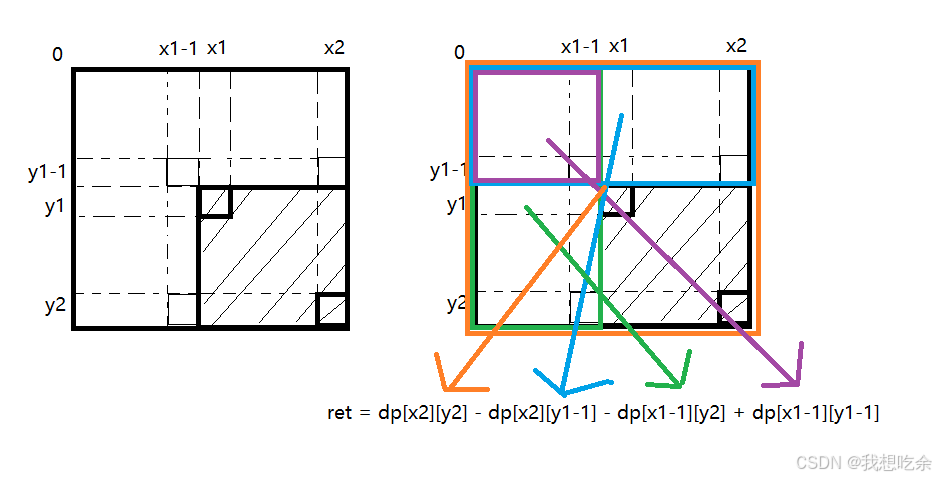
也就是说，只需确定所求目标区域的左上角和右下角元素坐标即可利用前缀和矩阵求得一个区域和
求左上角和右下角元素的坐标：

可得：
- x1 = max(0, i-k)
- y1 = max(0, j-k)
- x2 = min(n-1, i+k)
- y2 = min(m-1, j+k)
下标映射关系

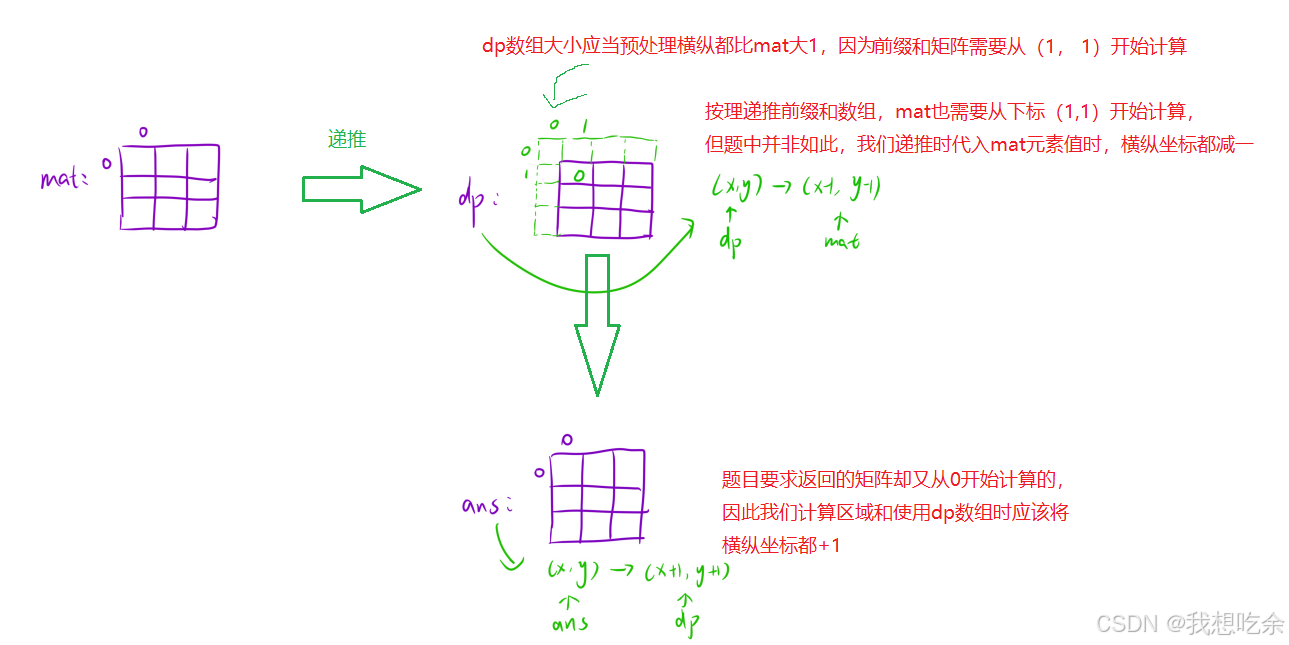
因此我们递推dp时：mat[i][j]改为mat[i-1][j-1]
求区域和时：
- x1 = max(0, i-k)+1
- y1 = max(0, j-k)+1
- x2 = min(n-1, i+k)+1
- y2 = min(m-1, j+k)+1

代码（C++）:

cpp 复制代码

class Solution {
public:
    vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
        int n = mat.size(), m = mat[0].size();
        //先预处理一个前缀和矩阵
        vector<vector<int>> dp(n+1, vector<int>(m+1));
        for(int i = 1; i < n+1; ++i)
        {
            for(int j = 1; j < m+1; ++j)
                dp[i][j] = dp[i][j-1] + dp[i-1][j] - dp[i-1][j-1] + mat[i-1][j-1];
        }
        //使用前缀和矩阵求区域和
        vector<vector<int>> answer(n, vector<int>(m));
        for(int i = 0; i < n; ++i)
        {
            for(int j = 0; j < m; ++j)
            {
                int x1 = max(0, i-k) + 1;
                int y1 = max(0, j-k) + 1;
                int x2 = min(n-1, i+k) + 1;
                int y2 = min(m-1, j+k) + 1;
                answer[i][j] = dp[x2][y2] - dp[x2][y1-1] - dp[x1-1][y2] + dp[x1-1][y1-1];
            }
        }
        return answer;
    }
};

前缀和完~