算法题——图论

98.可达路径

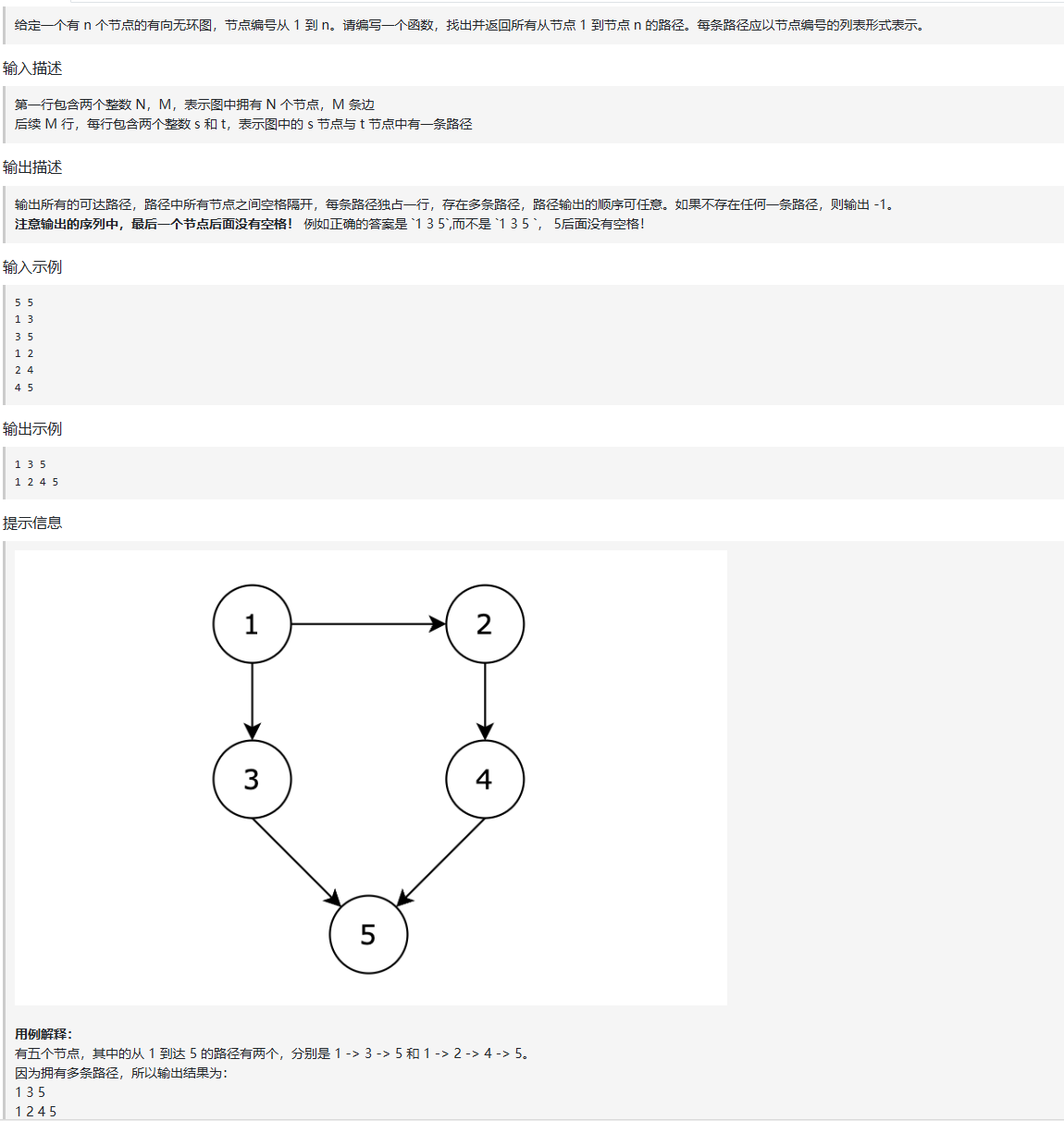
使用深度优先遍历进行递归

邻接矩阵存储，进行深度优先遍历

java 复制代码

import java.util.*;
 
public class Main{
    static List<List<Integer>> res = new ArrayList<>();
 
    static List<Integer> path = new ArrayList<>(); 
 
    public static void dfs(int[][] graph, int cur, int target){
        if(cur==target){  //如果当前遍历的就是目标节点，则说明找到了一条路径
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i=1;i<=target;i++){ //遍历当前节点对应的邻接矩阵的一行，与当前节点相连的节点可以加入路径
            if(graph[cur][i]==1){
                path.add(i);
                dfs(graph, i, target);
                path.remove(path.size()-1);
            }
        }
    }
 
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
 
        int[][] graph = new int[n+1][n+1]; //定义邻接矩阵
        while(m--!=0){
            int s = sc.nextInt();
            int t = sc.nextInt();
            graph[s][t] = 1;  //对应边的位置
        }
        path.add(1);  ////题目要求从1开始，所以path第一个元素必须是
        dfs(graph, 1, n);
 
        if(res.isEmpty()) System.out.println(-1); //处理输出
        for(List<Integer> list : res){
            for(int i=0;i<list.size()-1;i++){
                System.out.print(list.get(i) + " ");
            }
            System.out.println(list.get(list.size()-1));
        }
    }
}

邻接表存储，进行深度优先遍历

java 复制代码

import java.util.*;

public class Main {
    static List<List<Integer>> res = new ArrayList<>();
    static List<Integer> path = new ArrayList<>();

    static void dfs(List<LinkedList<Integer>> graph, int cur, int target) {
        if (cur == target) {
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i : graph.get(cur)) { //遍历当前节点对应的链表，链表上的节点可以加入路径
            path.add(i);
            dfs(graph, i, target);
            path.remove(path.size() - 1);
        }
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        List<LinkedList<Integer>> graph = new ArrayList<>(n + 1);//定义邻接表
        for(int i=0;i<=n;i++){  //初始化邻接表的边表（链表）
            graph.add(new LinkedList<Integer>());
        }
        while (m-- > 0) {
            int s = sc.nextInt();
            int t = sc.nextInt();
            graph.get(s).add(t); //将边的信息加入邻接表
        }
        path.add(1); //题目要求从1开始，所以path第一个元素必须是1
        dfs(graph, 1, n);
        if (res.isEmpty()) System.out.println(-1); //处理输出
        for (List<Integer> list : res) {
            for (int i = 0; i < list.size() - 1; i++) {
                System.out.print(list.get(i) + " ");
            }
            System.out.println(list.get(list.size() - 1));
        }
    }
}

要熟悉邻接矩阵和邻接表存储图的过程，熟悉dfs遍历的写法

99.计数孤岛

本题思路是用遇到一个没有遍历过的节点陆地，计数器就加一，然后把该节点陆地所能遍历到的陆地都标记上。

在遇到标记过的陆地节点 和海洋节点的时候直接跳过。这样计数器就是最终岛屿的数量

深度优先遍历的写法：

java 复制代码

import java.util.*;

public class Main{
    public static int[][] dir = {{0,-1}, {0,1}, {-1,0}, {1,0}}; //四个方向
    public static void dfs(boolean[][] visited, int[][] graph, int x, int y){
        //获取四个方向的坐标
        for(int i=0;i<4;i++){
            int nextX = x+dir[i][0];
            int nextY = y+dir[i][1];
            if(nextX<0 || nextY<0 || nextX>=graph.length || nextY>=graph[0].length) continue;
            if(!visited[nextX][nextY] && graph[nextX][nextY]==1){
                //该位置未被访问过，且为陆地
                visited[nextX][nextY] = true;
                dfs(visited, graph, nextX, nextY);
            }
        }
    }
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        int[][] graph = new int[n][m];
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                graph[i][j] = sc.nextInt();
            }
        }
        boolean[][] visited = new boolean[n][m];
        int res = 0;
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                if(!visited[i][j] && graph[i][j]==1){
                    visited[i][j]=true;
                    res++; 
                    dfs(visited, graph, i, j);
                }
            }
        }
        System.out.println(res);
     }
}

广度优先遍历需要定义一个队列，注意每把一个Pair加入队列时，都要立马让visited标记为true，避免重复遍历

java 复制代码

import java.util.*;

public class Main{
    public static int[][] dir = {{0,-1}, {0,1}, {-1,0}, {1,0}};

    public static class Pair{ //定义一个Pair类
        int first;
        int second;

        public Pair(int x, int y){
            this.first = x;
            this.second = y;
        }
    }

    public static void bfs(boolean[][] visited, int[][] graph, int x, int y){
        Queue<Pair> que = new LinkedList<>();
        que.offer(new Pair(x,y));
        visited[x][y] = true;//入队就直接标记为访问过
        while(!que.isEmpty()){
            int curX = que.peek().first;
            int curY = que.poll().second; //出队
            for(int i=0;i<4;i++){
                int nextX = curX+dir[i][0];
                int nextY = curY+dir[i][1];
                if(nextX<0 || nextY<0 || nextX>=graph.length || nextY>=graph[0].length) continue; //超出图的部分直接跳出循环
                if(!visited[nextX][nextY] && graph[nextX][nextY]==1){
                    que.offer(new Pair(nextX, nextY));
                    visited[nextX][nextY] = true;
                }
            }
        }
    }

    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        int[][] graph = new int[n][m];
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                graph[i][j] = sc.nextInt();
            }
        }
        boolean[][] visited = new boolean[n][m];
        int res = 0;
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                if(!visited[i][j] && graph[i][j]==1){
                    res++; 
                    bfs(visited, graph, i, j);
                }
            }
        }
        System.out.println(res);
     }
}