问题描述:
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例1:
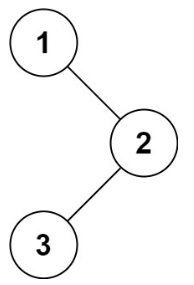
**输入:**root = [1,null,2,3]
输出:[1,3,2]
示例2:
**输入:**root = []
输出:[]
示例3:
**输入:**root = [1]
输出:[1]
解决方法:
方法一:递归法
算法思路:
递归法利用函数调用栈来模拟遍历过程,遵循"左子树-根节点-右子树"的访问顺序,将大问题分解为小问题:遍历整棵树 = 遍历左子树 + 访问根节点 + 遍历右子树。
算法步骤:
-
递归终止条件:如果当前节点为空,直接返回
-
递归左子树:深入遍历当前节点的左子树
-
访问根节点:将当前节点的值加入结果列表
-
递归右子树:深入遍历当前节点的右子树
代码实现:
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
result = []
# 调用辅助递归函数,从根节点开始遍历
self.inorder(root,result)
return result
def inorder(self,node,result):
# 递归终止条件
if node is None:
return
# 递归遍历左子树 深入当前节点的左子树 直到最左边叶子节点
self.inorder(node.left,result)
# 访问当前节点-根节点 在左子树遍历完成后,将当前节点的值加入结果列表
result.append(node.val)
# 递归遍历右子树 在访问完当前节点后,深入右子树继续遍历
self.inorder(node.right,result)
# self 是 Python 类方法的第一个参数,代表实例本身
# 在类的方法中调用其他方法必须使用 self.方法名()
# 这是 Python 面向对象编程的语法要求,不是算法本身的需要复杂度分析:
- 时间复杂度:O(n),每个节点恰好被访问一次
- 空间复杂度:O(h),h为二叉树的高度
方法二:迭代法
算法思路:
使用显式的栈来模拟递归的函数调用栈。通过循环和栈操作来实现中序遍历的"左根右"顺序。核心思想是先深入左子树到底部,然后回溯访问节点,再转向右子树。
算法步骤;
-
初始化:创建结果列表、辅助栈,设置当前节点指针
-
循环条件:当前节点不为空或栈不为空时继续
-
左子树处理:将当前节点及其所有左子节点入栈
-
节点访问:弹出栈顶节点,访问该节点
-
右子树处理:转向右子树继续遍历
代码实现:
python
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
# 步骤1:初始化
result = [] # 存储结果
stack = [] # 辅助栈
current = root # 当前节点指针
# 步骤2:循环条件
while current or stack:
# 步骤3:左子树处理 - 遍历到最左边的节点
while current:
stack.append(current)
current = current.left
# 步骤4:节点访问 - 弹出栈顶元素并访问
current = stack.pop()
result.append(current.val)
# 步骤5:右子树处理 - 转向右子树
current = current.right
return result复杂度分析:
- 时间复杂度:O(n),每个节点入栈出栈各一次,共 2n 次操作
- 空间复杂度:O(h),h为二叉树的高度
递归法另一种版本(条件判断)
python
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
# 步骤1:初始化
result = []
stack = []
current = root
# 步骤2:循环条件
while current or stack:
if current:
# 步骤3:节点非空 - 入栈并转向左子树
stack.append(current)
current = current.left
else:
# 步骤4:节点为空 - 回溯访问并转向右子树
current = stack.pop()
result.append(current.val)
current = current.right
return result问题详解:
什么是中序遍历?
中序遍历是二叉树遍历的一种方式,遍历顺序为:
-
左子树:递归遍历左子树
-
根节点:访问当前节点
-
右子树:递归遍历右子树
此外还有前序遍历 (根左右)以及后序遍历(左右根)
总结:
| 方法 | 优点 | 缺点 | 适用场景 |
| 递归法 | 代码简洁,逻辑清晰 | 递归深度大时可能会栈溢出 | 树深度不大 |
| 迭代法 | 避免递归开销,可控性好 | 代码相对复杂 | 深度大的树 |
|---|
核心要点:
- 遍历顺序:牢记"左根右"的中序遍历顺序
- 递归思想:分治思想,将问题分解为子树问题
- 栈的应用:迭代法通过栈模拟递归调用的过程
- 空间优化:两种方法的空间复杂度都与树高相关