算法——二叉树、dfs、bfs、适配器、队列练习

❀保持低旋律节奏->个人主页

文章目录

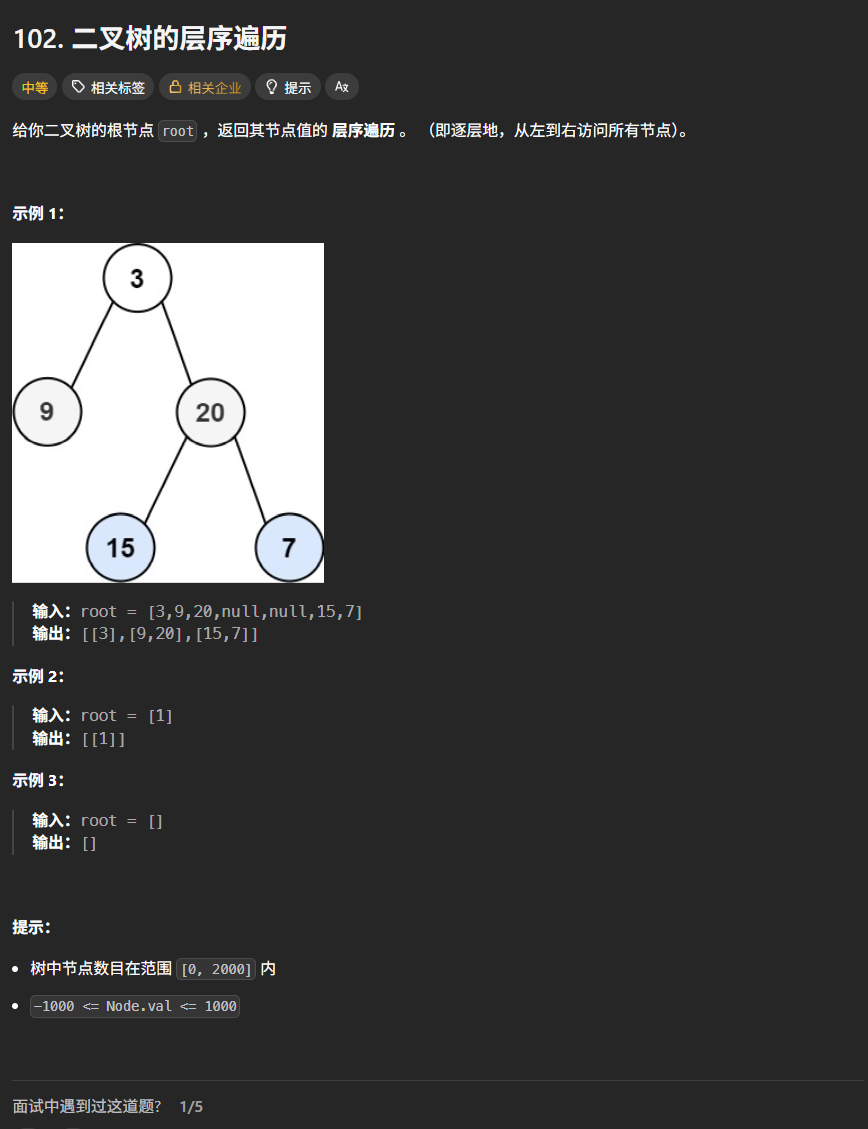
一、二叉树层序遍历

代码实现

cpp 复制代码

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        if(root == nullptr)
        {
            return {};
        }
        //创建vecrot容器，底层使用vector<int>
        vector<vector<int>>ans;
        //创建queue队列，队列底层适配器使用 TreeNode
        queue<TreeNode*>q;
        /*
        //将根节点赋予给q
        //q = root;
        错误写法无法将q赋值给root，只能将root传入到q里面，q里面存储的是root类型
        */
        q.push(root);
        
        while(!q.empty())
        {
            vector<int>vals;

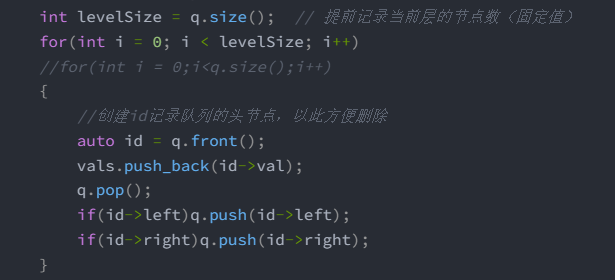
            //隐蔽的错误这里的q.size是动态变化的
            int levelSize = q.size();  // 提前记录当前层的节点数（固定值）
            for(int i = 0; i < levelSize; i++)
            //for(int i = 0;i<q.size();i++)
            {
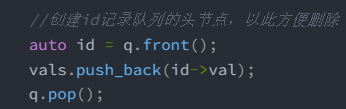
                //创建id记录队列的头节点，以此方便删除
                auto id = q.front();
                vals.push_back(id->val);
                q.pop();
                if(id->left)q.push(id->left);
                if(id->right)q.push(id->right);
            }
            ans.push_back(vals);
        }
        return ans;    
    }
};

题解

核心考察点------bfs思想

一、

这道题的核心考察点在于，队列与节点结合使用。

考察你对队列的掌握，以及底层适配器的掌握。

二、

队列入栈出栈操作->演变为，队列其适配器是节点的入栈和出栈操作

出栈为q.pop这是无疑的，重点在于取队列的元素并放入到vector容器里面

1.先得到头节点的迭代器 auto id = q.front();

2.迭代器解引用 vector再pushback vals.push_back(id->val);

三、

对于for循环的理解。

我们开始先入的root根节点，而后进行两个if判断

目的是为了入根节点的左节点和右节点。

而这里的循环条件是每个节点的大小。

易错题解

一、

这里的size 是用的静态的。

如果for(int i = 0;i<q.size();i++)这里就是动态的会报错！！！

报错的原因在于。

再for循环里q.pop()：删除队首元素 → 让 q.size() 变小；

q.push(子节点)：添加新元素 → 让 q.size() 变大。
问题就在于你可能还没执行完第n次循环呢，pop可能就已经改变了size的大小。导致for循环少遍历了几次

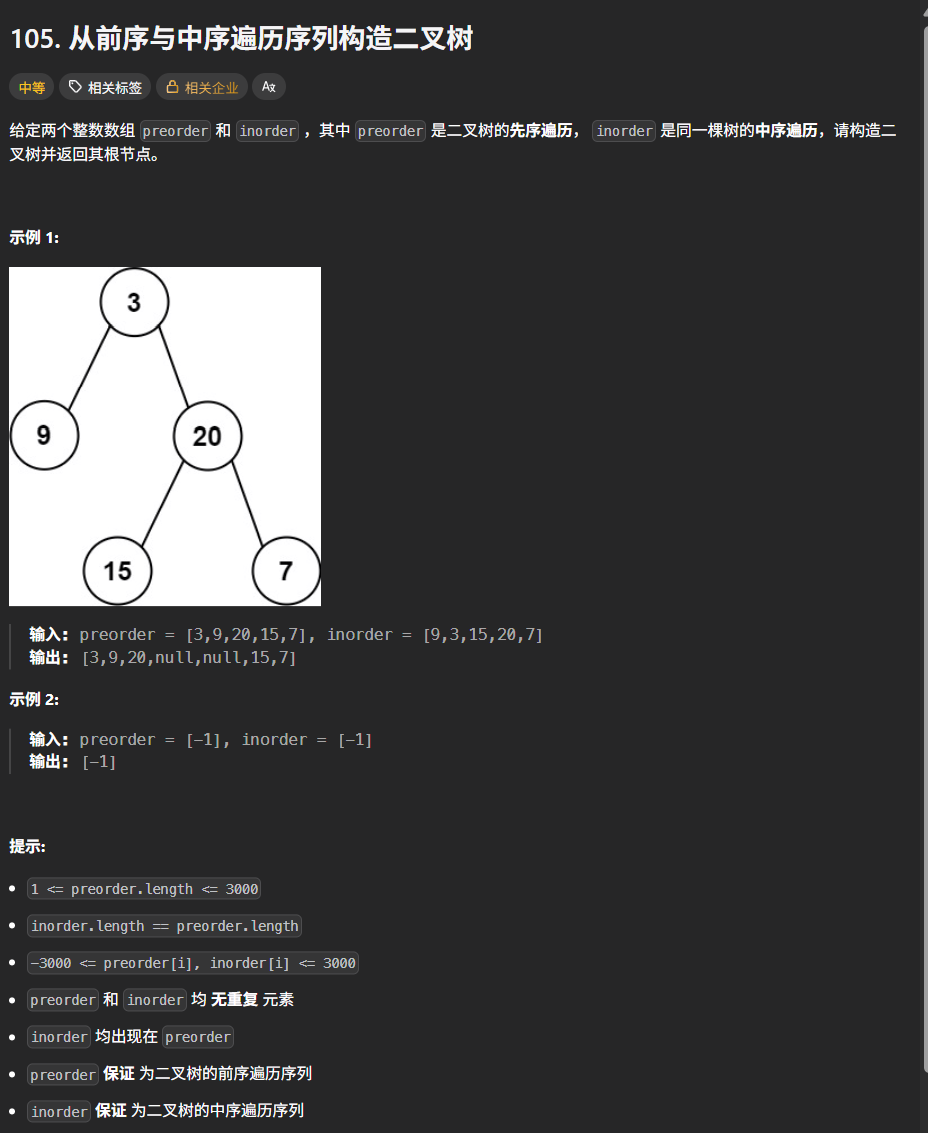
二、从前序与中序遍历序列构造二叉树------二三一起看

从前序与中序遍历序列构造二叉树

代码实现

cpp 复制代码

#include<vector>
#include<algorithm>

class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
    
    //终止条件
    if(preorder.empty()) return nullptr;

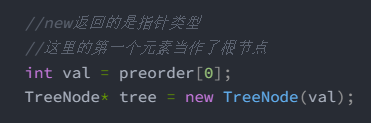
    //new返回的是指针类型
    //这里的第一个元素当作了根节点
    int val = preorder[0];
    TreeNode* tree = new TreeNode(val);
    
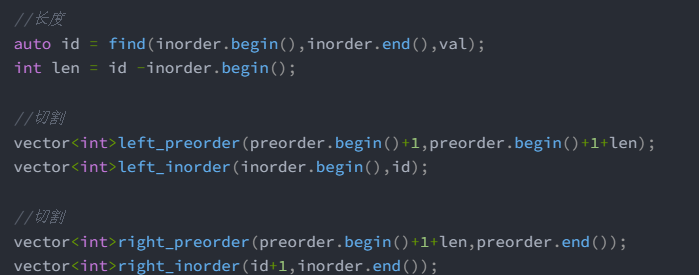
    //长度
    auto id = find(inorder.begin(),inorder.end(),val);
    int len = id -inorder.begin();
    
    //切割
    vector<int>left_preorder(preorder.begin()+1,preorder.begin()+1+len);
    vector<int>left_inorder(inorder.begin(),id);

    //切割
    vector<int>right_preorder(preorder.begin()+1+len,preorder.end());
    vector<int>right_inorder(id+1,inorder.end());

    //递归
    tree->left = buildTree(left_preorder,left_inorder);
    tree->right = buildTree(right_preorder,right_inorder);

    return tree;
    }
};

题解

核心考察点

一、

从构建根节点->转变为从根节点开始递归遍历

根节点的构建可谓是小菜一碟 TreeNode* tree = new TreeNode(val)

根节点的构建和递归联系再一块往往让人想不到

其左右子树分别为

tree->left = buildTree(left_preorder,left_inorder);

tree->right = buildTree(right_preorder,right_inorder);

二、

长度也可为是家常便饭了 auto id = find()函数，返回值是一个迭代器

迭代器减去开头的迭代器 = 个数 == 长度

难得地方在于

如何递归调用开头

找到根节点通过调左序列得左半部分
找到根节点通过调中序列得左半部分

找到根节点通过调左序列得右半部分
找到根节点通过调中序列得右半部分 对于这部分得理解是难点！！！

易错题解

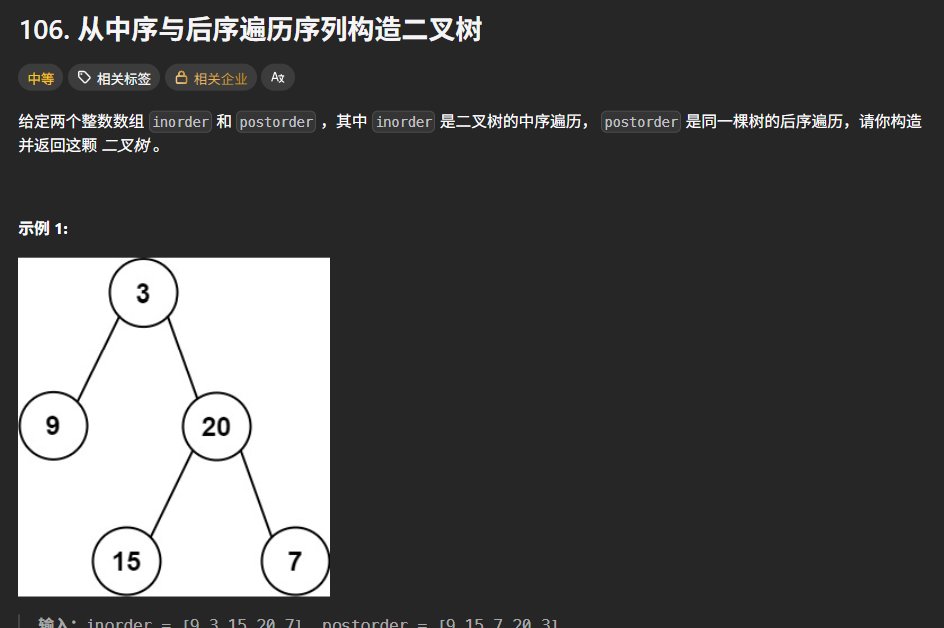
三、从中序与后续遍历序列构造二叉树------二三一起看

从中序与后续遍历序列构造二叉树

代码实现

cpp 复制代码

#include<vector>
#include<algorithm>


class Solution {
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
     
     //终止条件
     if(inorder.empty()) return nullptr;

    //构建根节点，但凡涉及到二叉树的一定会涉及到节点
    //后面用于连接，从而形成二叉树
    //root->left
    //root->right

    int final = postorder.size()-1;
    TreeNode* root = new TreeNode(postorder[final]);
    
     //postorder找根，inorder中截取
     auto id = find(inorder.begin(),inorder.end(),postorder[final]);
     int len = id-inorder.begin();

     //截取
     vector<int> right_postorder(postorder.begin() + len,postorder.end()-1);
     vector<int>right_inorder(id+1,inorder.end());

     //截取
     vector<int> left_postorder(postorder.begin(),postorder.begin() + len);
     vector<int> left_inorder(inorder.begin(),id);

     root->right = buildTree(right_inorder,right_postorder);
     root->left = buildTree(left_inorder,left_postorder);
     return root;


    }
};

题解

核心考察点

易错题解

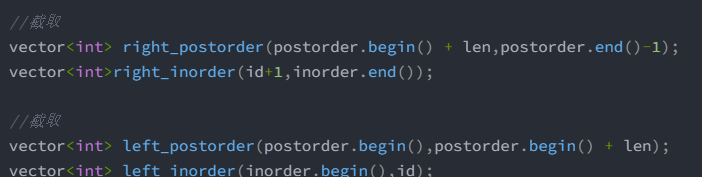
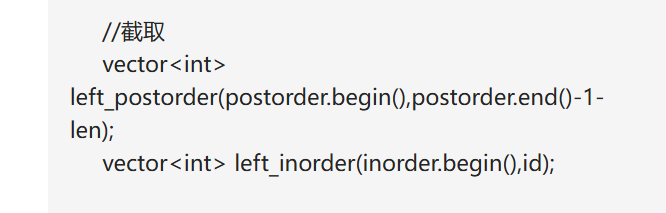
截取尽量不要从后往前截取。尽量从前往后截取。这样不容易出错

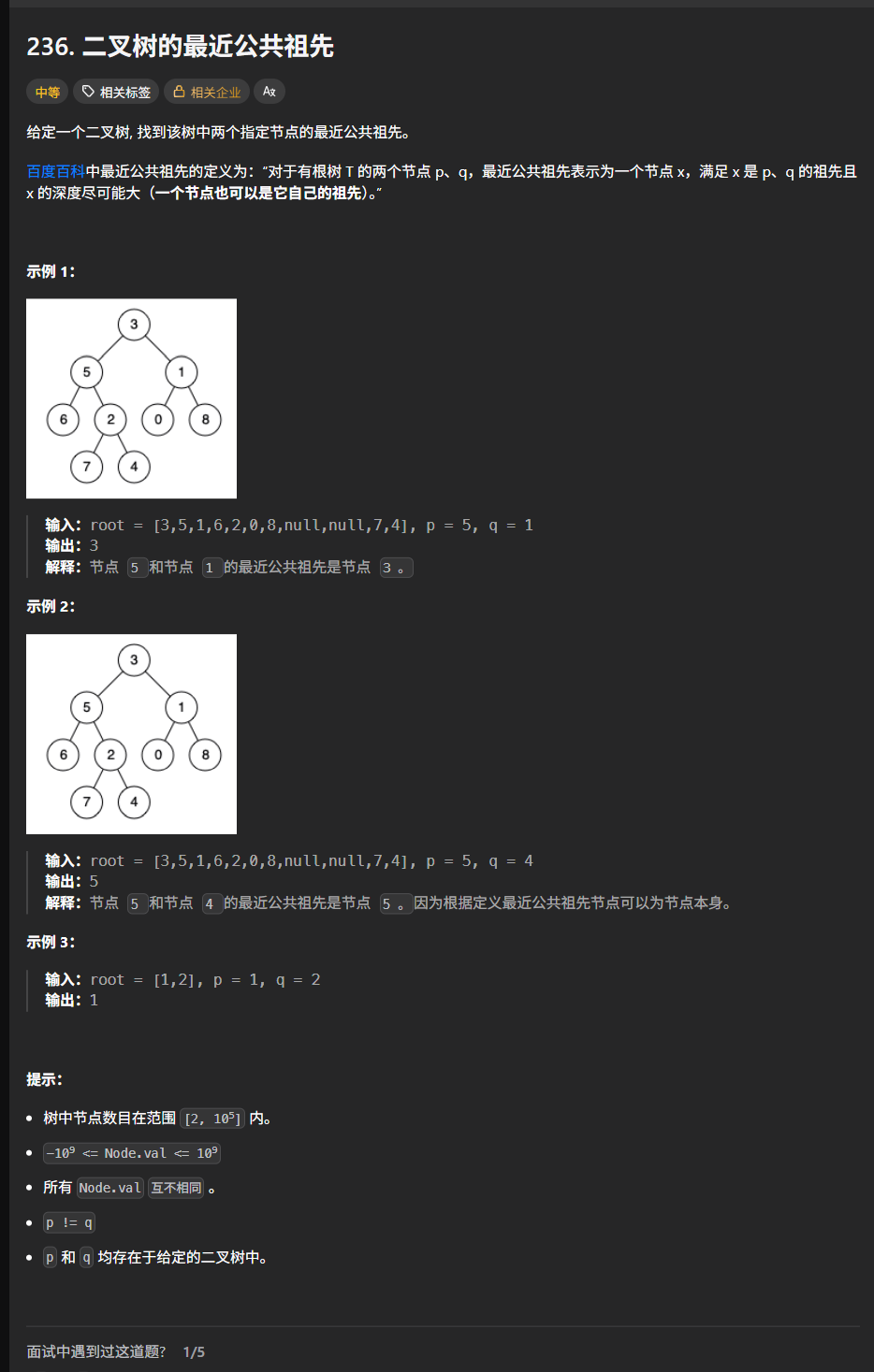
四、二叉树的最近公共祖先------三四一起分析------抽象题

二叉树的最近公共祖先

代码实现

cpp 复制代码

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        
        //3.补充------写终止条件
        //如果为空那就结束
        //如果不是空那就root = p root = q继续遍历
        if (!root||root == p||root ==q)return root;
        //void dis(TreeNode* root, TreeNode* p, TreeNode* q)

        //1.递归遍历
       //进入下一个循环
        /*lowestCommonAncestor(root->left, p, q);
        lowestCommonAncestor(root->right, p, q);*/

        //付给我的左子树或右子树
        //2.不能付给root，root是根节点遍历的起点。
        //创建新节点，然后接受
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);

        //4.补充最终条件
        // 情况1：左右都找到 → 当前 root 就是最近公共祖先
        if (left && right) return root;

        // 情况2：只找到一个 → 把那个往上返回
        return left ? left : right;

    }
};

题解

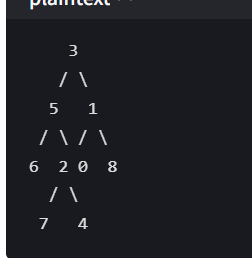
假如p=5 q=4

核心考察点

一、

递归调用最开始从底层开始分析，就拿上图来说。第一个调用为 (7,5,4)然后是（4，5，4）

二、

当你仅仅找到一个节点时侯return 为什么不会停止递归，你可以理解为在这个题目里面必须找到2个节点才会终止。

第一个 return root 是 "传递位置信息" ，触发后会继续向上传递，直到遇到能 "宣布最终答案" 的节点。

你也可以理解为第二个 return root 是 "宣布最终答案" ，一旦触发，递归会直接结束；

三、
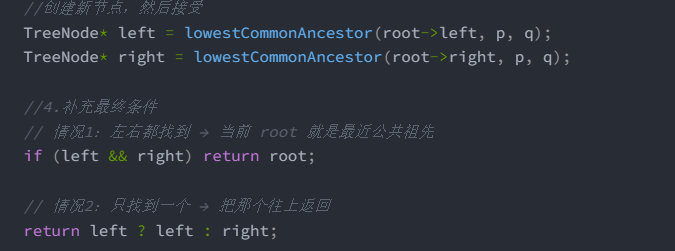
递归得本质，向下递归，向上返回！！！。所以最后一行是返回的是上一层递归的left和right而不是自己下一层的。！！！

易错题解

五、二叉搜索树与双向链表------三四一起分析------抽象题

二叉搜索树与双向链表

代码实现

cpp 复制代码

class Solution {
public:
//定义pre前序，前序用于向前遍历
//头节点用于记录第一个节点
    TreeNode* pre = nullptr;
	TreeNode* head = nullptr;
    TreeNode* Convert(TreeNode* pRootOfTree) {
     if(pRootOfTree==nullptr) return nullptr;
	 //开始遍历直到最后
	 Convert(pRootOfTree->left);
    if(pre == nullptr)
	{
		head = pRootOfTree;
	}
	//保证pre是pRootOfTree的前一个节点
	else 
	{
		//把pre赋值给 pRootOfTree的左指针
        pRootOfTree->left=pre;
		pre->right = pRootOfTree;
	}
	//处理第一个节点
	pre = pRootOfTree; 
	//开始遍历中序右节点
	Convert(pRootOfTree->right);
	return head;
    }
};

题解

核心考察点

抽象点一、

对于递归的理解这里非常非常抽象！！

在这道题里面递归是先往前递归一条路走到黑。然后再从中序开始往后递归。

往前递归完之后，找到第一个节点pRootOfTree开始往后递归，此时的pRootOfTree仍然是中间那个节点！！

抽象点二、

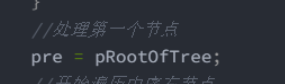
这一行代码他只会再头节点的时候出发，虽然每条递归里面都有这行代码。但是它的作用旨在第一行代码

下面解释

因为递归的底层是从最低端开始的。而我们往前递归，最开始就是从头部开始的。因此pre这条指令旨在最开始的时候起到了作用。这里你也不需要担心，pre=pRootOfTree这条指令会不会破坏了节点之间的联系。

完全不会！！因为代码是从最低端开始的。但是代码它执行过程是最上端开始往下面递归的。

这是很抽象的。