目录
[1.1 定义与性质](#1.1 定义与性质)
[1.2 核心特性:中序遍历有序性](#1.2 核心特性:中序遍历有序性)
[2.1 时间复杂度分析](#2.1 时间复杂度分析)
[2.2 与二分查找的对比](#2.2 与二分查找的对比)
[三、二叉搜索树的核心操作实现(Key 型)](#三、二叉搜索树的核心操作实现(Key 型))
[3.1 节点结构设计](#3.1 节点结构设计)
[3.2 二叉搜索树类框架](#3.2 二叉搜索树类框架)
[3.3 插入操作实现](#3.3 插入操作实现)
[3.4 查找操作实现](#3.4 查找操作实现)
[3.5 删除操作实现](#3.5 删除操作实现)
[3.5.1 删除场景分类](#3.5.1 删除场景分类)
[3.5.2 删除逻辑实现](#3.5.2 删除逻辑实现)
[3.6 测试代码与结果](#3.6 测试代码与结果)
[四、Key/Value 型二叉搜索树实现](#四、Key/Value 型二叉搜索树实现)
[4.1 节点结构设计](#4.1 节点结构设计)
[4.2 二叉搜索树类实现](#4.2 二叉搜索树类实现)
[4.3 核心操作实现](#4.3 核心操作实现)
[4.3.1 插入操作](#4.3.1 插入操作)
[4.3.2 查找操作](#4.3.2 查找操作)
[4.4 测试代码与结果](#4.4 测试代码与结果)
[4.4.1 中英字典案例](#4.4.1 中英字典案例)
[4.4.2 单词计数案例](#4.4.2 单词计数案例)
[5.1 关于Key 型场景的存在性验证](#5.1 关于Key 型场景的存在性验证)
[5.1.1 小区车库车牌验证](#5.1.1 小区车库车牌验证)
[5.1.2 单词拼写检查](#5.1.2 单词拼写检查)
[5.2 Key/Value 型场景:映射与统计](#5.2 Key/Value 型场景:映射与统计)
[5.2.1 简单中英互译字典](#5.2.1 简单中英互译字典)
[5.2.2 停车场计时收费](#5.2.2 停车场计时收费)
[5.2.3 文章单词计数](#5.2.3 文章单词计数)
[6.1 核心缺陷:退化风险](#6.1 核心缺陷:退化风险)
[6.2 优化方向:平衡二叉树](#6.2 优化方向:平衡二叉树)
[6.3 STL 中的二叉搜索树应用](#6.3 STL 中的二叉搜索树应用)
前言
在数据结构与算法的学习中,二叉搜索树 (Binary Search Tree,简称 BST)是连接线性结构与复杂树形结构的关键节点。它不仅是理解后续平衡二叉树(AVL 树、红黑树)的基础,更在实际开发中有着广泛的应用 ------ 从简单的单词拼写检查到复杂的键值对存储,二叉搜索树都以高效的增删查改特性占据重要地位。
本文将基于 C++ 语言,从概念定义、性能分析、核心操作实现、多场景适配到实际应用案例,全方位拆解二叉搜索树。下面就让我们正式开始吧!
一、二叉搜索树的核心概念
1.1 定义与性质
二叉搜索树又称二叉排序树,它要么是一棵空树,要么是满足以下递归性质的二叉树:
- 若左子树不为空,则左子树上所有节点的值小于等于根节点的值(相等值的处理可灵活定义);
- 若右子树不为空,则右子树上所有节点的值大于等于根节点的值;
- 左右子树也必须分别是二叉搜索树。
这里需要特别说明一下:二叉搜索树对相等值的支持是灵活的 ------ 部分场景(比如我们后面会学习的 set 容器)不允许插入重复值,此时相等值直接返回插入失败;而在允许重复值的场景下(比如multiset等容器),需保持插入逻辑一致(要么均插入左子树,要么均插入右子树,避免破坏排序特性)。
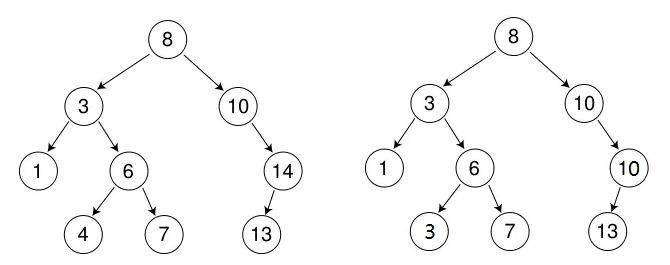
1.2 核心特性:中序遍历有序性
二叉搜索树的核心价值之一在于其中序遍历结果是有序的。无论是升序还是降序,只需调整中序遍历的左右子树访问顺序即可实现。例如:
- 升序遍历:左子树 → 根节点 → 右子树;
- 降序遍历:右子树 → 根节点 → 左子树。
这一特性使得二叉搜索树天然适用于需要排序与查找的场景,也是其区别于普通二叉树的关键标志。
二、二叉搜索树的性能分析
2.1 时间复杂度分析
二叉搜索树的增删查改操作效率直接取决于树的高度,而树的高度由节点插入顺序决定:
-
最优情况:树为完全二叉树(或接近完全二叉树),高度为
(N 为节点总数)。此时所有操作的时间复杂度为
,效率极高;
-
最差情况:树退化为单支树(类似链表),高度为 N。此时所有操作的时间复杂度退化为
,效率是与链表相当的。
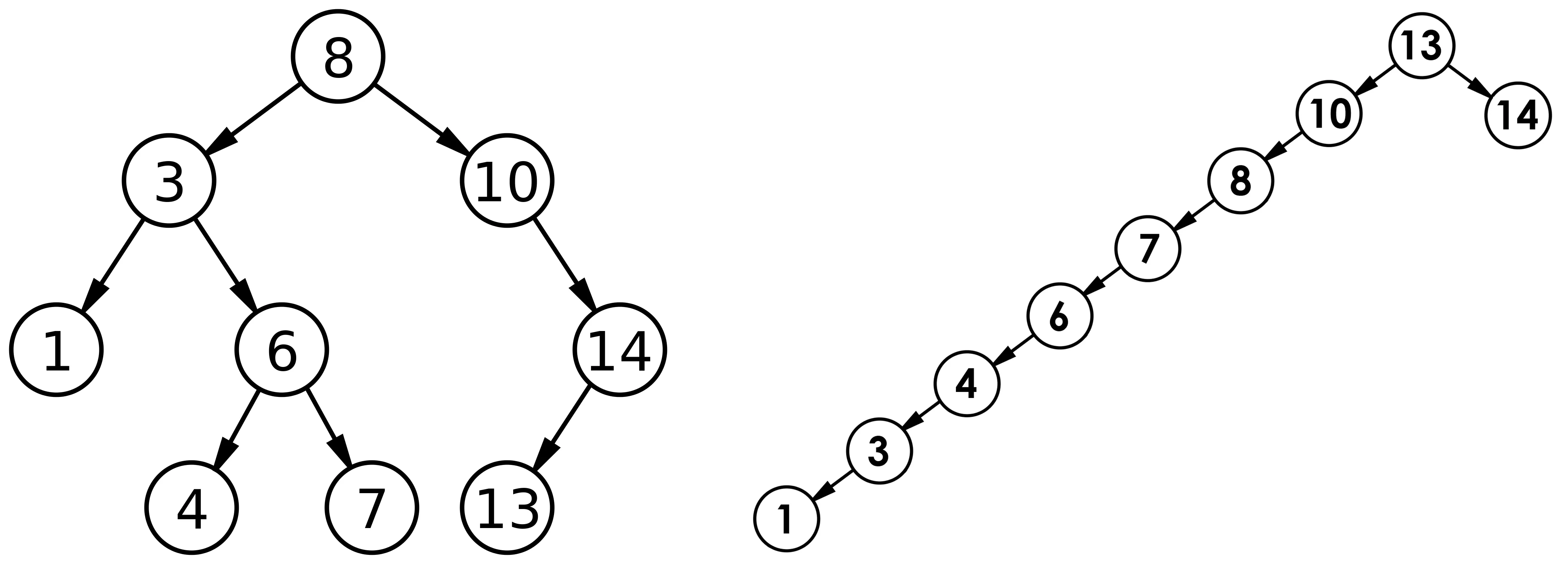
2.2 与二分查找的对比
提到级别的查找效率,很多人会想到二分查找。但二叉搜索树相比二分查找有明显优势,具体对比如下:
| 特性 | 二分查找 | 二叉搜索树 |
|---|---|---|
| 存储结构要求 | 必须是支持随机访问的有序结构(如数组) | 链式存储,无需连续空间 |
| 插入 / 删除效率 | 低(需挪动大量元素,时间复杂度为 O (N)) | 高(仅需调整指针,最优为 O (logN)) |
| 适用场景 | 静态数据(极少插入 / 删除) | 动态数据(频繁增删查改) |
由此可见,二叉搜索树完美弥补了二分查找在动态数据处理上的缺陷,这也是其在实际开发中被广泛应用的核心原因。而后续的平衡二叉树(AVL 树、红黑树),本质上就是通过维持树的平衡来避免单支树退化,确保操作效率稳定在级别。
三、二叉搜索树的核心操作实现(Key 型)
接下来我们来实现一下仅存储**关键码(Key)**的二叉搜索树,支持插入、查找、删除、中序遍历等核心操作:
3.1 节点结构设计
二叉搜索树的节点采用链式存储,每个节点包含关键码、左子树指针和右子树指针:
cpp
template<class K>
struct BSTNode {
K _key; // 关键码
BSTNode<K>* _left; // 左子树指针
BSTNode<K>* _right; // 右子树指针
// 构造函数:初始化关键码,左右指针置空
BSTNode(const K& key)
: _key(key)
, _left(nullptr)
, _right(nullptr) {}
};3.2 二叉搜索树类框架
树类包含根节点指针,并提供插入、查找、删除、中序遍历等接口,私有成员包含辅助函数:
cpp
template<class K>
class BSTree {
typedef BSTNode<K> Node; // 简化节点类型名
public:
// 构造函数:根节点初始化为空
BSTree() : _root(nullptr) {}
// 析构函数:释放所有节点
~BSTree() {
Destroy(_root);
_root = nullptr;
}
// 插入操作
bool Insert(const K& key);
// 查找操作
bool Find(const K& key);
// 删除操作
bool Erase(const K& key);
// 中序遍历(升序)
void InOrder() {
_InOrder(_root);
cout << endl;
}
private:
// 中序遍历辅助函数(递归实现)
void _InOrder(Node* root) {
if (root == nullptr)
return;
_InOrder(root->_left); // 访问左子树
cout << root->_key << " "; // 访问根节点
_InOrder(root->_right); // 访问右子树
}
// 销毁树辅助函数(后序遍历)
void Destroy(Node* root) {
if (root == nullptr)
return;
Destroy(root->_left); // 销毁左子树
Destroy(root->_right); // 销毁右子树
delete root; // 释放当前节点
}
private:
Node* _root; // 根节点指针
};3.3 插入操作实现
插入操作的核心是遵循二叉搜索树的性质,找到合适的空位置插入新节点:
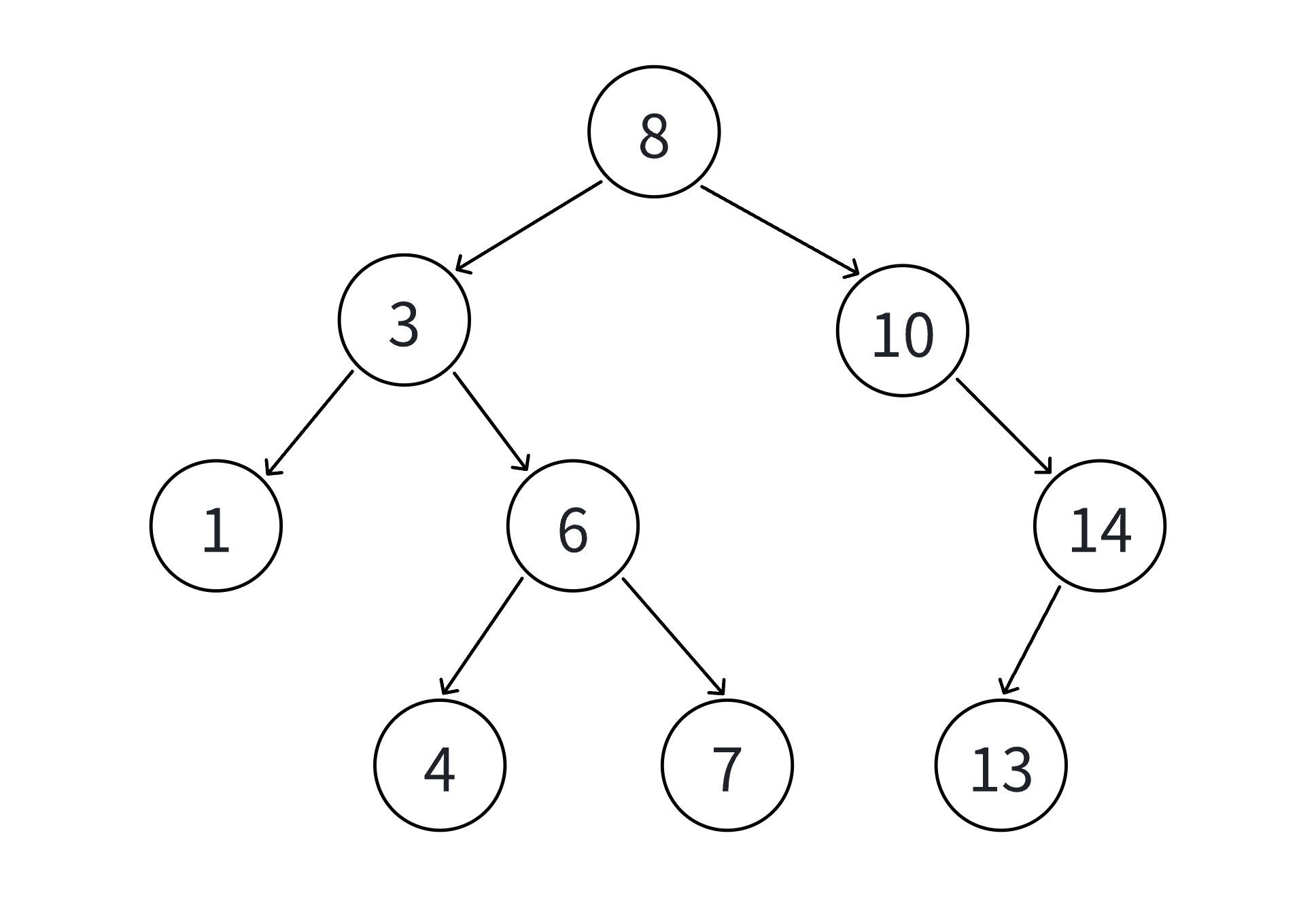
cpp
template<class K>
bool BSTree<K>::Insert(const K& key) {
// 情况1:树为空,直接创建根节点
if (_root == nullptr) {
_root = new Node(key);
return true;
}
// 情况2:树非空,查找插入位置
Node* parent = nullptr; // 记录当前节点的父节点
Node* cur = _root; // 遍历指针,从根节点开始
while (cur) {
if (cur->_key < key) {
// 插入值大于当前节点,向右子树查找
parent = cur;
cur = cur->_right;
} else if (cur->_key > key) {
// 插入值小于当前节点,向左子树查找
parent = cur;
cur = cur->_left;
} else {
// 找到相等值,不支持重复插入,返回失败
return false;
}
}
// 找到空位置,创建新节点
cur = new Node(key);
// 根据父节点与新节点的大小关系,确定新节点是左孩子还是右孩子
if (parent->_key < key) {
parent->_right = cur;
} else {
parent->_left = cur;
}
return true;
}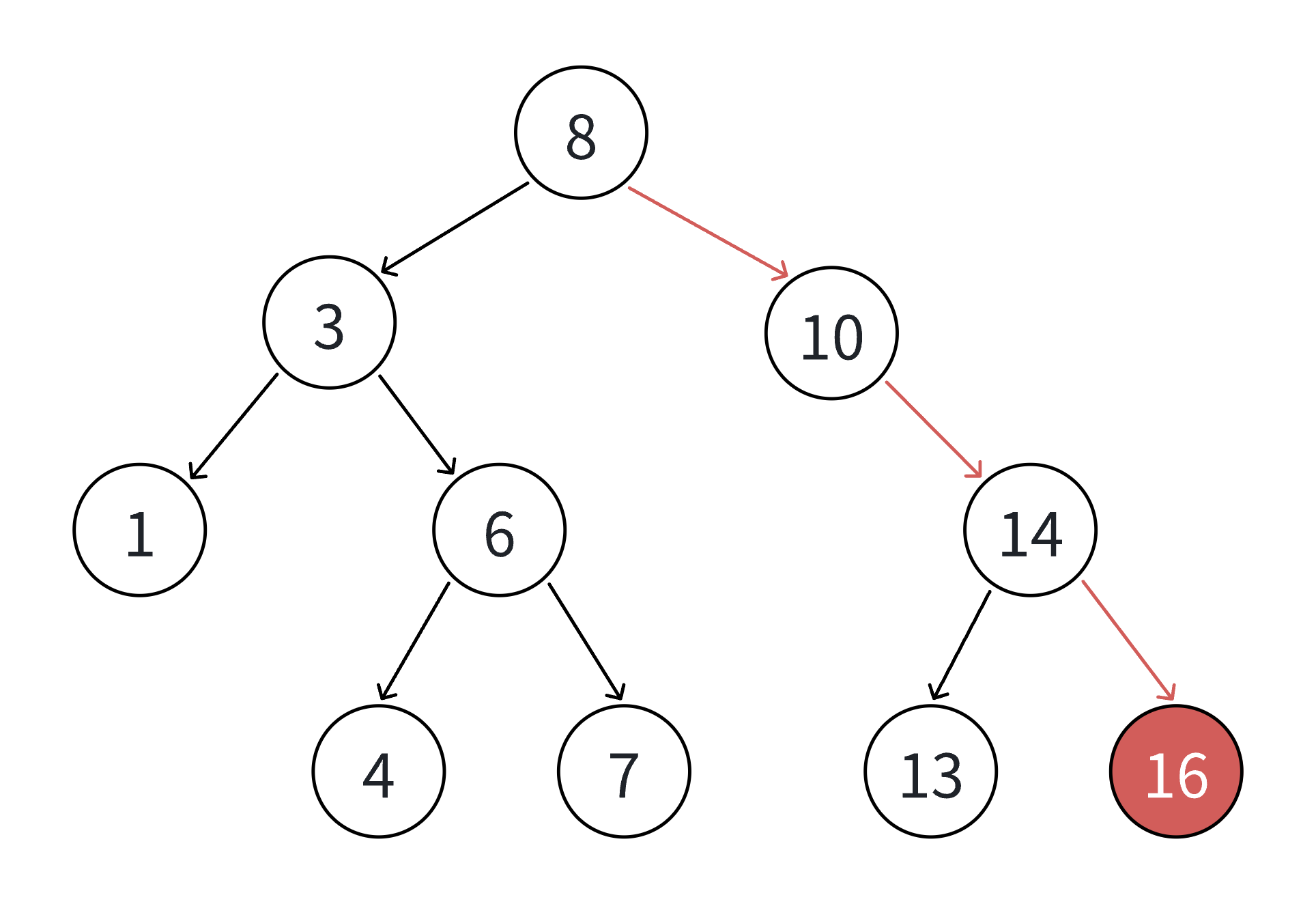
说明:
- 插入前需要先判断树是否为空,如果为空则直接创建根节点;
- 非空树需通过循环遍历找到插入位置,遍历过程中需记录父节点(否则无法挂载新节点);
- 若遇到相等值,直接返回false(不支持重复插入);
- 新节点创建后,根据父节点的关键码判断是挂载为左孩子还是右孩子。
3.4 查找操作实现
查找操作基于二叉搜索树的性质,从根节点开始比较,逐步缩小查找范围:
cpp
template<class K>
bool BSTree<K>::Find(const K& key) {
Node* cur = _root; // 遍历指针,从根节点开始
while (cur) {
if (cur->_key < key) {
// 查找值大于当前节点,向右子树查找
cur = cur->_right;
} else if (cur->_key > key) {
// 查找值小于当前节点,向左子树查找
cur = cur->_left;
} else {
// 找到目标值,返回true
return true;
}
}
// 遍历至空节点仍未找到,返回false
return false;
}
说明:
- 查找过程无需记录父节点,仅需根据关键码大小关系调整遍历方向;
- 查找次数最多为树的高度,最优情况
,最差情况为
;
- 若支持重复插入(如 multiset 场景),查找需返回中序遍历的第一个目标值(通常是左子树最深的目标节点),需在代码中额外处理。
3.5 删除操作实现
删除操作是二叉搜索树中最复杂的操作,需根据待删除节点的子树情况分四种场景处理,核心原则是删除节点后仍保持二叉搜索树的性质。
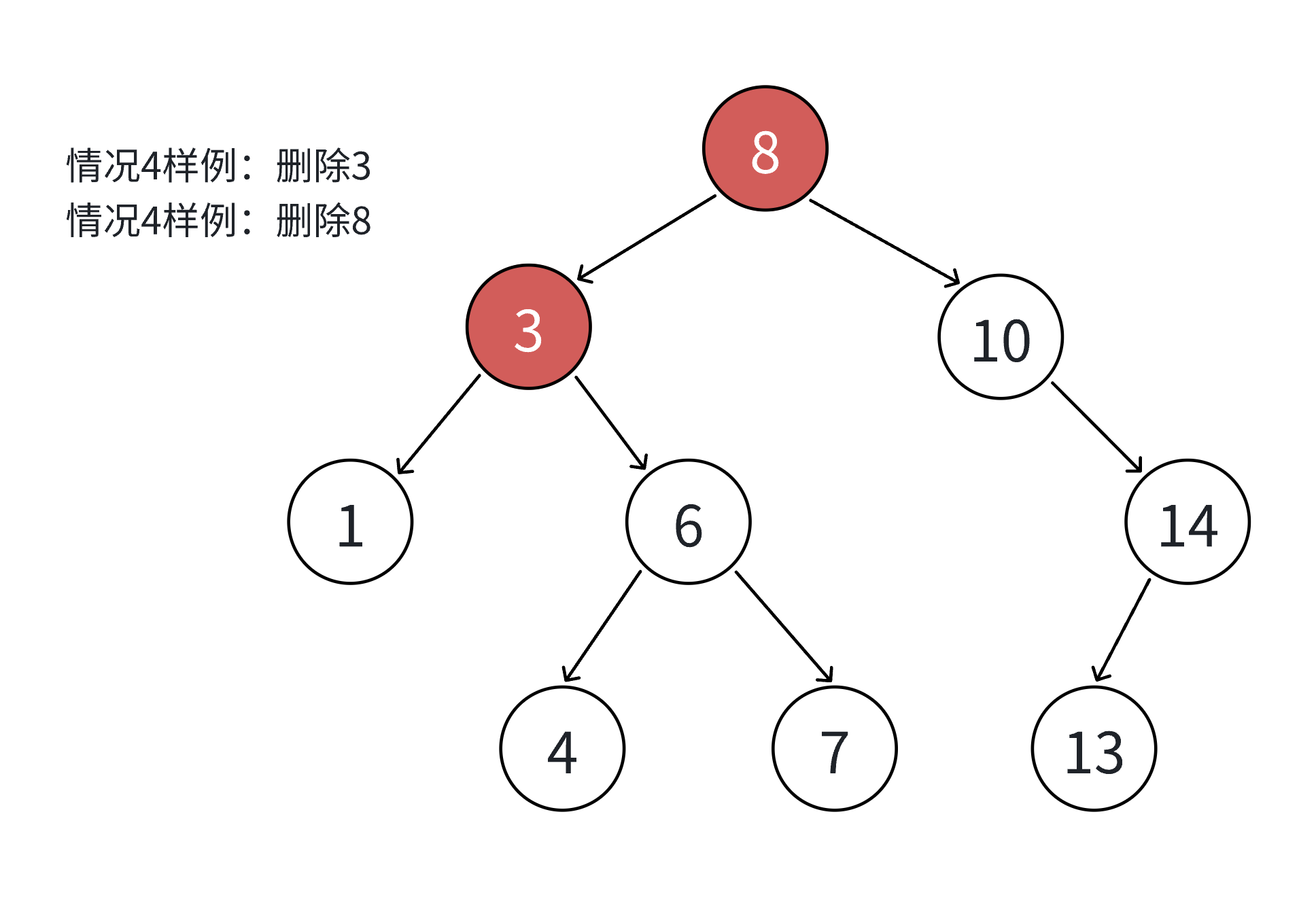
3.5.1 删除场景分类
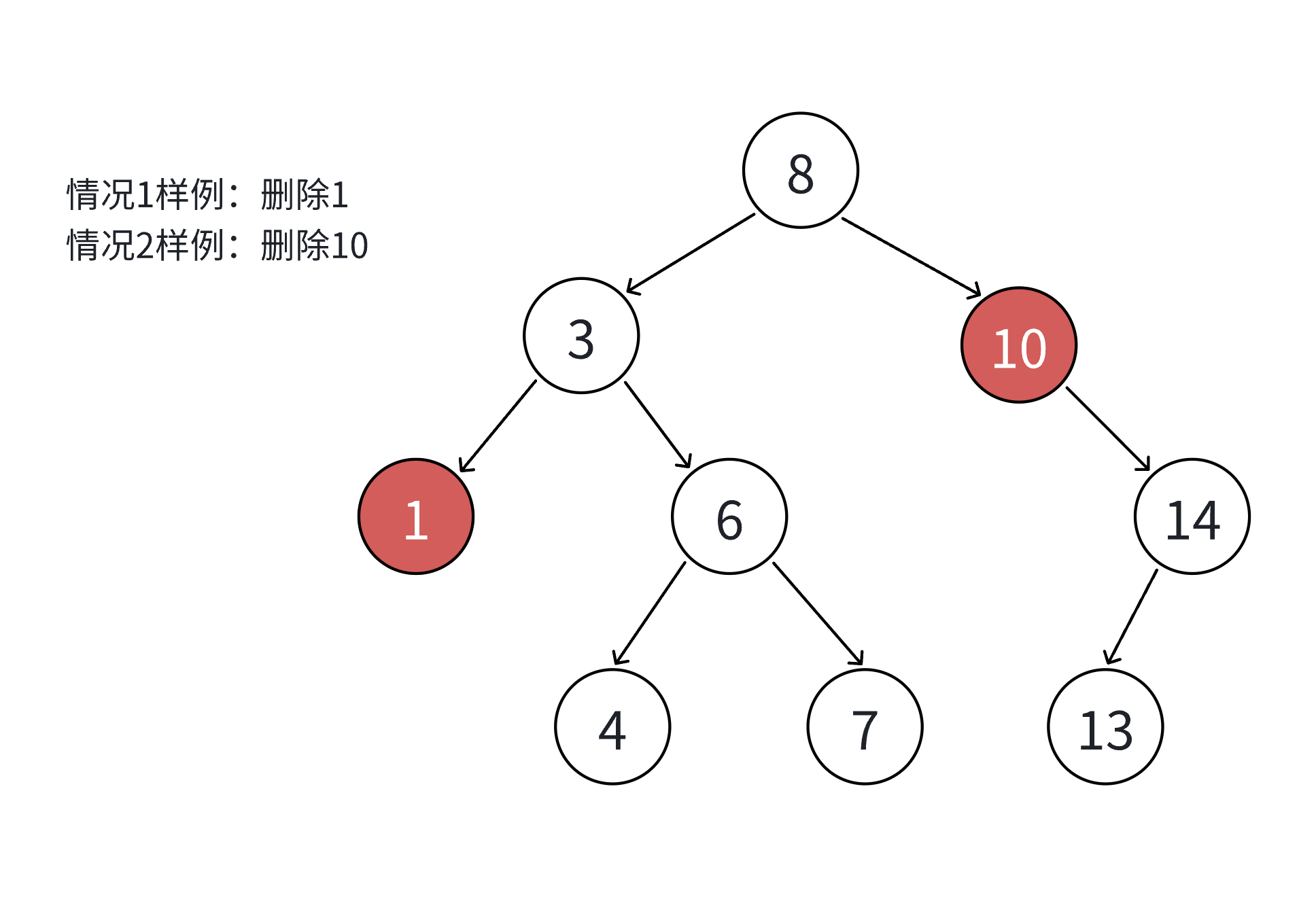
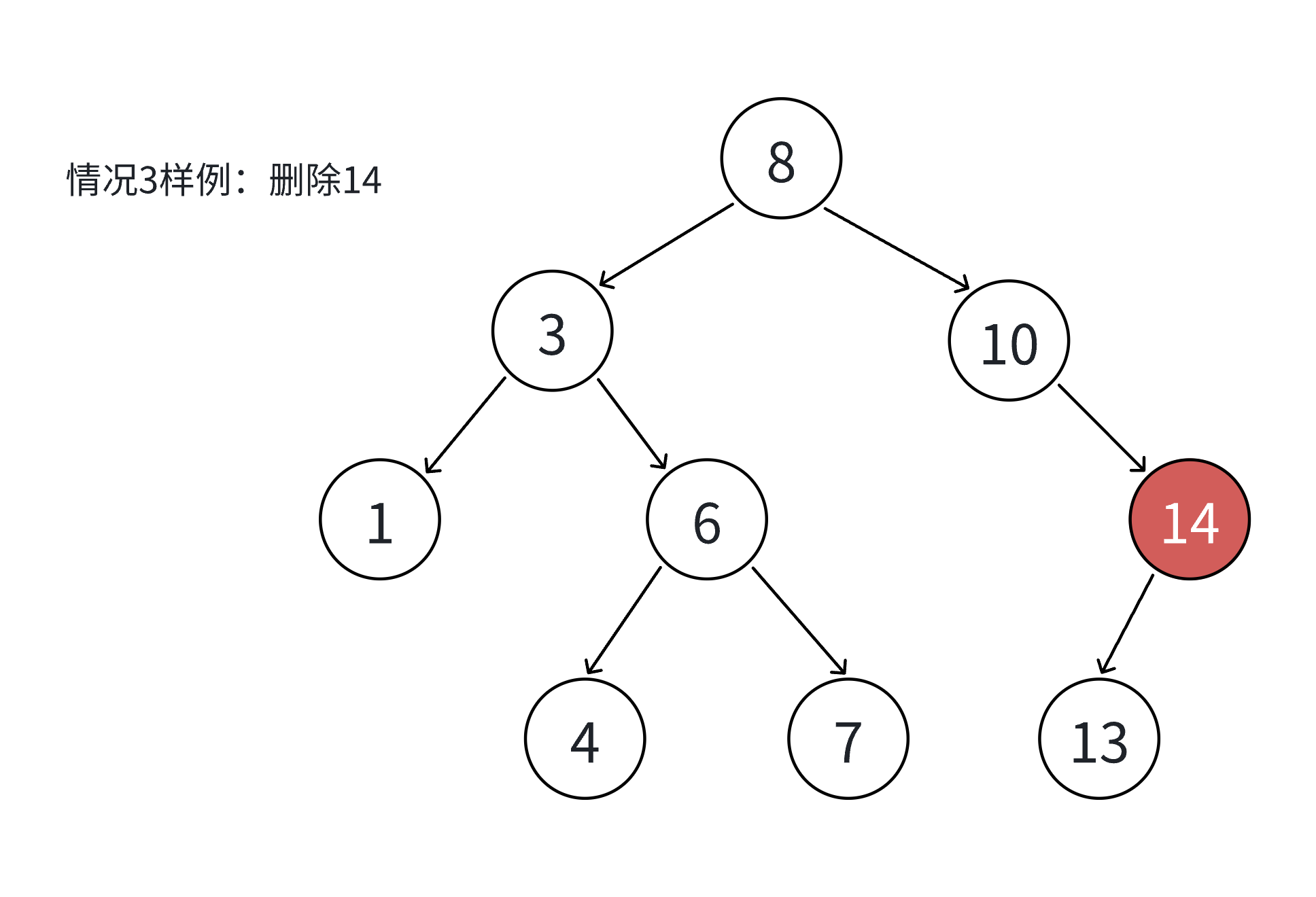
假设待删除节点为 N,共分为四种情况:
- N 的左右子树均为空(叶子节点);
- N 的左子树为空,右子树不为空;
- N 的右子树为空,左子树不为空;
- N 的左右子树均不为空。
其中情况 1 可视为情况 2 或 3 的特例(子树为空),因此实际处理时可合并为三类场景。
3.5.2 删除逻辑实现
cpp
template<class K>
bool BSTree<K>::Erase(const K& key) {
Node* parent = nullptr; // 待删除节点的父节点
Node* cur = _root; // 待删除节点
// 第一步:查找待删除节点
while (cur) {
if (cur->_key < key) {
parent = cur;
cur = cur->_right;
} else if (cur->_key > key) {
parent = cur;
cur = cur->_left;
} else {
// 找到待删除节点,进入删除逻辑
break;
}
}
// 未找到待删除节点,返回false
if (cur == nullptr) {
return false;
}
// 第二步:分场景处理删除
// 场景1:左子树为空(包含左右均为空的情况)
if (cur->_left == nullptr) {
// 若待删除节点是根节点,直接让根节点指向右子树
if (parent == nullptr) {
_root = cur->_right;
} else {
// 判断待删除节点是父节点的左孩子还是右孩子
if (parent->_left == cur) {
parent->_left = cur->_right;
} else {
parent->_right = cur->_right;
}
}
delete cur; // 释放节点内存
return true;
}
// 场景2:右子树为空
else if (cur->_right == nullptr) {
// 若待删除节点是根节点,直接让根节点指向左子树
if (parent == nullptr) {
_root = cur->_left;
} else {
// 判断待删除节点是父节点的左孩子还是右孩子
if (parent->_left == cur) {
parent->_left = cur->_left;
} else {
parent->_right = cur->_left;
}
}
delete cur; // 释放节点内存
return true;
}
// 场景3:左右子树均不为空(替换法删除)
else {
// 方案:找到右子树的最小节点(最左节点)作为替换节点
Node* rightMinP = cur; // 替换节点的父节点
Node* rightMin = cur->_right; // 替换节点(右子树最左节点)
// 找到右子树的最左节点(最小节点)
while (rightMin->_left) {
rightMinP = rightMin;
rightMin = rightMin->_left;
}
// 用替换节点的关键码覆盖待删除节点的关键码
cur->_key = rightMin->_key;
// 删除替换节点(替换节点的左子树为空,属于场景1)
if (rightMinP->_left == rightMin) {
rightMinP->_left = rightMin->_right;
} else {
// 特殊情况:右子树的根节点就是最小节点(无左子树)
rightMinP->_right = rightMin->_right;
}
delete rightMin; // 释放替换节点内存
return true;
}
}说明:
- 场景 1 和场景 2 的处理逻辑类似:直接让父节点指向待删除节点的非空子树,然后释放节点内存;
- 场景 3(左右子树均不为空)是核心难点:无法直接删除节点(会导致子树丢失),因此采用**"替换法"**------ 选择待删除节点右子树的最小节点(或左子树的最大节点)作为替换节点,替换后删除替换节点(替换节点必然是场景 1 或场景 2,可直接删除);
- 替换节点的选择依据:右子树最小节点(最左节点)的关键码是待删除节点右子树中最小的,替换后仍满足 "左子树所有节点≤根节点≤右子树所有节点" 的性质;同理,左子树最大节点(最右节点)也可作为替换节点。
3.6 测试代码与结果
cpp
#include <iostream>
using namespace std;
// 此处粘贴上述BSTNode结构和BSTree类的完整代码
int main() {
BSTree<int> bst;
int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};
// 插入测试
for (auto key : a) {
bst.Insert(key);
}
cout << "中序遍历(升序):";
bst.InOrder(); // 输出:1 3 4 6 7 8 10 13 14
// 查找测试
int findKey1 = 6, findKey2 = 9;
cout << "查找" << findKey1 << ":" << (bst.Find(findKey1) ? "存在" : "不存在") << endl; // 存在
cout << "查找" << findKey2 << ":" << (bst.Find(findKey2) ? "存在" : "不存在") << endl; // 不存在
// 删除测试(叶子节点)
bst.Erase(1);
cout << "删除1后中序遍历:";
bst.InOrder(); // 输出:3 4 6 7 8 10 13 14
// 删除测试(右子树为空)
bst.Erase(14);
cout << "删除14后中序遍历:";
bst.InOrder(); // 输出:3 4 6 7 8 10 13
// 删除测试(左右子树均不为空)
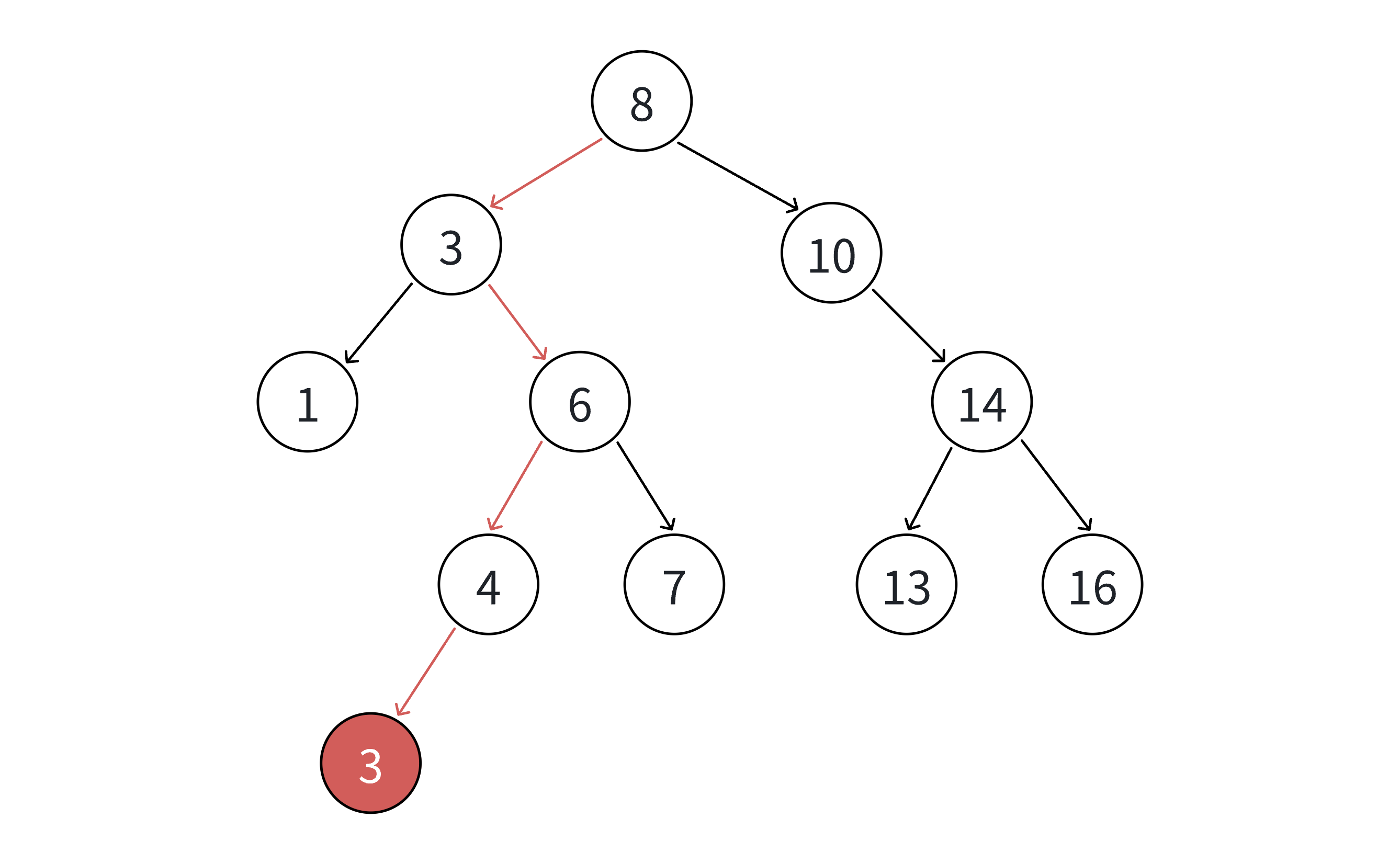
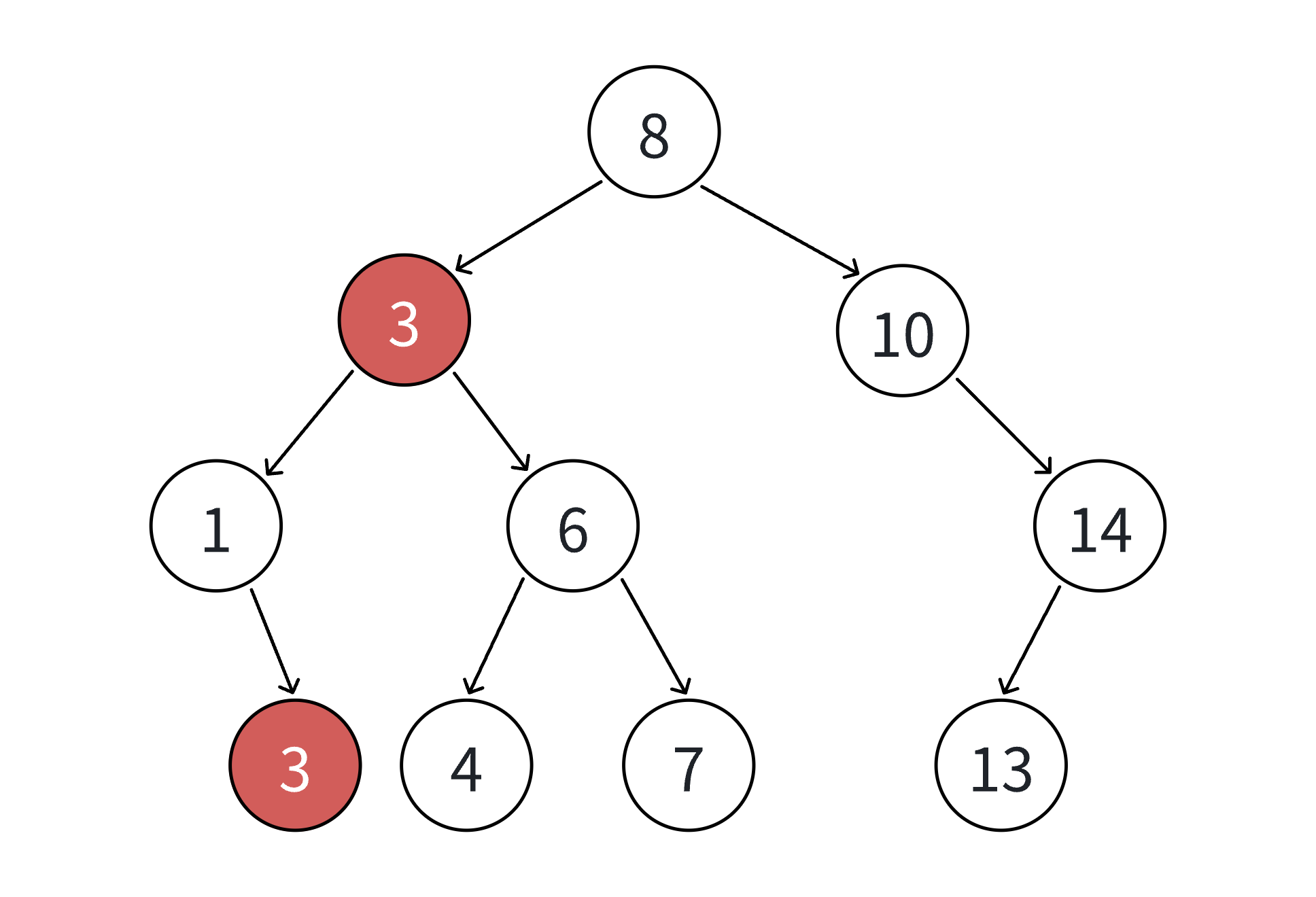
bst.Erase(3);
cout << "删除3后中序遍历:";
bst.InOrder(); // 输出:4 6 7 8 10 13
return 0;
}运行结果:
cpp
中序遍历(升序):1 3 4 6 7 8 10 13 14
查找6:存在
查找9:不存在
删除1后中序遍历:3 4 6 7 8 10 13 14
删除14后中序遍历:3 4 6 7 8 10 13
删除3后中序遍历:4 6 7 8 10 13上面的测试结果验证了插入、查找、删除操作的正确性,且中序遍历始终保持有序。
四、Key/Value 型二叉搜索树实现
在实际开发中,更多场景需要存储**"关键码 - 值"(Key-Value)对**(如字典、缓存)。本节将基于上文中的 Key 型二叉搜索树进行扩展,实现支持 Key-Value 存储的版本。
4.1 节点结构设计
节点需同时存储 Key 和 Value,其他结构与 Key 型一致:
cpp
template<class K, class V>
struct BSTNode {
K _key; // 关键码
V _value; // 对应的值
BSTNode<K, V>* _left; // 左子树指针
BSTNode<K, V>* _right; // 右子树指针
// 构造函数:初始化Key和Value,左右指针置空
BSTNode(const K& key, const V& value)
: _key(key)
, _value(value)
, _left(nullptr)
, _right(nullptr) {}
};4.2 二叉搜索树类实现
相比 Key 型,Key/Value 型的主要变化的是插入、查找接口的参数与返回值,删除逻辑基本一致:
cpp
template<class K, class V>
class BSTree {
typedef BSTNode<K, V> Node;
public:
BSTree() : _root(nullptr) {}
// 拷贝构造函数(深拷贝)
BSTree(const BSTree<K, V>& t) {
_root = Copy(t._root);
}
// 赋值运算符重载(现代写法,利用拷贝构造+交换)
BSTree<K, V>& operator=(BSTree<K, V> t) {
swap(_root, t._root);
return *this;
}
// 析构函数
~BSTree() {
Destroy(_root);
_root = nullptr;
}
// 插入操作:传入Key和Value
bool Insert(const K& key, const V& value);
// 查找操作:返回节点指针(便于修改Value)
Node* Find(const K& key);
// 删除操作:按Key删除
bool Erase(const K& key);
// 中序遍历:输出Key-Value对
void InOrder() {
_InOrder(_root);
cout << endl;
}
private:
// 中序遍历辅助函数
void _InOrder(Node* root) {
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << ":" << root->_value << " ";
_InOrder(root->_right);
}
// 销毁辅助函数
void Destroy(Node* root) {
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
}
// 拷贝辅助函数(深拷贝)
Node* Copy(Node* root) {
if (root == nullptr)
return nullptr;
// 拷贝当前节点
Node* newRoot = new Node(root->_key, root->_value);
// 递归拷贝左右子树
newRoot->_left = Copy(root->_left);
newRoot->_right = Copy(root->_right);
return newRoot;
}
private:
Node* _root;
};4.3 核心操作实现
4.3.1 插入操作
cpp
template<class K, class V>
bool BSTree<K, V>::Insert(const K& key, const V& value) {
if (_root == nullptr) {
_root = new Node(key, value);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur) {
if (cur->_key < key) {
parent = cur;
cur = cur->_right;
} else if (cur->_key > key) {
parent = cur;
cur = cur->_left;
} else {
// Key已存在,不支持重复插入
return false;
}
}
cur = new Node(key, value);
if (parent->_key < key) {
parent->_right = cur;
} else {
parent->_left = cur;
}
return true;
}4.3.2 查找操作
cpp
template<class K, class V>
typename BSTree<K, V>::Node* BSTree<K, V>::Find(const K& key) {
Node* cur = _root;
while (cur) {
if (cur->_key < key) {
cur = cur->_right;
} else if (cur->_key > key) {
cur = cur->_left;
} else {
// 找到Key,返回节点指针(可通过指针修改Value)
return cur;
}
}
return nullptr;
}4.4 测试代码与结果
4.4.1 中英字典案例
cpp
#include <iostream>
#include <string>
using namespace std;
// 此处粘贴Key/Value型BSTNode结构和BSTree类的完整代码
int main() {
// 构建中英字典
BSTree<string, string> dict;
dict.Insert("left", "左边");
dict.Insert("right", "右边");
dict.Insert("insert", "插入");
dict.Insert("string", "字符串");
dict.Insert("search", "查找");
cout << "字典中序遍历(按Key排序):";
dict.InOrder(); // 输出:insert:插入 left:左边 right:右边 search:查找 string:字符串
// 查找并修改Value
string key = "insert";
Node<string, string>* ret = dict.Find(key);
if (ret) {
cout << "修改前 " << key << ":" << ret->_value << endl;
ret->_value = "插入(动词)"; // 修改Value
cout << "修改后 " << key << ":" << ret->_value << endl;
}
// 删除Key
dict.Erase("search");
cout << "删除search后字典:";
dict.InOrder(); // 输出:insert:插入(动词) left:左边 right:右边 string:字符串
return 0;
}4.4.2 单词计数案例
cpp
int main() {
// 统计文章中单词出现次数
string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };
BSTree<string, int> countTree;
for (const auto& str : arr) {
Node<string, int>* ret = countTree.Find(str);
if (ret == nullptr) {
// 单词第一次出现,插入(单词,1)
countTree.Insert(str, 1);
} else {
// 单词已存在,计数+1
ret->_value++;
}
}
cout << "单词出现次数统计:";
countTree.InOrder(); // 输出:苹果:6 香蕉:2 西瓜:3
return 0;
}运行结果:
cpp
字典中序遍历(按Key排序):insert:插入 left:左边 right:右边 search:查找 string:字符串
修改前 insert:插入
修改后 insert:插入(动词)
删除search后字典:insert:插入(动词) left:左边 right:右边 string:字符串
单词出现次数统计:苹果:6 香蕉:2 西瓜:3测试结果表明,Key/Value 型二叉搜索树完美支持 "键值对" 的增删查改,且中序遍历按 Key 有序排列,满足字典、计数等场景的需求。
五、二叉搜索树的实际应用场景
二叉搜索树的核心优势是 "动态有序 + 高效增删查改",以下是其典型应用场景的详细解析:
5.1 关于Key 型场景的存在性验证
5.1.1 小区车库车牌验证
- 需求:仅允许已登记车牌的车辆进入车库,车辆入场时扫描车牌,验证是否在系统中;
- 实现:将所有登记车牌存储在 Key 型二叉搜索树中,扫描车牌后调用 Find 接口,存在则抬杆放行,否则拒绝;
- 优势:支持动态添加 / 删除车牌(如业主过户),插入和查找效率远高于数组。

5.1.2 单词拼写检查
- 需求:检查文章中单词拼写是否正确,错误单词标红提示;
- 实现:将词库中所有正确单词存储在 Key 型二叉搜索树中,遍历文章单词,调用 Find 接口验证,不存在则标红;
- 优势:词库可动态更新(添加新单词、删除废弃单词),查找效率高于线性结构。
5.2 Key/Value 型场景:映射与统计
5.2.1 简单中英互译字典
- 需求:输入英文单词,快速查询对应的中文释义,支持释义修改;
- 实现:使用 Key/Value 型二叉搜索树,Key 为英文单词,Value 为中文释义,Find 接口返回节点指针,可修改释义;
- 优势:按单词字母序排序(中序遍历),支持动态添加单词,查询效率高。
5.2.2 停车场计时收费
- 需求:车辆入场时记录车牌和入场时间,离场时计算停车时长并收费;
- 实现:Key 为车牌,Value 为入场时间。入场时 Insert(车牌,当前时间),离场时 Find 车牌获取入场时间,计算时长后 Erase 该记录;
- 优势:支持大量车辆同时入场离场,插入、查找、删除操作高效,无需额外排序。

5.2.3 文章单词计数
- 需求:统计文章中每个单词的出现次数,按单词排序输出;
- 实现:Key 为单词,Value 为计数。遍历单词时,Find 到则计数 + 1,未找到则 Insert(单词,1),中序遍历按单词排序输出计数;
- 优势:动态统计,无需提前知道所有单词,排序与统计一步完成。
六、二叉搜索树的缺陷与优化方向
6.1 核心缺陷:退化风险
二叉搜索树的最大问题是容易退化为单支树 。例如,当插入的节点序列为有序序列(如 1、2、3、4、5)时,树会退化为右单支树,此时所有操作的时间复杂度变为,完全失去优势。
6.2 优化方向:平衡二叉树
为了解决退化问题,需要通过特定机制维持树的平衡,确保树的高度始终保持在级别。常见的平衡二叉树包括:
- AVL 树:严格平衡二叉树,要求左右子树的高度差(平衡因子)不超过 1。插入和删除时通过旋转操作维持平衡,查询效率稳定,但旋转操作频繁,插入删除效率较低;
- 红黑树 :近似平衡二叉树,通过颜色规则(红节点不连续、黑平衡)维持平衡。插入和删除时旋转操作较少,综合效率高于 AVL 树,是 STL 中 set、map、multiset、multimap 的底层实现。
6.3 STL 中的二叉搜索树应用
C++ STL 中的 set、map、multiset、multimap 均是基于红黑树(平衡二叉搜索树)实现的,其设计思想与本文实现的二叉搜索树一脉相承:
- set/multiset:仅存储 Key,set 不允许重复 Key,multiset 允许重复 Key;
- map/multimap:存储 Key-Value 对,map 不允许重复 Key,multimap 允许重复 Key;
- 所有容器的迭代器遍历结果均为有序(中序遍历),支持高效的插入、查找、删除操作。
总结
通过本文对 C++ 二叉搜索树的全面拆解,我们不难发现其作为 "动态有序数据结构基石" 的核心定位。二叉搜索树以 "左子树≤根≤右子树" 的递归性质为核心,凭借中序遍历有序的特性,完美平衡了动态数据的增删查改需求,既弥补了二分查找在动态场景下的低效短板,也为后续 AVL 树、红黑树等平衡树的学习奠定了基础。
无论是日常开发中的动态数据处理,还是后续复杂数据结构的学习,二叉搜索树的核心思路都将持续发挥价值,希望本文能为大家的学习与实践提供切实的帮助。