文章目录
- [一 监督学习之外的机器学习](#一 监督学习之外的机器学习)
- [二 无监督学习:发现数据的内在结构](#二 无监督学习:发现数据的内在结构)
-
- [2.1 监督学习与无监督学习的对比](#2.1 监督学习与无监督学习的对比)
- [2.2 聚类的应用](#2.2 聚类的应用)
- [三 K-均值聚类算法 (K-means)](#三 K-均值聚类算法 (K-means))
-
- [3.1 K-均值算法的核心步骤](#3.1 K-均值算法的核心步骤)
- [3.2 K-均值算法的迭代过程演示](#3.2 K-均值算法的迭代过程演示)
- [3.3 K-均值算法伪代码](#3.3 K-均值算法伪代码)
- [3.4 K-均值的应用场景](#3.4 K-均值的应用场景)
- [四 K-均值算法的优化目标](#四 K-均值算法的优化目标)
-
- [4.1 代价函数:失真(Distortion)](#4.1 代价函数:失真(Distortion))
- [4.2 K-均值算法如何最小化代价函数](#4.2 K-均值算法如何最小化代价函数)
- [五 K-均值算法的实践要点](#五 K-均值算法的实践要点)
-
- [5.1 随机初始化与局部最优](#5.1 随机初始化与局部最优)
- [5.2 如何选择聚类数量 K](#5.2 如何选择聚类数量 K)
- [六 异常检测 (Anomaly Detection)](#六 异常检测 (Anomaly Detection))
-
- [6.1 异常检测的基本思想](#6.1 异常检测的基本思想)
- [6.2 异常检测的应用](#6.2 异常检测的应用)
- [6.3 基于高斯分布的异常检测算法](#6.3 基于高斯分布的异常检测算法)
- [6.4 异常检测算法的评估](#6.4 异常检测算法的评估)
视频链接
吴恩达机器学习p102-p111
一 监督学习之外的机器学习
到目前为止,我们课程的大部分内容都聚焦于监督学习(Supervised Learning)。然而,机器学习的领域远不止于此。

除了监督学习,还有其他几种主要的机器学习范式:
- 无监督学习 (Unsupervised Learning) :我们接下来将要深入探讨的领域,主要包括聚类(Clustering)和异常检测(Anomaly Detection)。
- 推荐系统 (Recommender Systems):广泛应用于电商、视频和音乐平台。
- 强化学习 (Reinforcement Learning):用于训练智能体(agent)在环境中通过试错来学习最优策略,常用于游戏和机器人控制。
二 无监督学习:发现数据的内在结构
2.1 监督学习与无监督学习的对比

首先,我们回顾一下监督学习。在监督学习中,我们的训练集由成对的输入x和对应的目标输出y组成,即 {(x^(1), y^(1)), (x^(2), y^(2)), ...}。我们的目标是学习一个从x到y的映射关系。

与此不同,在无监督学习 中,我们的训练集只有输入数据x,没有对应的标签y,即 {x^(1), x^(2), ...}。算法的目标不是预测一个标签,而是在数据中发现某种有趣的结构或模式。聚类(Clustering是无监督学习中最常见的任务之一,其目标是找到数据中自然形成的分组或"簇"。
2.2 聚类的应用

聚类算法在许多领域都有广泛的应用,例如:
- 新闻分组:自动将成千上万条关于同一事件的新闻报导聚合在一起。
- 市场细分:根据客户的行为和属性,将他们划分为不同的客户群体,以便进行精准营销。
- DNA分析:根据基因表达模式对个体进行分组。
- 天文数据分析:对星体进行分组,以确定哪些天体共同构成一个星系。
三 K-均值聚类算法 (K-means)
K-均值(K-means)是最流行和最广泛使用的聚类算法之一。
3.1 K-均值算法的核心步骤
K-均值算法是一个迭代的过程,它重复执行以下两个核心步骤:
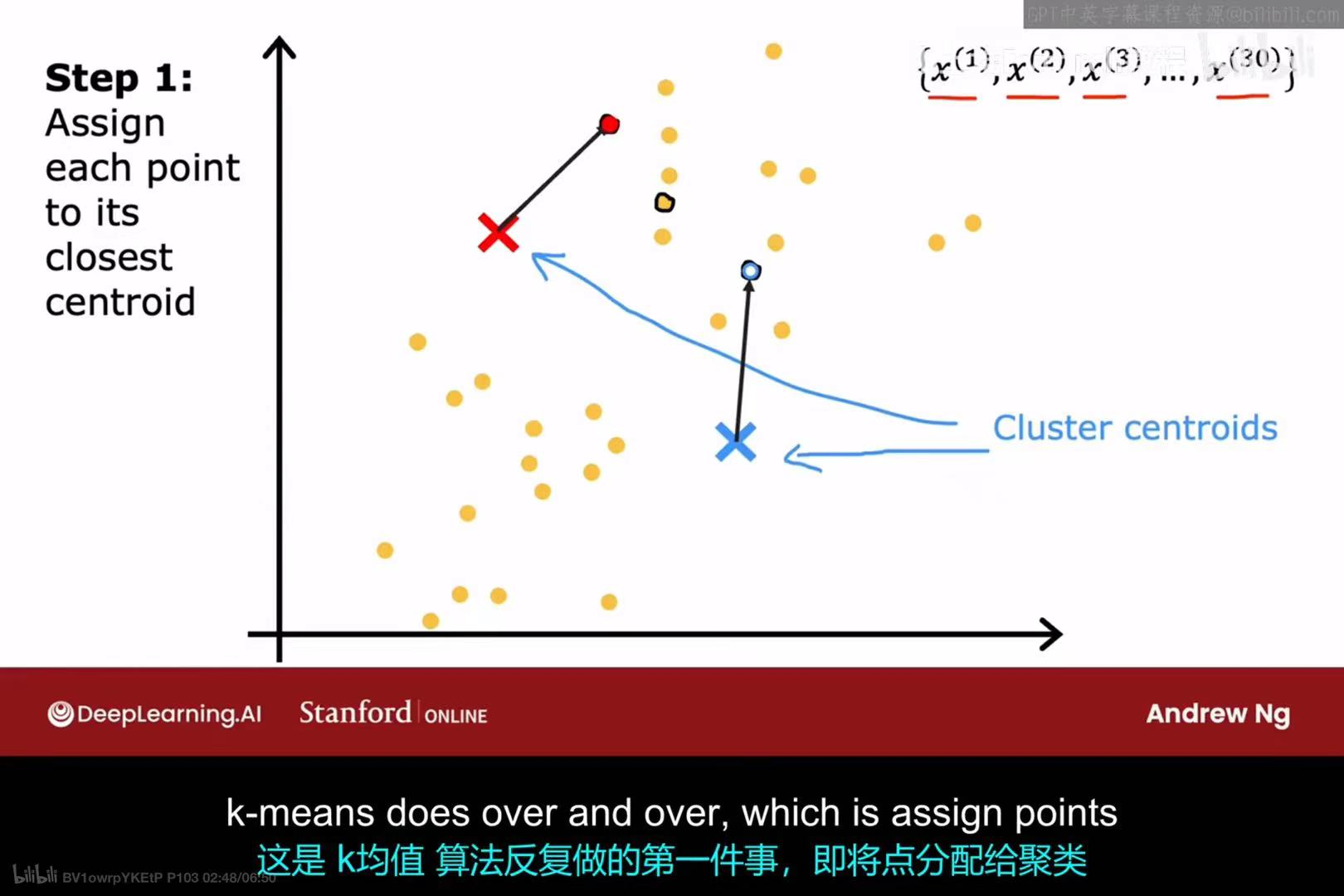
步骤 1:分配样本点 (Assign points)
- 对于数据集中的每一个样本点,计算它到每一个聚类中心(cluster centroids的距离。
- 将该样本点分配给距离它最近的那个聚类中心。
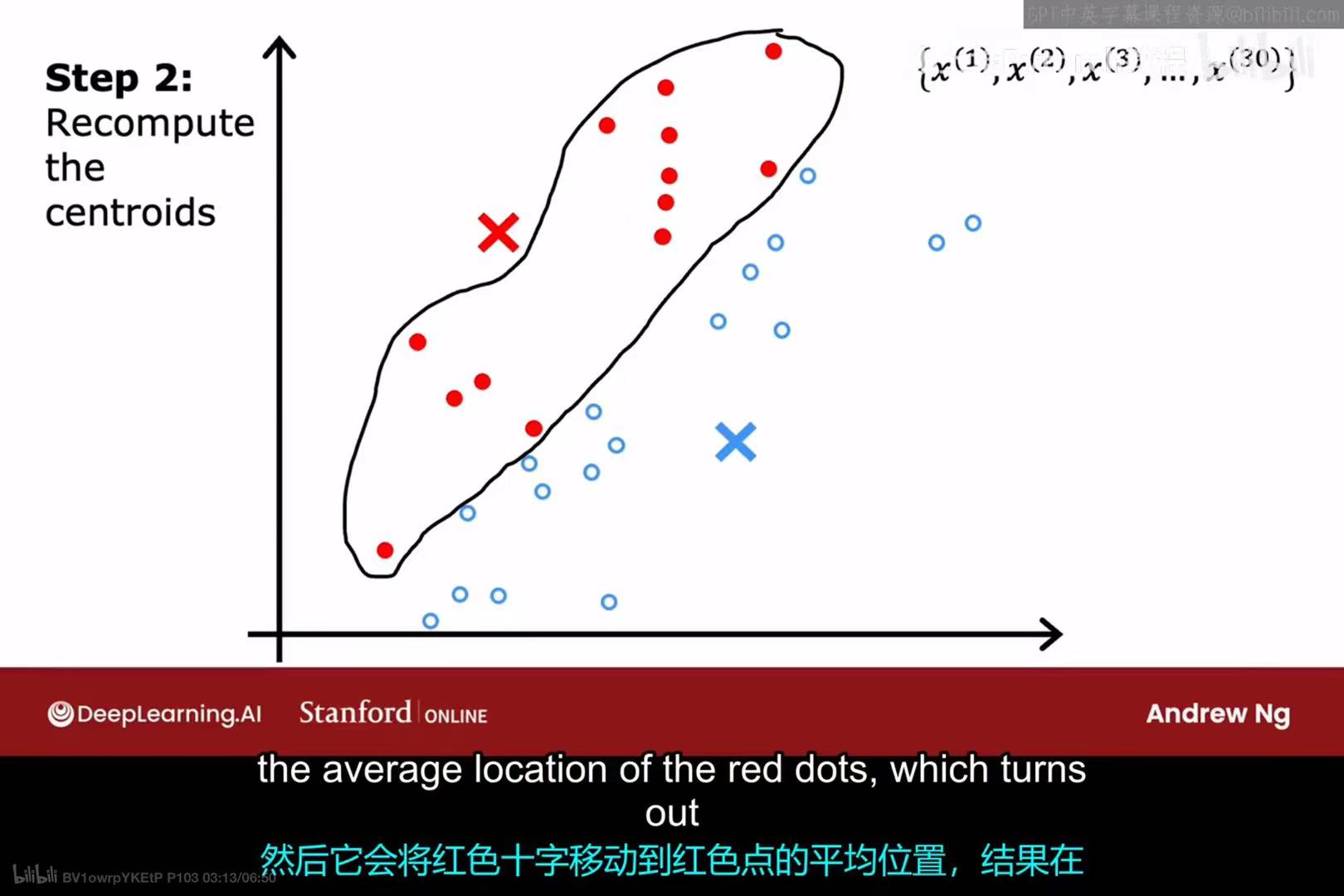
步骤 2:移动聚类中心 (Recompute the centroids)
- 对于每一个聚类中心,找出所有被分配给它的样本点。
- 将该聚类中心的位置移动到这些样本点的平均值(mean所在的位置。
算法会不断地重复这两个步骤,直到聚类中心的位置不再发生变化,或者变化非常小为止。
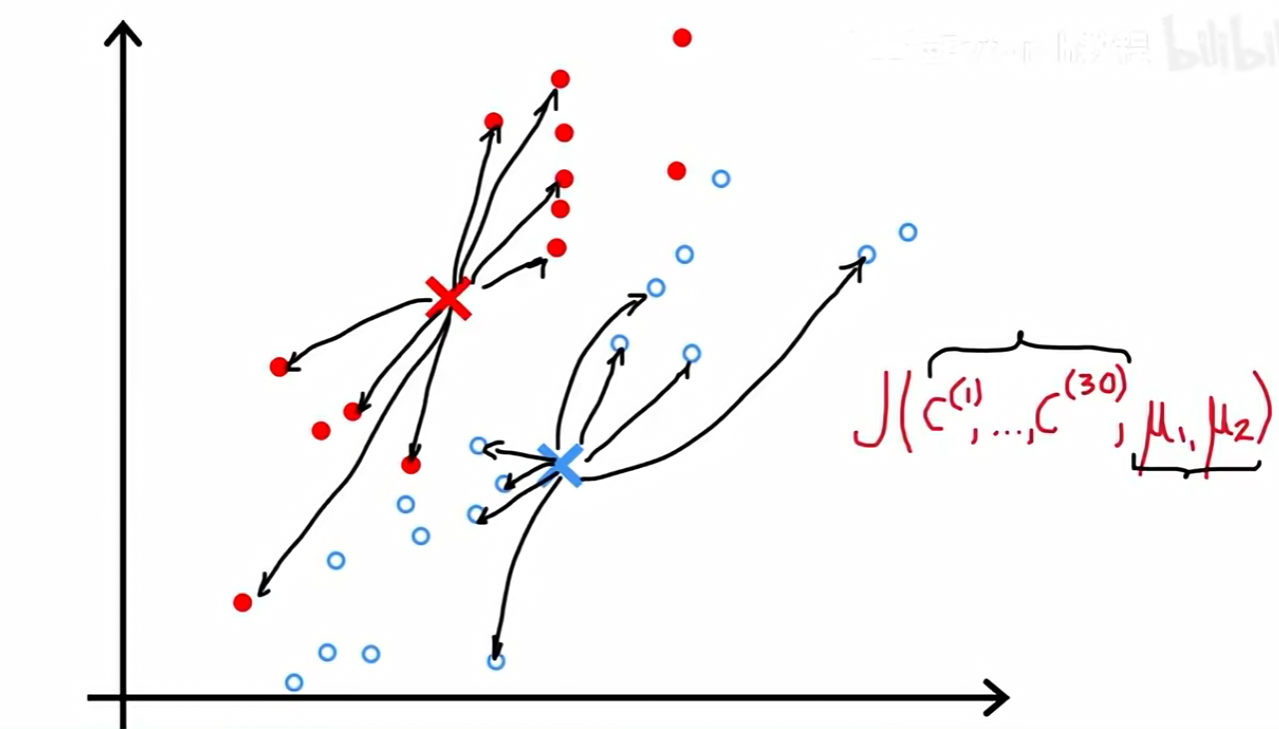
3.2 K-均值算法的迭代过程演示
让我们通过一个完整的迭代过程来理解算法的运作:
-
初始状态:随机初始化两个聚类中心(红色叉和蓝色叉)。
-
第一次迭代 - 步骤1 :
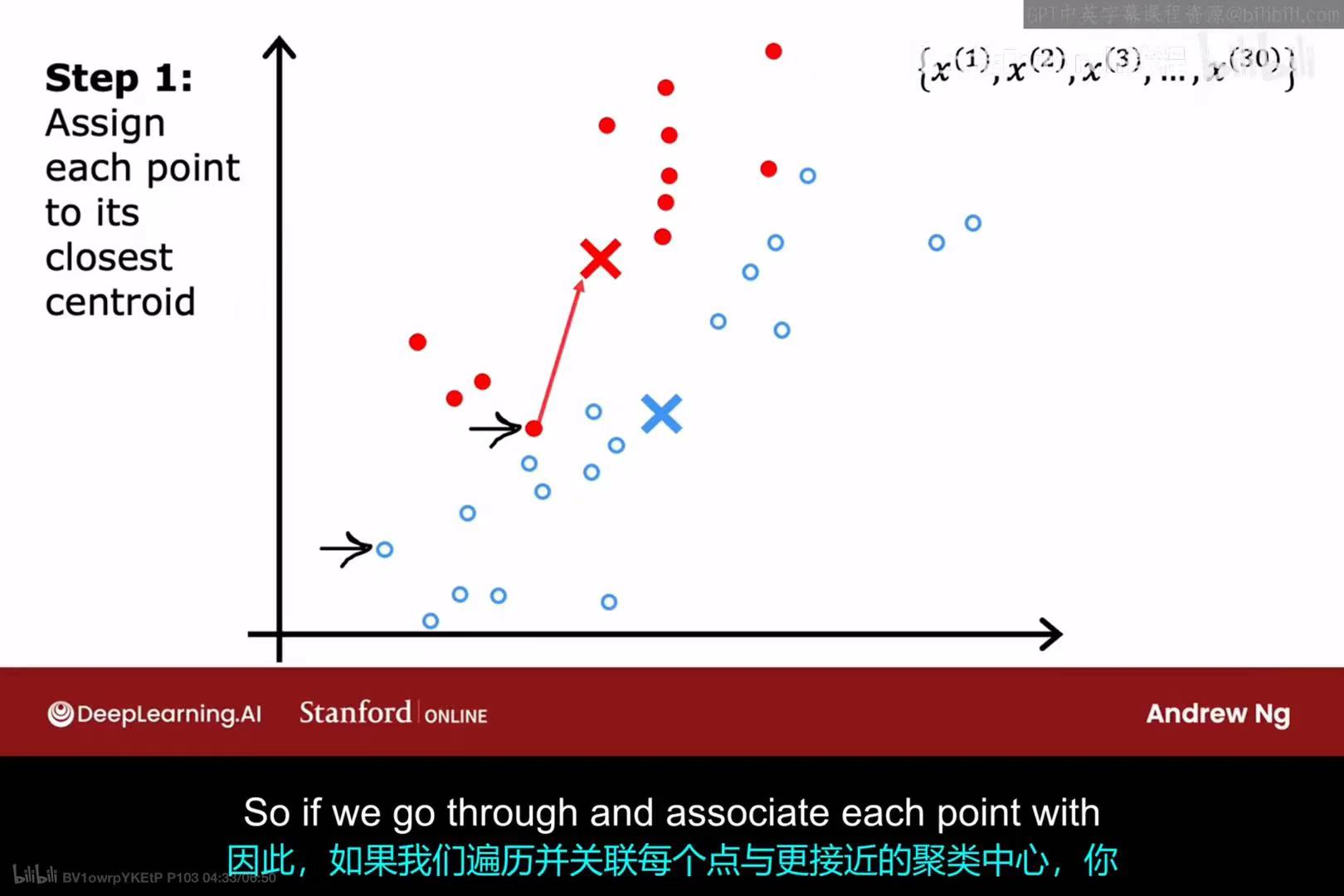
遍历所有样本点,并将它们分配给离自己最近的聚类中心。结果是,上半部分的点被染成红色,下半部分的点被染成蓝色。
-
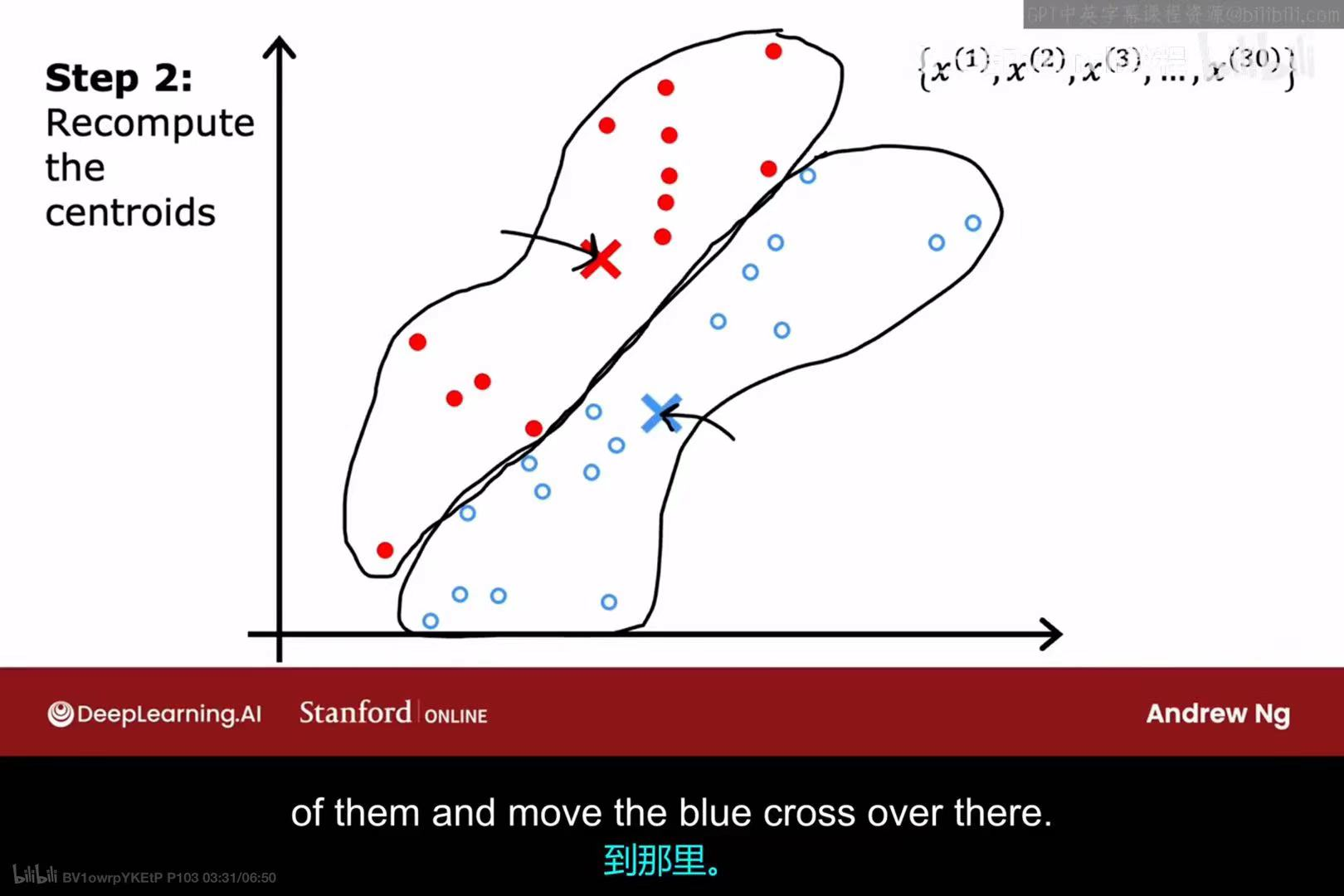
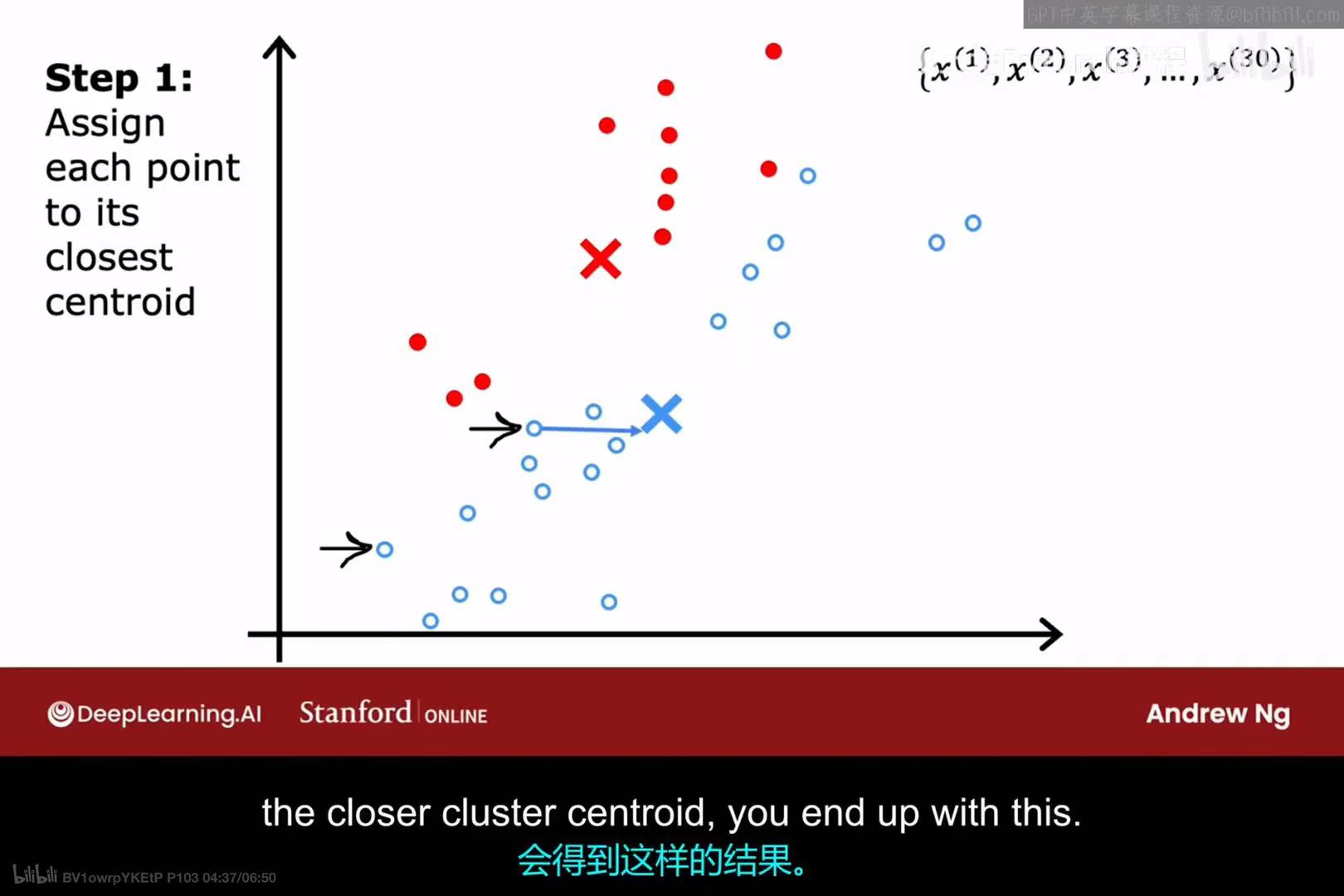
第一次迭代 - 步骤2 :

重新计算所有红点的平均位置,并将红色聚类中心移动到该位置。同样,计算所有蓝点的平均位置,并将蓝色聚类中心移动到那里。
-
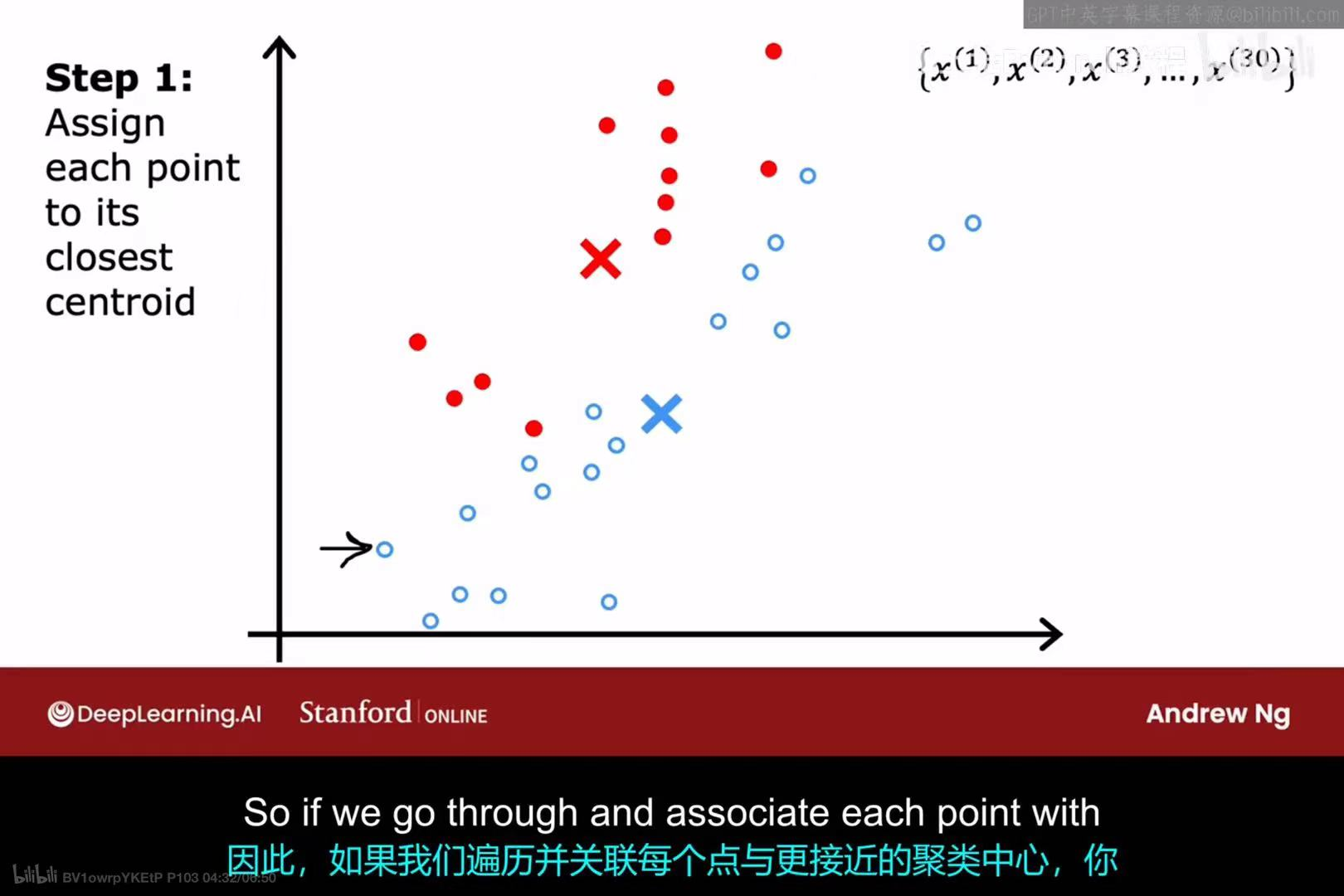
第二次迭代 - 步骤1 :
聚类中心移动后,样本点与它们的距离发生了变化。我们再次执行分配步骤,根据新的聚类中心位置,重新为每个样本点分配归属。
-
第二次迭代 - 步骤2 :
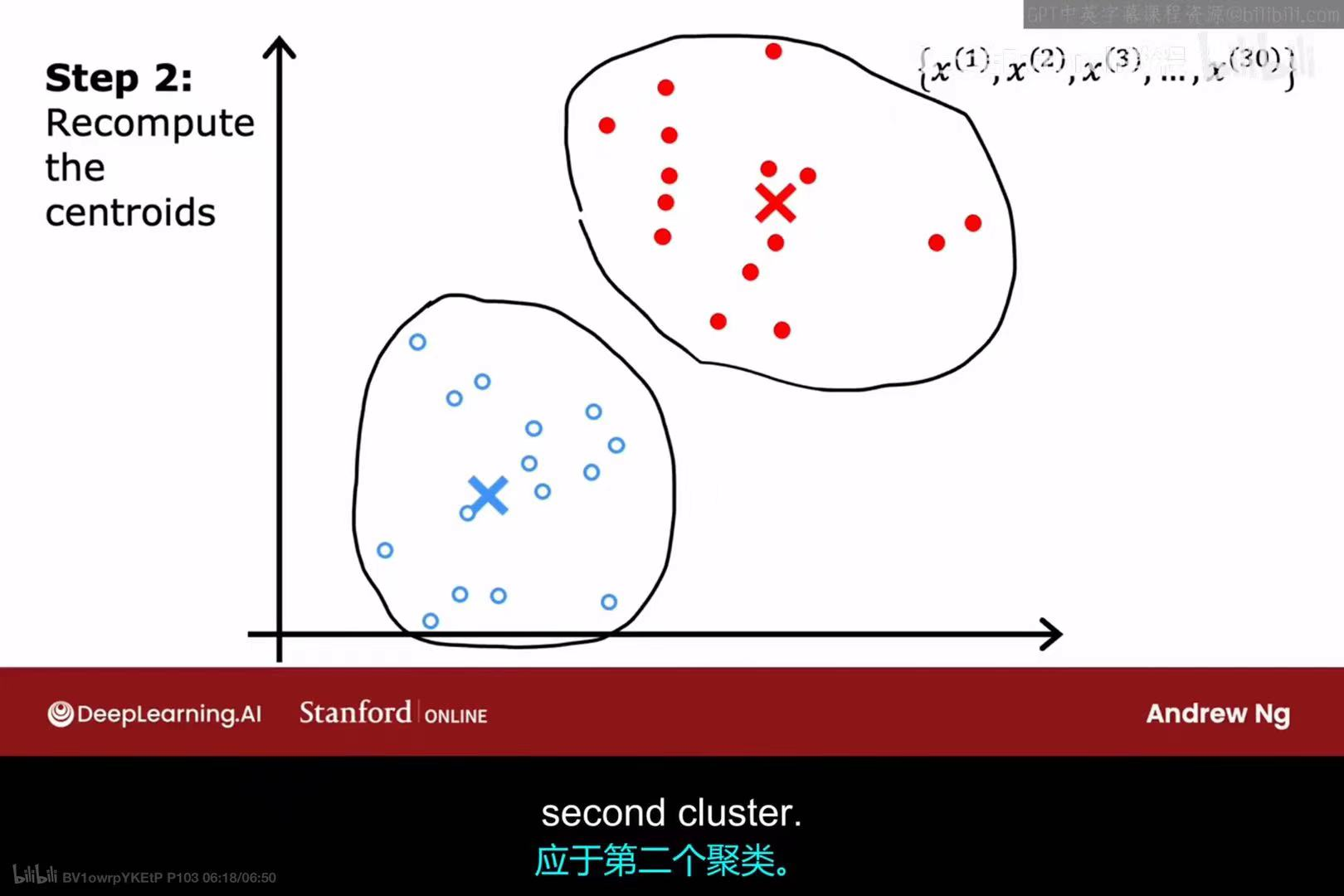
根据第二次分配的结果,再次计算每个簇的平均位置,并移动聚类中心。
经过几轮迭代后,聚类中心会稳定下来,最终将数据清晰地划分为两个簇。
3.3 K-均值算法伪代码

K-均值算法的流程可以总结为以下伪代码:
- 随机初始化
K个聚类中心μ₁, μ₂, ..., μₖ。 - 进入循环,重复以下操作:
- 分配步骤 :对于每一个样本
x^(i)(从i=1到m):- 计算
x^(i)到所有K个聚类中心的距离。 - 将
c^(i)设为距离x^(i)最近的那个聚类中心的索引。
- 计算
- 移动步骤 :对于每一个聚类
k(从k=1到K):- 将
μₖ更新为所有被分配到聚类k的样本点的平均值。
- 将
- 分配步骤 :对于每一个样本
3.4 K-均值的应用场景
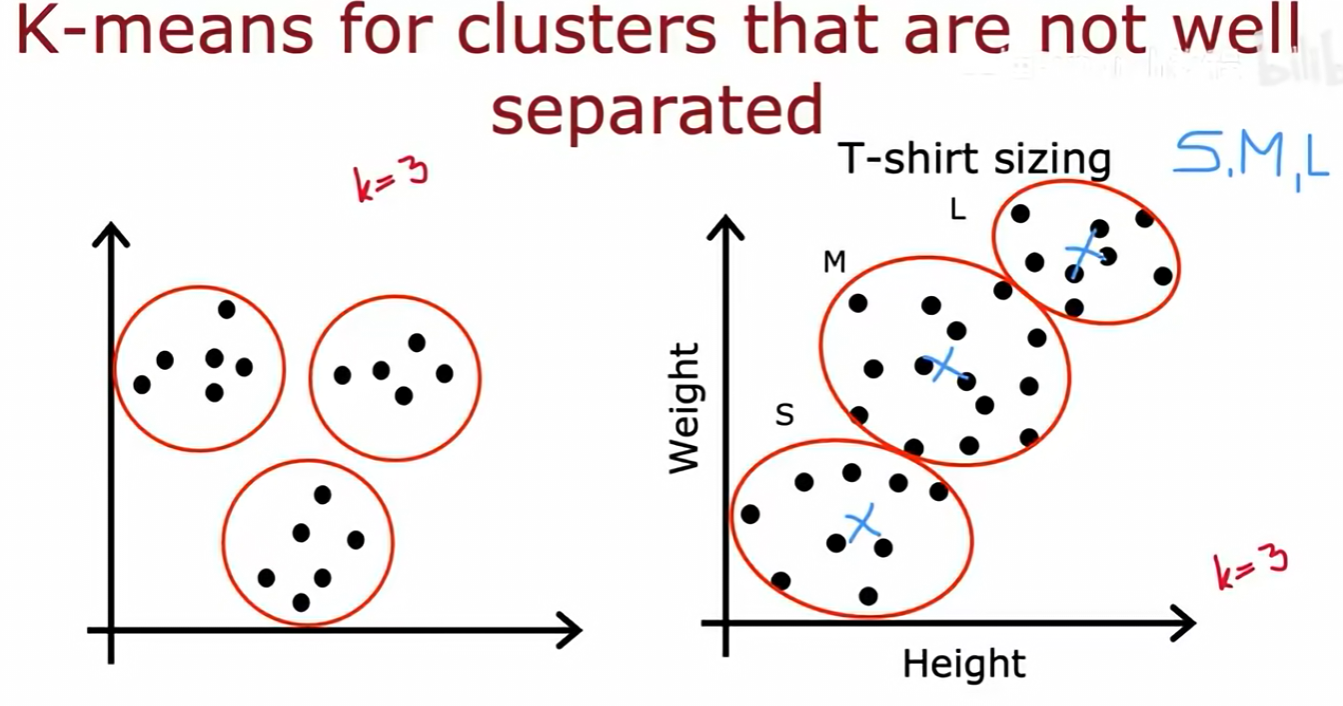
K-均值算法不仅能处理像左图那样分离清晰的簇,也能处理像右图那样相互重叠、边界不清晰的簇。例如,在T恤尺码设计中,我们可以收集大量用户的身高体重数据,然后使用K-均值(例如 K=3)将他们聚类,找到分别代表S、M、L三种尺码的"原型"身材,从而指导T恤的设计和生产。
四 K-均值算法的优化目标
K-均值算法的迭代过程实际上是在优化一个特定的数学目标,即最小化一个代价函数(Cost Function)。
4.1 代价函数:失真(Distortion)

K-均值算法的代价函数 J(也称为失真函数)被定义为:
- 数据集中每个样本点
x^(i)到其所属聚类中心μ_c^(i)之间距离的平方和的平均值。 - 公式:
J = (1/m) * Σ ||x^(i) - μ_c^(i)||^2 - 这个代价函数衡量了所有样本点到它们各自聚类中心的紧凑程度。
J的值越小,说明聚类的效果越好,簇内的点越密集。
4.2 K-均值算法如何最小化代价函数
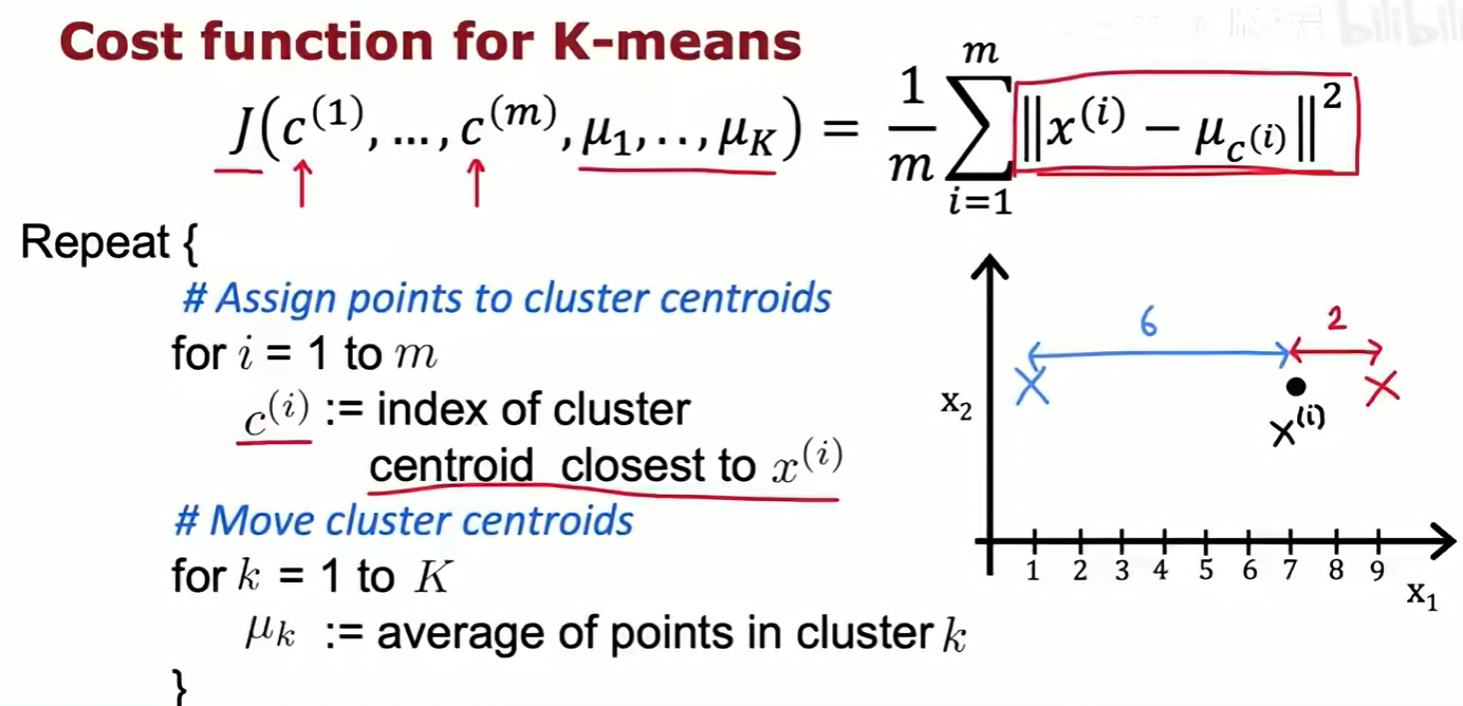
K-均值算法的两个步骤分别对应了对代价函数 J 的两个不同部分的最小化:
- 分配步骤(Assign points) :在保持聚类中心
μ不变的情况下,通过调整每个样本点的归属c^(i)来最小化J。显然,将每个x^(i)分配给离它最近的μ会使||x^(i) - μ_c^(i)||^2这一项最小。 - 移动步骤(Move centroids) :在保持样本归属
c不变的情况下,通过调整聚类中心μₖ的位置来最小化J。可以从数学上证明,将μₖ设为该簇内所有点的平均值,可以使与该簇相关的平方和项最小。
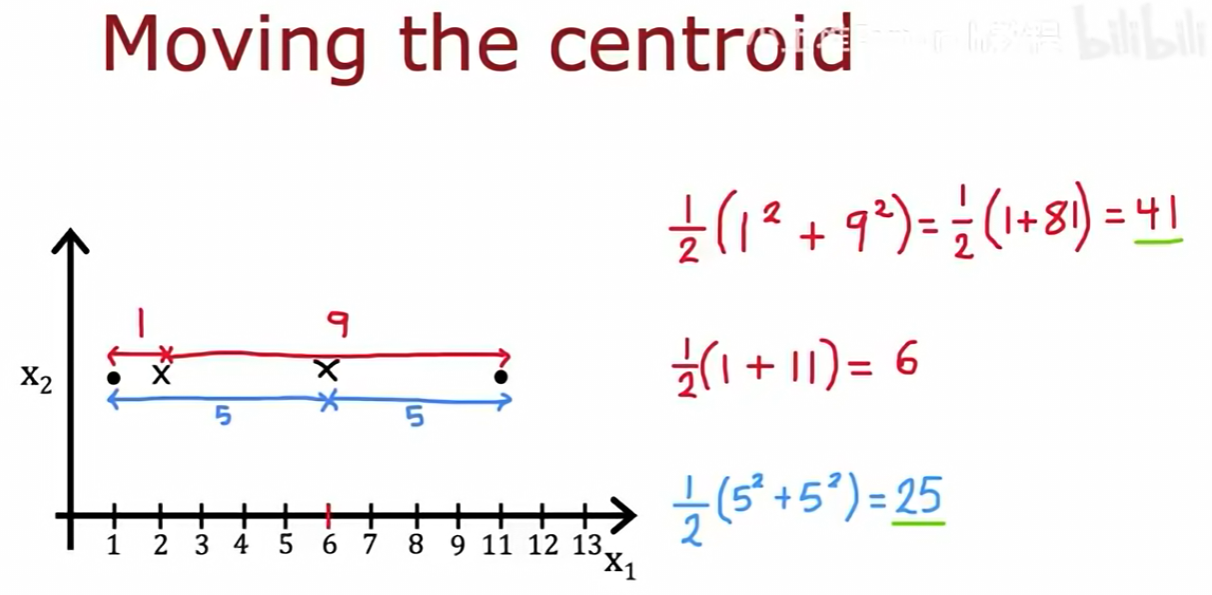
上图用一个一维的例子直观地说明了为什么均值是最佳选择。对于一组点,将中心点设为它们的均值,可以使到各点距离的平方和最小。
五 K-均值算法的实践要点
5.1 随机初始化与局部最优


K-均值算法的最终结果依赖于聚类中心的初始位置。
- 初始化方法 :一个常用的方法是从
m个训练样本中随机选择K个,并将这K个样本的位置作为初始的聚类中心位置。 - 问题 :不同的随机初始化可能会导致K-均值算法收敛到不同的最终聚类结果,其中一些可能是局部最优解,而不是全局最优解。
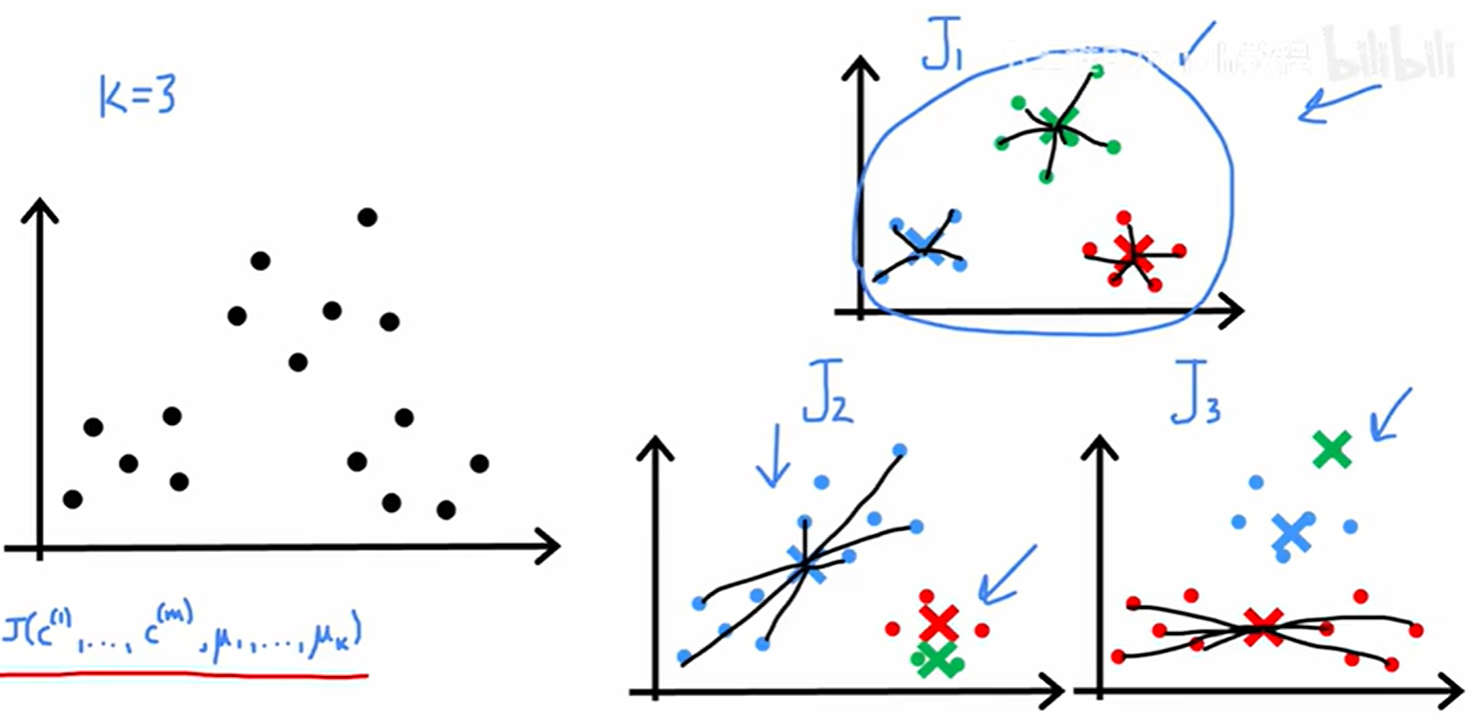
如上图所示,对于同一份数据,一次好的初始化(J₁)可能得到理想的聚类结果和很低的代价 J,而一次不好的初始化(J₂, J₃)可能会得到很差的聚类结果和较高的代价 J。

解决方案:
- 多次运行K-均值算法(通常是50到1000次)。
- 在每次运行中,都使用一组新的随机初始化的聚类中心。
- 对每一次运行得到的最终聚类结果,计算其代价函数
J的值。 - 最后,选择所有运行中代价
J最小的那一组聚类结果作为最终答案。
5.2 如何选择聚类数量 K
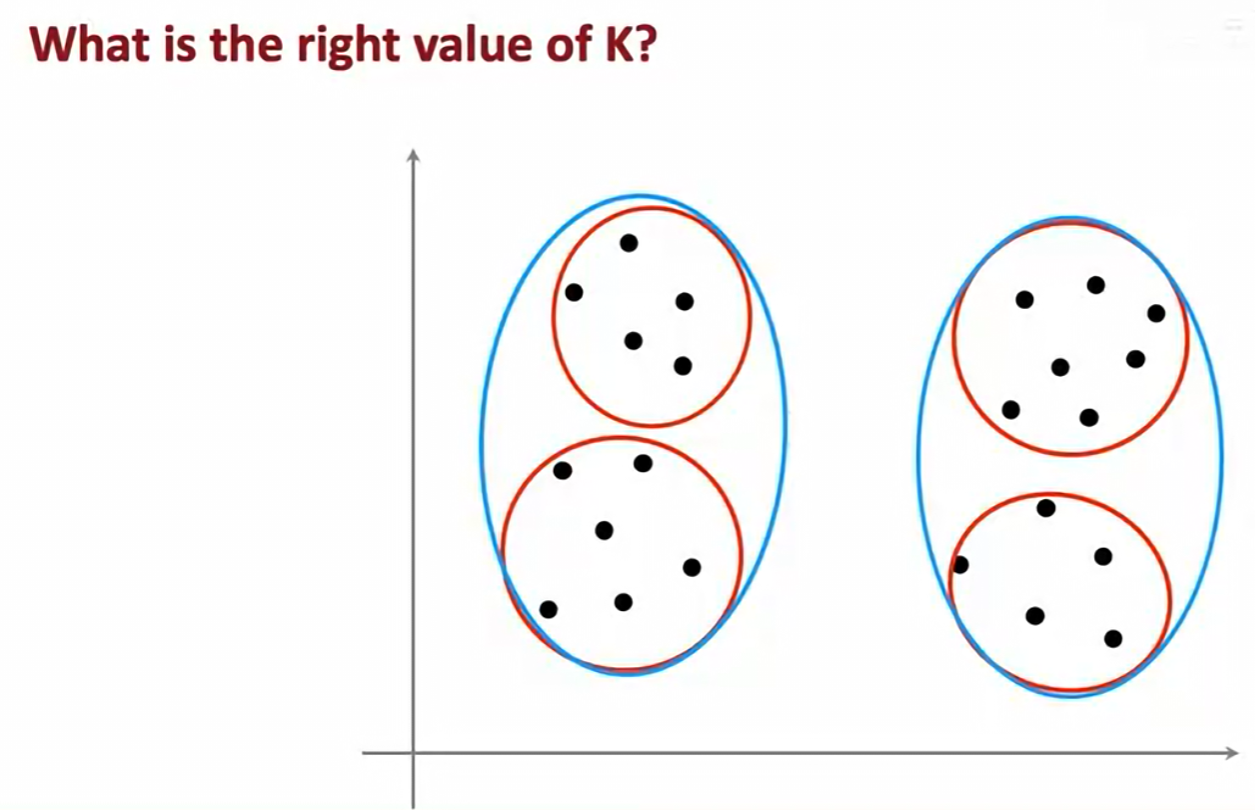
K-均值算法需要我们预先指定聚类的数量 K。但如何确定最佳的 K 值呢?
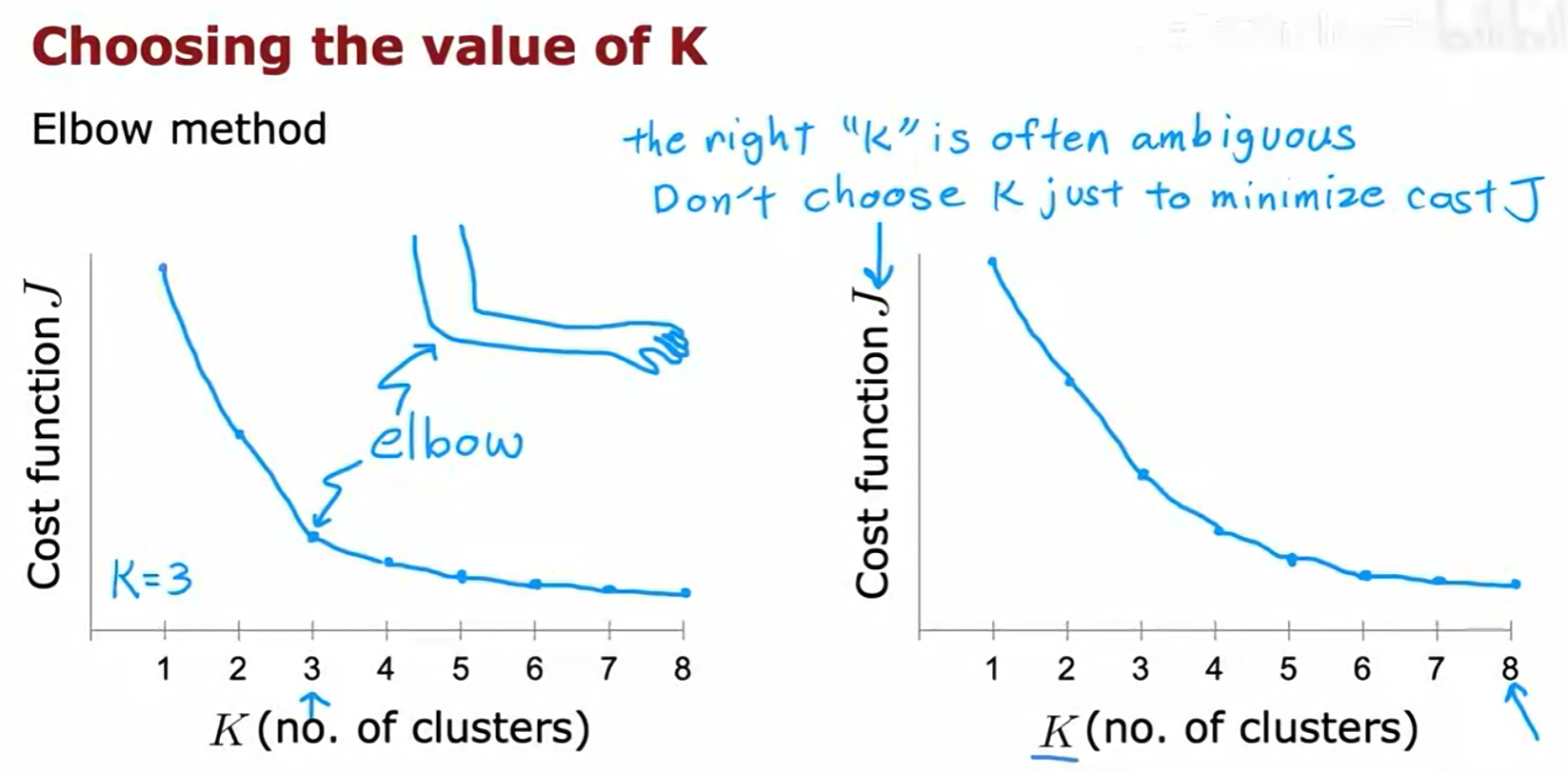
1. 肘部法则 (Elbow Method)
- 方法 :分别用不同的
K值(例如从1到10)运行K-均值算法,并计算出每个K值对应的最低代价J。然后,将J与K的关系绘制成图。 - 解读 :随着
K的增加,代价J总是会下降。我们寻找的是图中的"肘部"(Elbow),即J值急剧下降后变得平缓的那个点。这个点通常被认为是K的一个合理选择。 - 局限性:很多时候,代价曲线并没有一个清晰的"肘部",这使得该方法具有一定的主观性和模糊性。
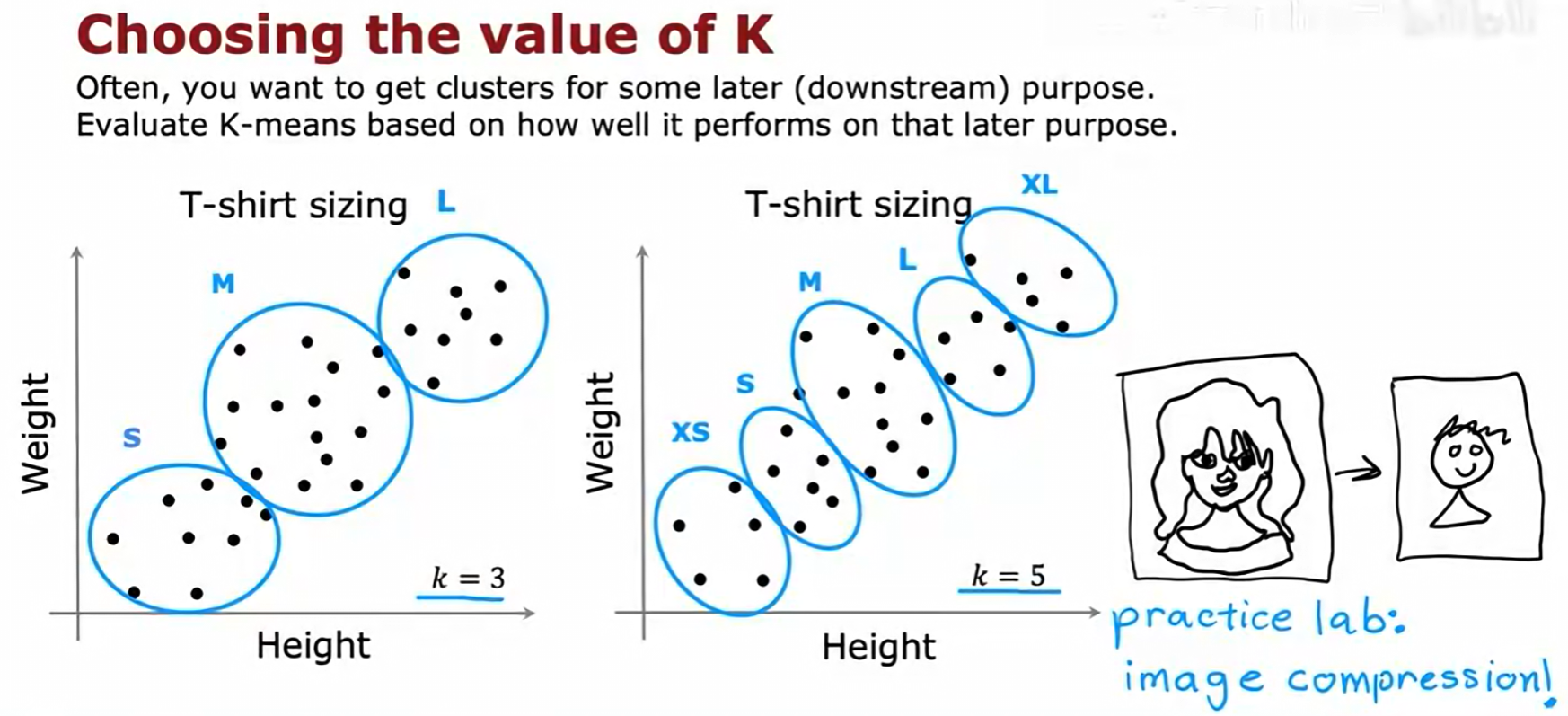
2. 评估下游指标
- 核心思想 :选择
K的更有效的方法,是看哪个K值能更好地服务于我们进行聚类的最终目的(下游任务)。 - 例子 :在T恤尺码的例子中,我们可以分别尝试
K=3和K=5。然后评估哪种聚类结果能带来更好的商业表现,例如,K=5(增加了XS和XL码)是否能更好地满足客户需求并提升销量。最终,我们应该选择那个对下游任务最有帮助的K值。
六 异常检测 (Anomaly Detection)
异常检测是无监督学习的另一个重要分支,其目标是识别出与"正常"数据显著不同的"异常"数据点。
6.1 异常检测的基本思想
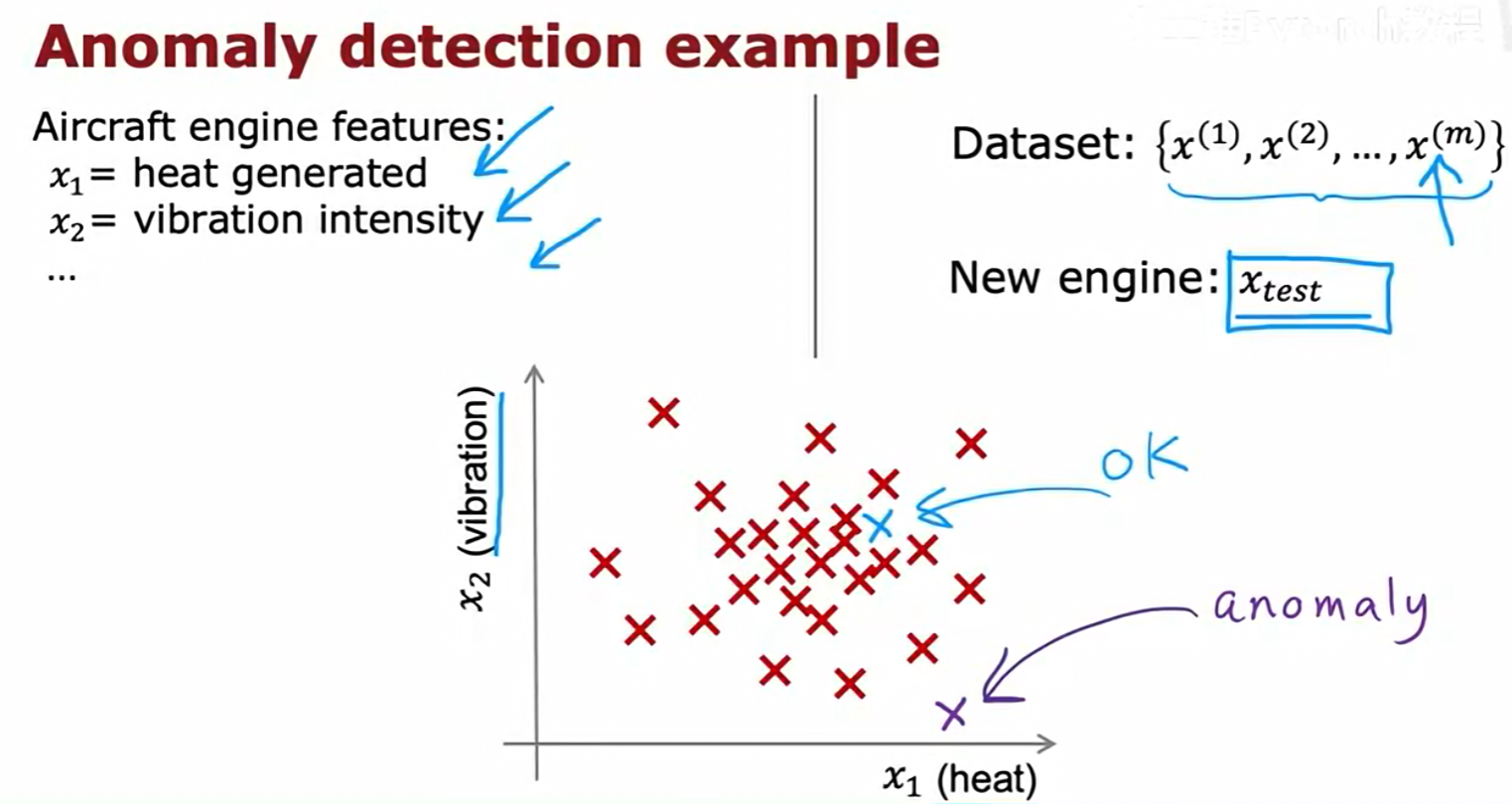
以飞机引擎监控为例,我们拥有大量描述正常引擎运行状态的数据(如产生的热量 x₁、振动强度 x₂ 等)。当一个新的引擎 x_test 出现时,我们的任务是判断它的状态是否异常。
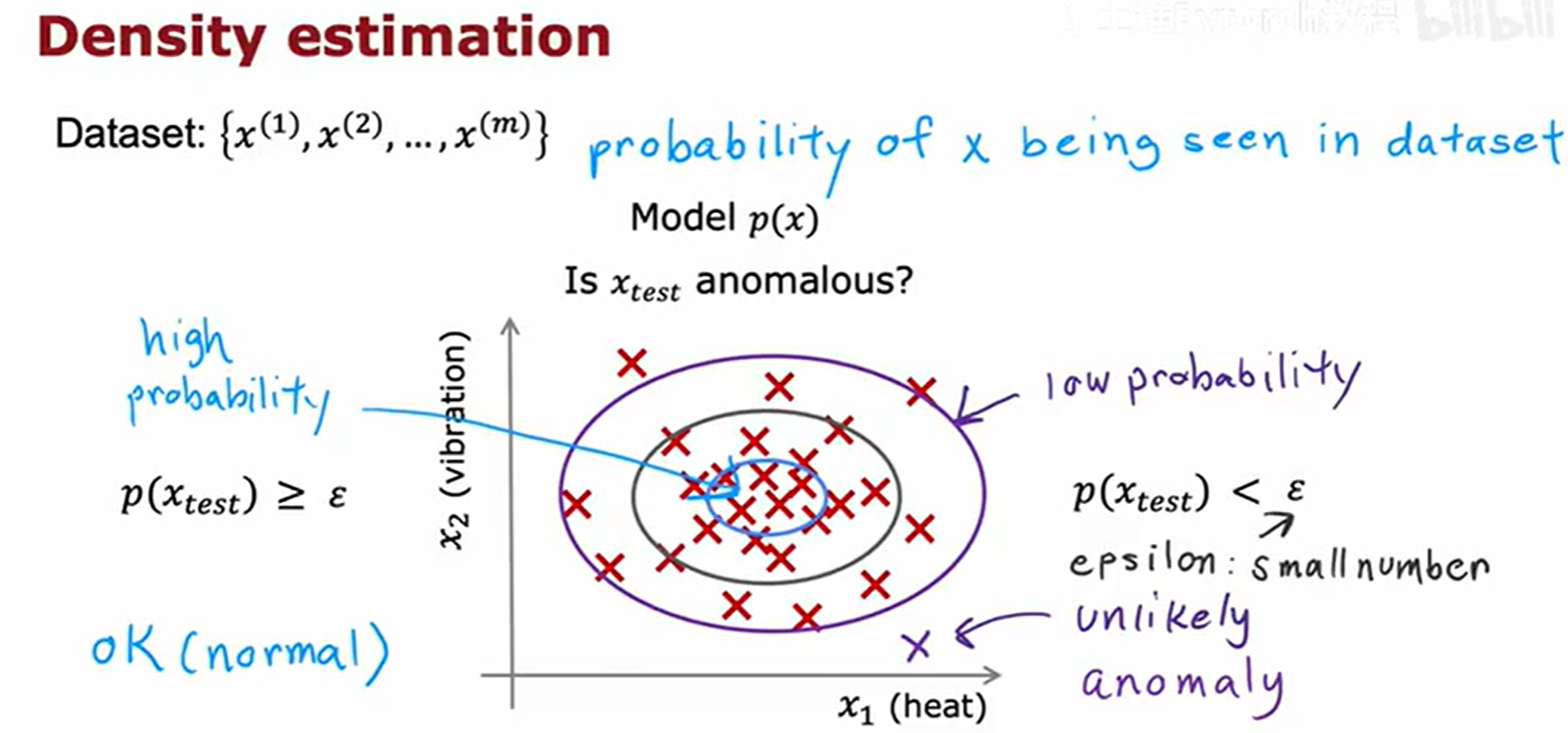
异常检测的核心方法是密度估计(Density Estimation):
- 我们首先使用大量的正常样本数据来学习一个概率模型
p(x)。这个模型描述了正常数据点的概率分布。 - 对于一个新的测试样本
x_test,我们计算它在这个模型下的概率p(x_test)。 - 判断 :
- 如果
p(x_test)很高,说明x_test与正常数据的分布很吻合,它是一个正常(ok样本。 - 如果
p(x_test)非常低(低于我们设定的一个阈值ε),说明x_test是一个在正常数据集中不太可能出现的点,它被判定为异常(anomaly)。
- 如果
6.2 异常检测的应用
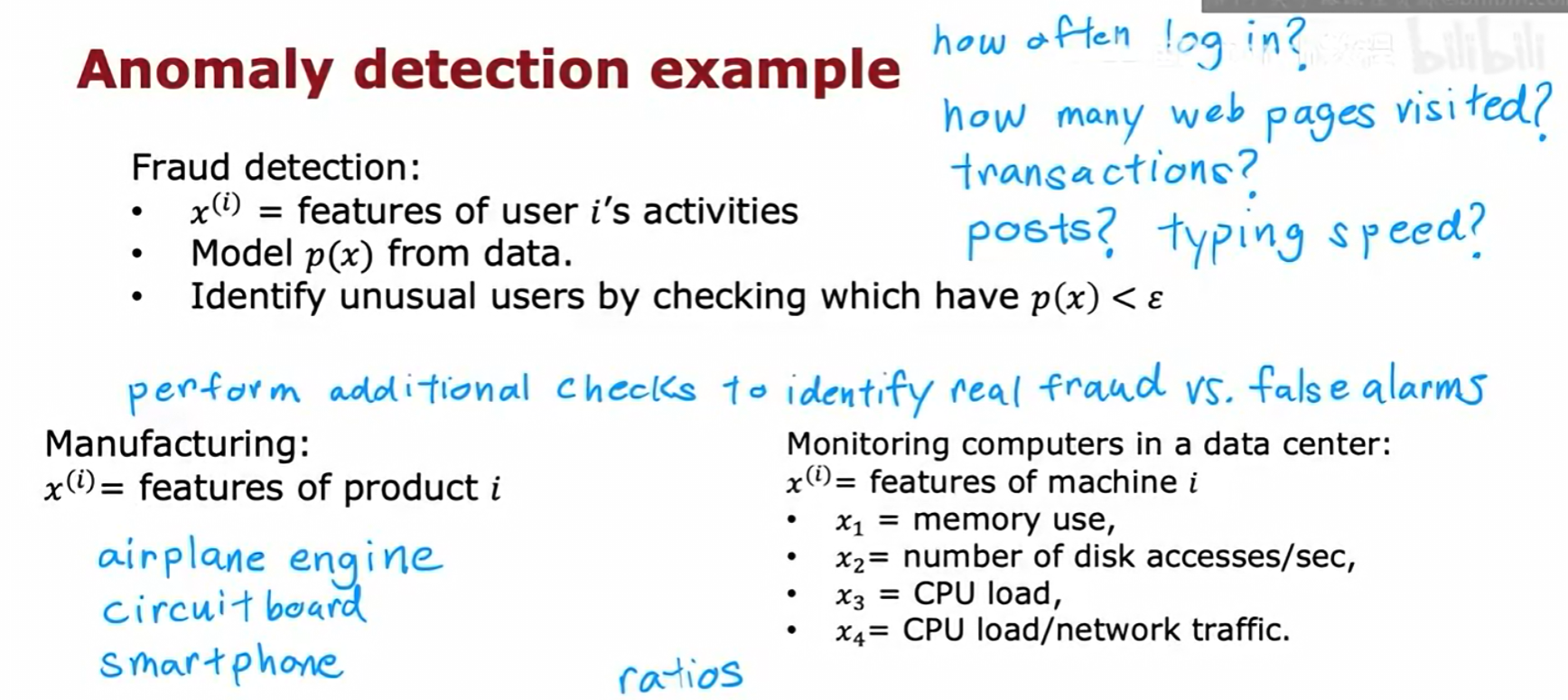
异常检测有许多实际应用:
- 欺诈检测 :通过分析用户的行为特征(登录频率、交易模式、打字速度等),建立正常用户行为模型
p(x),并识别出行为概率极低的异常用户。 - 制造业:监控产品(如飞机引擎、电路板)的各项指标,识别出可能存在缺陷的次品。
- 数据中心监控:监控服务器的特征(内存使用、CPU负载等),及时发现可能出现故障的机器。
6.3 基于高斯分布的异常检测算法
一个常用且有效的密度估计方法是假设数据特征服从高斯分布(Gaussian Distribution),也称正态分布。
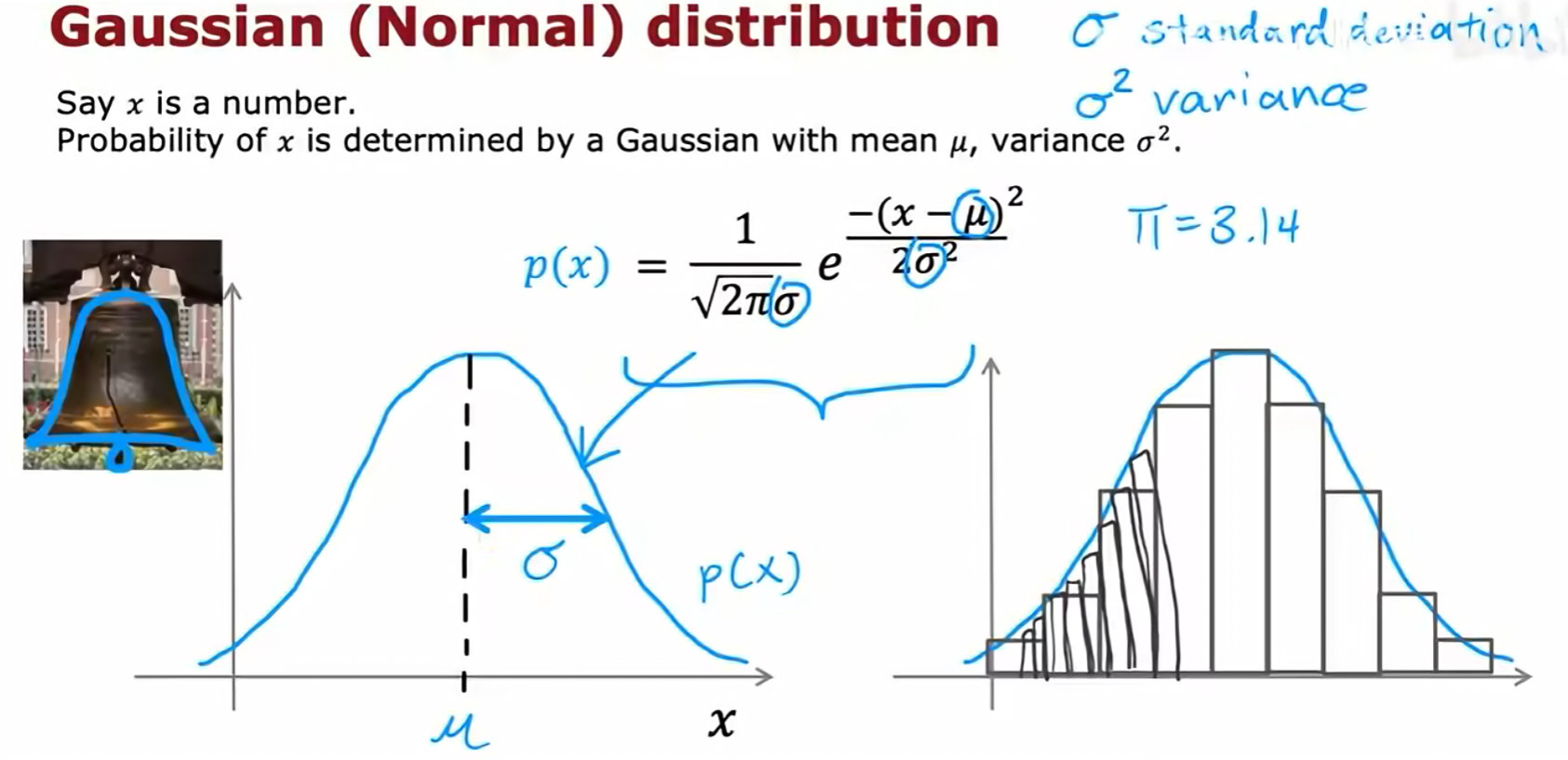
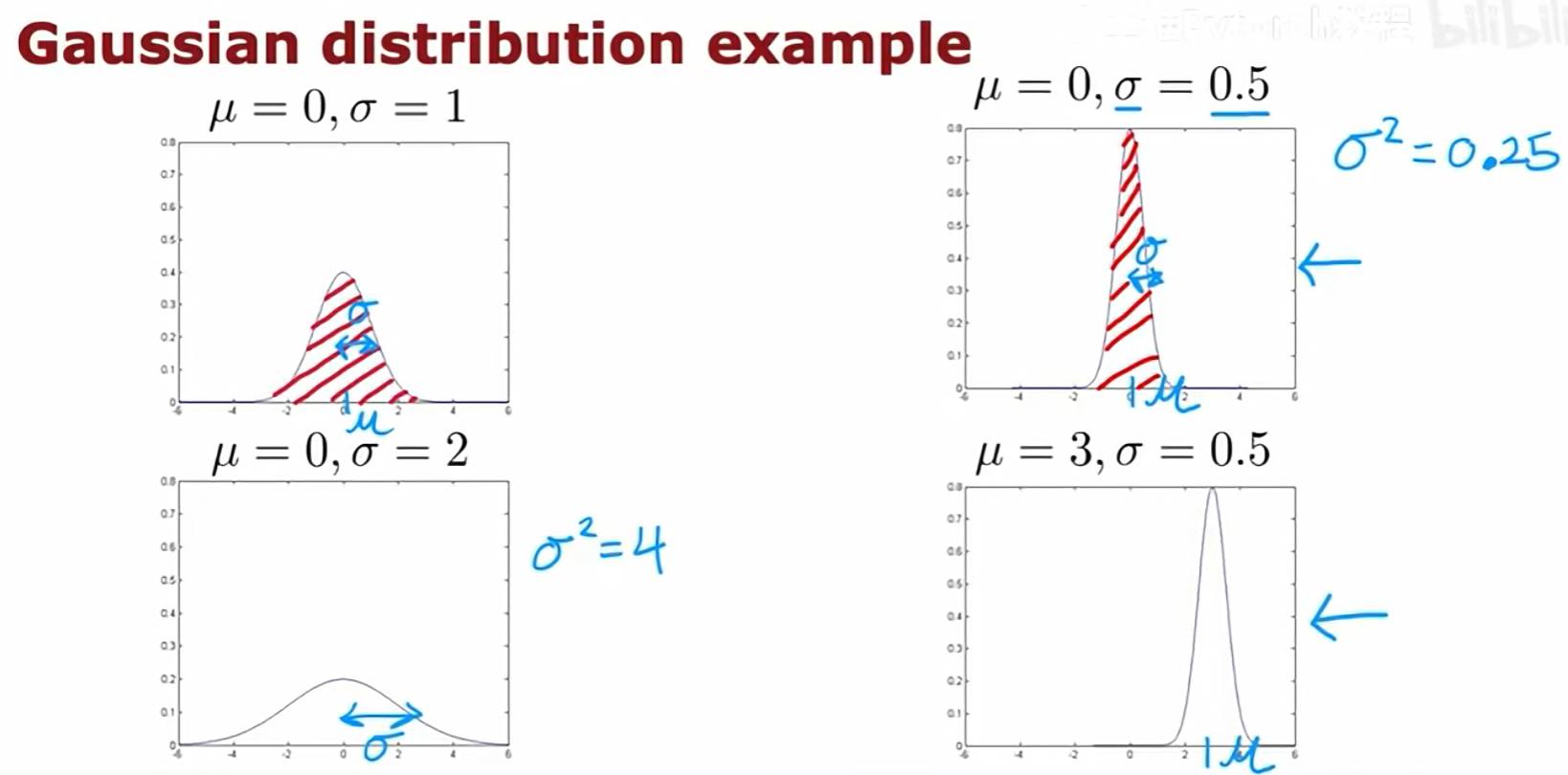
高斯分布由两个参数决定:均值 μ(决定了分布的中心位置)和方差 σ²(决定了分布的宽度)。σ 是标准差。
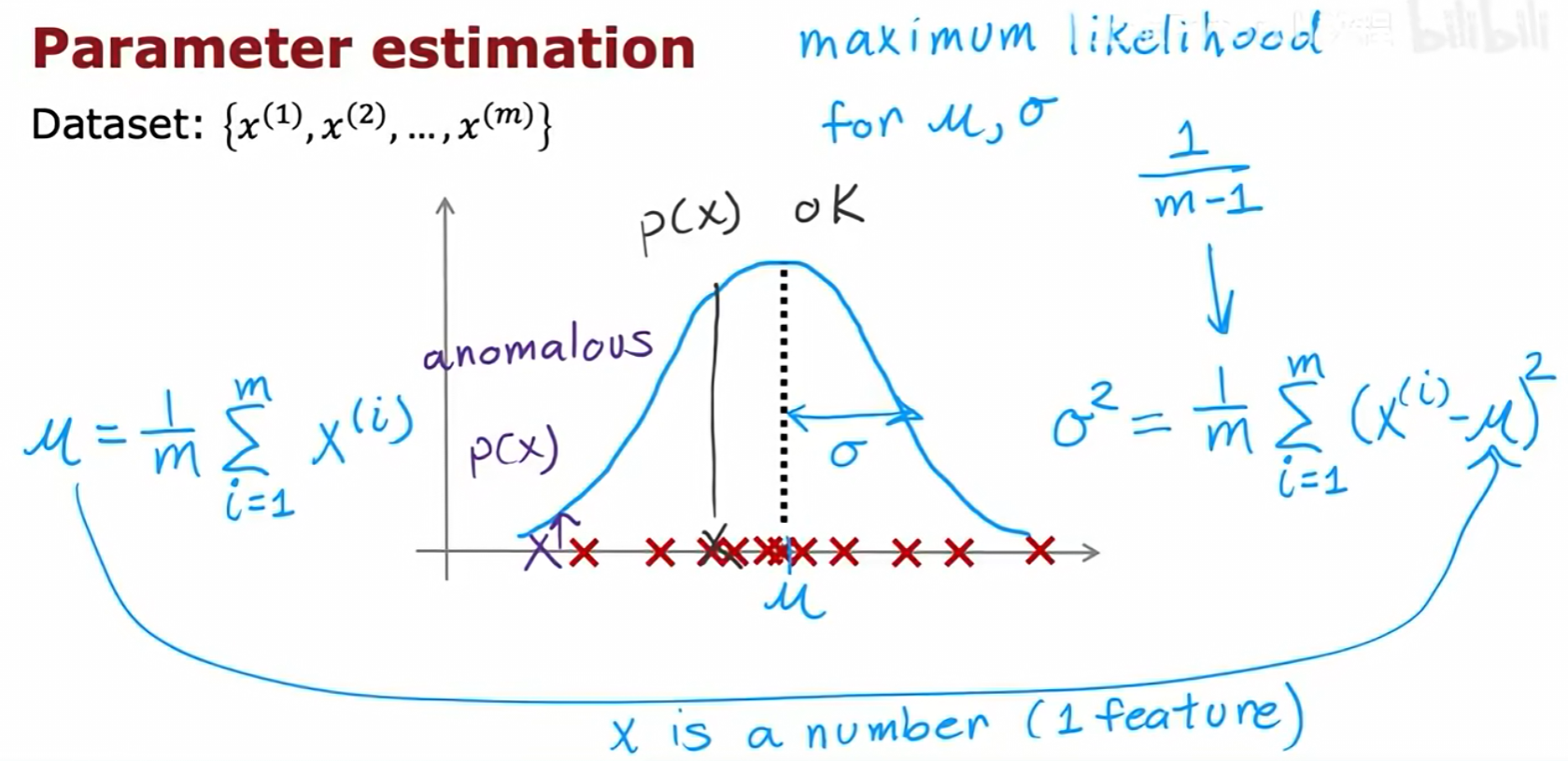
参数估计:对于一个给定的只包含正常样本的数据集,我们可以通过以下公式来估计每个特征的高斯分布参数(这对应于最大似然估计):
- 均值
μ:(1/m) * Σ x^(i) - 方差
σ²:(1/m) * Σ (x^(i) - μ)²(在机器学习中,分母通常用m而非m-1)

多维特征处理 :当数据有 n 个特征时,一个简化的假设(尽管在实际中不一定成立,但常常效果不错)是各个特征之间相互独立 。基于此假设,一个样本 x 的联合概率 p(x) 可以通过将它在每个特征上的边缘概率相乘得到:
p(x) = p(x₁) * p(x₂) * ... * p(xₙ) = Π p(xⱼ; μⱼ, σⱼ²)

算法总结:
- 选择
n个你认为可能指示异常的特征xⱼ。 - 使用正常样本的训练集,为每个特征
j估计参数μⱼ和σⱼ²。 - 对于一个新样本
x,使用高斯分布公式和独立性假设,计算其总概率p(x)。 - 如果
p(x) < ε,则将其标记为异常。
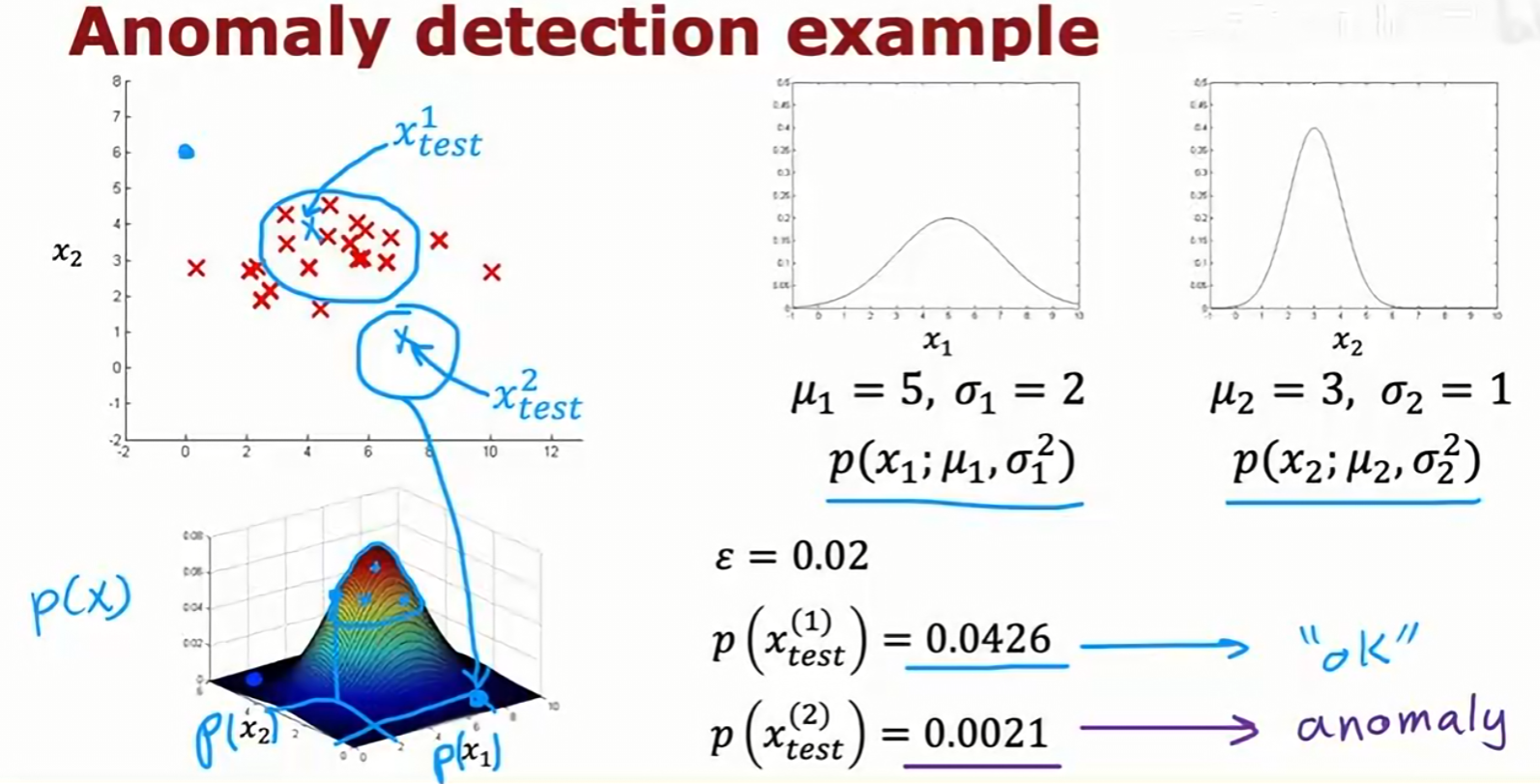
上图展示了一个二维的例子。通过为 x₁ 和 x₂ 分别建立高斯模型,我们可以计算出二维空间中任意一点的概率 p(x)。图中 x_test^(1) 位于概率高的中心区域,被判为正常;而 x_test^(2) 位于概率低的边缘区域,被判为异常。
6.4 异常检测算法的评估
尽管异常检测算法的训练过程是无监督的(只使用正常样本),但为了评估其性能和选择超参数(如阈值ε),我们通常需要一些带标签的数据。

数据划分策略:
- 训练集 :包含大量的正常样本 (
y=0)。用于学习概率模型p(x)。 - 交叉验证集 (CV) 和 测试集 :包含大量的正常样本(
y=0),并混入一小部分已知的异常样本 (y=1)。

评估流程:
- 由于CV集和测试集是高度偏斜的数据集(异常样本非常少)。
- 因此,我们不应该使用准确率作为评估指标。

- 正确的评估指标 :应该使用我们之前学过的精确率/召回率 和F1分数。
- 超参数调优 :在训练集上拟合好
p(x)模型后,我们在交叉验证集 上尝试不同的阈值ε,并选择那个能够使F1分数最高的ε作为最终的参数。然后在测试集上报告最终的性能。