《P6772 [NOI2020] 美食家》

题目描述

坐落在 Bzeroth 大陆上的精灵王国击退地灾军团的入侵后，经过十余年的休养生息，重新成为了一片欣欣向荣的乐土，吸引着八方游客。小 W 是一位游历过世界各地的著名美食家，现在也慕名来到了精灵王国。

精灵王国共有 n 座城市，城市从 1 到 n 编号，其中城市 i 的美食能为小 W 提供 ci 的愉悦值。精灵王国的城市通过 m 条单向道路连接，道路从 1 到 m 编号，其中道路 i 的起点为城市 ui ，终点为城市 vi，沿它通行需要花费 wi 天。也就是说，若小 W 在第 d 天从城市 ui 沿道路 i 通行，那么他会在第 d+wi 天到达城市 vi。

小 W 计划在精灵王国进行一场为期 T 天的旅行，更具体地：他会在第 0 天从城市 1 出发，经过 T 天的旅行，最终在恰好第 T 天 回到城市 1 结束旅行。由于小 W 是一位美食家，每当他到达一座城市时（包括第 0 天和第 T 天的城市 1），他都会品尝该城市的美食并获得其所提供的愉悦值，若小 W 多次到达同一座城市，他将获得多次愉悦值 。注意旅行途中小 W 不能在任何城市停留，即当他到达一座城市且还未结束旅行时，他当天必须立即从该城市出发前往其他城市。

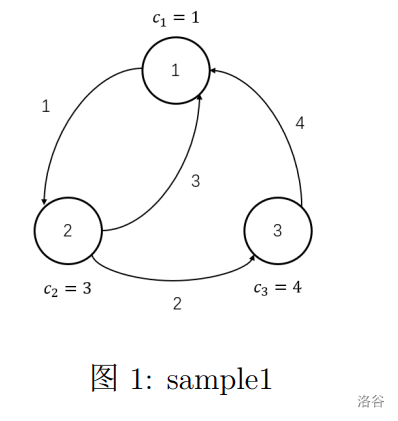
对于上图，小 W 一种为期 11 天的可行旅游方案为 1→2→1→2→3→1：

第 0 天，小 W 从城市 1 开始旅行，获得愉悦值 1 并向城市 2 出发。
第 1 天，小 W 到达城市 2，获得愉悦值 3 并向城市 1 出发。
第 4 天，小 W 到达城市 1，获得愉悦值 1 并向城市 2 出发。
第 5 天，小 W 到达城市 2，获得愉悦值 3 并向城市 3 出发。
第 7 天，小 W 到达城市 3，获得愉悦值 4 并向城市 1 出发。
第 11 天，小 W 到达城市 1，获得愉悦值 1 并结束旅行。
小 W 在该旅行中获得的愉悦值之和为 13。

此外，精灵王国会在不同的时间举办 k 次美食节。具体来说，第 i 次美食节将于第 ti 天在城市 xi 举办，若小 W 第 ti 天时恰好在城市 xi，那么他在品尝城市 xi 的美食时会额外得到 yi 的愉悦值。现在小 W 想请作为精灵王国接待使者的你帮他算出，他在旅行中能获得的愉悦值之和的最大值。

输入格式

从标准输入中读入数据。

第一行四个整数 n,m,T,k，依次表示城市数、道路条数、旅行天数与美食节次数。

第二行 n 个整数 ci，表示每座城市的美食所能提供的愉悦值。接下来 m 行每行三个整数 ui,vi,wi，依次表示每条道路的起点、终点与通行天数。

最后 k 行每行三个整数 ti,xi,yi，依次表示每次美食节的举办时间、举办城市与提供的额外愉悦值。

本题中数据保证：

对所有 1≤i≤m，有 ui=vi。但数据中可能存在路线重复的单向道路，即可能存在 1≤i<j≤m，使得ui=uj,vi=vj。
对每座城市都满足：至少存在一条以该该城市为起点的单向道路。
每次美食节的举办时间 ti 互不相同。

输出格式

输出到标准输出中。

仅一行一个整数，表示小 W 通过旅行能获得的愉悦值之和的最大值。

若小 W 无法在第 T 天回到城市 1，则输出 −1。

输入输出样例

输入 #1复制

复制代码

输出 #1复制

复制代码

输入 #2复制

复制代码

输出 #2复制

复制代码

说明/提示

样例 1 解释

该样例为题目描述中的例子，最优旅行方案见题目描述。

样例 2 解释

最优方案为 1→3→4→2→3→4→1。

第 0 天，小 W 从城市 1 开始旅行，获得愉悦值 3 并沿道路 3 通行。
第 2 天，小 W 到达城市 3，获得愉悦值 2 并沿道路 4 通行。
第 5 天，小 W 到达城市 4，由于美食节获得愉悦值 20+4 并沿道路 7 通行。
第 6 天，小 W 到达城市 2，获得愉悦值 1 并沿道路 5 通行。
第 8 天，小 W 到达城市 3，获得愉悦值 2 并沿道路 4 通行。
第 11 天，小 W 到达城市 4，获得愉悦值 4 并沿道路 8 通行。
第 16 天，小 W 到达城市 1，获得愉悦值 3 并结束旅行。
小 W 获得的愉悦值之和为 39。

样例 3

见选手目录下的 delicacy/delicacy3.in 与 delicacy/delicacy3.ans。

该样例满足 k=0

测试点约束

对于所有测试点：

1≤n≤50，n≤m≤501，0≤k≤200，1≤ti≤T≤109。

1≤wi≤5，1≤ci≤52501，1≤ui,vi,xi≤n，1≤yi≤109。

每个测试点的具体限制见下表：

测试点编号	n	m	T	特殊限制
1∼4	≤5	≤50	≤5	无
5∼8	≤50	≤50	≤52501	无
9∼10	≤50	≤50	≤109	A
11∼13	≤50	≤50	≤109	k=0
14∼15	≤50	≤50	≤109	k≤10
16∼17	≤50	≤50	≤109	无
18∼20	≤50	≤501	≤109	无

特殊限制 A：n=m 且 ui=i,vi=(imodn)+1。

附件下载

delicacy.zip1.19KB

代码实现：

复制代码

#include <bits/stdc++.h>
#define LL long long
using namespace std;

const int N = 50, M = 505, K = 205, V = 250;
const LL INF = 1ll << 60;

int L;  // 矩阵维度

// 矩阵结构体（用于转移）
struct Mat {
    LL a[V][V];
    inline void init() {  // 初始化矩阵为负无穷
        for (int i = 0; i < L; ++i)
            for (int j = 0; j < L; ++j)
                a[i][j] = -INF;
    }
};

// 向量结构体（用于状态存储）
struct Vec {
    LL a[V];
    inline void init() {  // 初始化向量为负无穷
        for (int i = 0; i < L; ++i)
            a[i] = -INF;
    }
};

// 矩阵乘法（最大值卷积）
Mat operator*(const Mat A, const Mat B) {
    static Mat T;
    T.init();
    for (int k = 0; k < L; ++k)
        for (int i = 0; i < L; ++i)
            for (int j = 0; j < L; ++j)
                T.a[i][j] = max(T.a[i][j], A.a[i][k] + B.a[k][j]);
    return T;
}

// 矩阵乘向量（状态转移）
Vec operator*(const Mat A, const Vec B) {
    static Vec T;
    T.init();
    for (int i = 0; i < L; ++i)
        for (int j = 0; j < L; ++j)
            T.a[i] = max(T.a[i], A.a[j][i] + B.a[j]);
    return T;
}

int n, m, T, k, c[N];  // n:地点数 m:边数 T:总时间 k:事件数 c:地点基础值
int ex[M], ey[M], ez[M];  // 边信息：起点 终点 权重
Mat I, Tr, A[30];  // I:单位矩阵 Tr:转移矩阵 A:矩阵幂缓存
Vec st;  // 状态向量
int nowt;  // 当前时间
int id[N][5];  // 状态编号：地点×时间阶段

// 事件结构体
struct Ev {
    int t, x, y;  // t:时间 x:地点 y:附加值
} ev[K];

int main() {
    // freopen("delicacy.in","r",stdin);
    // freopen("delicacy.out","w",stdout);
    
    int i, j;
    cin >> n >> m >> T >> k;
    I.init();
    L = n * 5;  // 维度=地点数×5（时间阶段）
    
    // 读入地点基础值
    for (i = 0; i < n; ++i)
        cin >> c[i];
    
    // 初始化单位矩阵
    for (i = 0; i < n; ++i)
        I.a[i][i] = 0;
    
    // 状态编号映射：(地点, 时间阶段) → 唯一ID
    for (i = 0; i < n; ++i)
        for (j = 0; j < 5; ++j)
            id[i][j] = j * n + i;
    
    // 读入边信息
    for (i = 1; i <= m; ++i) {
        cin >> ex[i] >> ey[i] >> ez[i];
        --ex[i];  // 转为0基
        --ey[i];
    }
    
    // 初始化转移矩阵
    Tr.init();
    // 同一地点内的时间阶段转移
    for (i = 0; i < n; ++i)
        for (j = 1; j < 5; ++j)
            Tr.a[id[i][j]][id[i][j-1]] = (j == 1) ? c[i] : 0;
    
    // 跨地点的边转移
    for (i = 1; i <= m; ++i)
        Tr.a[id[ex[i]][0]][id[ey[i]][ez[i]-1]] = (ez[i] == 1) ? c[ey[i]] : 0;
    
    // 预处理矩阵幂（二进制优化）
    A[0] = Tr;
    for (i = 1; i < 30; ++i)
        A[i] = A[i-1] * A[i-1];
    
    // 读入事件
    for (i = 1; i <= k; ++i) {
        cin >> ev[i].t >> ev[i].x >> ev[i].y;
        --ev[i].x;  // 转为0基
    }
    
    // 事件按时间排序
    for (i = 1; i <= k; ++i)
        for (j = i+1; j <= k; ++j)
            if (ev[j].t < ev[i].t)
                swap(ev[i], ev[j]);
    
    // 补充终点时间事件
    if (ev[k].t != T) {
        ++k;
        ev[k].t = T;
        ev[k].x = ev[k].y = 0;
    }
    
    // 初始状态：在起点(0号地点)，时间阶段0
    st.init();
    st.a[id[0][0]] = c[0];
    nowt = 0;
    
    // 处理每个事件段
    for (i = 1; i <= k; ++i) {
        int dt = ev[i].t - nowt;  // 时间差
        // 用二进制幂加速转移
        for (j = 0; j < 30; ++j)
            if (dt >> j & 1)
                st = A[j] * st;
        
        // 累加事件附加值
        if (st.a[ev[i].x] >= 0)
            st.a[ev[i].x] += ev[i].y;
        
        nowt = ev[i].t;
    }
    
    // 输出结果（若不可达输出-1）
    cout << (st.a[0] < 0 ? -1 : st.a[0]) << '\n';
    return 0;
}