文章目录
- 思维
-
- [Round 1019(div2) C - Median Splits(中位数)](#Round 1019(div2) C - Median Splits(中位数))
- [Round 1008 (Div. 2) CBreach of Faith](#Round 1008 (Div. 2) CBreach of Faith)
- [Round 1007 (Div. 2) C. Trapmigiano Reggiano](#Round 1007 (Div. 2) C. Trapmigiano Reggiano)
- 树上问题
-
- [1.CF1328E Tree Queries(树上问题)](#1.CF1328E Tree Queries(树上问题))
- 2.2025牛客暑期多校训练营3H
- 数据结构优化
- 组合数
- 括号匹配问题
-
- [2025牛客暑期多校训练营4 G](#2025牛客暑期多校训练营4 G)
思维
Round 1019(div2) C - Median Splits(中位数)
中位数常见套路,维护前缀和, a i ≥ x a_i\ge x ai≥x 设置为1 ,小于 x 设置为 -1 。若存在子数组大于等于0,则说明最大中位数一定大于等于 x 。
题意:把数组分成三段,使得三段的中位数组成的数组的中位数小于等于 k k k。
记录 s u m i sum_i sumi为前 i i i个小于等于 k k k的个数。然后把满足中位数小于等于 k k k的前缀和后缀存下来。
如果最前的前缀和最后的后缀中间至少有一个数,就满足条件了。
否则如果前缀个数或后缀个数大于2也满足条件。再否则讨论两个前缀和两个后缀的情况,如果两个前缀之间中位数小于等于k也满足,后缀同理讨论。
我们遇到求中位数的时候可以做前缀或后缀和存储 <=m 的数的个数
Round 1008 (Div. 2) CBreach of Faith

b i ≤ 1 e 9 b_i \le 1e9 bi≤1e9 奇数位置 n+1 个,偶数 n 个,将前 n+1 大值给奇数, n-1 小的给偶数,构造出来的第 n 个偶数一定是 > m x >mx >mx。
Round 1007 (Div. 2) C. Trapmigiano Reggiano
原题大意:给定一棵 n 个节点的树,并给出两个节点 s t , e n st,en st,en,求一个从 1 到 n 的排列,使得初始时从 st 出发,第 i i i 步朝排列中 p i p_i pi 结点移动一步,使得最终移动完 n 步后恰好能停在 en 点上。
做法:这个题首先思考,如果朝着离 en 最远的点走,那么最远会走到某个最远的点,接下来,朝着所有次远点走,则最远走到某个次远点,以此类推,当我们按距离 en 距离的降序顺序走完第 x 层点,那么此时最远应停在与 en 距离 x 远的点上,所以如果我们按照这个顺序走,最终会停在距离 en 点长度为 0 的点上,也就是 en 点。
树上问题
1.CF1328E Tree Queries(树上问题)
https://www.luogu.com.cn/problem/CF1328E
给定一棵有 n n n 个顶点的有根树,顶点编号为 1 1 1 到 n n n,树的根为顶点 1 1 1。
树是一个连通无向图,包含 n − 1 n-1 n−1 条边。
你需要回答 m m m 个询问。第 i i i 个询问给出一个包含 k i k_i ki 个不同顶点的集合 v i [ 1 ] , v i [ 2 ] , ... , v i [ k i ] v_i[1], v_i[2], \dots, v_i[k_i] vi[1],vi[2],...,vi[ki]。你的任务是判断是否存在一条从根到某个顶点 u u u 的路径,使得给定的 k k k 个顶点中的每一个,要么在这条路径上,要么与这条路径上的某个顶点的距离为 1 1 1。
2 ≤ n ≤ 2 ⋅ 10 5 2 \le n \le 2 \cdot 10^5 2≤n≤2⋅105, 1 ≤ m ≤ 2 ⋅ 10 5 1 \le m \le 2 \cdot 10^5 1≤m≤2⋅105
题目难点转化:
可以把 "是否有一条以根节点为一端的链使得询问的每个节点到此链的距离均 ≤1 " 中的每个节点换成它的父亲,那么题意就转化为 "是否有一条以根节点为一端的链使得询问的每个节点在链上" 。
对于一些在同一条一端为根的链上的点,显然深度小的点是深度大的点的祖先。
于是只要对每次询问的几个点取个父亲,在根据深度排个序,相邻的两个验证一下是否有祖先与子孙的关系就好了。
cpp
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
vector<int> g[N];
int fa[N], dep[N], son[N], top[N], siz[N];
int id[N], nw[N], cnt;
int w[N], n, m, root, p;
void dfs1(int u, int father) {
dep[u] = dep[father] + 1, fa[u] = father, siz[u] = 1;
for (auto v : g[u]) {
if (v == father)
continue;
dfs1(v, u);
siz[u] += siz[v];
if (siz[son[u]] < siz[v])
son[u] = v;
}
}
void dfs2(int u, int t) {
top[u] = t, id[u] = ++cnt, nw[cnt] = w[u]; // 记录链头
if (!son[u])
return; // 无重儿子返回
dfs2(son[u], t); // 搜重儿子
for (auto v : g[u]) {
if (v == fa[u] || v == son[u])
continue;
dfs2(v, v); // 搜轻儿子
}
}
int lca(int u, int v) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]])
swap(u, v);
u = fa[top[u]];
}
return (dep[u] < dep[v]) ? u : v;
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
for (int i = 1; i <= n - 1; i++) {
int u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
dfs1(1, 0);
dfs2(1, 1);
while (m--) {
int k;
cin >> k;
vector<int> a(k + 1);
for (int i = 1; i <= k; i++) {
int x;
cin >> x;
if (x == 1)
a[i] = 1;
else
a[i] = fa[x];
}
sort(a.begin() + 1, a.end(), [&](const int x, const int y)
{ return dep[x] < dep[y]; });
bool flag = true;
for (int i = k; i >= 2; i--) {
if (lca(a[i], a[i - 1]) != a[i - 1]) {
flag = false;
break;
}
}
if (flag)
cout << "YES" << '\n';
else
cout << "NO" << '\n';
}
return 0;
}2.2025牛客暑期多校训练营3H
给定一棵 n n n 个结点的树。有一枚棋子初始位于1号结点。
按序给定 k k k 个时间段。第i个时间段 [ l i , r i ] [l_i,r_i] [li,ri]中,树上会出现一个目标 u i u_i ui。
保证时间段两两不交。
每一时刻,若目标存在,棋子与目标位置不同且连通,则棋子向目标移动一步;否则棋子不动。若此时二者位置相同,则称该时刻二者重合。
你可以在任意时刻切断树上任意数量的边。每条边被切断后不会恢复。
判断棋子能否与目标重合,若能则最小化重合发生的时刻。
1 ≤ n ≤ 10 6 , 1 ≤ k ≤ 10 6 , 1 ≤ u i ≤ n , 1 ≤ l i ≤ r i ≤ 10 9 1 ≤n≤10^6,1≤k≤10^6,1≤u_i ≤n,1≤l_i ≤r_i ≤10^9 1≤n≤106,1≤k≤106,1≤ui≤n,1≤li≤ri≤109。
题解:
观察到任意时刻可达的点是一个包含根的极大连通块。
考虑直接维护这个连通块,当目标在 [ l i , r i ] [l_i,r_i] [li,ri] 时刻内出现在 u i u_i ui 时,相当于将这个连通块向ui 方向扩张 ( r i − l i + 1 ) (r_i−l_i+1) (ri−li+1) 步。
考虑使用倍增,从 u i u_i ui 开始向上找到最接近的可达点,然后暴力向下逐步标记为可达,若在 ( r i − l i + 1 ) (r_i−l_i+1) (ri−li+1) 步前 u i u_i ui 已经被标记可达即可输出答案。
时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)
该题可以转化为:一颗有根树上,从某个结点跳到距离根最近的未到达结点,可以用倍增法往上跳。
cpp
int n,k;
cin>>n>>k;
vector<vector<int>> fa(n+1,vector<int>(30));
for(int i=2;i<=n;i++){
int f;cin>>f;
fa[i][0]=f;
}
for(int j=1;j<20;j++){
for(int i=1;i<=n;i++){
fa[i][j]=fa[fa[i][j-1]][j-1];
}
}
vector<int> vis(n+1);
vis[1]=1;
int u,l,r;
for(int i=1;i<=k;i++){
cin>>u>>l>>r;
for(int t =l;t<=r;t++){
int x =u;
for(int j=19;j>=0;j--){
if(!fa[x][j]||vis[fa[x][j]])continue;
x=fa[x][j];
}
if(x==u){
cout<<t<<"\n";
return ;
}
vis[x]=1;
}
}
cout<<-1<<"\n";数据结构优化
线段树

翻转后的样子要么是010101...,要么就是101010...。
我们用线段树维护01开头和10开头所需要的最小翻转次数。
并查集加速
我们面对要进行大量区间遍历且只要区间内满足某些条件的时候我们就不再遍历。这个时候我们可以用并查集来进行区间优化,可以直接跳到下一个不满足条件的区间,这样就可以进行时间复杂度的优化,具体来说可以看下面的代码
cpp
for(int j=l;j<=r;j=find(j)+1){
if(!vis[j]){
rnk[++now]=j;
vis[j]=now;
p[j-1]=j;
}
}组合数
2025牛客暑期多校训练营6C


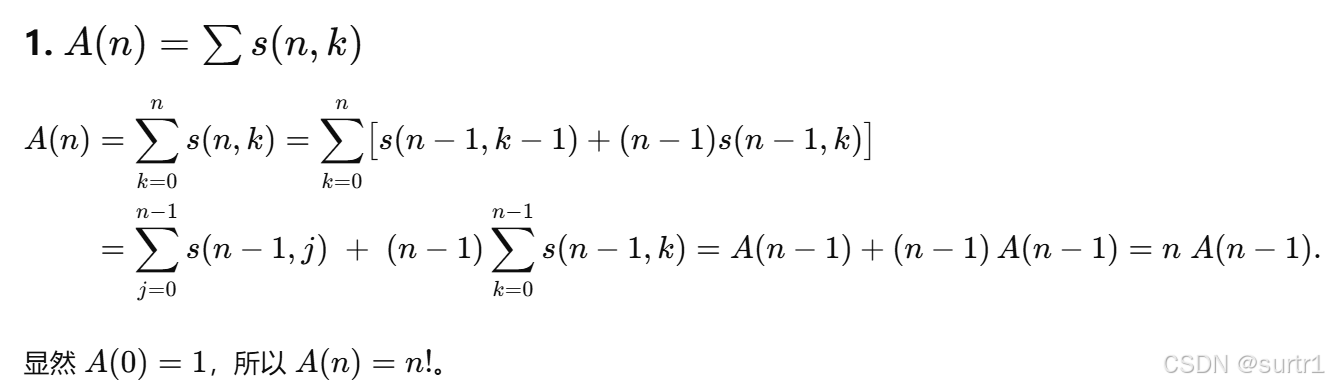

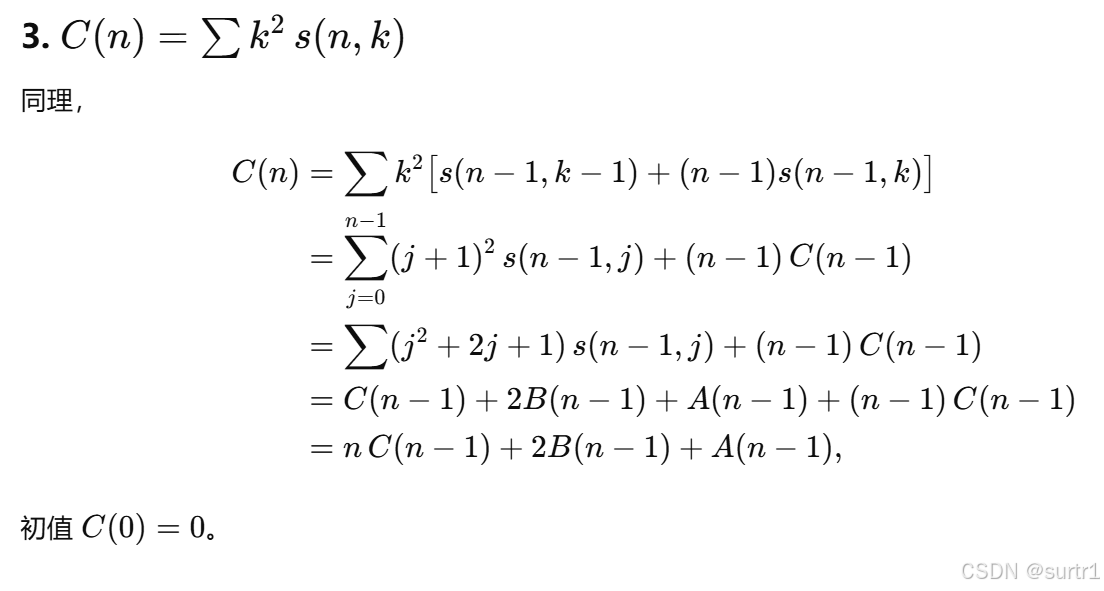
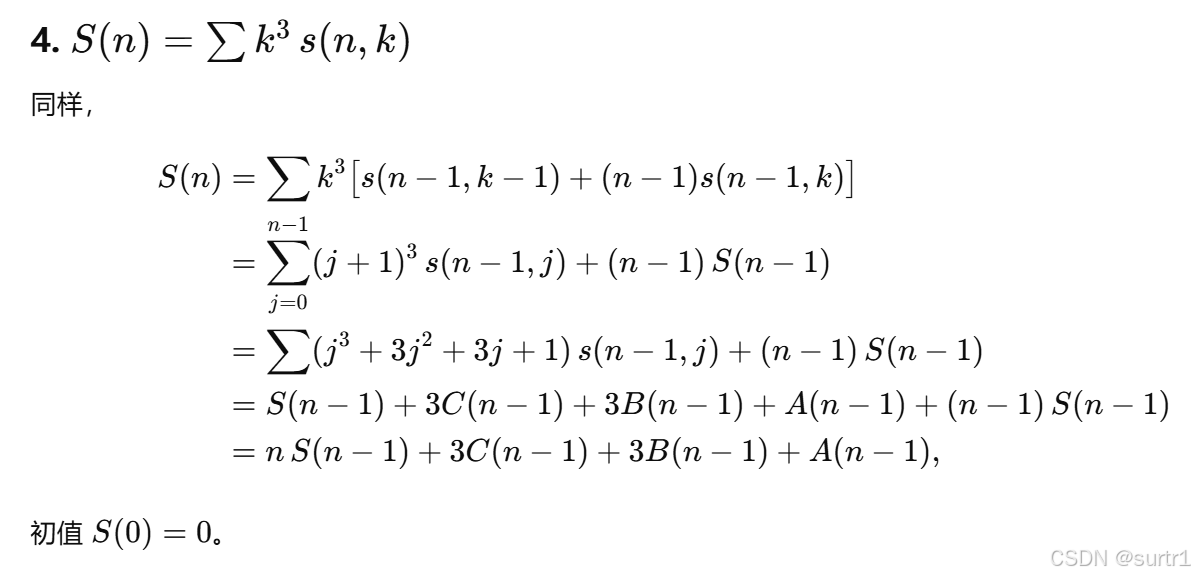
括号匹配问题
2025牛客暑期多校训练营4 G

我们考虑两个括号 s i = ′ ( ′ , s j = ′ ) ′ s_i='( ' , s_j=') ' si=′(′,sj=′)′
如果 i > j i>j i>j 不管怎么样,两个位置对调后括号序列还是合法的。
如果 i < j i<j i<j 我们定义括号序列 ′ ( ′ '(' ′(′ 为 + 1 +1 +1, ′ ) ′ ')' ′)′ 为 − 1 -1 −1,做一次前缀和
序列合法当且仅当 对于任意 i , f [ i ] ≥ 0 , 且 f [ n ] = 0 i ,f[i] \ge 0,且f[n]=0 i,f[i]≥0,且f[n]=0。
交换 s [ i ] , s [ j ] , f [ n ] s[i],s[j],f[n] s[i],s[j],f[n]不变,但是对于 k ∈ [ i , j − 1 ] , f [ k ] − = 2 k\in [i,j-1],f[k]-=2 k∈[i,j−1],f[k]−=2
所以当且仅当 k ∈ [ i , j − 1 ] , f [ k ] ≥ 2 k\in [i,j-1],f[k]\ge 2 k∈[i,j−1],f[k]≥2 交换后才合法
对于一个操作序列 ,有若干个 ′ ( ′ '(' ′(′ 和 ′ ) ′ ')' ′)′。
序列唯一确定当且仅当:对任意 i , j , s i = ′ ( ′ , s j = ′ ) ′ i,j,s_i= '(' ,s_j=')' i,j,si=′(′,sj=′)′,只要 s i , s j s_i,s_j si,sj交换,序列就都不合法
我们如何计数呢?对于每一个左括号 i i i,计算出来他所能衍生到的最大的可以做交换操作右括号下标 r [ i ] r[i] r[i]。
枚举最后一个模糊位置的左括号,当且仅当 下标在 r [ i ] r[i] r[i] 前的右括号不模糊且 i + 1 i + 1 i+1 后的左括号不模糊
注意左括号全不模糊的情况也是合法的。
cpp
const int N = 5e5 + 10;
ll inv2 = (mod + 1) / 2;
void Main() {
vector<ll> p2(N + 1);
p2[0] = 1;
for (int i = 1; i <= N; i++) {
p2[i] = (p2[i - 1] * inv2) % mod;
}
string s;
cin >> s;
int n = s.size();
s = " " + s;
vector<int> f(n + 1);
vector<int> lf(n + 1), rg(n + 1);
for (int i = 1; i <= n; i++) {
lf[i] = lf[i - 1] + (s[i] == '(');
rg[i] = rg[i - 1] + (s[i] == ')');
f[i] = f[i - 1] + (s[i] == '(' ? 1 : -1);
}
vector<int> r(n + 1);
for (int i = 1; i <= n; i++) {
int j = i;
if (s[i] == '(') {
if (f[i] < 2) {
r[i] = i;
continue;
}
while (j + 1 <= n && f[j + 1] >= 2) j++;
for (; i <= j; i++)
if (s[i] == '(')
r[i] = j + 1;
i = j;
}
}
// 左括号全不模糊
ll ans = p2[n / 2];
for (int i = 1; i <= n; i++) {
if (s[i] == '(') {
// 右边的左括号不模糊
// 注意i本身是模糊的
ll pl = p2[n / 2 - lf[i] + 1];
// r[i]及前面的右括号不模糊
ll pr = p2[rg[r[i]]];
ans = (ans + pl * pr % mod) % mod;
}
}
cout << ans << "\n";
}