前言
在二叉树问题中会有许多许多问题通过递归的方式进行,有些问题经常会特别的绕,这次我选择了十几个题进行代码演示,思想推理,逐步调试,简图注解,梳理递归的基本思想.
让我们开始吧~~
一、判断对称二叉树
题目解释
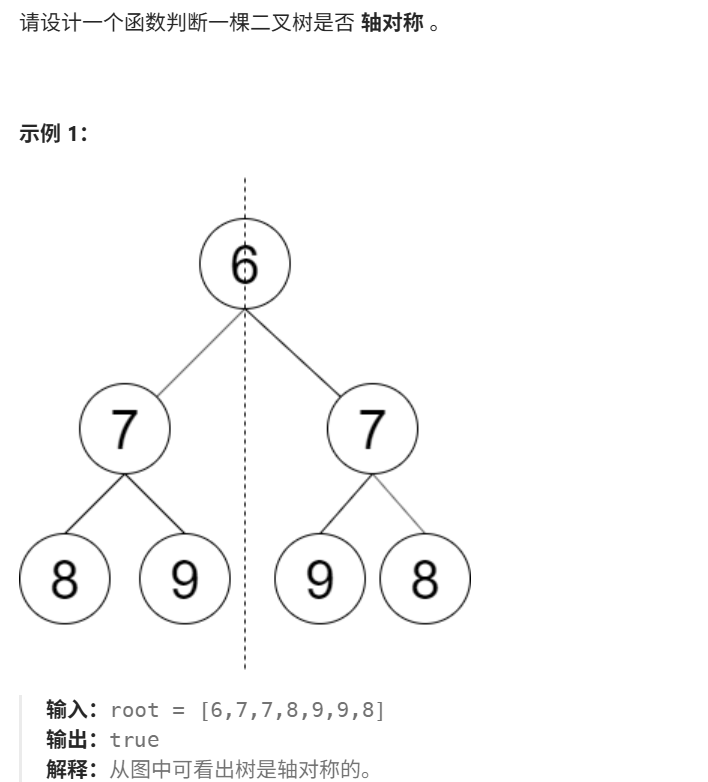
- 形如下图的二叉树,这里就是中学阶段的轴对称概念,应该是比较好理解的
- 当碰到二叉树递归问题,要有的总的思想就是子问题思考,从头结点带入,当满足其他条件时候进入下一个子树,将子树当成一个新的树进行处理.
代码演示
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean checkSymmetricTree(TreeNode root) {
//首先进入根节点
if (root == null){
return true;
}
return isSymmetricChild(root.left,root.right);
}
public boolean isSymmetricChild(TreeNode lRoot,TreeNode rRoot){
//一个为空,另一个不为空
if ((lRoot == null && rRoot != null)
|| (lRoot != null && rRoot == null ) ) {
return false;
}
//两个都为空
if (rRoot == null && lRoot == null){
return true;
}
//两个子树值不相等
if (rRoot.val != lRoot.val){
return false;
}
//剩下的就是两个子树的值相等,需要进行下一步判断
return isSymmetricChild(lRoot.left,rRoot.right)
&& isSymmetricChild(lRoot.right,rRoot.left);
}
}思想推理
1.进入根节点,无非就是null与!null,当root = null ,我们认为是轴对称树.
2.接下来就是要对子树进行判断,我们用一个函数来进行代替,进入子程序能够想到的几种情况
1.两个根节点一个为空一个不为空
2.两个节点都是空
3.两个不空,但是值不是一样的
4.两个值非空,且是一样的
3.到这里我们想直接返回true吗?,回想从根节点到子节点我们也没有直接返回,而是继续向下判断.这里也是一样,来递归我们这个树,下一次比较的是**左边的左与右边的右,左边的右与右边的左.**这个大家自己画一下就能清楚地明白.
4.这里有的同学会有疑问到了第三层,和后面更深的树是怎么遍历的,值是怎一步一步返回的,我们呢在环境中进行调试来看一下~
代码调试
我们按下图片的题目进行调试
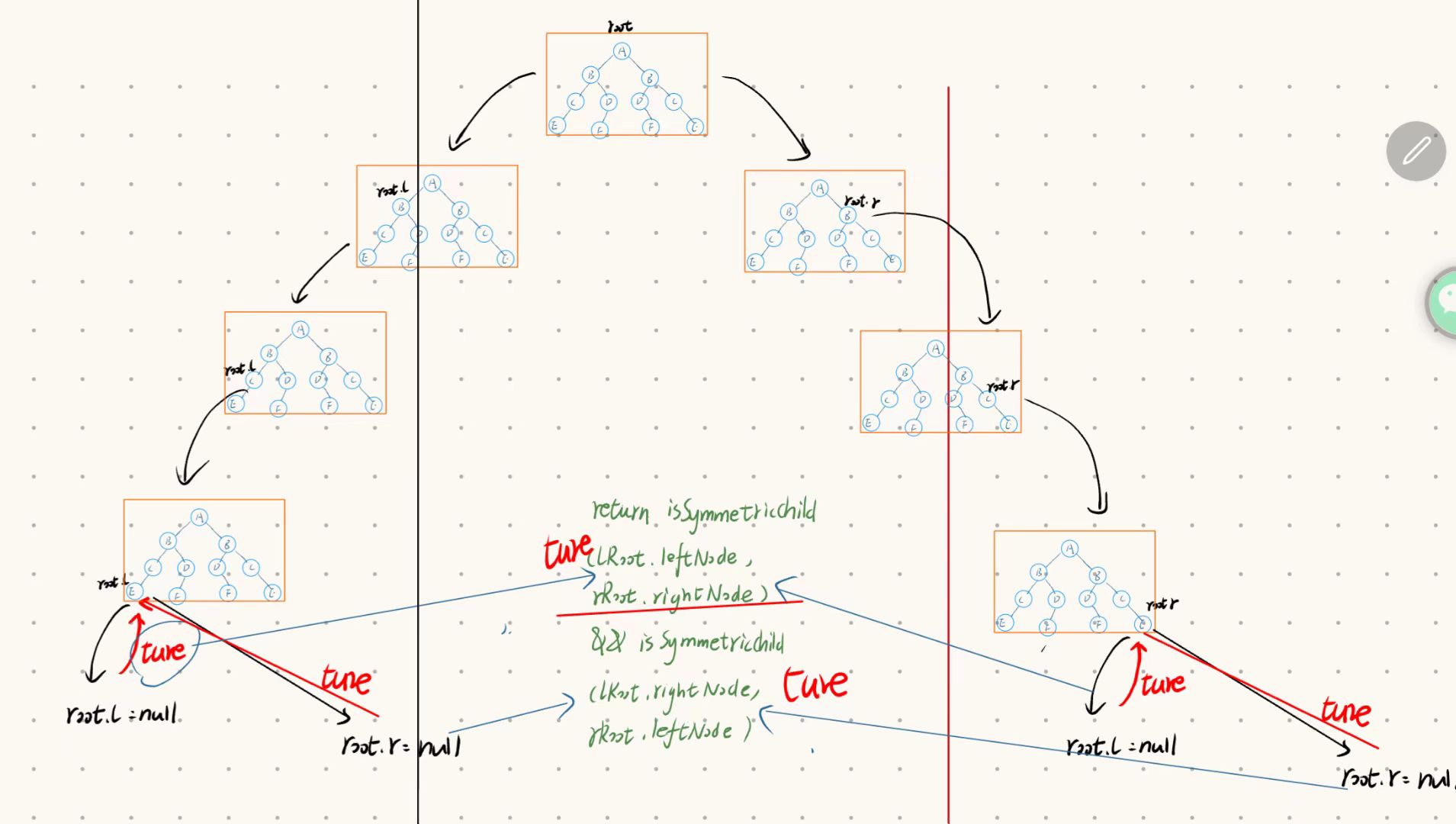
- 因为计算机调试不容易讲解,我使用手绘方式进行调试遍历.但是还是推荐大家上手调试~~
- 这就像是从根节点出发分为两个路进行递归,
1.比如到达E,E2时候判断,e.l = e2.r = null 返回true. e.r = e.l = null - 返回true true&&true --->return true给到上一层
isSymmetricChild(lRoot.leftNode,rRoot.rightNode)是真的,在进行下一部分&& isSymmetricChild(lRoot.rightNode,rRoot.leftNode),我们知道都是null,返回当然为true.这时候两个部分都为true 自然会返回true true&&true --->return true给到上一层.
反复进行,直到返回根节点. - 总的感觉就是从两边进行跑,直到返回~~
二、平衡二叉树
题目解释
- 值得注意的是,左右子树不超过高度差不超过1,是每个节点的左右子树都要遵循.

代码演示
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isBalanced(TreeNode root) {
if(root == null){
return true;
}
//把左边的子树看成一个新树,得到他的高度
int leftH = getH(root.left);
int rightH = getH(root.right);
//只是满足了第二层的标准,也就是说第二层满足二叉树
//的条件,而下面还存在着很多子树
return Math.abs(leftH - rightH) <= 1
&& isBalanced(root.left)
&& isBalanced(root.right);
}
public int getH(TreeNode root) {
if (root == null) {
return 0;
}
int leftH = getH(root.left);
int rightH = getH(root.right);
//最后返回的是两个子树
return Math.max(leftH, rightH) + 1;
}
}思想推理
首先我们总的思路还是从根节点进行出发思考
1.root == null 我们也认为这满足平衡二叉树的概念
2.平衡二叉树的概念就是每个节点的子树之差不得超过1,是每个节点,我们还是从的第一个节点的左右出发,我们想要计算每个节点左右子树只差需要完成一个求高度的方法,getH方法.
3.有了getH就可以判断前这一层是不是平衡二叉树了
4.但是还没完,我们是需要每一个子树都要满足
- getH方法.总体的思路就是先找到最深的根,
1.当root = = null时候返回0,我们就像都返回0了怎么计算长度,这只是左右树的其中一个,当两个都返回时,我们就手动+1.来记录这一个节点,也就是高度
2.那么对不是最深的根,那就会有左面,右面较为长的一个,这时候我们就会拿到较为深的那一个,然后在+1.
3.一直进行返回高度,这时候就要继续递归判断左树,右树是否满足,直到每个节点都是满足的.
代码调试
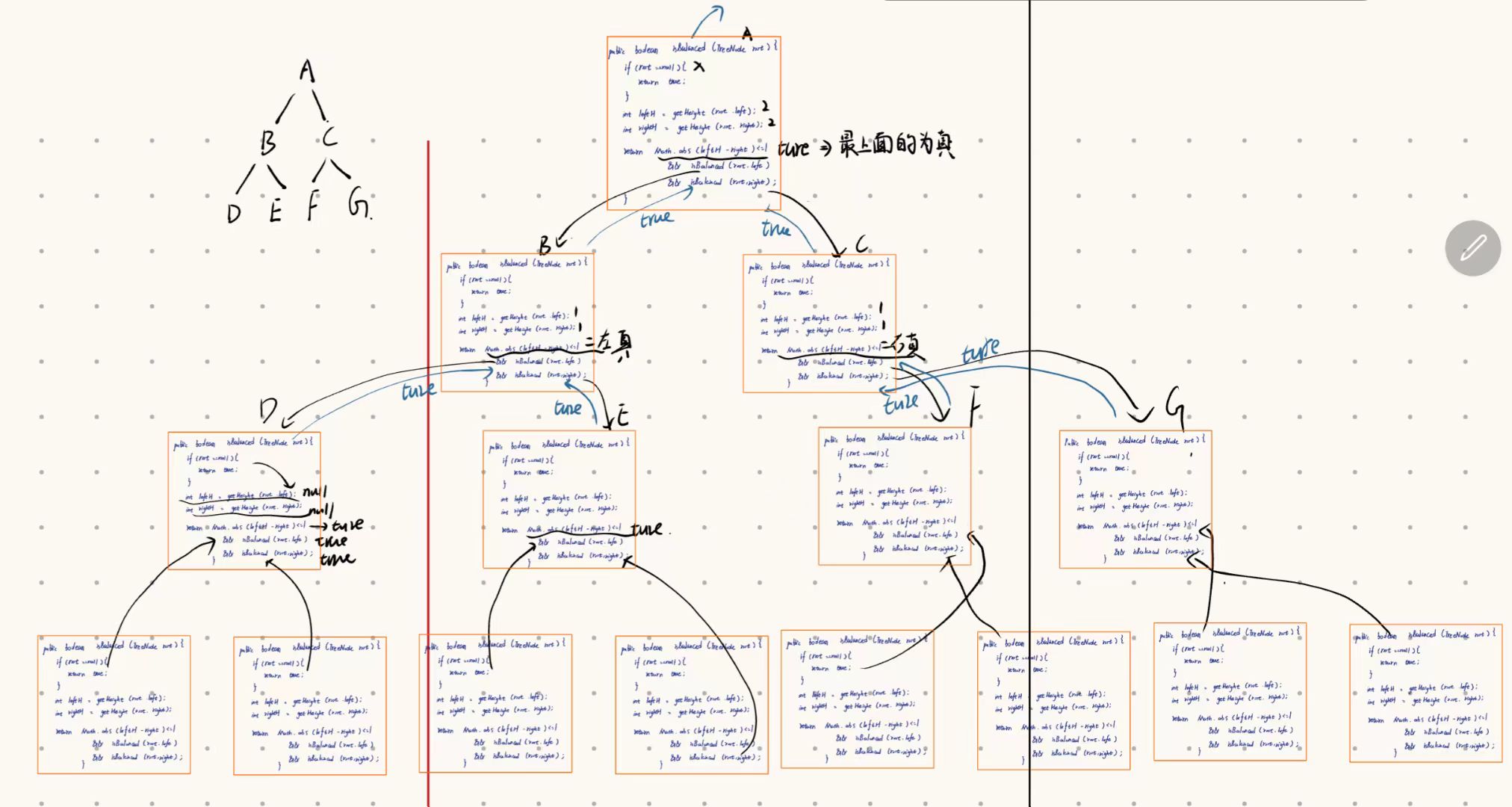
三、前序字符串进行树的前序构建
题目解释
- 简单说就是给一组字符串,通过前序遍历的方式进行构建.
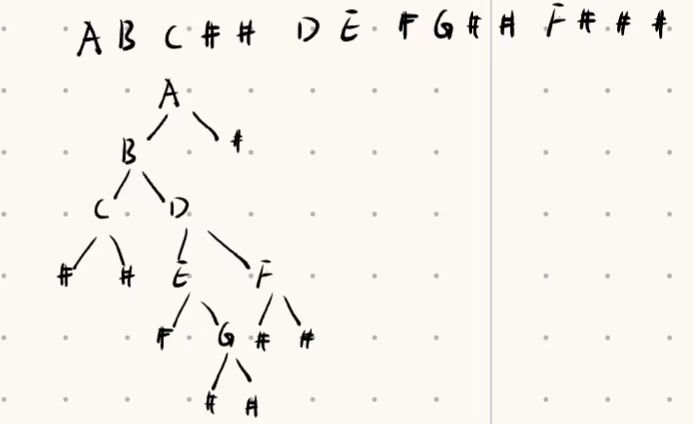
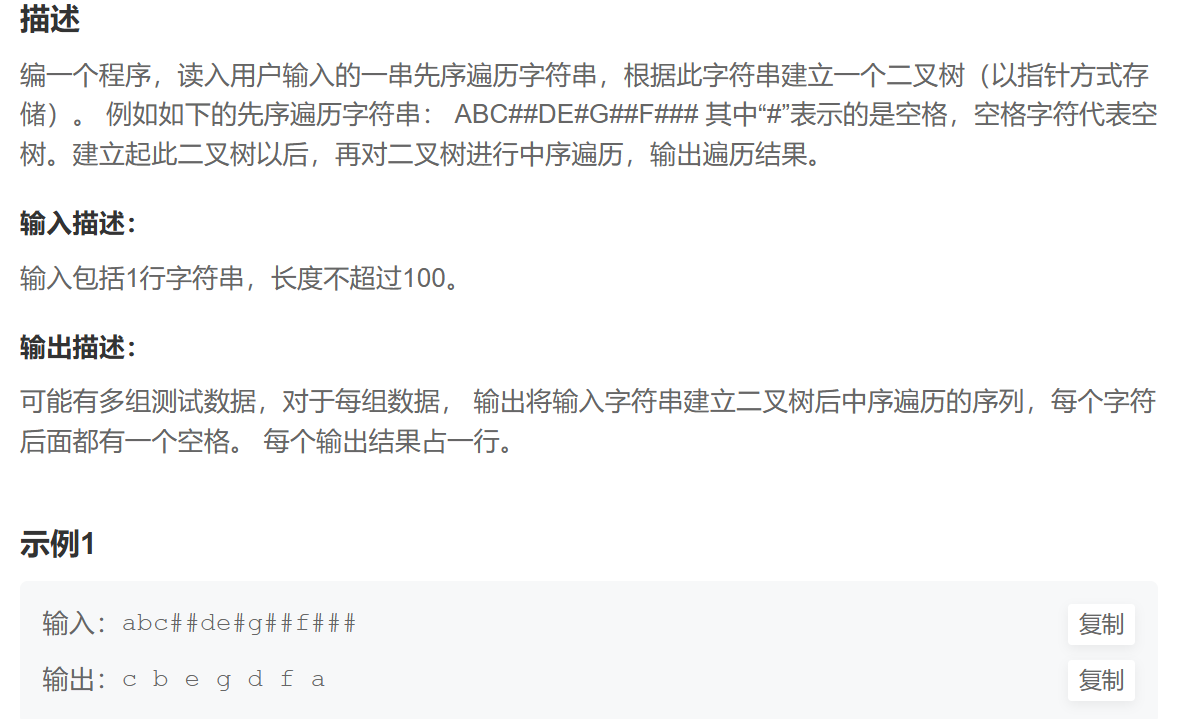
代码演示
java
import java.util.Scanner;
class TreeNode {
public char val;
public TreeNode left;
public TreeNode right;
public TreeNode (char val) {
this.val = val;
}
}
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static int i = 0;
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 注意 hasNext 和 hasNextLine 的区别
while (in.hasNextLine()) { // 注意 while 处理多个 case
String str = in.nextLine();
TreeNode root = createTree(str);
inorder(root);
}
}
public static TreeNode createTree(String str) {
// int i = 0;
char ch = str.charAt(i);
//定义一个根节点
TreeNode root = null;
if (ch != '#') {
//将第一个数值放在root节点
root = new TreeNode(ch);
i++;
//第一个成功,继续构造下面的子树
root.left = createTree(str);
root.right = createTree(str);
} else {
i++;
}
return root;
}
public static void inorder(TreeNode root) {
if (root == null) {
return ;
}
inorder(root.left);
System.out.print(root.val + " ");
inorder(root.right);
}
}思想推理
这一题总的思路就提取字符串中的每一个元素进行创建链接成为一个树,在经过前序遍历将这个树遍历出来,那么关键就是创建这个方法.
1.我们通过遍历将每一个字符从字符串中拿出来后,我们直接的一个思路就是判断他是不是#号,
2.是,我们就new一个新的TreeNode存放这个节点数据,并且让i++以便于拿到下一个节点数据.
3.好了我们的第一层数据已经拿到了,需要创建第二层的数据,使用我们递归的思想,下一个节点和上面的条件是相同,
4.如果是# ,也就是null的意思,我们直接i++,进行下一个元素的判断
到这里你可能存在一个疑问就是,你都是在创建节点,并没有进行节点之间的链接,怎么能够创建成为一颗树呢?在下面的代码调试中你会发现在返回的时候已经开始从底部一点一点的进行链接了~
代码调试
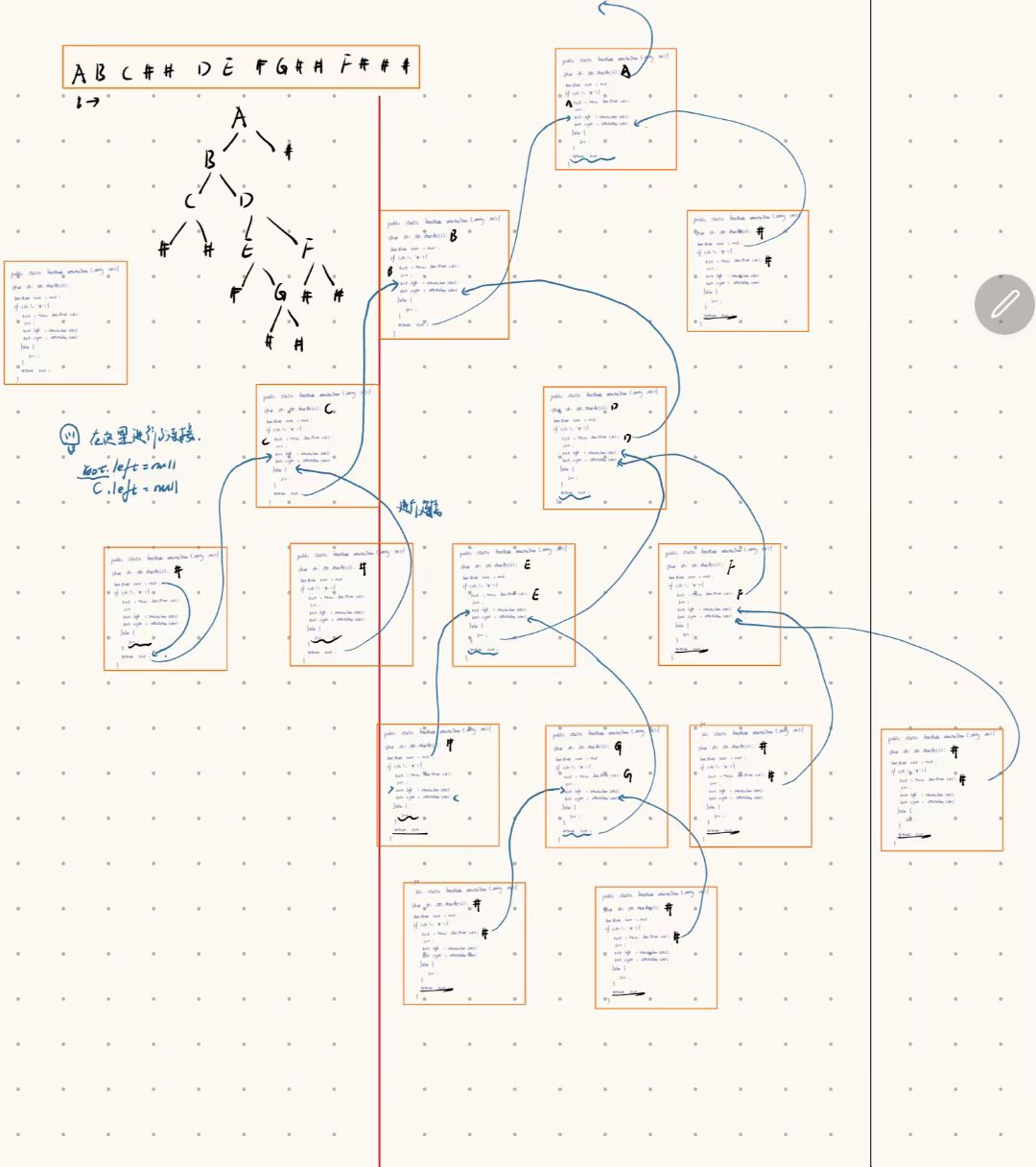
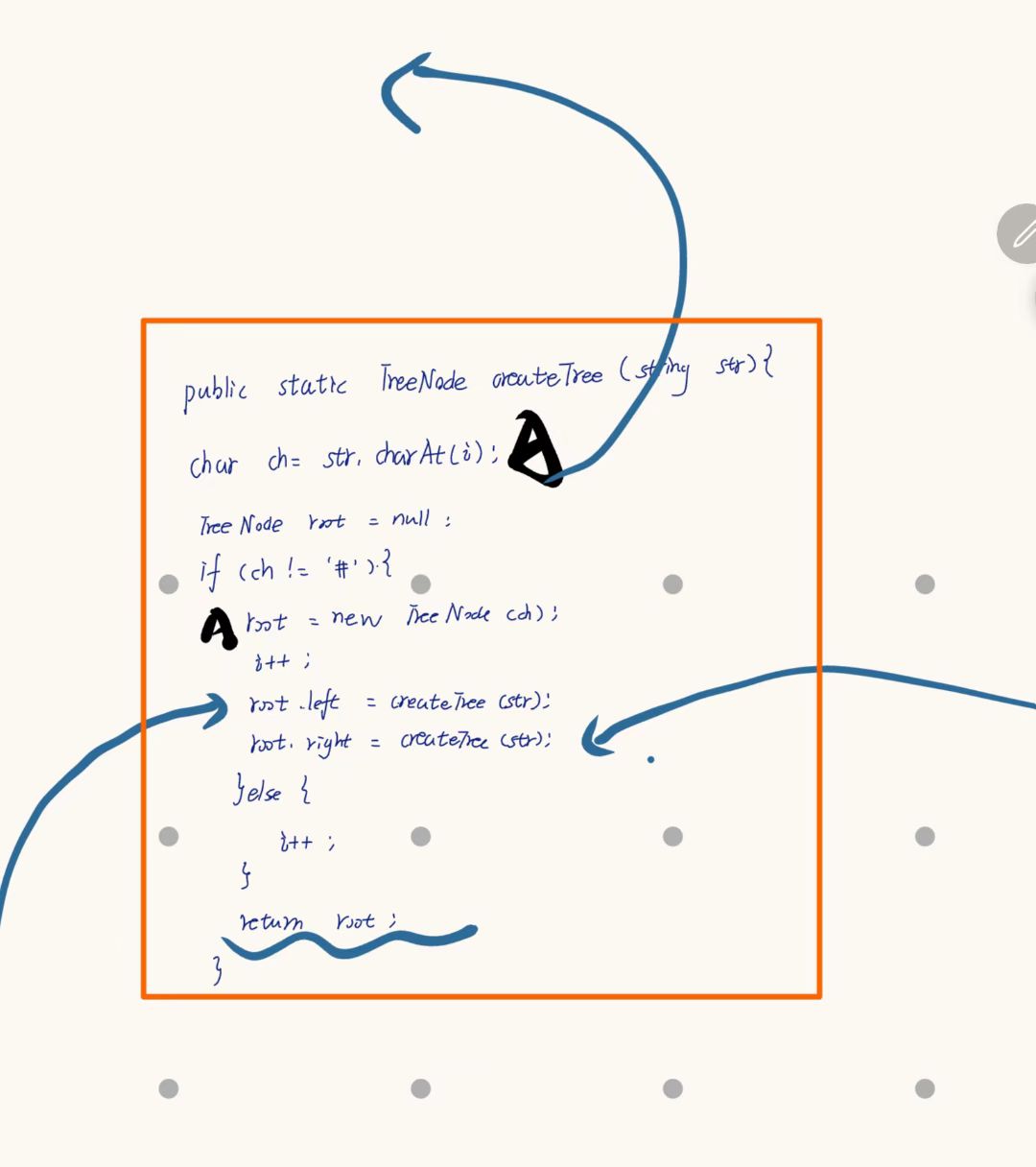
在上面可以看到,因为我们在创建的过程中新的子树接受的就是root ,在这个时刻,树就完成的链接~
四.二叉树的层序遍历
题目解释
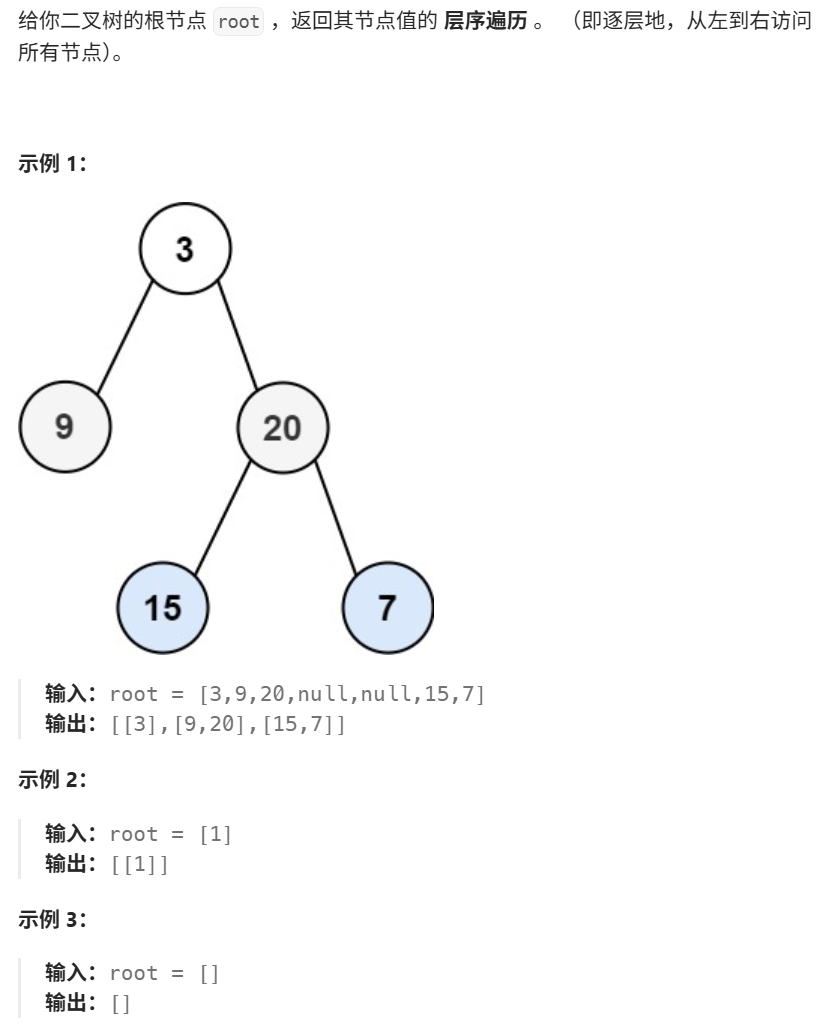
题目的意思也是比较简单,就是将一个二叉树一层一层的遍历一下.
代码演示
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> ret = new ArrayList<>();
if(root == null){
return ret;
}
//创建一个队列
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);//A
//创建一个列表
while(!queue.isEmpty()){
List<Integer> curRow = new ArrayList<>();
int size = queue.size();
while (size != 0){
//当存入的节点不是0,出这个元素放在队列里面,添加子节点.
TreeNode cur = queue.poll();
curRow.add(cur.val);
if(cur.left != null){
queue.offer (cur.left);
}
if(cur.right != null){
queue.offer(cur.right);
}
size--;
}
ret.add(curRow);
}
return ret;
}
}思想推理
这和题目需要的是用二维链表进行呈现.这次我们需要借助队列进行完成.
首先创建一个新的二维队列ret,我们之后的每一层就是要放在这里面的.创建一个普通的链表,来存放每一层的具体元素.
1.当我的树是空树的时候,直接返回我们的ret即可.此时的ret是空链表,也就是空的.
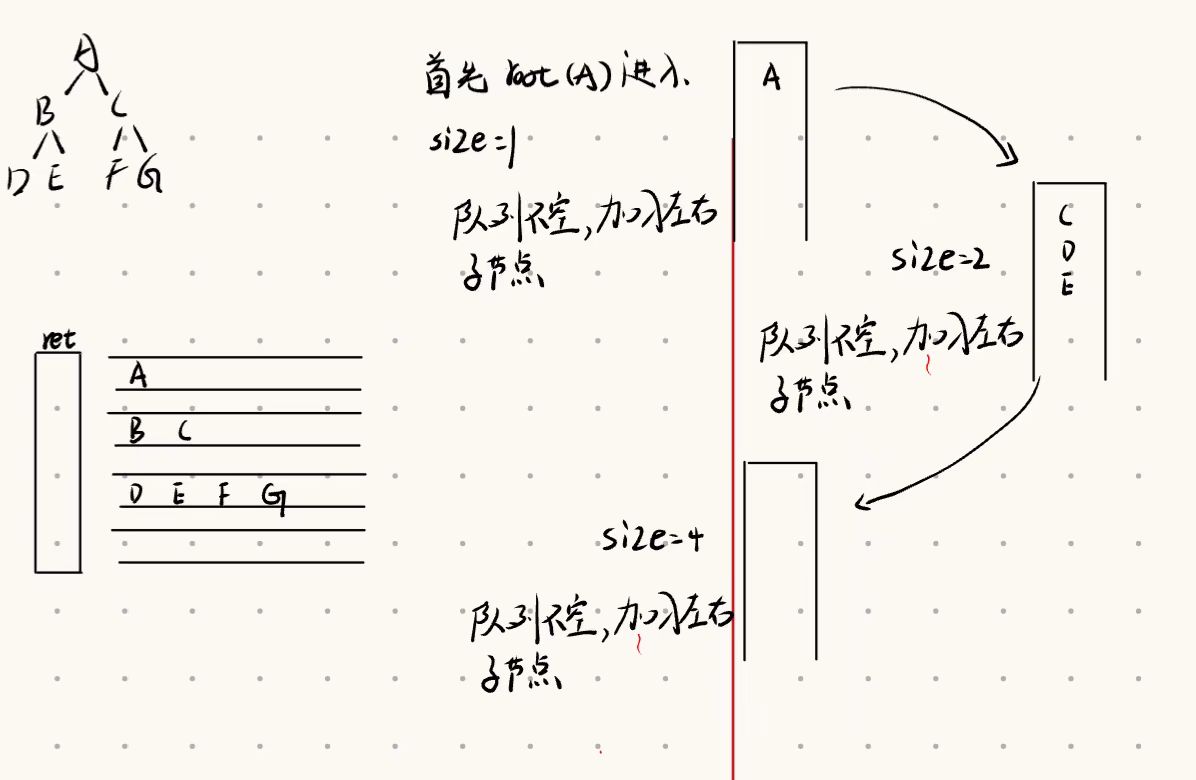
2.当不为空的时候.根节点是单独的一层,我们直接offer(root).也就是放在我们的第一个链表中.算是一层.
3.当我们进入第二层时候,我们该如何确定当层有多少个节点进行? 我们先来看一下直接遍历每一层的节点数,
从第二层开始,我们放入一个root,此时队列不为空,创建一个临时的队列存放这一层的数据,
4.此时队列里面不是空,我们就poll出去,并把它放在临时链表中,向队列中放入root的左右节点,如此反复,出一个,就会将他的左右节点中心放入里面.怎样记录每一层的,我们可一看到,当队列中的个数为1是,出1.为2时候,我让他出2,4出4.哪里这里的1,2,4,8当如何确定就是定义一个size,当size=1,加入两个新的.
size = 2 .加入4个
size = 4 加入8个
最后返回带一维链表,再返回二维链表.
代码调试
在这个代码中比较重要的是明白在入队列,出队列问题,特别巧妙的更是size的大小与新增元素的准确性.
五、判断完全二叉树
题目解释
判断一个树是不是完全二叉树
- 结构定义:除了最后一层外,其他层的节点都被完全填满;最后一层的节点从左到右依次排列,没有空缺。
代码演示
java
import java.util.LinkedList;
import java.util.Queue;
public class MyTree {
//定义静态内部类型
static class TreeNode {
public char val;
public TreeNode right;
public TreeNode left;
//再类中实现构造方法
public TreeNode(char ch) {
this.val = val;
}
}
public boolean isCompleteTree(TreeNode root) {
if (root == null) {
return true;
}
//创建队列
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root); //A
while (!queue.isEmpty()) {
TreeNode cur = queue.poll();
if (cur != null) {
queue.offer(cur.left);
queue.offer(cur.right);
} else {
break;
}
}
//判断队列中剩余的元素是不是都是空
while (!queue.isEmpty()) {
TreeNode cur = queue.peek();
if (cur != null) {
return false;
} else {
queue.poll();
}
}
return true;
}
}思想推理
1.首先使用层序遍历的思想将每个元素放在队列中.头节点一定先放在队列中
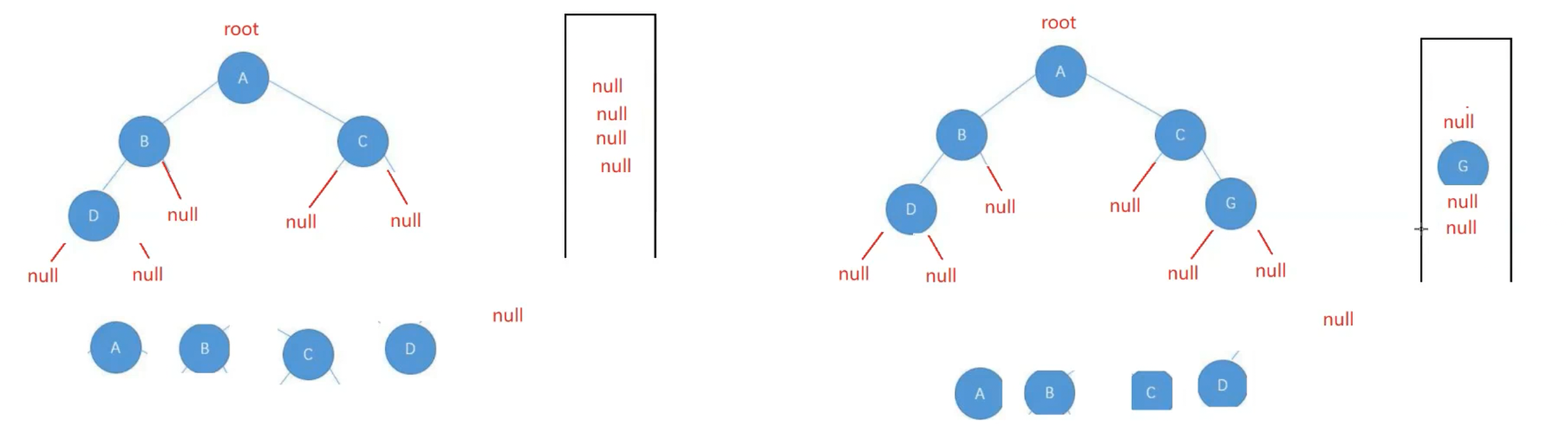
2.如果队列不是空,将头节点放出,队列里面放入左右两个子节点,在判断是不是空,在放入.显然如果是完全二叉树最后队列中是没有实际元素的.
3.如果我出队列是一个null,理论上就是队列中全部是null,也就是空队列.这就是完全二叉树.这时候我就要检查队列里面的元素,如果不都是null 他就不是完全二叉树.
代码调试
这里没有递归的涉及主要是整体的一个思想.下买呢我给一个简图表述不同的两种情况.
总结
好啦~ 我们上半部分的题目就分享到这里了.
谢谢大家的阅读。如有问题请直接指出。
- 我是Dylan,下次见~